某些双曲方程组关于η(uε)t+q(uε)x的H-1紧性
陈 羿,郝 鹏,陆云光
(杭州师范大学理学院,浙江 杭州 310036)
1 正 文
在以下定理中,Murat给出了证明η(uε)t+q(uε)x的H-1紧性的标准方法.

证明过程见参考文献[2].
下面来看如何利用上述的定理证明标量方程关于η(uε)t+q(uε)x的H-1紧性.首先,在标量方程的右端加上黏性项
ut+f(u)x=εuxx,
(1)
存在有界可测初值
u(x,0)=u0(x),
(2)
对每个固定的ε,因为初值在L∞空间中有界,则由抛物型方程的极值原理知,黏性解uε有先验L∞估计:
||uε(x,t)||L∞≤||u0(x)||L∞,
(3)
这表明了t>0时,uε的存在性,见参考文献[2].

(4)
因而,

(5)
对任意熵η∈C2,由方程(1)可得
(6)
其中,q是相应于熵η的熵流.

对于非线性双曲方程组
ut+f(u,v)x=0,vt+g(u,v)x=0,
(7)
我们同样在方程组(7)的右端添加黏性项,接着研究抛物型方程组
ut+f(u,v)x=εuxx,vt+g(u,v)x=εvxx,
(8)
存在有界可测初值
(u(x,0),v(x,0))=(u0(x),v0(x))
(9)
的柯西问题.
对每一个固定的ε,假设解(uuε,vε)一致有界:
|uε|≤M, |vε|≤M.
如果方程组(7)有一严格凸熵η(u,v),则有
(10)
或者
(11)
其中c0是一个正的常数.运用证明结论(5)的相同技巧,有

(12)
从而对任意光滑的熵-熵流(η,q),可证明η(uε)t+q(uε)x的H-1紧性.
此处还有些例外.
1.对某些方程组,我们不容易得到一个严格凸熵.
2.对某些方程组,建立的熵-熵流不光滑或者不在C2空间内.
例1研究特殊的二次流方程组
(13)
带有界可测初值
(u(x,0),v(x,0))=(u0(x),v0(x)) (v0(x)≥0)
(14)
的柯西问题广义解的存在性,更多结果见参考文献[3-4].
令映射F:2→2定义为
则
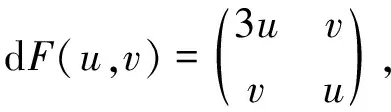
其特征方程为
λ2-4uλ+3u2-v2=0.
于是方程组(13)的两个特征值为
(15)
其相应的右特征向量为
其中s=u2+v2.
方程组(13)的黎曼不变量w(u,v)与z(u,v)为满足
(16)
的函数.方程组(16)的一个解为
经过简单计算,我们有

(17)
因此由式(15)知在(0,0)点λ1=λ2,从而方程组(13)在该点非严格双曲;而且由式(17)知第一、二特征场分别在v=0,u≥0和v=0,u≤0上线性退化.

即
(18)
(19)
由黎曼不变量的定义,容易验证
▽w(u,v)·dF(u,v)=λ2▽w(u,v),▽z(u,v)·dF(u,v)=λ1▽z(u,v).

(20)
(21)
注意到

即得下述形式的熵方程:
(22)
作从(u,v)到(u,s)的变量变换,令
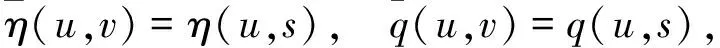
则由链式法则有
于是熵方程(19)变为简单的方程:
ηss=1/4s·ηu u.
(23)
因而相应于熵η的熵流q满足
qu=2uηu+2sηs.
(24)
若函数η=h(s)eku(k∈+)为方程(23)的解,则

(25)
这是经典的Fuchsian方程.
方程(25)具有一个下述级数形式的解:
(26)
其中系数c0为任意正常数,cn满足

于是由二阶线性常微分方程理论知
(27)
为方程(25)的一个与φ1(r)线性无关的解.
若ηk=a(s)φ(r)eku,则由(24)得
从而相应于熵ηk的一个熵流qk为
令η-k=a(s)φ(r)e-ku,则由(24),相应于熵η-k的一个熵流q-k为
关于Fuchsian方程
φ″(r)-(1+c/r2)φ(r)=0 (c∈)
(28)
的两个解φ1(r)和φ2(r)在无穷远处的性态,我们有下述引理:

(29)

(30)
其中c1与c2是适当的正常数.
证明过程见参考文献[2].
(31)
而
(32)
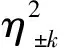
进一步,
(33)
由于
(34)
因此
(35)
(36)
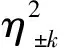
(37)
有
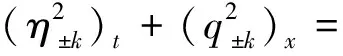
(38)
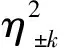

(39)
现在回到式(38),就有
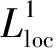
例2欧拉坐标系下的等熵气体动力学方程组
(40)
带有界可测初值
(ρ(x,0),u(x,0))=(ρ0(x),u0(x)),
(41)
的柯西问题.其中,ρ和u分别表示气体的密度和速度,ρ0(x)>0,P=P(ρ)是压强,详见文[5].
对于多方气体,P取特殊形式P(ρ)=cργ,其中γ>1,c是任意正常数,其任意弱熵可以用以下显式公式表示:
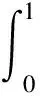
(42)
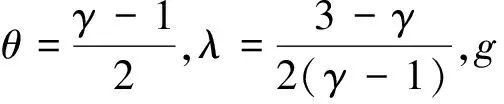
用(η0ρ,q0ρ)乘下面的抛物型方程组
(43)
有
(44)
其中q0是相应于η0的熵流.然后利用严格凸熵
(45)
我们首先得到
(46)



(47)
现在我们研究更一般压强P(ρ)的H-1下的紧性.我们构造一列正则的双曲方程组
(48)
来接近方程组(40),式(48)中的δ>0表示一个正则扰动常数,而扰动压强
(49)
函数P(ρ)∈C2(0,∞)满足
P′(ρ)>0, 2P′(ρ)+ρP″(ρ)>0, ∀ρ>0.
经过简单计算,方程组(48)的两个特征值为
其相应的右特征向量为
方程组(48)的两个黎曼不变量是
其中m=ρu.此外

因此对固定的δ>0,方程组(48)在区域ρ>2δ内严格双曲而在ρ=2δ上非严格双曲;并且两个特征场都在区域ρ≥2δ上真正非线性.
就光滑解而言,方程组(48)等价于如下系统
(50)
特别地,这两个方程组有着相同的熵-熵流.因此方程组(48)的任一熵-熵流(η(ρ,m),q(ρ,m))满足方程组
(51)
从(51)中消去q得
(52)
考虑相关抛物方程组
(53)
带初值
(ρ(x,0),u(x,0))=(ρ0(x)+2δ,u0(x)).
(54)
的柯西问题.
容易验证方程组(40)或(48)有个凸熵
(55)
及相应的熵流
(56)

ε(ρx,mx)·▽2η*(ρ,m)·(ρx,mx)T
(57)

(58)

(59)
设(η(ρ,u),q(ρ,u)),(η(ρ,u),q1(ρ,u,δ))分别为方程组(40),(48)的熵-熵流,这是因为它们和(53)熵相同但是熵流不同.用(ηρ,ηu)乘(59),得
(60)
如果(40)的弱熵有形式η(ρ,u)=ρH(ρ,u),其中H(ρ,u)是任一光滑函数.所以由熵方程(52)得
(61)
其中g(u)是任一光滑函数.上式两端关于ρ积分有
(62)
这是因为η(0,u)=0.所以
(63)
(64)
把等式(63),(64)代入(60)并利用熵方程(52)得
η(ρε,mε)t+q(ρε,mε)x=I1+I2+I3,
(65)
其中
I1=εη(ρε,mε)xx-(q1(ρε,mε,δ)-q(ρε,mε))x,
(66)
(67)
(68)

(69)
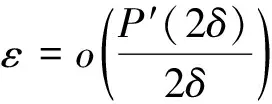

(70)
其中e≥0是常数.利用Vol’pert定理和(70)中给定的极限,有以下估计
(71)
(72)

注1我们只能证明形式为η(ρ,u)=ρH(ρ,u)的弱熵的H-1紧性.对于η(0,u)=0的一般弱熵,H-1紧性仍不明显.
例3研究非线性非严格双曲方程组
(73)
带有界可测初值
(ρ(x,0),u(x,0))=(ρ0(x),u0(x)),ρ0(x)≥0,
(74)

通过简单计算,得到方程组(73)的两个特征值:
λ1=u-θρθ,λ2=u+θρθ
(75)
其相应的右特征量为
r1=(1,-θρθ-1)T,r2=(1,θρθ-1)T;
(76)
其相应的两个黎曼不变量为
z=u-ρθ,w=u+ρθ;
(77)
且
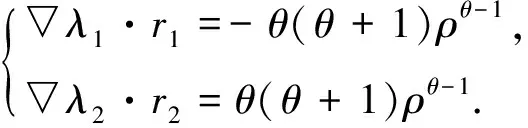
(78)
因此,由式(75)知直线ρ=0上λ1=λ2,从而方程组(73)非严格双曲,由式(78)知γ>3时两个特征场都在ρ=0上线性退化.当1<γ<3时,在ρ=∞上线性退化.
方程组(73)的任一熵-熵流(η(ρ,u),q(ρ,u))满足方程组
(79)
消去q得
ηρρ=θ2ργ-3ηu u.
(80)
现在考虑相关的抛物型方程组
(81)
带初值(74)的柯西问题.
分别用(wρ,wu)和(zρ,zu)乘方程(81),得
(82)
和
(83)
若把(82)和(83)分别视为变量w和z的不等式,则利用极值原理得到估计w(ρε,uε)≤M,z(ρε,uε)≥-M,利用(81)的第一个方程得到ρ≥0.这表明
∑={(ρ,u):w(ρ,u)≤M,z(ρ,u)≥-M,ρ≥0}
是方程组(81)的一个不变域.因此可得到估计0≤ρε≤M1,||uε||≤M1,M1为不依赖于ε的适当常数.
方程组(73)的一类弱熵由
(84)
给出,相应于η0的弱熵流q0则为
(85)
方程组(73)的两类强熵则由如下给出:
(86)
相应于η±的强熵流q±则为
(87)
其中g(ξ)是(-∞,∞)中具有紧支集的光滑函数,且基本解为
(88)
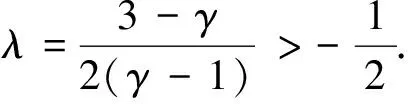
定理2对于柯西问题(81)和(74)的黏性解(ρε(x,t),uε(x,t)),设方程组(73)的熵η(ρ,u)满足
(89)
在0≤ρ≤M1,|u|≤M1上有界,则当ε→0时,
η(ρε(x,t),uε(x,t))t+q(ρε(x,t),uε(x,t))x
(90)

证明利用熵方程(80)可得到方程组(73)的一个凸熵.
(91)

ε(ρx,ux)·▽2η*(ρ,u)·(ρx,ux)T
(92)

(93)

利用熵方程(80)及条件ηρ(0,u)=0,有
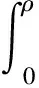
(94)
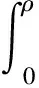
(95)
因此,
(96)
其中M,M2是正常数.
用(η(ρ,u)ρ,η(ρ,u)u)乘(81)得
(97)
利用(96)的第一个估计式和(93)以及ηu的有界性,有

(98)
利用(96)的第二个估计式和(93),并注意到ηu u有界及ηρρ=θ2ργ-3ηu u,有
(99)

定理3对于柯西问题(81)和(74)的黏性解(ρε(x,t),uε(x,t)),当ε→0
ηj(ρε(x,t),uε(x,t))t+qj(ρε(x,t),uε(x,t))x,(j=1,2,3)
(100)

(101)
(102)
η±,η0由(84),(86)给出,qj是相应于ηj的熵流.
证明仅证明(η1,q1)的情况,(ηj,qj),j=2,3的证明过程类似.令τ=ξ-w,则

(103)
因此

(104)
因为-1<2λ<0,所以上式右端第一项当ρ→0时趋于0,在(104)右端的第二项中,令τ=ρθs,则有

(105)
这是由于(ρθ)2λ+1ρ-1=1,所以

(106)
类似地,有

(107)
因此

(108)
所以

(109)
于是把(106)和(109)结合就有η1(ρ,u)ρ|ρ=0=0.显然η1关于变量u光滑,所以利用定理2即得到定理3的证明.
例4带松弛与扩散的一般2×2拟线性守恒律
(110)
带可测初值
(v,u)|t=0=(v0(x),u0(x))
(111)
的柯西问题关于刚性松弛与控制扩散的奇异极限.(110)中的第二个方程包含一个松弛装置,h(v)是u的平衡值,τ是松弛时间;ε是扩散系数.松弛项在一些适当坐标系下的系统中起阻尼作用.
定理4设f,g∈C1(R2),h∈C2(R)且τ=o(ε)(ε→0).如果柯西问题(110)-(111)的解(vε,uε)对任意给定的时间T有先验L∞界:
|(vε,uε)(x,t)|≤M(T), (x,t)∈R×[0,T],
(112)
其中,常数M(T)>0与ε无关,那么存在子列(vεk,uεk),当εk→0.时,强收敛于(v,u).
当使用补偿列紧方法证明定理4时,主要技巧在于证明以下估计.
引理2若柯西问题(110)-(111)的解有先验L∞界(112)且f,g∈C1(R2),h∈C2(R),则
(113)
如果M1τ≤ε对某个大常数M1>0.
证明过程见参考文献[2].
定理4的证明我们把方程组(110)中的第一个方程改写为:
vt+f(v,h(v))x=εvxx+(f(v,h(v))-f(v,u))x.
(114)
设(η(v),q(v))是标量方程
vt+f(v,h(v))x=0
的任一熵-熵流,则用η′(v)乘方程(114),我们有
(115)
其中γi(i=1,2)在u与h(v)之间取值.
由(113)中的估计式,在任意紧集Ω⊂×+上有


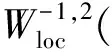
因此由关于标量方程的紧性框架即得{vε}的强收敛性.再由(113)中的第二个估计可得{uε}的强收敛性.这就完成了定理4的证明.
[1]Chen G Q,Lu Y G. The study on the appliaction of the theory of compensated compactness[J].Chinese Science Bulletin,1989(1):641-644.
[2]Lu Y G, Cheng Z X.Hyperbolic conservation laws and compensated compactness method[M].Beijing:Science Press,2011:15-16;42-44;163-164.
[3]Lu Y G. Cauchy problem for a hyperbolic model[J].Nonlinear Anal TMA,1994,23(9):1135-1144.
[4]Lu Y G. Convergence of the viscosity method for a nonstrictly hyperbolic system[J].Acta Math Sci,1992(2):230-239.
[5]Lions P L,Perthame B,Tadmor E.Existence and stablitity of entropy solutions for the hyperbolic systems of istropic gas dynamics in Eulerian and Lagrangian coordinates[J].Comm Pure Appl Math,1996,49(6):599-638.
[6]Lu Y G. The global Hölder-continous solution of isentropic gas dynamic[J].Proc Royal Soc Edinburgh,1993,123(2):231-238.
[7]Chen G Q,Lu Y G.Convergence of the approximation solution solution to isentropic gas dynamics[J].Acta Math Sci,1990(10):39-46.

