拟复射影空间CQn+p中的全实2-调和子流形

马金生,宋卫东

(1.合肥广播电视大学,安徽 合肥 230001; 2.安徽师范大学数学计算机科学学院 安徽 芜湖 241000)

0 引 言

设CQn+p是复n+p维黎曼流形,若其曲率张量取为如下形式:

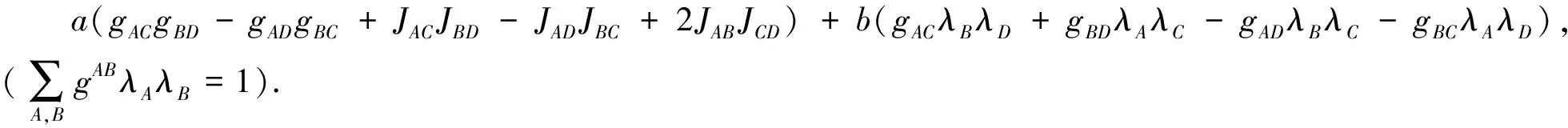
则称CQn+p为拟复射影空间[1].其中a,b是CQn+p上的光滑函数,g为CQn+p上的黎曼度量,J为CQn+p的复结构,λA是CQn+p上的单位向量函数.文献[2-3]讨论了拟常曲率空间中的2-调和子流形,文献[4]讨论了复空间形式中的2-调和子流形,2-调和子流形是极小子流形的推广.本文将外围空间推广到了拟复射影空间,由于拟复射影空间的复杂性给计算及估计带来很多的困难,本文得到如下结果.

定理1设Mn是拟复射影空间CQn+p中n维紧致全实2-调和子流形,则有如下积分不等式:

其中：||B||为Mn的第二基本形式模长;H为Mn的平均曲率.

定理2设Mn是拟复射影空间CQn+p中n维具有平行平均曲率的全实2-调和子流形,||B||2为Mn的第二基本形式模长的平方,则

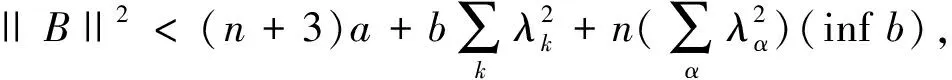
1 预备知识

设Mn是CQn+p中的实n维全实子流形,J为CQn+p的复结构.在CQn+p上选取局部规范正交标架场

e1,…,en,en+1,…,en+p,e1*=Je1,…,en*=Jen,e(n+1)*=Jen+1,…,e(n+p)*=Jen+p.

使得限制于Mn,{e1,…,en}与Mn相切.本文对各类指标取值范围约定如下

A,B,C,…=1,…,n+p,1*,…,(n+p)*;i,j,k,…=1,…,n;

α,β,γ,…=n+1,…,n+p,1*,…,(n+p)*;λ,μ,…=n+1,…,n+p.

令{ωA}是{eA}的对偶标架场,CQn+p的结构方程限制到Mn上有：

(1)

(2)

(3)

(4)

其中B,ξ,Rijkl,Rαβkl分别是Mn的第二基本形式,平均曲率向量场,曲率向量场,曲率张量场,法曲率张量场,是CQn+p的曲率张量场,在标准正交基下gAB=δAB.此时,由于CQn+p是拟复射影空间,那么,

KABCD=a(δACδBD-δADδBC+JACJBD-JADJBC+2JABJCD)+b(δACλBλD+δBDλAλC-δADλBλC-δBCλAλD),

(5)

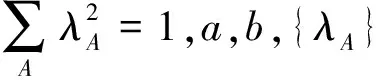
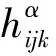
(6)

(7)

以下总假设Mn是拟复射影空间CQn+p中全实2-调和子流形,则

引理1[5]Mn是CQn+p中全实2-调和子流形的条件是

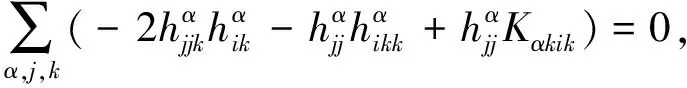
(8)

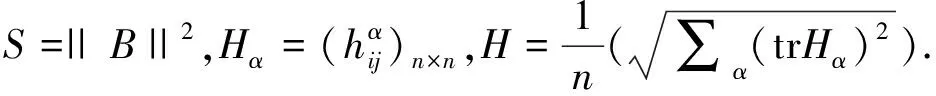
利用式(5)，易得

引理2[6]设Mn是拟复射影空间CQn+p中的任一子流形,则

(9)

2 定理证明

定理1的证明

首先计算Mn的第二基本形式模长平方||B||2的Laplace算子,

由式(6),将式(8)第1式改写为

两端关于指标i求共变导数，并关于i求和,得

调整指标,结合式(8)第2式得,

(10)

由式(5)和式(10)通过计算得

(11)

现在估计式(11)中出现的一些项,首先易见

由于Mn是紧致的,由stokes定理,有

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

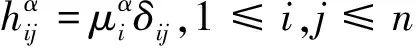
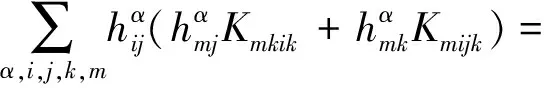
n(a-2|b|)(||B||2-nH2)

(20)

由式(11)～(20)及引理2,以及Mn的紧致性,经整理即可完成定理1的证明.

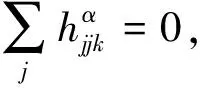
(21)

由Cauchy不等式,得

(22)

由式(5),得

(23)

(1)当infb≥0时,由式(33)得

(24)

若处处有

(25)

则唯一的可能是n2H2=0,即Mn是CQn+p中的极小子流形.

(26)

于是由式(23)得

(27)

(28)

则唯一的可能是n2H2=0,即Mn是CQn+p中的极小子流形.

即完成定理2的证明.

参考文献:

[1]宋卫东,朱岩.拟复射影空间中的2-全实伪脐子流形[J].吉林大学学报：理学版，2012,50(4):673-676.

[2]宋卫东.关于拟常曲率空间中的2-调和子流形[J].数学物理学报：A辑，2006,26A(3):426-430.

[3]邓义华.拟常曲率空间中的2-调和子流形为极小子流形的条件[J].数学的实践与认识,2009,39(8):234-237.

[4]Zhu Yecheng, Song Weidong. 2-Harmonic Submanifolds in a Complex Space Form[J]. Journal of Mathematical Research & Exposition,2008,28(3):727-732.

[5]姜国英.2-调和映照及其第一、第二变分公式[J].数学年刊,1986,7A:389-402.

[6]Chen Bangyen, Ogiue K. On Totally Real Submanifolds[J]. Trans AMS，1974,193:257-266．

[7]孙宏安,钟定兴.复射影空间的全实2-调和超曲面[J].数学研究与评论,1999,19(2):431-436.

[8]宣满友,刘继志.拟常曲率黎曼流形中具有平行平均曲率向量的子流形[J].数学研究,2001,34(4):379-385.