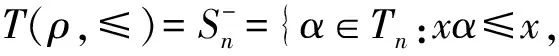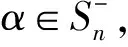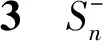T(ρ,≤)的Green关系和正则元

王珍珍, 杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

1 引言和准备知识

设Xn={1,2,…,n},Tn表示Xn上的全变换半群,设ρ是Xn上的一个等价关系,≤是Xn/ρ上的一个全序,在文献[1]中研究出全变换半群Tn的所有极大半传递子幺半群,其中首次引入了Tn的子半群

T(ρ,≤)={α∈Tn:(xα)ρ≤xρ,∀x∈Xn},

称其为划分递减变换幺半群.

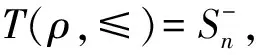
并在文[3]中又刻划出T(ρ,≤)的自同构群.在此我们进一步研究T(ρ,≤)的Green关系和正则元.

2 Green关系

在文[4]中给出了Green关系的定义.在本节中给出T(ρ,≤)上的Green关系如下.

定理1令α,β∈T(ρ,≤),那么

2) (α,β)∈当且仅当imα=imβ且对任意的s∈imα,y,z∈Xn有min{yρ:y∈sα-1}=min{zρ:z∈sβ-1};

xα=yα⟹xαγ=yαγ⟹xβ=yβ;xα=yα⟸xβδ=yβδ⟸xβ=yβ.

于是kerα=kerβ.又有

(xα)ρ=(xβδ)ρ≤(xβ)ρ; (xβ)ρ=(xαγ)ρ≤(xα)ρ.

及≤是Xn/ρ上的一个全序可知(xα)ρ=(xβ)ρ.

充分性 由kerα=kerβ可设

其中α,β∈T(ρ,≤).则aiρ≤xρ,biρ≤xρ(x∈Ai,i=1,2,…,k).又由对任意的x∈Xn有(xα)ρ=(xβ)ρ知aiρ=biρ(i=1,2,…,k).于是可以定义δ,γ如下形式:

(2)充分性 由imα=imβ且对任意的s∈imα,y,z∈Xn有min{yρ|y∈sα-1}=min{zρ|z∈sβ-1}.可设μsρ=min{yρ|y∈sα-1}=min{zρ|z∈sβ-1}=νsρ,其中μs∈sα-1,νs∈sβ-1(μs与νs可以相同,μs,νs∈Xn).于是定义δ,γ如下形式:

yδ=νs(y∈sα-1,s∈imα);zγ=μs(z∈sβ-1,s∈imβ).

故δ,γ∈T(ρ,≤)且α=δβ,β=γα.因此(α,β)∈.

必要性 若(α,β)∈,那么(α,β)∈(Tn),于是imα=imβ.也知道存在δ,γ∈T(ρ,≤)使得α=δβ,β=γα.设对任意的s∈imα=imβ,t∈Xn,tρ=min{yρ|y∈sα-1}且t∈sα-1,则

tδβ=tα=s.

从而

tδ∈sβ-1.

因此

tρ≥(tδ)ρ≥min{zρ|z∈sβ-1}.

也就是

min{yρ|y∈sα-1}≥min{zρ|z∈sβ-1}.

类似证明min{zρ|z∈sβ-1}≥min{yρ|y∈sα-1}.故min{yρ|y∈sα-1}=min{zρ|z∈sβ-1}.

(3)由(1)和(2)知(3)显然成立.

φ:imα→imβ

使得任意的z∈imα,x,y∈Xn有

(z,zφ)∈ρ,min{xρ|x∈zα-1}=min{yρ|y∈(zφ)β-1}.

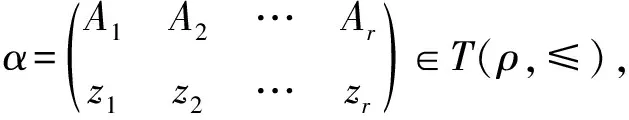
则由已知可令

那么对任意的x,y∈Xn,zi∈imα(i=1,…,r)有

(zi,ziφ)∈ρ,min{xρ|x∈Ai}=min{yρ|y∈Bi}(i=1,…,r).

又由β∈T(ρ,≤)知(ziφ)ρ≤min{yρ|y∈Bi}(i=1,…,r).从而ziρ≤min{yρ|y∈Bi}(i=1,…,r).于是可作γ如下:

所以imα=imγ且对任意的zi∈imα(i=1,…,r),x,y∈Xn有

min{xρ|x∈ziα-1}=min{xρ|x∈Ai}=min{yρ|y∈Bi}=min{yρ|y∈ziγ-1}.

知(α,γ)∈.也有kerγ=kerβ且对任意的z∈Xn有

(zγ)ρ=ziρ=(ziφ)ρ=(zβ)ρ(i=1,…,r)

也存在γ∈T(ρ,≤)使得αγβ,那么imα=imγ且对任意的zi∈imα(i=1,…,r),x,y∈Xn有

min{xρ|x∈ziα-1}=min{yρ|y∈ziγ-1}, kerγ=kerβ

且对任意的z∈Xn有

(zγ)ρ=(zβ)ρ.

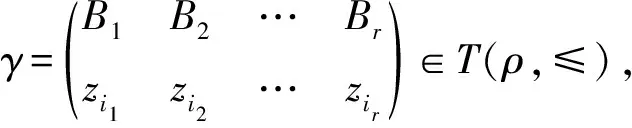
其中zi1,…,zir是z1,…,zr的一个排列且设zi=zij(i=1,…,r,ij=i1,…,ir).那么由任意的z∈Xn有(zγ)ρ=(zβ)ρ知

zijρ=ljρ(j=1,…,r).

由任意的zi∈imα(i=1,…,r),x,y∈Xn有min{xρ|x∈ziα-1}=min{yρ|y∈ziγ-1}知

min{xρ|x∈Ai}=min{xρ|x∈ziα-1}=min{yρ|y∈zijγ-1}=min{yρ|y∈Bj}=min{yρ|y∈ljβ-1}.

因此可设φ是从imα到imβ的一个双射且ziφ=lj(i,j=1,…,r).于是对任意的zi∈imα(i=1,…,r),x,y∈Xn有(ziφ)ρ=ljρ=zijρ=ziρ且

min{xρ|x∈ziα-1}=min{xρ|x∈Ai}=min{yρ|y∈ljβ-1}=min{yρ|y∈(ziφ)β-1}.

3 正则元

如果一个半群S的元a满足a=aba(b∈S),那么称a为正则元.如果S的所有元都是正则元,那么称S为正则半群.在本节中将给出T(ρ,≤)的正则元.

其中a1ρ≤x1ρ(x1∈A1),a2ρ≤x2ρ(x2∈A2),…,arρ≤xrρ(xr∈Ar).那么α为正则元当且仅当aiρ∩Ai≠∅(i=1,2,…,r).

证明必要性 由α为正则元知存在β∈T(ρ,≤)使得αβα=α.那么可令

aiβ=bi(i=1,2,…,r).

于是bi∈Ai且biρ≤aiρ(i=1,2,…,r).又由定义知aiρ≤biρ(i=1,2,…,r).所以

aiρ=biρ(i=1,2,…,r),

从而

bi∈(aiρ)∩Ai(i=1,2,…,r).

故aiρ∩Ai≠∅(i=1,2,…,r).

充分性 若aiρ∩Ai≠∅(i=1,2,…,r),不妨设bi∈(aiρ)∩Ai(i=1,2,…,r),则biρ=aiρ(i=1,2,…,r).可作β如下:

bi=aiβ(i=1,2,…,r);y=yβ(y≠ai).

于是β∈T(ρ,≤)且对任意的x∈Xn有

xαβα=aiβα=biα=ai=xα(i=1,2,…,r),

则αβα=α.故α是正则元.

定理3T(ρ,≤)是正则半群当且仅当ρ=Xn×Xn或Xn/ρ={{1},Xn-{1}}({1}

证明充分性 如果ρ=Xn×Xn,那么T(ρ,≤)=Tn;如果Xn/ρ={{1},Xn-{1}}且{1}

必要性 假设ρ≠Xn×Xn且Xn/ρ≠{{1},Xn-{1}}({1}

1)若|Z1|=1,则Z1={1}且t>2.那么可设Z2={2,…,r}(2≤r≤n-1),…,Zt={k,…,n}(r

可知α∈T(ρ,≤),但由引理1知α不是正则元与已知矛盾,假设不成立.

2)若|Z1|≥2,则t≥2.不妨设Z1={1,2,…,r}(1

可知α∈T(ρ,≤),但由引理1知α不是正则元与已知矛盾,假设不成立.

由定理3立刻有

推论1若T(ρ,≤)是正则半群,则|T(ρ,≤)|=nn或|T(ρ,≤)|=(n-1)n.

由引理1立刻有

进而由定理3立刻有

[1]Yang Xiuliang, Yang Haobo. Maximal half-transitive submonoids of full transformation semigroups[J]. Adv Math,2011,40(5):580-586.

[2]Umar A. On the semigroups of order-decreasing finite full transformations[J]. Proceedings of the Royal Society of Edinburgh,1992,120A:129-142.

[3]Yang Haobo, Yang Xiuliang. Automorphisms of partition order-decreasing transformation monoids[J]. Semigroup Form,2012,85:513-524.

[4]Howie J M. Fundamentals of semigroups theory[M]. Oxford: Oxford University Press,1995.