流水工序调度与生产效率的关系模型分析

季香君，马立红，刘紫玉

(河北科技大学经济管理学院，河北石家庄 050018)

流水工序调度与生产效率的关系模型分析

季香君，马立红，刘紫玉

(河北科技大学经济管理学院，河北石家庄 050018)

提出一种基于粒子群算法的流水工序调度任务优化模型。利用流水工序调度任务的特点得到流水工序时间约束条件，利用粒子群算法的原理建立流水工序调度任务优化模型，利用粒子群算法对模型进行求解。仿真实验表明，利用该算法能够得到流水工序调度问题的最优解，提高生产效率。

流水工序；调度；混合粒子群算法；生产效率

随着工业化水平的不断提高和科学技术的不断发展，制造业之间的竞争越来越激烈[1-2]。流水工序合理的生产调度因其能够帮助企业提高生产效率[3]、增强企业竞争力，因此越来越受到人们的重视。流水工序的调度问题属于强NP完全问题，优化调度的实质就是多项工序共享一定的资源时，这些资源不能让所有工序都以最佳状态独享资源的处理要求，因此需要对流水工序进行合理安排，以确保在对资源共享的同时保证生产效率[4-5]。流水工序具有动态性、无序性、多目标性、多约束性等特点[6]，使得流水工序的调度问题成为难解的NP完全问题。流水工序调度问题已经成为当前工业生产领域研究的热门问题[7-10]。

传统的流水工序调度优化算法是基于启发式搜寻算法的流水工序调度优化算法、基于神经网络算法的流水工序调度优化算法和基于遗传算法的流水工序调度优化算法，其中应用最广泛的是基于遗传算法的流水工序调度优化算法。这些调度优化算法存在一个共同缺陷，就是只能适用于规模较小的流水工序调度问题，一旦流水工序规模增大，将会出现计算量呈指数级增大的缺陷，导致调度任务效率降低，生产效率下降。

为了避免上述弊端，本文分析了一种基于粒子群算法的流水工序调度优化算法。根据流水工序的调度任务特点建立流水工序调度任务模型，利用粒子群算法对调度任务寻求最优解。仿真实验表明，利用粒子群算法能够提高流水工序调度任务的效率，提高了生产效率，效果令人满意。

1 传统遗传算法的流水工序调度优化原理

遗传算法是根据自然界中优胜劣汰的基本法则演化而来的一种解决非线性复杂问题的基本方法。其基本原理是利用遗传算法，按照一定的规则，从父系群体中选取适合要求的个体进行选择、交叉、变异等基本遗传操作，产生带有父系基因的后代，反复进行遗传操作后就能够得到最优解。遗传算法相对于普通的搜寻方法具有良好的鲁棒性。

1.1遗传算法在流水工序调度问题的实现过程

1.1.1 选择合适的染色体编码方式

流水工序具有动态性、多目标性等特点，利用传统的二进制编码方式无法满足生产要求。因此遗传算法应用到流水工序方面一般选用加工顺序的直接编码方案。设长度是L的染色体，将其分为n段长度分别为l1,l2,…，ln的子染色体，依次对应流水工序的各个加工序列，染色体上的基因gab表示加工工序，1≤a≤n,1≤b≤La。图1表示流水工序染色体的编码方案。

图1 流水工序染色体编码方案Fig.1 Water process chromosome coding scheme

1.1.2 对流水工序的种群初始化操作

为了能够得到流水工序的最优调度方案，必须生成由不同调度方法构成的调度群体，进行初始化操作，并以此为起点进行下一步遗传操作。在流水工序调度中，设在t时刻各道工序的前列工序均可利用的工序集合为可利用集，记为U(t)，流水工序的可利用集合的子集是可利用集合与流水工序序列的交集。

初始化操作的过程如下：在初始时刻，可利用集合U(0)={(1,1),(2,1),…,(n,1)}，表示n个作业的第1道工序构成集合。当一个工序进行作业时，将离开可利用集；当一个工序结束后，若此工序之后还有未完工序，则将未完的工序加入到可利用集合中，利用可利用集合能够生成可行调度方法的集合。

1.1.3 建立流水工序调度个体适应度函数

遗传算法在进行最优调度方案求解的过程是封闭的，只能根据个体适应度函数对最优解的优劣进行判断，适应度越高的个体生存机会就越高。利用目标函数能够转化得到适应度函数。在流水工序调度最优方案的问题中，适应度函数只能是正数，式(1)能够表示流水工序调度问题的个体适应度函数：

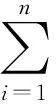
(1)

式中：wij表示流水工序个体i在工序j中的权重；T用于描述流水工序调度过程中某个体的调度时间。

1.1.4 设计合适的选择遗传算子

利用选择遗传算子能够根据适应度函数的值选择合适的流水工序调度方案个体进行遗传操作。设选择某个流水工序调度方案个体的概率是Y，则利用式(2)能够表示选择遗传算子的函数：

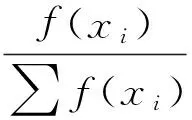
(2)

式中：xi表示调度方案集合中第i个调度方案；f(xi)表示第i个调度方案的适应度；∑f(xi)表示所有调度方案个体适应度之和。

1.1.5 确定交叉算子

由于流水工序调度问题的编码方案与一般的编码方案不同，因此，其交叉算子也与一般的交叉算子不同。在2个调度方案个体进行交叉时，必须在对应的子染色体上交叉，而不能跨段交叉，如图2所示。

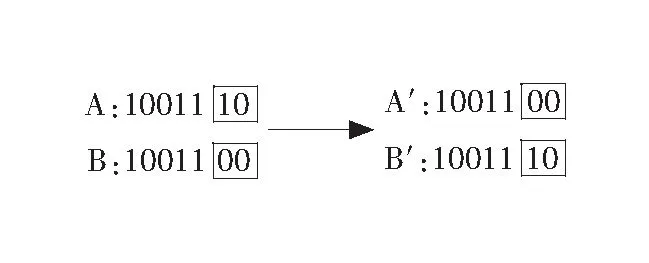
图2 子染色体对应交叉示意图Fig.2 Schematic diagram of chromosome corresponding cross

1.1.6 确定修正算子

利用遗传算法求解流水工序中最优调度方案的问题中，会出现不符合现实工艺流程的染色体，导致算法得不到最优解。利用修正算子能够避免此种情况的发生。对于不正确的调度方案，对染色体(调度方案)上的基因(工序)进行判断，看是否符合工艺流程标准。如果不符合，则重新对工序进行排序，直至达到工艺流程要求为止。

1.2遗传算法的缺陷

在流水工序调度最优解的实际应用中，由于工序规模难以确定，所以一旦工序规模增加，算法的计算量将呈指数级增加，不容易得到局部最优调度方案的解，且收敛速度变慢，导致调度任务效率降低，生产效率降低，无法满足工业生产的要求。为了避免传统遗传算法的弊端，本文提出一种基于粒子群算法的流水工序调度方案优化方法。

2 基于粒子群算法的流水工序调度任务优化模型

2.1流水工序调度问题的约束条件

在生产过程中，调度的任务是针对某项具体的生产加工任务，通过安排合理的加工工序和设备，达到提高生产效率的目的。流水工序的调度问题需要满足以下约束条件：1)每个工件需要若干道加工工序；2)每个工件的加工工序不能改变；3)每台设备只能进行一个工序，本道工序结束后工件才能进行下一个工序；4)在同一时刻，同一工件不能同时被2台及以上的机器加工；6)每一道工序的加工时间都要在要求范围之内。

根据以上阐述，流水工序的调度任务就是通过合理安排加工工序和设备，缩短每一道工序的加工时间，提高生产效率。利用式(3)能够描述流水工序调度任务，即各个工序的最小化完工时间：

(3)

式中：ck表示第k台机器结束工序的时间。

2.2基于粒子群算法的流水工序调度任务优化模型

粒子群算法源于人们对鸟群捕食的研究，是一种群智能的优化算法。该算法最大的特点是以独立的粒子为个体，并赋予每个粒子简单的行为规则，使粒子群具有全局寻优的智能化特性。利用粒子群算法解决复杂问题具有计算量小、收敛速度快、鲁棒性强的特点。

2.2.1 基于粒子群算法的流水工序调度优化算法实现步骤

1)对粒子种群(流水工序调度的集合)进行初始化，设粒子种群中有n个粒子(流水工序调度方案)，随机产生n个解。

2)根据目标函数，计算每个粒子的适应度值。

3)将各个粒子的适应度值与之前经历的调度方案的适应度值进行对比，如果这个值比之前的好，则保留当前的调度方案。

4)将各个粒子的适应度值与全局经历的调度方案的适应度值进行对比，如果这个值比之前全局经历的好，则保留当前的调度方案。

5)利用式(4)迭代方程对流程工序的组合进行更新：

vi(t+1)=ωvi(t)+c1r1(pi(t)-xi(t))+

c2r2(pg(t)-xi(t))xi(t+1)=

xi(t)+vi(t+1)。

(4)

式中：vi表示第i个调度方案的完工时间；ω是惯性系数，表示上一次迭代速度对本次迭代速度的影响；c1和c2表示学习因子，正常情况下，c1=c2；r1,r2表示互相独立的2个函数；xi表示第i套调度方案在所有解的位置；pi表示单个调度方案从初始时刻到当前时刻搜寻到的最优解；pg表示全局从初始时刻到当前时刻搜寻到的最优解。

6)设置一个合适的适应度值作为终止迭代的调度，得到最优调度方案后终止粒子种群的迭代。

2.2.2 相关参数设置

流水工序的调度问题具有动态性、无序性、多目标性、多约束性等特点，在进行编码时，一个粒子代表一种调度方案，所有同一工件的序号作为工序编号，根据工序编号在染色体出现的顺序决定工件的工序。

迭代次数：设置粒子种群迭代次数为40次。

惯性系数：惯性系数的值越大越有利于搜寻全局最优解，其值越小越有利于算法的收敛性。因此，利用自适应函数能够根据需要调节惯性系数值的大小。利用式(5)能够描述自适应度与惯性系数的关系：

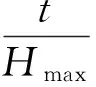
(5)

式中：Hmax表示最大迭代次数。利用自适应度与惯性系数的函数关系能够减少0.4～0.9的线性。

学习因子：一般由经验值决定，在流水工序调度问题中设为3。

2.2.3 流水工序调度任务模型的建立

流水工序调度要解决的核心问题就是降低各个工序完成的时间，提高生产效率。因此，目标函数就是最大完成时间的最小值。根据上述要求建立的流水工序调度任务的目标函数模型如式(6)所示：

min(T(jm))=
min(max[T(1),T(2),…,T(i),…,T(m)]。

(6)

式中：T(i)表示第i道工序的完成时间；T(jm)表示整个加工任务结束时使用的时间。

利用式(7)能够对粒子的适应度进行评估：

f=100×Zbest/T(jm)。

(7)

式中：Zbest表示根据生产运营需要设定的生产流程结束时最优完成时间。利用粒子算法进行具体的流水工序调度最优解的具体过程如图 3所示。

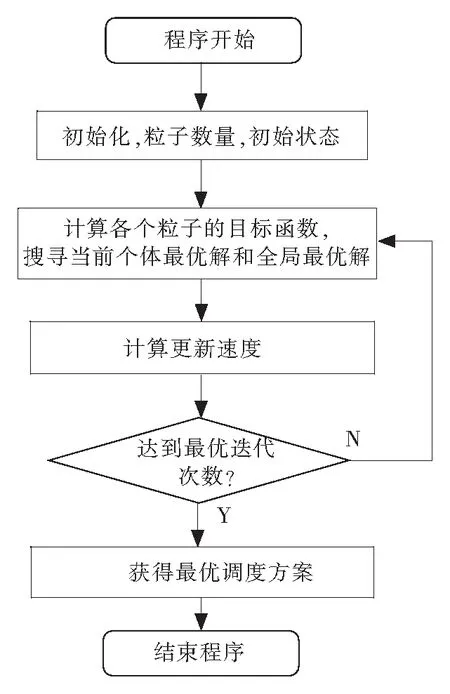
图3 利用粒子群算法搜寻过程Fig.3 Searching process by using particle swarm optimization algorithm

2.2.4 利用粒子群算法对模型求解

利用上述建立的流水工序调度任务模型，对生产过程中的工件、机器和加工工序进行调度安排，工件加工过程符合本文流水工序优化模型中的约束条件。在加工过程中的每道工序的加工时间各不相同。设在某一流水工序中需要对6个工件和6台机器进行调度安排，每个工件分别在一台机器上加工一次。每个工件的加工工序与每道工序需要的时间如表1所示。

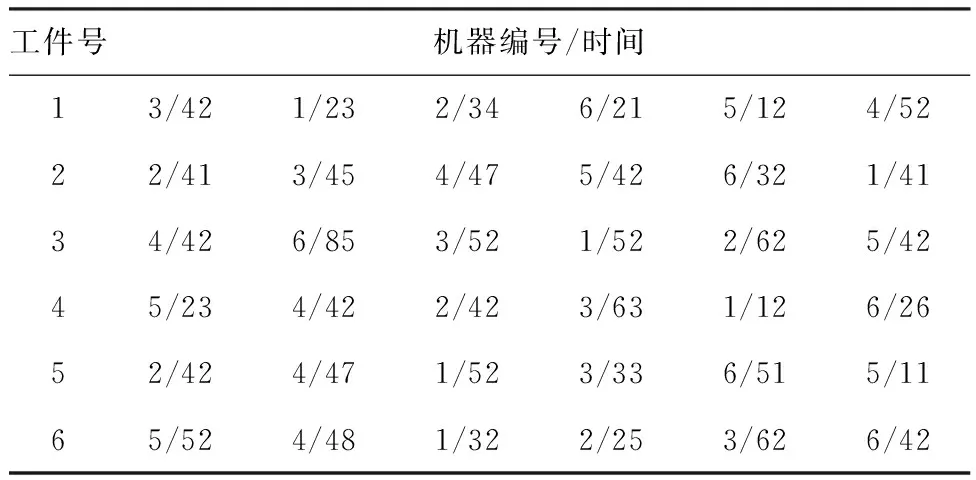
表1 加工工序对应时间表

注：时间单位为min。

利用粒子算法对流水工序调度安排的结果如图4所示。

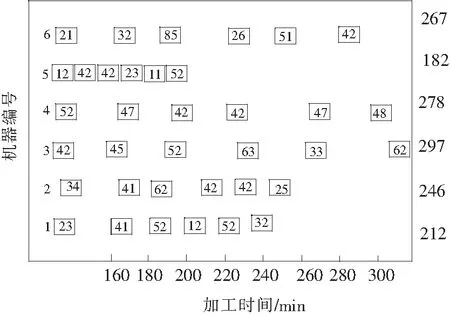
图4 粒子算法搜寻结果Fig.4 Particle algorithm search result

从图4可知，利用粒子算法对流水工序调度方案搜寻的最小任务完工时间为182 min，充分体现出本文算法的有效性。

3 仿真实验结果及分析

为了验证本文算法的有效性和优越性，需要进行一次仿真实验。实验对象为某水产品加工企业生产车间，加工某批次水产品的流水加工工序，设一次流水工序中有10个工件和10台机器，设置迭代次数为100次，实验重复进行100次。实验结果如图5所示。

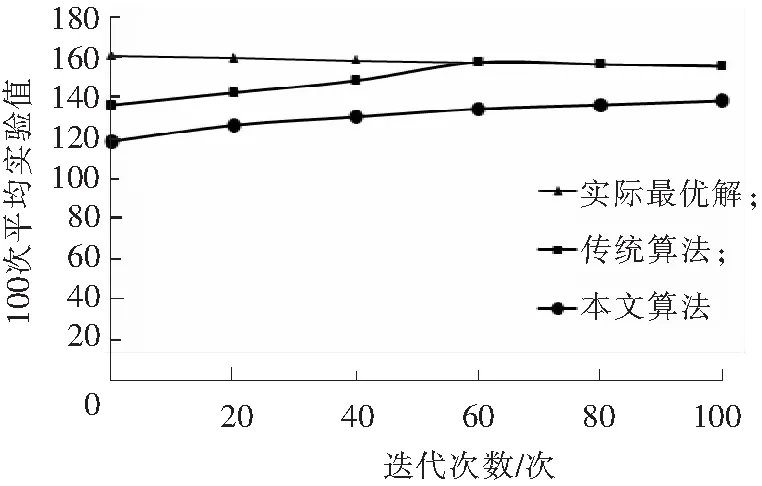
图5 实验结果Fig.5 Experimental results

根据实验结果可知，在流水工序规模较大时，利用本文算法能够在迭代次数较少的情况下得到最优解。传统遗传算法由于计算量过大导致收敛速度降低，容易得到局部最优解，难以得到全局最优解。

实验中不同算法的机器平均利用率对比结果如图6所示。

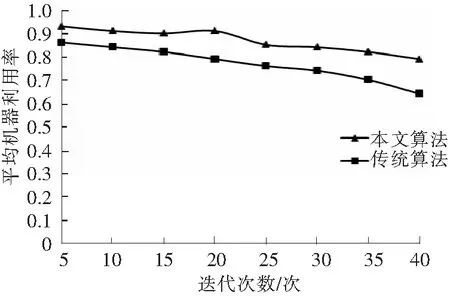
图6 不同算法的机器平均利用率Fig.6 Average utilization rates of machine under different algorithms

从实验结果可知，利用本文算法能够有效提高实验水产品企业生产车间机器的平均利用率，提高了该水产品企业的生产效率，相对传统的遗传算法具有很大的优越性。

4 结 语

流水工序的调度问题具有很强的动态性、有序性、多目标性、多约束性等特点，利用传统的遗传算法会因收敛速度慢导致生产效率降低，不能满足生产过程的需要。本文提出一种基于粒子群算法的流水工序的调度优化算法。仿真实验表明，本算法能够提高机器的利用率，缩短生产加工工序的完成时间，提高生产效率，体现出本算法的有效性和优越性。

/

[1] IBARRA O,KIM C.Heuristic algorithms for scheduling independent tasks on non-identical processors[J].Journal of the ACM,1977,77(2):280-289.

[2] 李艳玲，潘杰义，陈玥希.基于DEA的企业技术创新效率评价研究[J].河北工业科技，2005，22(2)：74-76. LI Yanling,PAN Jieyi,CHEN Yuexi.Research on evaluating the efficiency of enterprise technology innovation based on DEA method[J].Hebei Journal of Industrial Science and Technology,2005,22(2):74-76.

[3] SHEN Hua, WEI Feifei. Grid resources pricing model[J]. Journal of Hubei University of Technology, 2006,21(4): 45-50.

[4] ZOU L D.Single machine group scheduling problem based on improved genetic algorithm[J].Computer Simulation, 2011,27(4):308-313.

[5] FOSTER I,KESSELMAN C,TUECKE S.The anatomy of the grid:Enabling scalable virtual organization[J].High-Performance Computing Applications,2001,15(3):200-222.

[6] GE Xiang,ZHANG Li. A new quantum genetic algorithm and its application[J].Journal of Electronics, 2004,32(3):17-30.

[7] ARMSTRONG R,HENSGEN D,KIDD T.The relative performance of various mapping algorithm is independent of sizable variance in run-time predictions[A].7th IEEE Heterogeneous Computing Workshop(HCW’98)[C].[S.l.]:[s.n.]，1998.79-87.

[8] LIAN Zhigang，GU Xingsheng，JIAO Bin．A similar particle swarm optimization algorithm for permutation flowshop scheduling to minimize makespan[J]．Applied Mathematics and Computation，2006，175(1)：773-785．

[9] PAN Q K， WANG L．Nidle permutation flow shop scheduling based on a hybrid discrete particle swarm optimization algorithm[J]．International Journal of Advanced Manufacturing Technology，2007(7):1252-1256.

[10] YANG Qingyun，SUN Jigui，ZHANG Juyang,et al．A hybrid discrete particle swarm algorithm for open-shop problems[A]．Proceedings of the 6th International Conference on Simulated Evolution and Learning[C]．Hefei:[s.n.]，2006.158-165．

Relational model analysis of assembly line scheduling and efficiency

JI Xiangjun， MA Lihong， LIU Ziyu

(School of Economics and Management, Hebei University of Science and Technology, Shijiazhuang Hebei 050018, China)

Based on particle swarm algorithm, a kind of flow process scheduling optimization algorithm is presented in this paper. Time constraint condition is obtained according to the characteristics of assembly line scheduling, and assembly line scheduling optimization model is established by using particle swarm algorithm principle, then the particle swarm algorithm is used for the solution of the model. Simulation results show that the algorithm can get the optimal solution of assembly line scheduling problem, so as to improve the production efficiency.

assembly line; scheduling; hybrid particle swarm optimization algorithm; production efficiency

1008-1534(2014)04-0291-05

2014-01-16;

2014-04-04;责任编辑：张士莹

河北省自然科学基金(F2012208018)；河北省高等学校科学技术项目(ZD2014027)

季香君(1971-)，女，河北唐山人，副教授，硕士，主要从事管理科学与工程、企业管理方面的研究。

E-mail：jxjrsc@126.com

TP391

A

10.7535/hbgykj.2014yx04005

季香君，马立红，刘紫玉.流水工序调度与生产效率的关系模型分析[J].河北工业科技,2014,31(4):291-295. JI Xiangjun，MA Lihong，LIU Ziyu.Relational model analysis of assembly line scheduling and efficiency[J].Hebei Journal of Industrial Science and Technology,2014,31(4):291-295.