基于极点配置算法的列车横向半主动悬挂自适应PID控制系统设计

金光大， 金炜东， 李 明

(西南交通大学电气工程学院，四川成都 610031)

基于极点配置算法的列车横向半主动悬挂自适应PID控制系统设计

金光大， 金炜东， 李 明

(西南交通大学电气工程学院，四川成都 610031)

为了使PID控制器具备自适应能力，以适应列车受到外部环境扰动时产生的结构参数变化，使用了增量式数字PID控制器，将PID控制器与极点配置控制算法结合，利用极点配置算法在线实时优化kP，kI，kD参数，设计了自适应极点配置PID控制器，实现了kP，kI，kD参数的自动校正。最后给出基于极点配置自适应PID的高速列车半主动悬挂控制系统的设计方案，利用MATLAB-Simulink搭建仿真平台并进行仿真。仿真结果表明：基于极点配置算法的列车半主动悬挂自适应PID控制系统能够有效降低列车横向振动。

自适应；PID；悬挂系统；控制

列车在国内外均是人员出行和货物运输的非常重要且不可或缺的交通工具，由于列车的广泛应用性，对列车运行的稳定性和舒适性提出了较高的要求，而横向振动正是这一问题的关键所在[1-2]。在列车的运行中横向振动幅值的大小与轨道不平顺，牵引力和制动力都有着直接和间接的关系，克服和减小列车的多自由度随机振动一直以来是一个备受关注的问题[3-4]。随着中国铁路运输的发展，列车逐步提高运行速度，这个问题变得更加重要，悬挂系统正是解决该问题的设备与装置。悬挂系统是一系列装置的组合体，包括轮对与构架，构架与车体之间多个弹性元件和阻尼元件，起到减小振动的作用[5-6]。

1 列车半主动悬挂系统的提出

列车的悬挂系统分为被动悬挂，半主动悬挂和全主动悬挂，其中被动悬挂系统通过弹性元件和阻尼元件储存和耗散振动能量，不需要外界提供能源，其参数和性能是不可调节的。同样不需要外界提供能源，但是将被动悬挂中不可调的阻尼原件替换为阻尼值可调节的可变阻尼器，根据不同的路况和外界条件能够实时改变阻尼值，这种悬挂系统称为半主动悬挂[7-10]。将被动悬挂系统中的不可变的弹性原件和阻尼原件替换为可主动产生阻尼力的作动器，这种作动器需要额外提供能源才能工作，根据不同的路况提供给列车不同的阻尼力，已达到最优的减振效果，这种悬挂系统称为全主动悬挂[11]。被动悬挂、半主动悬挂和全主动悬挂系统的示意图如图1所示。

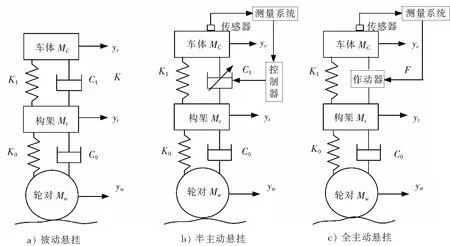
图1 列车悬挂系统示意图Fig.1 Train suspension system diagram

由上述3种悬挂系统的工作原理可知，全主动悬挂由于能够主动提供可控的阻尼力，可达到最优的减振效果，但是全主动悬挂系统需要耗费额外的大量能源，使用价格昂贵的作动器，结构较为复杂，一旦发生故障，则会严重影响列车的运行。半主动悬挂的减振效果不如全主动悬挂，但是优于被动悬挂，可以说半主动悬挂的目的就是能够通过调节阻尼器的阻尼值来尽量模拟全主动悬挂的控制效果，而且不需要额外提供能源，不需要作动器，造价较低，当系统发生故障时可方便地转变为被动悬挂，能够保证列车的安全运行，所以尽管半主动悬挂系统的减振效果不如全主动悬挂系统，但是仍然获得了较为广泛的认可和关注[12-14]。

2 列车自适应半主动悬挂控制系统设计

2.1极点配置自适应PID控制结构

极点配置自适应PID控制系统是一种应用广泛的自适应控制方法，这种方法与系统辨识是密不可分的[15]。极点配置自适应PID的控制思想是通过系统辨识在线的估计和拟合未知被控对象的模型，根据在线辨识的结果优化自校正控制器的参数，使系统达到预先设想的目标。该系统一般是双控制环结构，外环是常规的反馈控制环，内环有2个作用：系统辨识和控制器参数的校正与优化。图2即为极点配置自适应PID控制系统的基本原理图。由图2中可以看出，本文采用17自由度列车横向半主动悬挂模型作为被控对象，17自由度分别为车体和2台转向架的横移，侧滚和摇头以及4个轮对的横移和摇头，通过在线辨识得到被控对象的输入输出模型，针对该模型进行极点配置，使配置后的极点在期望的位置上，进而改善系统的动态和静态性能。PID控制器有较强的鲁棒性和广泛的应用性，如果能够根据一定的策略自动校正PID控制器的参数，不失为一种好的控制方法，列车的运行线路很长，常常会遇到不同的扰动和路况，单一不变的PID参数不能使列车在任何路况下都运行在最优状态下，所以需要根据不同的扰动和路况对PID参数进行实时调节，才能取得较好的控制效果。

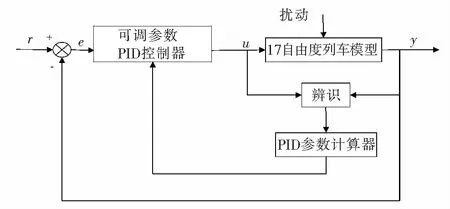
图2 极点配置自适应PID控制结构图Fig.2 Pole placement adaptive PID control structure diagram

2.2极点配置的实现

使用在自适应控制中应用较为广泛的CARMA(controller auto-regressive integrated moving average)模型：

A(q-1)y(k)=q-dB(q-1)u(k)+C(q-1)v(k),

(1)

其中

q-1为延迟算子，先使用增广递推最小二乘法对CARMA模型中的未知参数进行辨识，再将系统的反馈控制律设计为

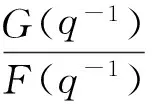
(2)

式中：

F(q-1)=1+f1q-1+…+fnfq-nf，

(3)

G(q-1)=g0+g1q-1+…+gngq-ng。

(4)

将式(2)代入式(1)，整理得

[A(q-1)F(q-1)+q-dB(q-1)G(q-1)]y(k)=

C(q-1)F(q-1)v(k),

(5)

可见，通过在线辨识得到的系统输入输出模型的特征多项式为

A0=A(q-1)F(q-1)+q-dB(q-1)G(q-1)。

(6)

设系统期望的特征多项式为

Am=C(q-1)T(q-1)，

(7)

其中

(8)

式(8)中，1/ti为相应的稳定极点，本文中考虑到最佳二阶工程参数，将期望的闭环系统设计为自然振荡频率ω=10 rad/s和阻尼系数ξ=0.7的二阶系统，超调量σ约为4.3%，调整时间ts约为0.42 s(Δ=5%)，其闭环特征多项式为

T(s)=s2+2ξωs+ω2=s2+14s+100。

(9)

对式(9)使用反向差分进行离散化，这里的延迟算子q-1和离散时间系统常用的z-1是具有同样意义的，根据拉氏变换和Z变换的关系有：q-1=e-Ts，T为采样周期，再将e-Ts展开为无穷级数得：

q-1=e-Ts=1-Ts+…。

(10)

对式(10)取一阶近似得

q-1=1-Ts，

则有

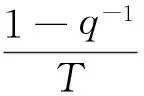
(11)

将式(11)代入式(9)，并取T=0.1得式(9)的离散化为

T(q-1)=1-q-1+0.292 9q-2。

(12)

由式(12)可知期望的闭环极点为

p1=0.5+j0.207 1，p2=0.5-j0.207 1。

为了实现极点配置，就要使系统的特征多项式与期望的特征多项式相等，综合式(6)、式(7)和式(12)得到

A(q-1)F(q-1)+q-dB(q-1)G(q-1)=

C(q-1)T(q-1)。

(13)

式(13)的解法与丢番图方程的解法是类似的，通过令等号两边q-1同次幂的项系数相等即可确定F(q-1)和G(q-1)中的未知系数，为了保证式(13)有解，需要使A(q-1)F(q-1)与q-dB(q-1)G(q-1)阶次相等，C(q-1)T(q-1)的阶次小于或等于A(q-1)F(q-1)和q-dB(q-1)G(q-1)的阶次，即

(14)

把式(13)代入式(5)整理简化，即可得到系统经过极点配置后的闭环方程：

(15)

由式(15)可见，系统的特征多项式为期望的特征多项式T(q-1)。

2.3PID参数的优化

首先介绍一下本文所使用的增量式PID控制器，增量式PID算法如式(16)所示：

Δu(k)=kP[e(k)-e(k-1)]+kIe(k)+

kD{[e(k)-e(k-1)]-[e(k-1)-

e(k-2)]}。

(16)

其中kP，kI和kD分别为比例，积分和微分参数，并且

(17)

对式(16)进行化简整理，式(16)可以表示为

Δu(k)=g0e(k)+g1e(k-1)+g2e(k-2),

(18)

其中

(19)

用q-1作为单位延迟算子，则对式(18)进行进一步整理，可得

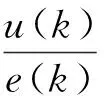
(20)

式(20)可表示为

F(q-1)u(k)=G(q-1)e(k)=

G(q-1)[r(k)-y(k)],

(21)

其中

(22)

考虑到在列车横向半主动悬挂控制系统中，参考输入r(k)总是0，则式(21)可写为

F(q-1)u(k)=-G(q-1)y(k)。

(23)

将式(23)代入式(1)中，整理得

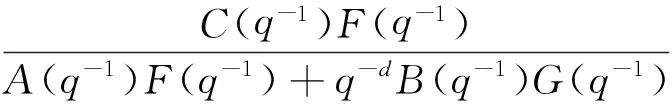
(24)

由式(24)可见系统的特征多项式为

A0=A(q-1)F(q-1)+q-dB(q-1)G(q-1)。

(25)

比较式(25)与式(6)可知，使用增量式PID控制器与使用自适应极点配置控制器的特征多项式恰好是相同的，因此可以同样使用极点配置的方法使得PID控制器中的kP，kI和kD参数实现在线自我校正，自动寻优，仍然使用式(7)，式(12)和式(13)来实现自适应PID控制器的极点配置，由式(7)，式(12)和式(13)确定了G(q-1)中的未知参数g0，g1和g2后，为了获得在线优化后的PID参数，需要解式(19)这个线性方程组，由式(19)本身可知，解该线性方程组显然是非常简单的，完全不会影响控制系统的实时性，最后把解得的kP，kI和kD参数赋给参数可变的PID控制器，即实现了自校正PID控制。

3 基于Simulink的列车半主动悬挂自适应PID控制系统仿真

采用Simulink对车辆半主动悬挂系统进行数字仿真，如图3所示。

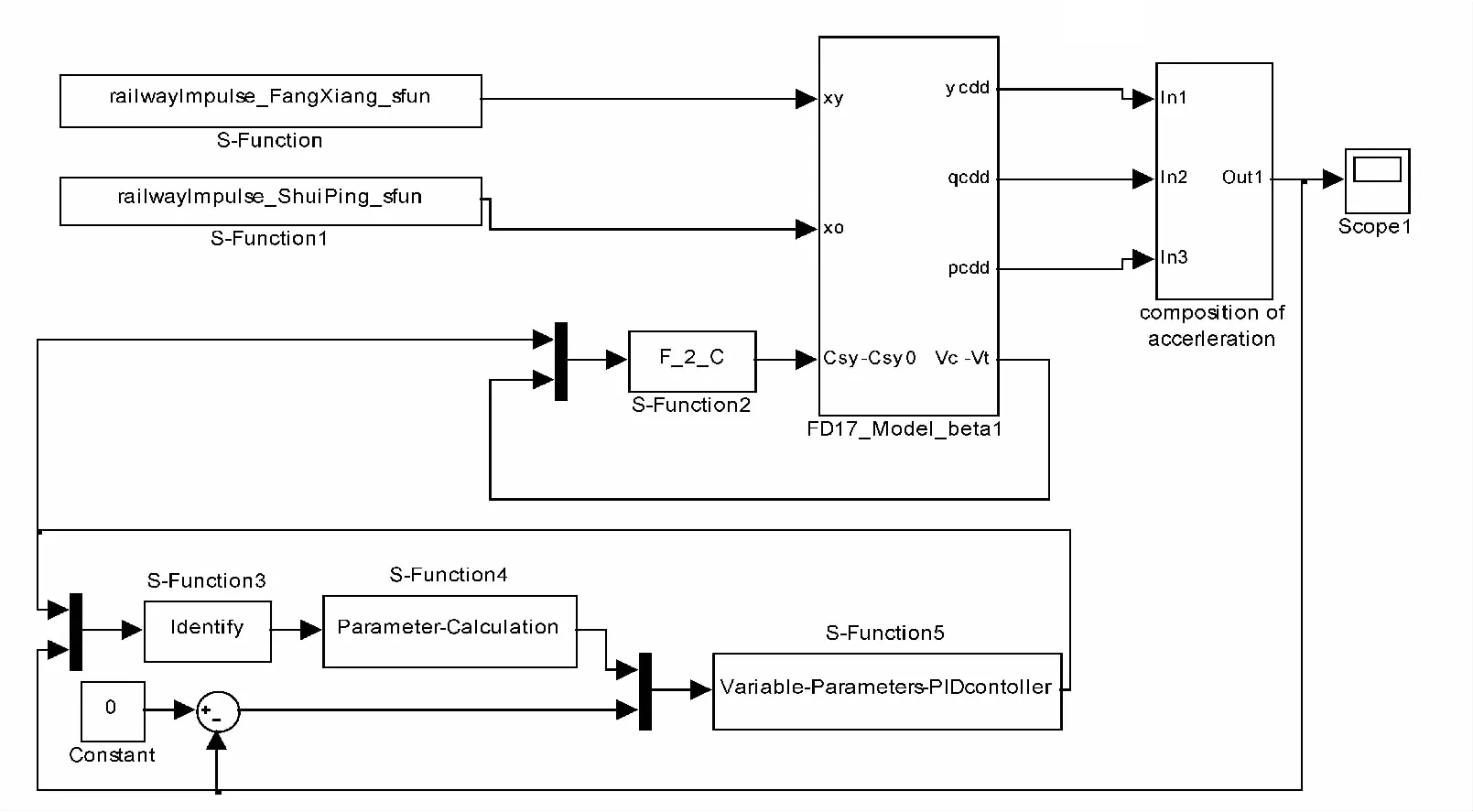
图3 车辆半主动悬挂系统Simulink仿真结构图Fig.3 Simulink simulation diagram of vehicle semi-active suspension system

车体的横向振动情况可由振动加速度时域图比较直观的反映出来，如图4所示。图4中把半主动悬挂与被动悬挂的车体横向振动加速度进行了对比，通过该时域图可以对某一时刻车体在被动和半主动悬挂2种不同悬挂方式下的横向振动幅值进行观察，可以看出相对于被动悬挂，自适应控制取得了一定的控制效果，与被动悬挂相比较车体横向加速度的时域幅值有所下降。

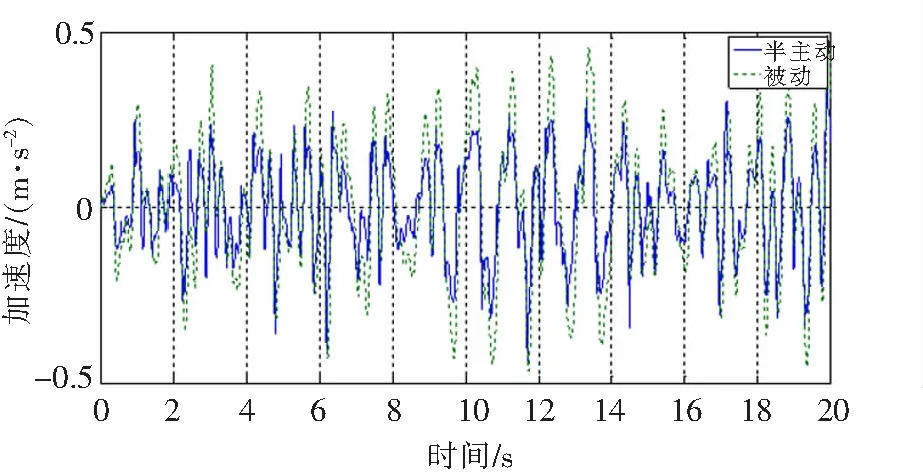
图4 车体横向振动加速度时域图Fig.4 Train lateral vibration acceleration time domain diagram

图5为功率谱图，从功率谱图中可以看出相对于被动悬挂，半主动悬挂自适应控制的车体横向振动加速度在频率低于10 Hz的低频带得到了一定程度的控制，尤其在人体能明显感知振动的频带0.7～3.5 Hz改善效果较为明显。

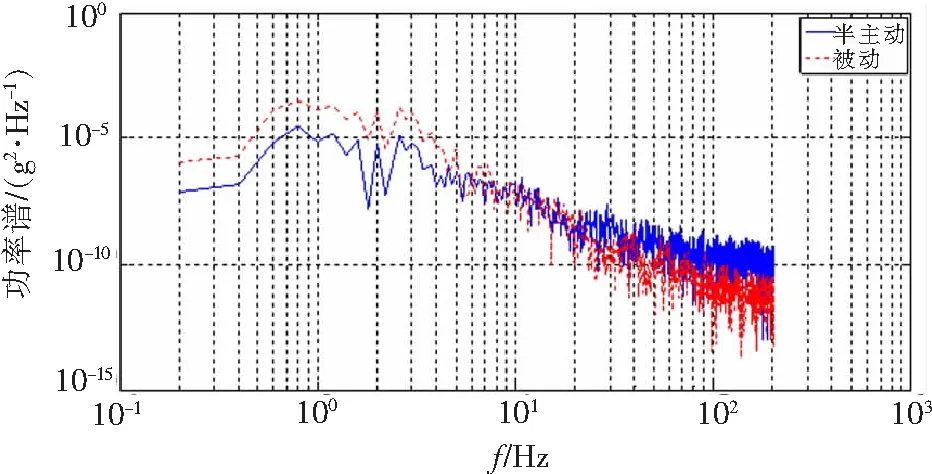
图5 车体横向振动加速度功率谱图Fig.5 Train lateral vibration acceleration power spectrum diagram

图6为频域图，通过频域分析可以看出列车车体的横向振动加速度主要集中在低频段0.5～10 Hz，相对于被动悬挂，半主动悬挂自适应控制的车体横向加速度的频域幅值均有所下降。

图6 车体横向振动加速度频谱图Fig.6 Train lateral vibration acceleration frequency spectrum diagram

相比于被动悬挂系统，基于极点配置自适应PID的半主动悬挂控制系统的车体横向加速度有较大减小，其最大值由0.487 6 m/s2降低到0.312 4 m/s2，改善35.9%，其均方根由0.376 4 m/s2下降到0.278 1 m/s2,改善26.13%。

4 结 语

通过仿真分析可知，将自适应控制理论与方法应用于列车的半主动悬挂控制是可行的，自适应控制方法取得了较好的控制效果，基于极点配置的自适应PID控制器与传统的PID控制器较为相似，但是其与传统的PID控制器相比可以自动校正比例、积分和微分3种参数，适应性更强，并且继承了传统PID控制器的鲁棒性，具有较强的可应用性。

/

[1] 岳三玲，卜继玲，傅茂海．基于Simulink的车辆动力学仿真模型研究[J]．机械制造与自动化，2010, 39(1)：127-130． YUE Sanling, BU Jiling, FU Maohai.Research on dynamic simulation models of vehicle system based on Simulink[J].Machine Building & Automation, 2010,39(1):127-130.

[2] 郁家杰．基于DMC的车辆横向半主动悬挂控制[D]．成都：西南交通大学，2010. YU Jiajie.Vehicle Lateral Semi-Active Suspension Control Based on DMC [D].Chengdu:Southwest Jiaotong University,2010.

[3] 郝莉红，王志腾，陈 洪．基于MatlabSimulink对半主动悬架的Fuzzy-PID控制仿真研究[J]．河北工业科技，2013,30(1)：42-46． HAO Lihong,WANG Zhiteng,CHEN Hong.Simulation of Fuzzy-PID control of semi-active suspension based on MatlabSimulink[J].Hebei Journal of Industrial Science and Technology,2013,30(1):42-46.

[4] SARMA G N,KOZIN F.An active suspension system design for the lateral dynamic of a high-speed wheel-rail system[J].Journal of Dynamic Systems Measurement and Control,1971,86(4):233-241.

[5] SINHA P K, WORMLEY D N, HEDRICK J K.Rail passenger vehicle lateral dynamic preformance improvement through active control[J].Transaction of ASME,1978,100(4):270-283.

[6] GOODALL R M, KORTUEM W.Active controls in ground transportation:A review of the state-of-the-art and future potential[J].Vehicle System Dynamic,1983,12(4/5):225-257.

[7] MORTLAND K,HEDRICK J K.Dynamic performance improvement through active control[J].Transaction of ASME,2011,126(2):109-111.

[8] CELNIKER G W, HEDRICK J K.Rail vehicle activesuspensions for lateral ride and stability improvement[J].Transaction of the ASME,1981,104(7):100-106.

[9] GOODALL E M.Active railway suspension:Implementation status and technological trends[J].Vehicle System Dynamics,1998(12):87-117.

[10] THOMPSON G A.An active suspension with optimal linear state feedback[J].Vehicle System Dynamics,2009(5):187-203.

[11] HEDRICK J K.Railway vehicle active suspension[J].Vehicle System Dynamics,1993(11):267-283.

[12] KWOK K E,SHAH S L,CLANACHAN A S,et al.Evaluation of a long-range adaptive predictive controller for computerized drug delivery systems[J].IEEE Transactions on Bio-medical Engineering,2005,42(1):79-86.

[13] HIRATA T.Control of railway vehicle active suspension[J].Automatica,1995,31(1):13-20.

[14] KARNOPP D.Design principles for vibration control systems using semi-active dampers[J].Journal of Dynamites Systems Measurement and Control,1990,112(3):448-455.

[15] 单 鑫，魏 兵，张会玲．基于自适应模糊PID控制的中央空调冷冻水系统仿真研究[J]．河北工业科技，2013,30(6)：479-483． SHAN Xin,WEI Bing,ZHANG Huiling.Simulation study of the central air conditioning chilled water system based on adaptive fuzzy PID control[J].Hebei Journal of Industrial Science and Technology,2013,30(6):479-483.

Design of adaptive PID control system of vehicle lateral semi-active suspension based on pole placement algorithm

JIN Guangda, JIN Weidong, LI Ming

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China)

In order to let the PID controller to have adaptive ability, suiting to the changing structural parameters when the train is interfered by the external environment, incremental digital PID controller is used. The adaptive pole placement PID controller is designed by combining PID controller and the pole placement algorithm to optimize thekP,kIandkDparameters online and correct themselves automatically. Then, based on the pole placement algorithm adaptive PID controller, the semi-active suspension control system of the high-speed trains is presented. The simulation results by using MATLAB-Simulink show that lateral vibration of the train is effectively reduced by the semi-active suspension adaptive PID control system.

adaptive; PID; suspension system; control

1008-1534(2014)04-0271-05

2014-03-11;

2014-04-06;责任编辑：陈书欣

国家自然科学基金(61134002)

金光大(1986-)，男，辽宁新民人，硕士研究生，主要从事电气系统控制及信息技术方面的研究。

金炜东教授，博士生导师。E-mail: wdjin@home.swjtu.edu.cn

TP29

A

10.7535/hbgykj.2014yx04001

金光大， 金炜东， 李 明.基于极点配置算法的列车横向半主动悬挂自适应PID控制系统设计[J].河北工业科技,2014,31(4):271-275. JIN Guangda ,JIN Weidong, LI Ming.Design of adaptive PID control system of vehicle lateral semi-active suspension based on pole placement algorithm[J].Hebei Journal of Industrial Science and Technology,2014,31(4):271-275.