基于双非线性反馈控制的五维超混沌系统的分析与电路实现

，，，，

(浙江工业大学 技术与教育发展研究中心，浙江 杭州 310023)

自上世纪60年代，Lorenz发现了第一个混沌系统以来，混沌问题的研究越来越受到关注[1]，尤其是实际应用方面更受学术界的青睐，以至于较快地促进了混沌技术的应用和推广.我们知道同步控制技术是制约混沌技术应用的关键问题，如1999年Chen等利用反控制方法实现了对偶的混沌系统同步控制[2-3]，该系统很快在不同领域的研究和具体技术实践中得以广泛应用，随后的Lorenz系统[4-6]和Chen系统[7-9]之间的转换系统Lü系统[8，10]也在同步技术的支撑下发挥了很重大的作用.当然，随着人们对混沌系统的认识不断深化，新的混沌系统不断被发现和提出，如多涡卷混沌系统[11-12]，多翼混沌系统[13-14]，分数阶混沌系统[15-16]等，这些新颖混沌系统的硬件电路较易实现和有效的同步控制，在混沌保密通讯、图像加密和信息工程中破解了诸多难题.

在混沌技术识别和实现方面，线性控制法、非线性控制法、正弦激励法和反馈控制等是比较常用技术和方法，基于双非线性反馈控制技术，在混沌系统构造方面，通过低维的系统来构造高维的混沌系统，如基于三维混沌系统可以实现四维混沌、五维混沌和超维混沌的构造，并通过仿真论证和电路实现，形成了比较理想的研究成果.笔者在研究过程基于三阶Lü混沌系统，利用两个非线性控制器，构造出一个全新的五阶混沌系统，同时在两个参数k1，k2动态配合下，分析新系统所呈现的周期、混沌和超混沌现象，并探究在一定的范围内的复杂的混沌特性[17]，这些指标通过动力学算法进行论证并经过图表进行呈现，如平衡点、相图、Poincare截面图、Lyapunov指数谱、分岔图[17-18]等.当然，在分析的同时，借助Multisim电路模拟软件设计出相应的电路，并通过数字示波器观察生成的图像并与Matlab的仿真图像进行对比，来进一步验证了五维混沌系统的动力学行为.笔者详细给出了五阶超混沌系统的相关特性、电路原理和实现方法，这样对研究同类的混沌系统和实现同步控制具有借鉴和指导作用.

1 五维混沌系统的模型

Lü系统是一个经典的三维混沌系统，其表示为

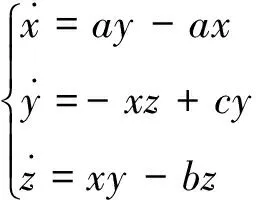
(1)

在上述模型的基础上，增加两个非线性状态反馈控制器u和v，得到一个五维受控混沌系统.系统的描述为

(2)

其中：x,y,z分别为系统的变量；u和v为反馈控制器的状态变量；a，b，c分别为常数；k1,k2分别为控制增益.当选择合适的a，b，c，k1，k2时，系统就可产生各种复杂现象.

2 五维受控混沌系统的特性分析及Matlab仿真

2.1 耗散性和证明吸引子的存在性

常数a=36，b=3，c=20，暂取控制参数k1=-1，k2=-2进行特性分析.

对于式(2)有

(3)

式(2)的相空间内的相体积逐渐缩小到零，其为耗散系统，而在所有轨道上运动的点集都被吸引到一个相体积为零的一点上，这一组点集就是混沌吸引子.式(2)以幂指数的形式可表示为

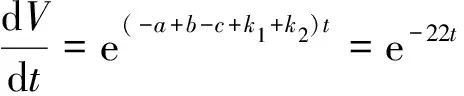
2.2 平衡点及不稳定性

当式(2)取2.1中参数时，令方程右边等于零，即

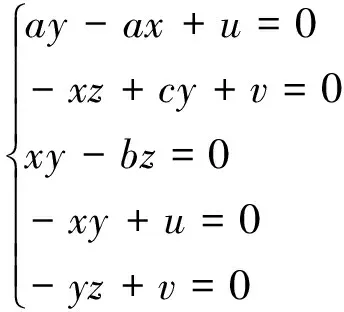
(4)

可得到式(2)的三个平衡点S0(0，0，0，0，0)，S1(6.119，7．372，15．037，-45．112，-55．429)，S2(-6．492，-5．500，11．902，-35．707，32.732).

在S0(0，0，0，0，0)平衡点处对式(2)进行线性化得到其Jacobian矩阵[20]，即

(5)

令det(J-λI)=0，得到平衡点S0(0，0，0，0，0)相应的5个特征根分别为λ1=-36.000，λ2=-3.000，λ3=-2.000，λ4=-1.000，λ5=20.000.其中λ5为正实根，而λ1，λ2，λ3，λ4为负实根，因此，平衡点S0为不稳定鞍点.

在平衡点S1采用相同的方法得到其相应特征根为λ1=-25.758，λ2=-3.171，λ3=-0.959，λ4=3.944+9.949i，λ5=3.944-9.949i.其中λ1，λ2，λ3为负实根，λ4，λ5为一具有正实部的共轭复根，因此，平衡点S1是不稳焦结点.

在平衡点S2也采用相同的方法得到其相应特征根为λ1=-28.762，λ2=-2.883，λ3=-1.045，λ4=5.345-8.302i，λ5=5.345-8.302i.其中λ1，λ2，λ3为负实根，λ4，λ5为一具有正实部的共轭复根，因此，平衡点S1也是不稳焦结点.

由上述分析可知：式(2)的3个平衡点都是不稳定的，其中S0为不稳鞍点；而另外2个平衡点S1和S2都是不稳焦结点.

2.3 仿真混沌吸引子

仍取上述参数，利用Matlab仿真软件，采用五阶龙格-库塔算法，得到该五维受控混沌系统在x-y，x-z，x-u，x-v及u-v的瞬态相轨迹图，如图1所示.

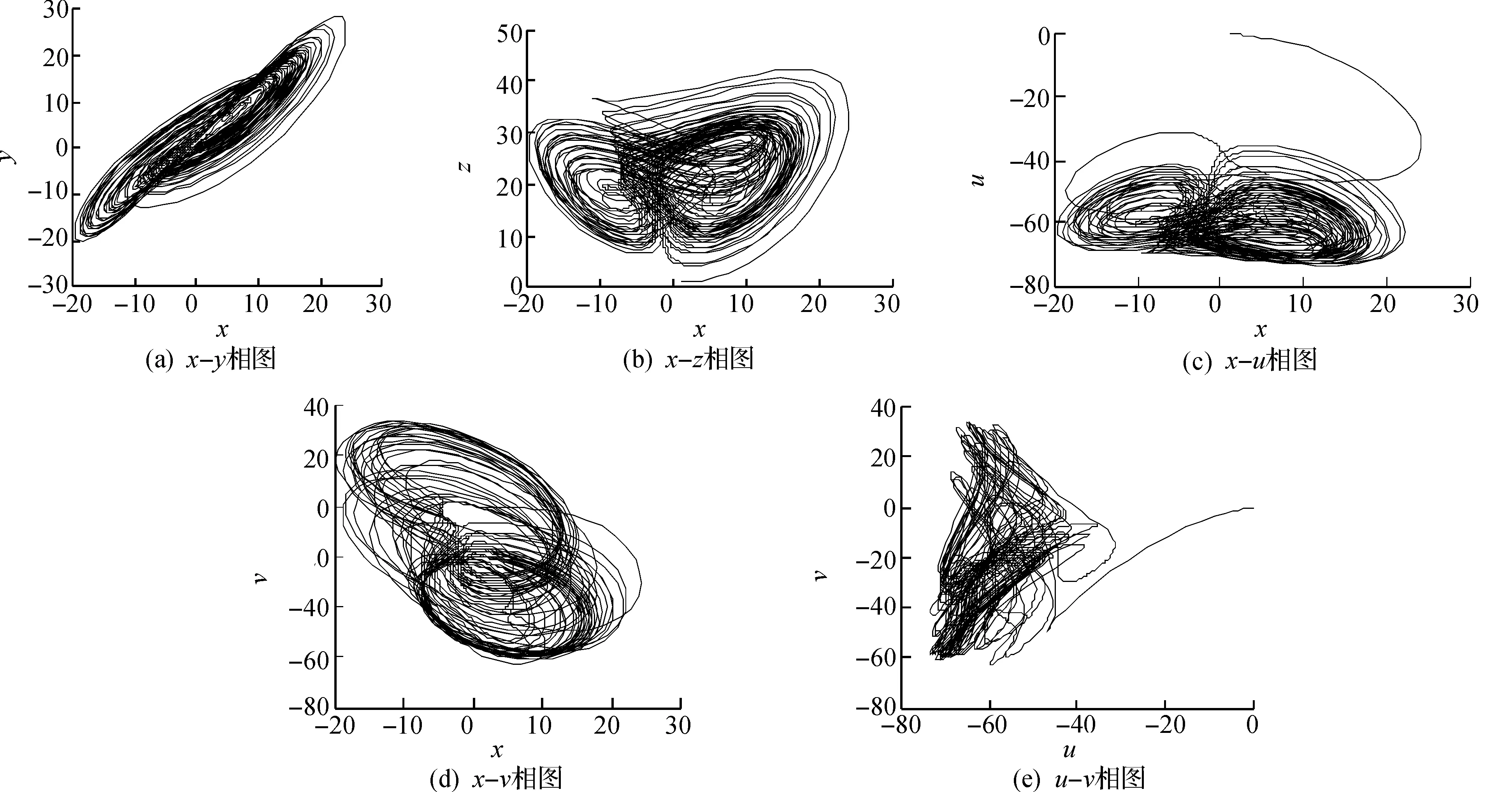
图1 式(2)的混沌吸引子相图

从仿真结果可见，该系统是一个混沌系统，相轨在各个方向都有分离，且运动具有各态历经性，即任一条运动轨迹都几乎通过吸引子上所有点.

2.4 不同参数下的Lyapunov指数

为了更好地认识这个五维受控混沌系统的动力学特性与控制参数k1，k2的关系，我们进一步从Lyapunov指数着手，研究在不同参数条件下的轨迹运动形式.在此之前有必要先陈述一下各运动形式与Lyapunov指数的关系.

定义1对于一个5维超混沌的系统，该系统具有5个Lyapunov指数.当最大的Lyapunov指数等于零，其他4个Lyapunov指数都小于零时，系统做周期运动；当最大的Lyapunov指数大于零，有1个Lyapunov指数等于零，其他3个Lyapunov指数都小于零时，系统做混沌运动；当最大的2个Lyapunov指数都等于零，其他3个Lyapunov指数都小于零时，系统做拟周期运动；当最大的2个Lyapunov指数都大于零，有一个Lyapunov指数等于零，其他2个Lyapunov指数小于零时，系统做超混沌运动.

根据定义1，我们通过调节其中一个控制参数，取几个特定的值，用Matlab计算Lyapunov指数来判断式(2)的运动形式，如表1所示.

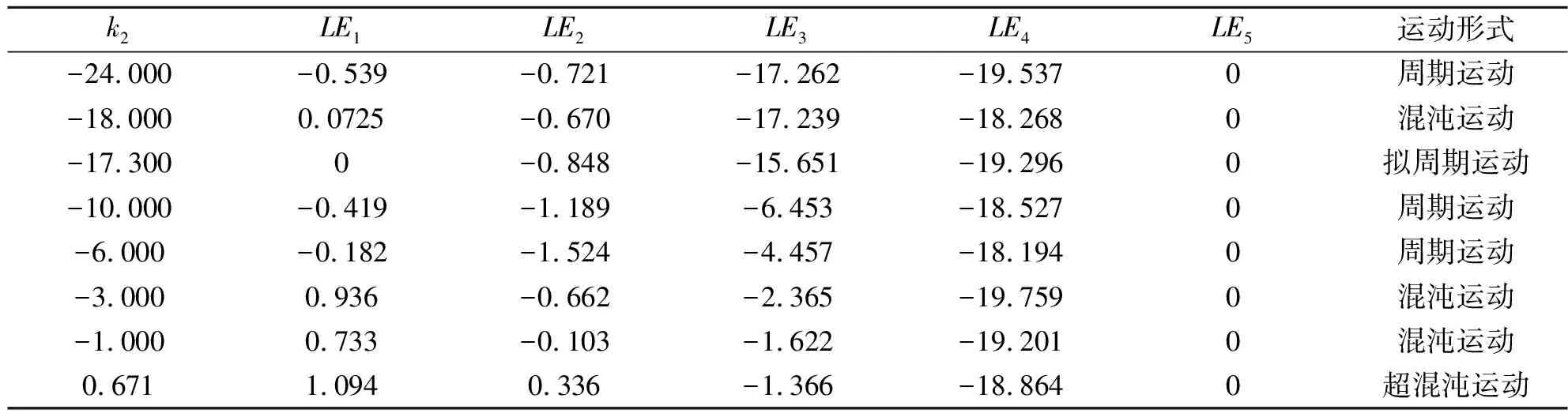
表1 不同参数k2对应的Lyapunov指数和运动形式

2.5 不同控制参数下的Lyapunov指数谱、分岔图和poincare截面图

从2．4的内容可知：Lyapunov指数能根据其正负数值判定系统轨迹线之间彼此吸引和排斥，从而较好地反应系统的运动形式.另外，Lyapunov指数谱能更直观地观察出不同参数范围内的系统状态.下面给出在2个控制参数k1，k2的Lyapunov指数谱(LE谱)，如图2所示.需要说明的是在控制参数k1变化时，式(2)的第4个Lyapunov指数是一个比较小的负数，所以在图2(a)中没有列出.

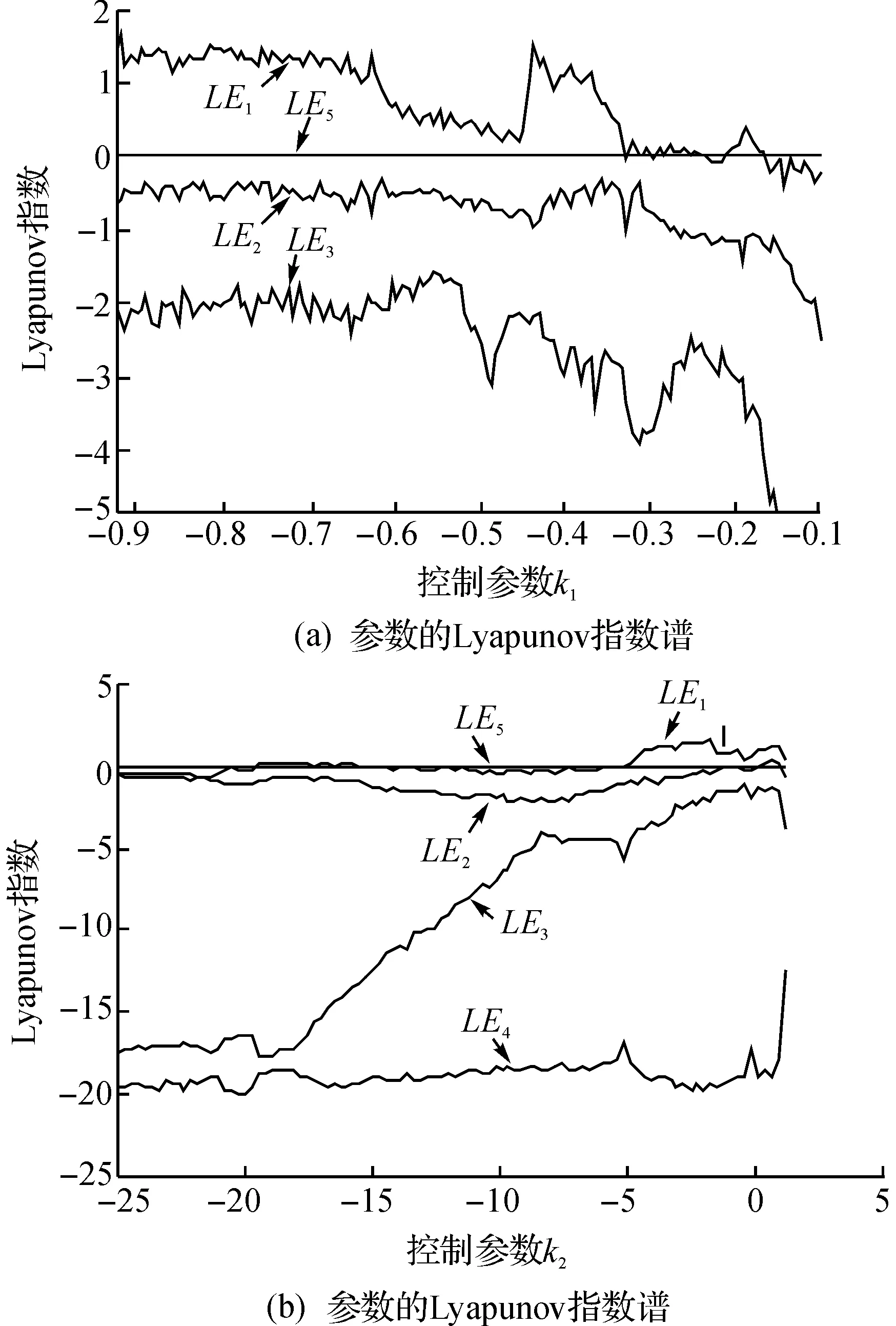
图2 式(2)的Lyapunov指数谱

图2(a)是关于k1的Lyapunov指数谱.固定参数a=36，b=20，c=3，k2=-2，改变参数k1.

1) 当参数k1∈{[-0．333，-0．325]，[-0.302，-0．290]，[-0．235，-0．210]}时，式(2)的Lyapunov指数满足LE1，LE2，LE3，LE4<0，LE5=0，系统是周期的.

2) 当参数k1∈{[-0．922，-0．333]，[-0．325，-0．314]，[-0．290，-0．253]，[-0．210，-0．167]}时，式(2)的Lyapunov指数满足LE1>0，LE2，LE3，LE4<0，LE5=0，系统是混沌的.

3) 当参数k1∈{[-0．314，-0．302]，[-0．253，-0．235]}时，式(2)的Lyapunov指数满足LE1=0，LE2，LE3，LE4<0，LE5=0，系统是拟周期的.

4) 当参数k1∈{-1．505，[-1．318，-1．258]}时，式(2)的Lyapunov指数满足LE1，LE2>0，LE3，LE4<0，LE5=0，系统是超混沌的.

图2(b)是关于，k2的最大Lyapunov指数谱.固定参数a=36，b=20，c=3，k1=-1，改变参数k2.

1) 当参数k2∈{[-25．000，-19．441]，[-15．472，-5．152]}时，式(2)的Lyapunov指数满足LE1，LE2，LE3，LE4<0，LE5=0，系统是周期的.

2) 当参数k2∈{[-19．441，-17．598]，[-17．065，-16．533]，[-16．276，-15．472]，[-5．152，0．141]}时，式(2)的Lyapunov指数满足LE1>0，LE2，LE3，LE4<0，LE5=0，系统是混沌的.

3) 当参数k2∈{[-17．598，-17．065]，[-16．533，-16．276]}时，式(2)的Lyapunov指数满足LE1=0，LE2，LE3，LE4<0，LE5=0，系统是拟周期的.

4) 当参数k2∈[0．141，1．032]时，式(2)的Lyapunov指数满足LE1，LE2>0，LE3，LE4<0，LE5=0，系统是超混沌的.

从上述分析看出：该系统在参数变化过程中运动方式相互转变，历经了拟周期到周期态，再由周期状态逐步转变成混沌态和超混沌态.其中控制参数k1，k2具有不同的取值范围，可为下文中硬件电路的实现和电阻调整做相应的参考，以便设计出不同运动形式的电路.

在非线性系统中，经过倍周期分岔达到混沌是一种典型的通向混沌的道路.图3为状态变量x关于参数k1，k2给出的不同分岔图，参数k1的取值范围是k1∈[-15，-5]，参数k2的取值范围是k2∈[-4，0].

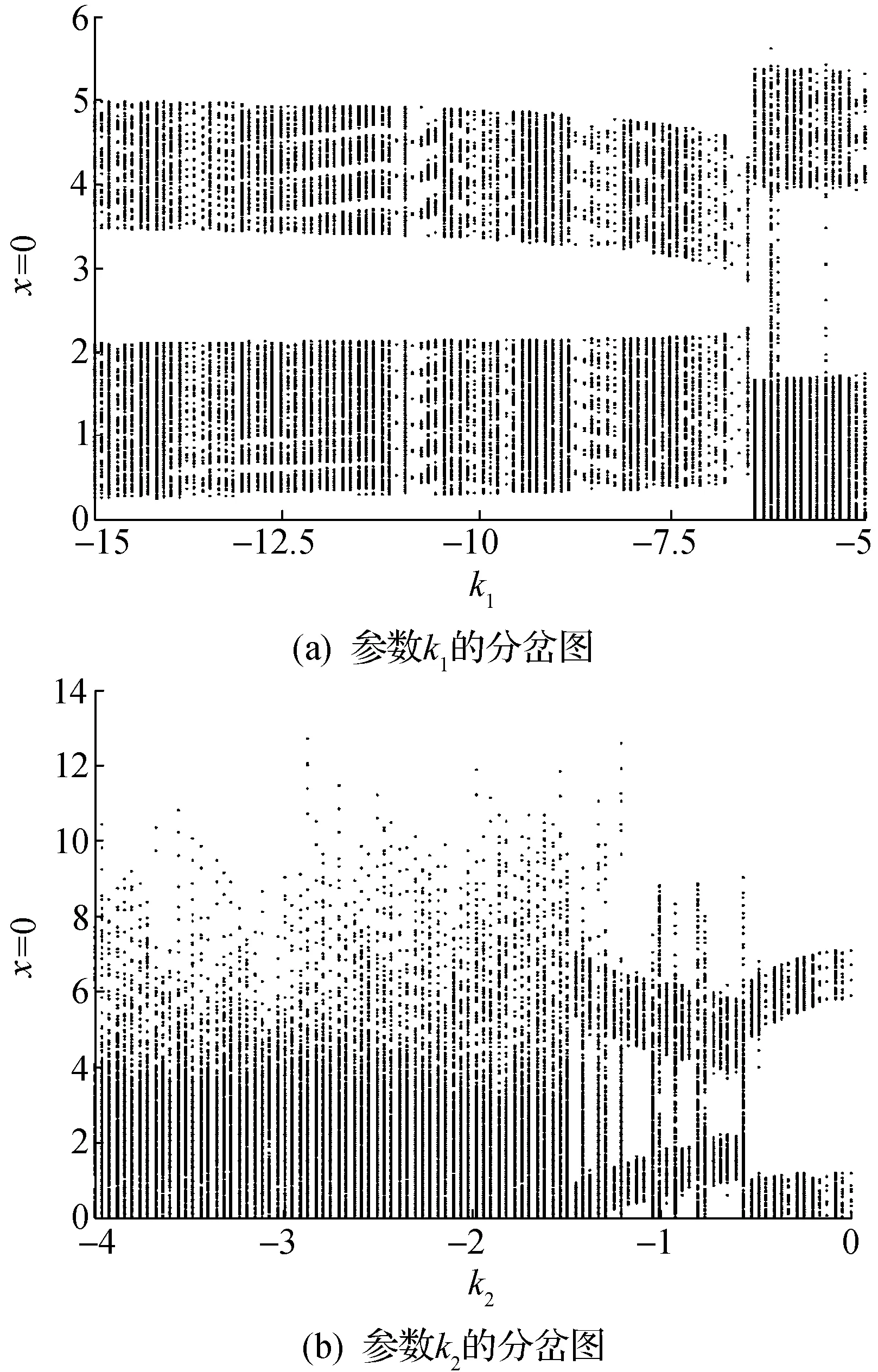
图3 式(2)的分岔图

混沌动力学系统的特性分析除了上述几个方法外，还可以通过庞加莱截面观察.选择截面适当的部分，并保证截面切线轨迹不能和吸引子相交，也不在轨道平面上.

定义2当系统的庞加莱截面是两个离散的点时，则该系统是周期性振荡；当系统的庞加莱截面有若干个离散点时，则该系统是准周期振荡；当系统的庞加莱截面是由类似线状或片状的、并具有分形特征的大量点组成时，则该系统是混沌运动.选取x=0截面，可以得到式(2)的poincare截面图，如图4所示.

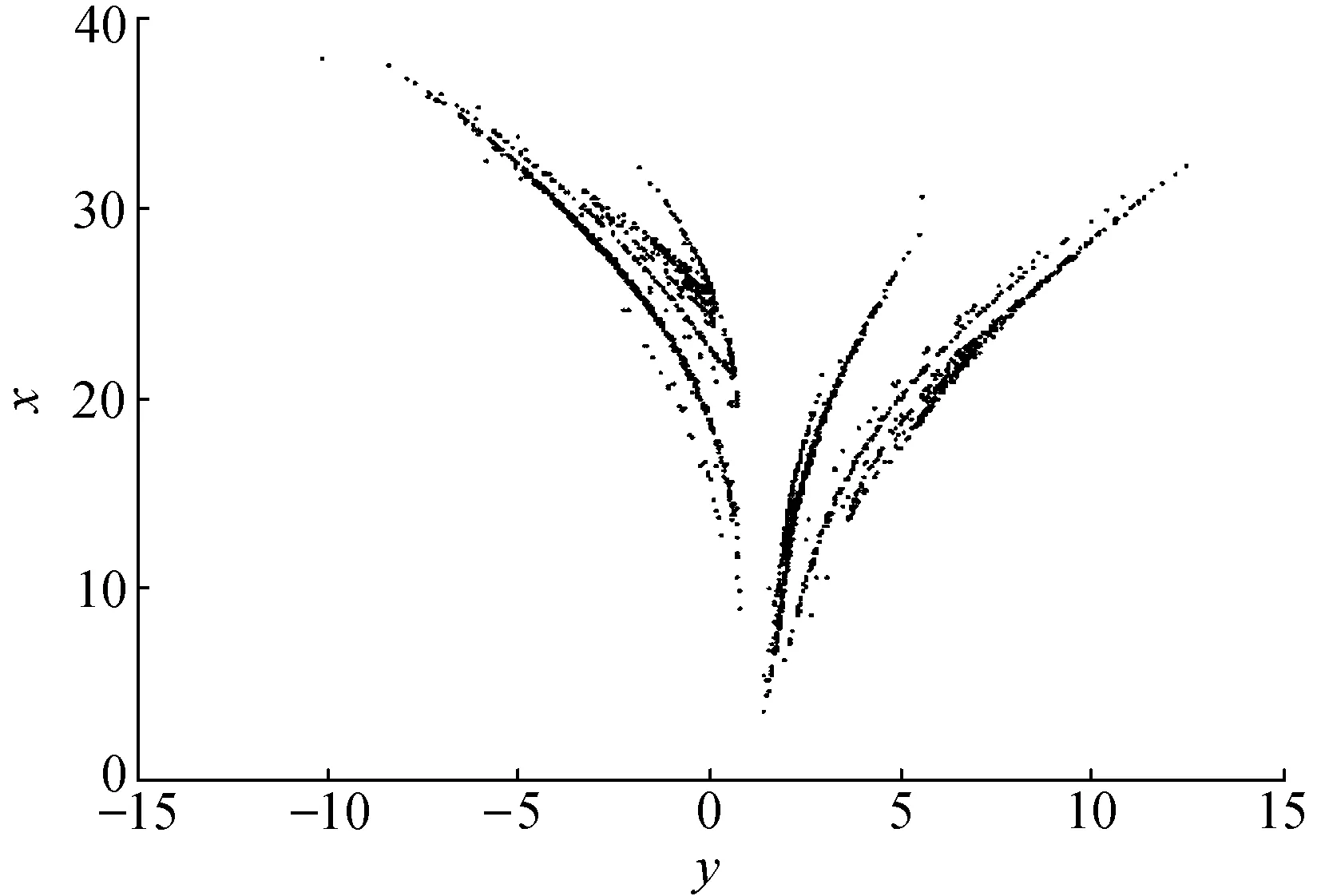
图4 式(2)中x=0时y-z的Poincare映像图

从图4可看出：x=0的截面上有一些成片的具有分形结构的密集点，同时，一些被反复折叠的叶片进一步说明了该五维系统动力行为的复杂性[21].

3 五维受控混沌系统的电路设计与实现

混沌系统的最直接最简单的物理实现是通过电路来完成的，许多混沌的动力学行为也通过电路得到了验证[22-23].为了验证这个五维受控混沌系统的动力学行为，根据式(2)在Multisim中设计实现了该系统功能的实际电路，如图5所示.电路中包括5个相互耦合的通道，分别实现状态变量x，y，z和反馈变量u，v的耦合.电路基本元件包括电阻，电容等.由于式(2)中存在多个非线性项，所以该模块主要由模拟乘法器AD633实现，其增益为0．1；电路中的模拟运算放大器LM741实现系统中的加法，减法和积分的模块，其供电电压为18 V.特别要注意的是，变量x，y，z，u，v各自的动态范围比较大，大约在102～104之间，大于运算放大器的饱和电压，故必须进行变量比例压缩变换才能电路实现.这里我们主要通过调节电路中的积分环节来实现这一压缩变换.取RC=104，等价于在确保原系统性质不变的情况下，使得输出信号的幅值提高了1 000倍，方便了图像的观察[23].

设计过程中取参数a=36，b=20，c=3，控制参数k1=-1，k2=-2，从而式(2)为

(6)

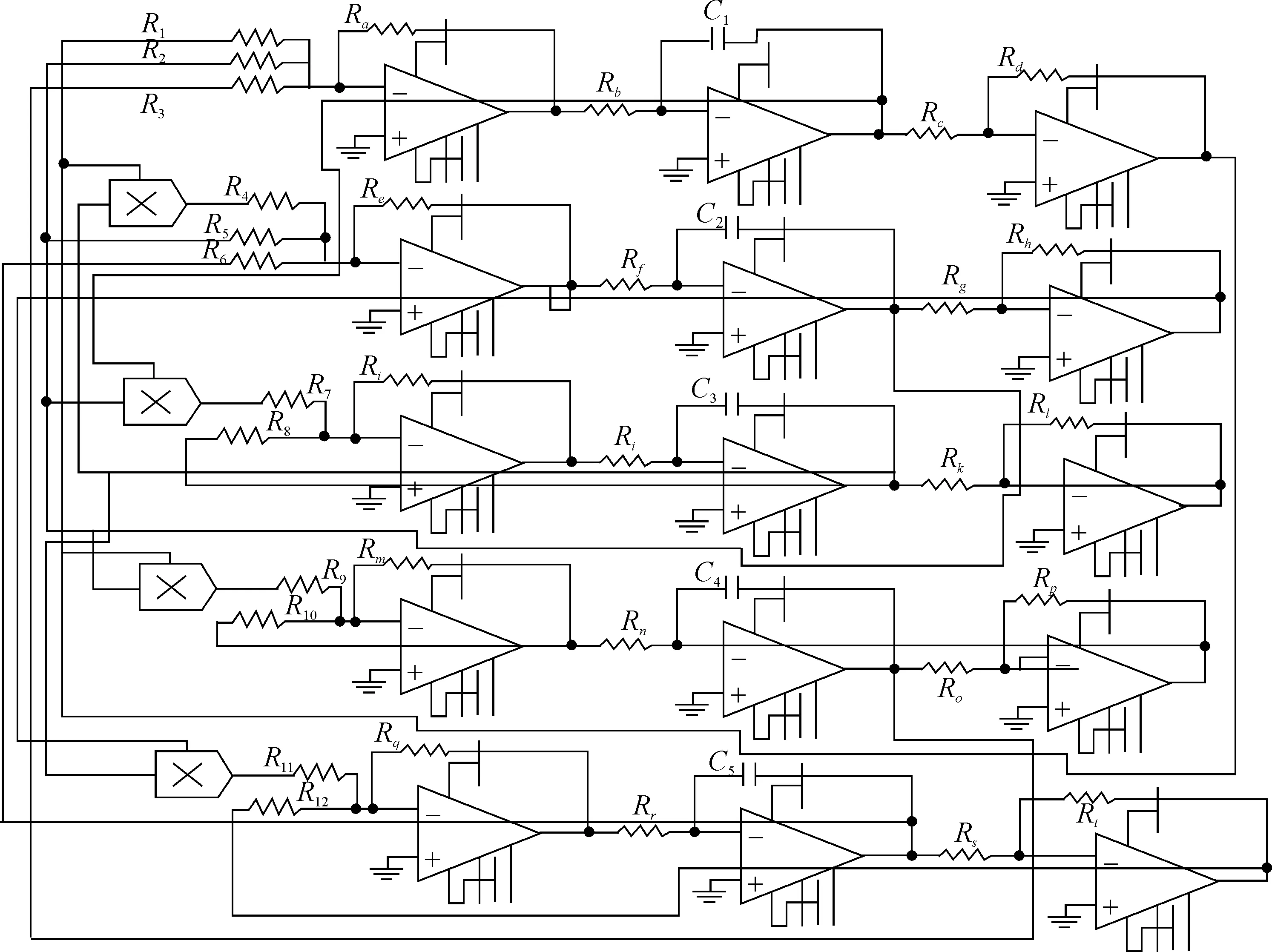
图5 式(2)的模拟实验电路原理图

根据图5得到的电路方程为

(7)

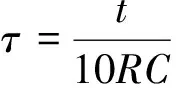
(8)

取R=Ra=Rb=Rc=Rd=Re=Rf=Rg=Rh=Ri=Rj=Rk=Rl=Rm=Rn=Ro=Rp=Rq=Rr=Rs=Rt=10 kΩ，C=C1=C2=C3=C4=10 nF.根据式(6,8)得R1=R2=2．778 kΩ，R3=R6=R10=100 kΩ，R4=R7=R9=R11=10 kΩ，R5=5 kΩ，R8=33．333 kΩ，R12=50 kΩ.

在Multisim仿真中，将模拟示波器(Agilent oscilloscope)一端接在x输出端，另一端分别接在y,z,u,v输出端进行观察该混沌系统的轨迹.然后再将一段接在u输出端，另一端接在v输出端进行模拟，结果如图6所示.

图6 式(2)模拟电路的输出相图

这些轨迹和Matlab中的数值仿真结果基本一致.由于系统处于混沌状态，其产生的序列具有非周期性，且对初值条件十分敏感，以及系统在操作运行过程中容易受到外界高频信号或随机噪声的干扰，使得模拟实验结果与仿真结果存在略微偏差.

上述电路仿真了五维受控混沌系统的混沌运动形式，根据2．4中的Lyapunov指数谱与控制参数k1，k2的关系，通过改变k1，k2的值从而改变电路中R10和R12的值即可实现其他动力学行为，鉴于篇幅原因，笔者只给出R10=100 kΩ，R12=50 kΩ时的混沌状态的相图.

4 结 论

在经典的Lü系统基础上，增加两个非线性控制器，构造了一个新的五维双受控混沌系统，通过理论分析和数值仿真，在Matlab中实现了该系统的所有动力学特性.运用Multisim搭建电路图模拟，验证了系统的正确性.观察两个控制参数与五个Lyapunov指数的关系，调整控制参数的大小就可以实现对该五维超混沌系统不同运动特性的控制.在应用电路中，两个控制参数分别与相应的一个电阻对应，改变阻值即可改变控制参数的大小，从而改变系统的运动特性，方便简单，具有普适性.由于系统运动形式及其复杂，并且拥有灵活的可调性，因此在具体的混沌保密通信中可靠的实用价值和广阔的开发前景.

本文得到了浙江工业大学人文中心项目(z20130308)的资助.

参考文献：

[1] 崔力，欧青立，徐兰霞．分数阶Lorenz超混沌系统及其电路仿真[J]．电子测量技术，2010，33(5)：13-16．

[2] 关新平，范正平，张群亮，等．连续时间稳定线性系统的混沌反控制研究[J]．物理学报，2002，51(10)：2216-2220．

[3] 陈向荣，刘崇新，王发强，等．分数阶Liu混沌系统及其电路实验的研究与控制[J]．物理学报，2008，57(3)：1416-1422．

[4] 孔德彭，孔德辉，舒露丝．基于FPGA的新型五阶超混沌吸引子的实现[J].浙江工业大学学报,2013(10):172-176.

[5] KALOSHIN D A. On the construction of the homoclinic butterfly bifurcation surface for the lorenz system[J]． Differential Equations，2013，39(11)：1648-1650．

[6] 李险峰，褚衍东，徐冬亮，等．一个新类Lorenz混沌系统的动力学分析及电路仿真[J]．四川大学学报，2008，45(5)：1168-1173．

[7] 孔德彭，杜学文，孔德辉．基于回转器变换和混沌的光图像加密[J].浙江工业大学学报，2012，40(4)：458-462.

[8] VINU V D， JANAHANLAL S， NESSY T． New results on the global chaos synchronization for Liu-Chen-Liu and Lü chaotic systems[J]．Power Electronics and Instrumentation Engineering，Communications in Computer and Information Science Volume 102,2011:20-27.

[9] 王兴元，武相军．不确定Chen系统的参数辨识与自适应同步[J]．物理学报，2006，55(2)：605-609．

[10] GAMAL M M, EMAD E M, MANSOUR E A． On the hyperchaotic complex Lü system[J]．Nonlinear Dynamics,2009,58(4):725-738.

[11] 刘明华，禹思敏．多涡卷高阶广义Jerk电路[J]．物理学报,2006,55(11):5707-5713．

[12] 禹思敏，林清华，丘水生．四维系统中多涡卷混沌与超混沌吸引子的仿真研究[J]．物理学报，2003，52(1)：25-33．

[13] 鲁池梅．基于虚拟仪器三维四翼混沌系统研究及实现[J]．电子设计工程，2010，18(4)：15-21．

[14] 罗明伟，罗小华，李华青．一类四维多翼混沌系统及其电路实现[J]．物理学报，2013，62(2)：020512．

[15] 孙克辉，任健，丘水生．分数阶统一系统的混沌动力学特性[J]．华南理工大学学报，2008，36(8)：6-10.

[16] LAN Yong-hong， ZHOU Yong. Non-fragile observer-based robust control for a class of fractional-order nonlinear systems[J]．Systems & Control Letters， 2013， 62(12)：1143-1150．

[17] 李春来，禹思敏．一个新的超混沌系统及其自适应追踪控制[J]．物理学报，2012，61(4)：040504．

[18] 周小勇．一个新混沌系统及其电路仿真[J]．物理学报，2012，64(3)：1-9．

[19] 齐爱学，王洪刚，李卫兵．开关超混沌系统及其电路实现[J]．计算机工程，2013，36(13)：205-207．

[20] 龙燕，陈帝伊，杨福增．超混沌系统的电路仿真及其自适应同步[J]．电子设计工程，2010，7(18)：63-67．

[21] 唐良瑞，李静，樊冰．一种新四维超混沌系统及其电路实现[J]．物理学报，2009，58(3)：1446-1455．

[22] 冯朝文，蔡理，康强，等．一种新的三维自治混沌系统[J]．物理学报，2011，60(3)：1-7．

[23] 仓诗建，陈增强，袁著祉．一个新四维非自治超混沌系统的分析与电路实现[J]．物理学报，2008，57(3)：1493-1500．