碰撞接触模型的理论推导与数值方法的应用

，

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

对于摩擦碰撞问题，现有的理论多讨论刚性物体的正碰撞问题.通过碰撞过程，碰撞物体的法向相对速度发生改变，而碰撞冲量与法向力方向相同.在考虑不完全弹性碰撞时，即发生塑性形变的情况，描述碰撞过程的动力学方程数目不足以确定碰撞后物体的速度等未知变量，必须增加条件才能使方程组封闭有解.Newton在1686年最早提出将碰撞前后的法向速度之比定义为恢复因数e，以此补充正碰撞问题的条件.1817年Poisson将正碰过程的恢复阶段和压缩阶段的冲量之比来定义恢复因数e，显然两种定义是一致的.而对于斜碰撞，一般仅仅关注无摩擦的理想情形.对于有摩擦的情况，Whittaker(1904年)提出了切向冲量等于法向冲量乘以库伦摩擦系数，其方向与碰撞前切向滑动速度的方向相反.1984年Kane[1]在关于双摆末端与平面碰撞的算例中发现，利用Whittaker假定的计算结果会导致碰撞后双摆的总机械能大于碰撞前的不合理的计算结果，在随后的研究工作中，人们先后对此问题产生的原因提出了一些修正方案[2-7]，然而这些方案仍有许多的局限性，且多以定性阐述为主，笔者将以理论推导的形式并配合数值计算方法来探讨研究这一问题.

1 球与弹性半空间碰撞接触模型物理量计算

以一个小球与弹性平面发生斜碰撞为研究对象，球的半径为R，密度为ρ，质量为m，球以初速度v0，角速度ω0，沿跟z轴负向呈α夹角与弹性半空间表面发生碰撞，球质心为O，球与半空间表面接触部分的最低点为P，半空间与P接触的点为Q.其中，角速度方向以图示逆时针方向为正，速度方向以座标轴正向为正.须说明的是，P和Q两点不是物体上的固定点，而是在P和Q这两个位置上的点，两者接触面半径为a.设接触面任意一点的法向位移为uz，到接触中心的水平距离为r，接触面最低点的压力为p0，球压入半空间的最大深度为d(图1).

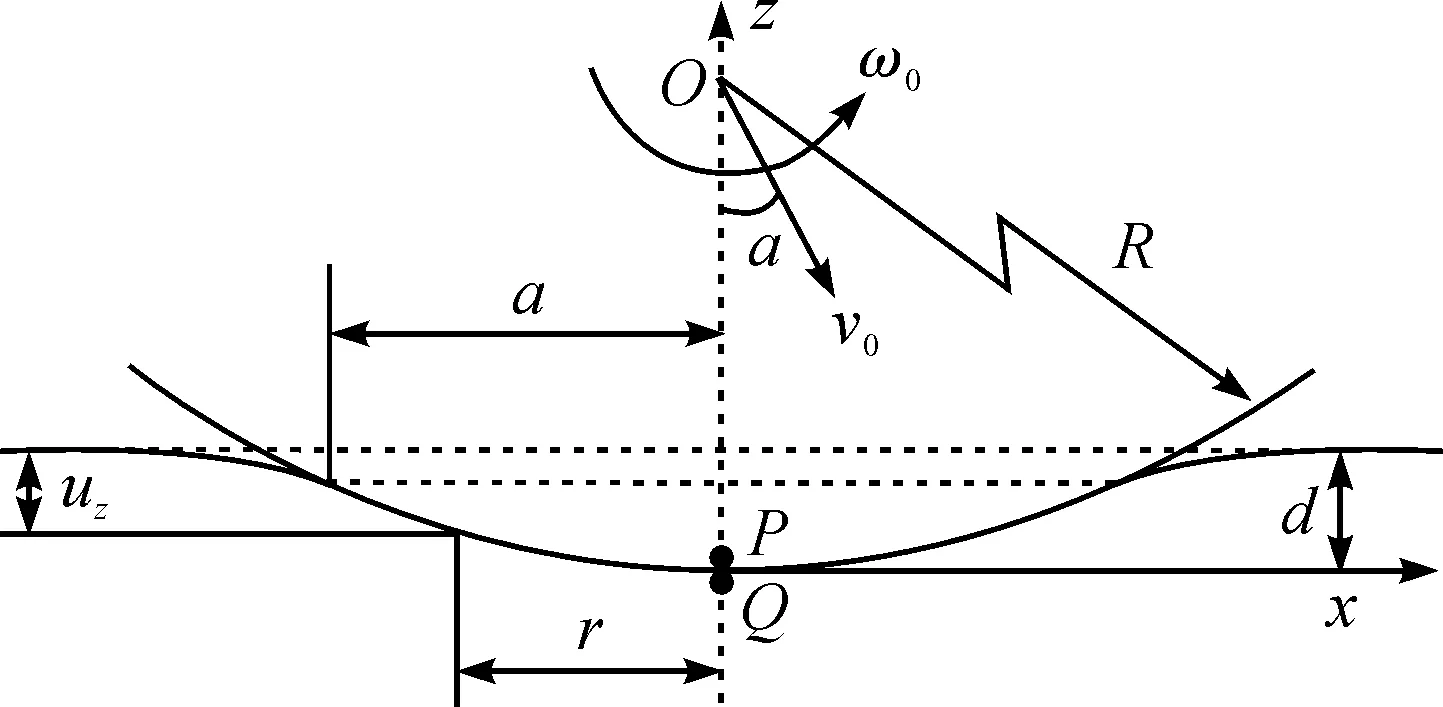
图1 球与平面接触碰撞模型

对于刚性球与弹性半空间的接触碰撞模型，根据弹性理论[8]知当弹性半空间上一点分别受法向集中力和切向集中力作用时，在弹性半空间表面处沿z和x方向的位移分别为

(1)

其中：E为弹性半空间弹性模量；μ为泊松比；r=(x2+y2)1/2；G=E/[2(1+μ)]；Fz和F分别为沿接触面法向和切向的集中力，接触面上的法向应力分布为

(2)

为计算接触面上的压入深度，建立图2所示的接触积分区域，有

t2=(ssinφ)2+(r+scosφ)2=r2+s2+2rscosφ

(3)

将式(3)代入式(2)，有

(4)

令α2=α2-r2，β2=rcosφ，有

(5)

因接触圆边界上压力为零，设s0为方程α2-s2-2βs=0的正根，得接触圆域的积分上限为

(6)

对式(1)中的uz在接触圆域进行积分，有

(7)

由于积分的对称性，β的一次项在φ∈[0,2π]上积分为0，则得接触面法向位移为

(8)

其中：E*=E/(1-μ2)；r=(x02+y02)1/2且r≤a.

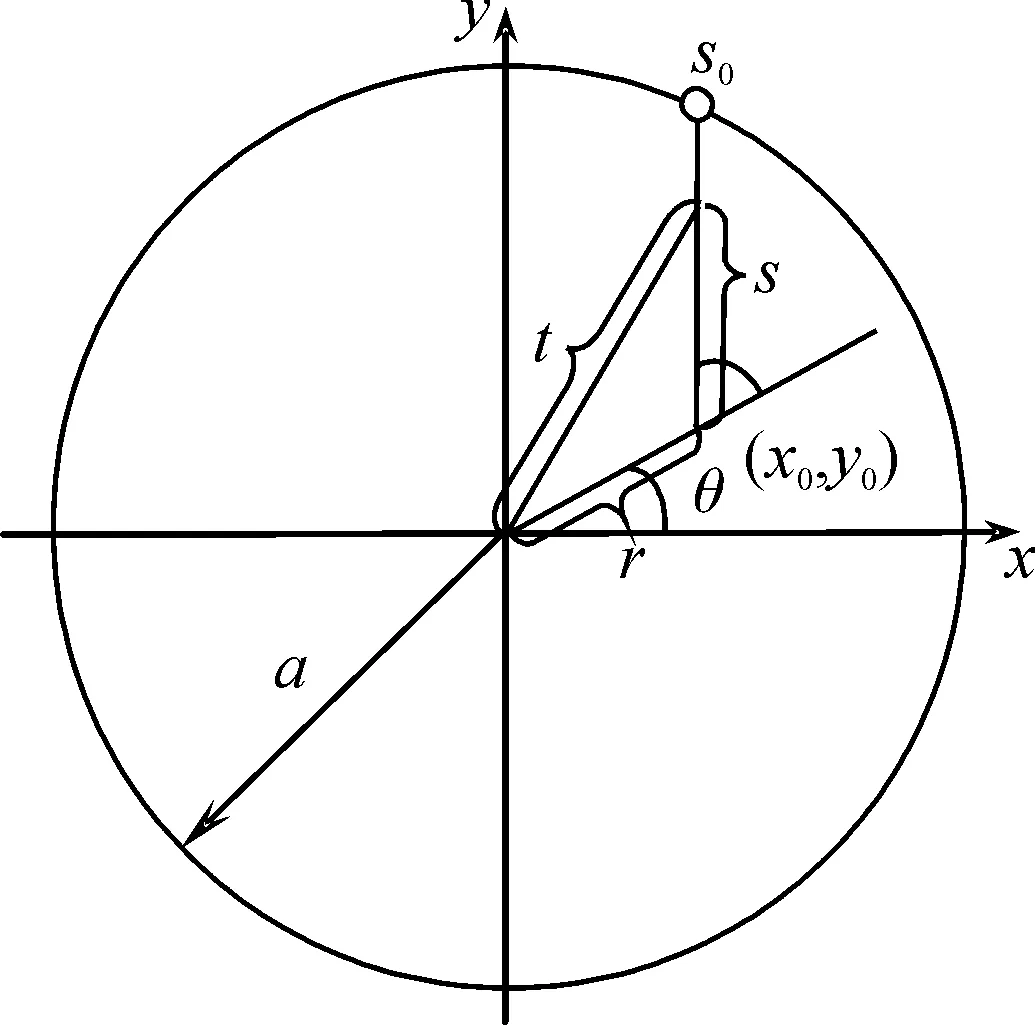
图2 接触积分区域

同理，对于切向分布力

(9)

将式(3)代入式(9)，并令α2=α2-r2和β2=rcosφ，有

(10)

对式(1)中的ux在接触圆域进行积分，并考虑到积分的对称性，得到接触面上的切向位移为

(11)

其中：x0=rcosθ；y0=rsinθ.当x0≪a时，ux(x0,y0)≈ux(0,0)，可忽略后两项.并且当x0和y0都为0时，有最大切向变形，以其为考察点写为

(12)

将式(2，9)分别在接触面上积分可得球对平面的法向力和切向力，即

(13)

(14)

由FN=∂UN/∂d和FT=∂UT/∂uQx，分别对d和uQx进行积分，可得弹性半空间的应变能近似为法向应变能与切向应变能之和，可写为

(15)

根据牛顿第二定律可得接触面上压入深度d的微分方程

(16)

其中：KN=4E*R1/2/(3m)，考虑到球的运动，则d，uQx，p0，a都为时间的函数.

球的动能为平动动能与转动动能之和，写为

(17)

其中：vOx为球质心速度在x方向的分量；vOz为球质心速度z方向的分量；J为球的转动惯量，其值为2mR2/5；ω为球自转的角速度.

摩擦损耗的能量是由球与半空间表面接触位置的相对运动产生的，计Q点沿x方向的速度为vQx，球最低点P相对于Q点的速度为vr，有

vr(t)=vOx(t)+Rω(t)-vQx(t)

(18)

(19)

其中vr的方向以座标轴正向为正.

球与弹性半空间组成一个系统，根据能量守恒定律，系统总能量为上述三部分能量之和且应为常数，其值等于球的初始动能.并且，弹性半空间的应变能与摩擦损耗的能量都不小于零.于是球与半空间碰撞后的动能不应大于其初始动能，即E1(t)≤E1(0).若不满足这一条件，则有悖于能量守恒定律.

2 数值离散

对于式(16)给出的d(t)的微分方程很难得到其解析解，但故而采用数值方法进行近似计算.设Δt为很短的一段时间，由中心差分法可以得到d(t)的二阶差分式

(20)

于是，将d(t)离散成n个时刻的值，相邻时刻的时间间隔均为h，即h为时间步长，得到离散形式为

(21)

球刚刚接触到弹性半空间时记为0时刻，此时的最大压入深度d(1)=0，球与半空间没有相互作用力，近似认为d(2)=-hvOz.在h较小的时候可以较精确地得到d的近似值.

球心法向速度的正方向与压入深度相反，其大小等于d(t)的一阶导数，由中心差分法得

(22)

将其离散得

(23)

发生动摩擦时，令摩擦力方向与P和Q相对速度方向相反，按库伦摩擦定律可得球对弹性半空间表面切向力FT的离散形式

(24)

由式(14)可得

(25)

在较短的时间间隔内，将FT(t)近似视为随时间呈线性变化，根据冲量定理可得

(26)

将其离散得

(27)

同理，对于角速度ω(t)有

(28)

将其离散得

(29)

Q点速度为Q点位移的一阶导数，由中心差分法可知

(30)

将其离散得

(31)

于是可以得到相对速度的离散形式

vr=vOx+Rω-vQx

(32)

再根据式(15，17，19)得到能量的离散形式，设i为正整数，从2～(n-1)变化时，有

(33)

(34)

(35)

在先得出d数值解的基础上，由离散公式计算刚性球与弹性半空间碰撞过程中各个物理量的近似值.在静摩擦情况下，Q点随P点运动，而切向力应由Q点位移确定，同时切向力影响着P点的运动速度，在此复杂的耦合状态下，可用增量法得到近似的解.在变力条件下，对球心O点，可设

(36)

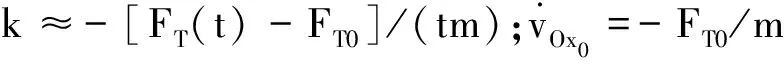
(37)

(38)

同理可得，P点由角速度产生的位移为

(39)

其中：k1≈-[FT(t)-FT0]R/(tJ)；角加速度β0=-FT0R/J.当t→0时，uOx(t)和uω(t)能取到比较精确的值.此时忽略t的三次项，得到Q点位移的增量式，将其离散得

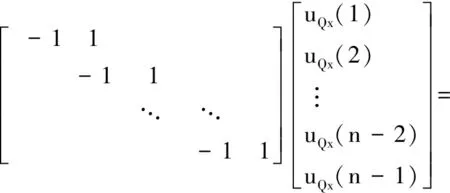
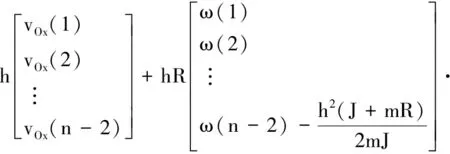
(40)

切向力的离散形式为

(41)

此时不发生动摩擦，P和Q相对速度为零，无摩擦损耗.要注意的是，动静摩擦之间的变换可能发生于离散后的两个相邻时刻之间，对此可用插值法修正来得到更接近实际情况的结果.

3 结 论

刚性球与弹性半空间发生带有摩擦的斜碰撞问题，会出现物体机械能增大这一与能量守恒定律相悖的现象，笔者在研究中采用了解析的方法推导出碰撞接触点处位移的微分方程，并通过数值方法求解这种二阶非常规的微分方程，对于各物理量同时进行了数值离散，这种方法为发现系统能量不守恒的原因提供了一种可行的解决途径，由于篇幅所限，具体的计算结果将另文发表.

参考文献：

[1] KANE T R, LEVINSON D A. Dynamics, theory and applications[M]. New York: McGraw-Hill,1985.

[2] KELLER J B. Impact with Fiction[J]. ASME J Applied Mechanics,1986,53:1-4.

[3] BRACH R M. Rigid body collisions[J]. ASME J Applied Mechanics,1989,56:133-138.

[4] SMITH C E. Predicting rebounds using rigid-body dynamics[J]. ASME J Applied Mechanics,1991,58:754-758.

[5] 刘延柱.刚性椭球对固定面的三维摩擦碰撞[J].力学学报，1997，29(6)：726-732.

[6] 刘延柱.关于摩擦碰撞的Kane难题[J].力学与实践,2012,34(1):91-94.

[7] 刘延柱.再论Kane难题[J].力学与实践，2013，35(3)：77-79.

[8] 徐芝纶.弹性力学[M].3版.北京：高等教育出版社,1978.