脑血管计算机模型的建立与有限元分析

，，

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

血管疾病已成为当前发达国家威胁公众健康的头号因素，促使科学家和研究学者对此做了大量研究，并取得了一定成效，但如何更好理解血管形态结构以及血管疾病的生成等许多问题仍然是开放研究的[1].CT和MRI在各种脑血管疾病的诊治中发挥了重要作用.MRI检测海绵状血管瘤相当成功，CT血管造影在检测脑发育性静脉异常非常出色[2]，这使得实际应用中，往往是两种或与传统的造影相结合的检查方式.CT因为血管与周围软组织的灰度相似性[3]，通常要采用较为复杂的分割技术才能得到较好分割结果.磁共振成像(MRI)检查因不受病变部位限制，图像分辨率高，可同时对血管几何形态、血管壁特征及血流速度进行无创性测量等，在对动脉血流动力学状态进行评估方面应用前景良好.针对不同病变的脑血管图像，选取两组MRI磁共振数据建立模型，完成对断层数据的三维分割和体绘制、感兴趣域重建，得到有效的几何模型，最后进行流体动力学模型分析.整个模拟过程是基于一套商业CFD软件包，使得方法最终能够为医生掌握和操作.

1 几何模型重建

MITK是由中国科学院自动化研究所开发，它是整合了VTK和ITK的—套综合医学图像处理工具包[4].这个工具包实现了医学图像分割、配准和可视化等基本功能，有着统一的编程接口、使得复用性与灵活性得到较大提高.该研究所每年对工具包不定期更新，使其充分满足科研需求.

实验在VS2008编译环境下，基于MITK平台实现了血管的体绘制三维重建，显示效果较好，克服了血管内图像亮度变化小、形状不明显以及图像分割效果不好的局限.采用等值面模型和光线体绘制算法实现了血管三维绘制，并对模型进行阀值分割、任意平面裁剪、表面绘制等交互操作，可以直观、定量地对血管内部结构进行察看.

1.1 阀值分割

整个实验分为建模和模拟两部分.建模实验的输入为标准DICOM3.0格式的医学图像文件，经过阀值分割和感兴趣区域提取、表面重建处理，输出为STL格式模型文件，建模流程如图1所示.

图1 建模方法

当前流行的图像分割方法中，主要是基于区域的分割、基于边缘分割和基于两者的混合方法.基于区域的分割如下面要采用的阀值分割；基于边缘的分割一直是研究的热点，例如Snake模型，有许多学者对此方法进行了研究和方法改进[5].考虑MRI体数据特点，首先利用阀值分割方法对三维数据进行分割.设原始图像为f(x,y,z)，按照准则设置的阀值t1和t2将图像分为两部分，分割后的图像为

(1)

即像素值在低阀值和高阀值之间保留原值f(x,y,z)，其他的值为零(图2).

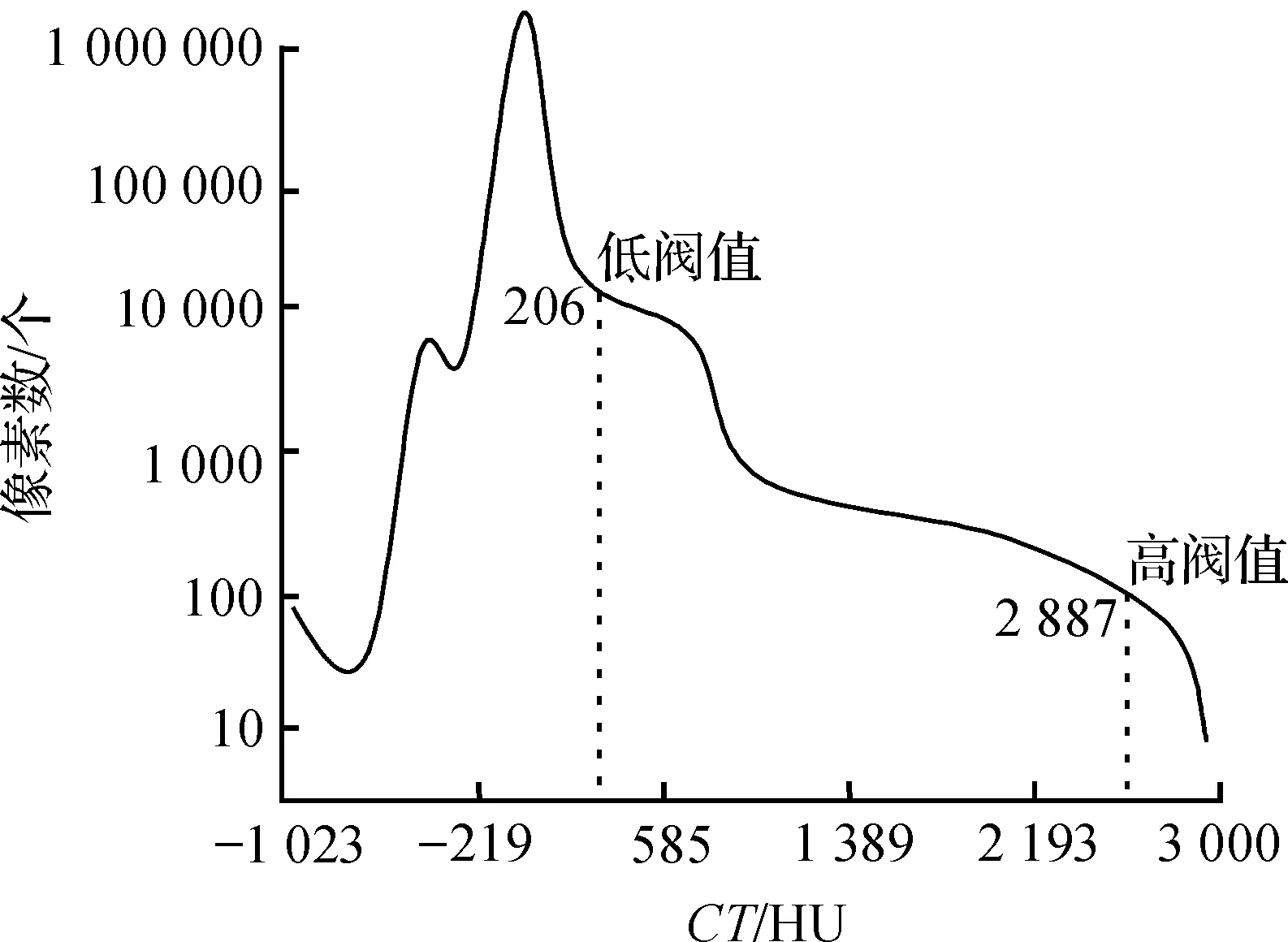
图2 双阀值分割直方图

1.2 体绘制和感兴趣区域裁减

体绘制指直接基于三维体数据进行绘制的方法.三维数据场的显示与体数据定义的空间函数在整条光线上的取值相关，是由具体的体绘制模型和计算方法决定的.主要的体绘制模型有等值面模型、最大密度投影(MIP)、颗粒模型等.不同的绘制算法对问题逼近的效果也会不同.典型的算法分图像空间的算法和物体空间的算法两大类，其中以图像空间算法——光线投射法为研究热门.对于光线投射人们提出了很多优化的算法，特别是利用不同的硬件为算法加速的技术，使其成为体绘制的标准和主流.利用MITK平台设计的交互剪切工具，从原始三维图像数据中获取部分感兴趣分支(图3).

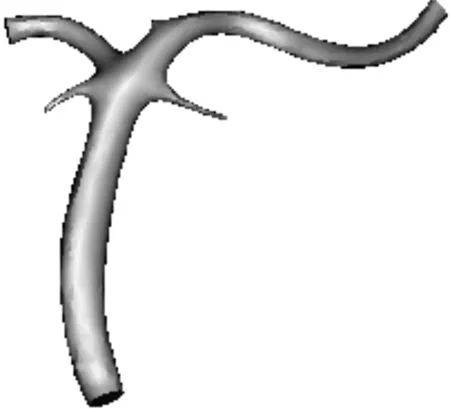
图3 感兴趣区域

1.3 分割基础上的表面提取与面绘制

建立模型的最终目的是要提取可用于模型计算的三角面，因此需要提取模型表面模型.通过Marching Cubes算法可以从三维的数据场中抽取出等值面.Marching Cubes是一种经典的医学图像三维重建算法,近年来随着医学图像处理技术的发展，众学者提出了许多改进方法[6].实验取经验阀值(100,255)作为Marching Cubes算法的两个参数提取出等值面的三角网格面表达.Marching Cubes算法处理过的模型已经是三角片表面模型，但只是知道每个等值点的坐标，需要计算每个等值点的法向量，以进行真实感绘制，可以使表面更加平坦，有利于后续化简过程.中点选择公式为

P=(P1+P2)/2

N=(N1+N2)/2

(2)

其中：P为等值点坐标；P1,P2分别为两端点的坐标；N1,N2分别为两个端点的法向量.这样重建出来的图像可能还是不光滑的，需要进行平滑和数量上的优化.

2 有限元分析

在实验的CFD模拟部分应用的是商业软件(ANSYS ICEM CFD和ANSYS FLUENT)，因此所有操作对于一般医生的日常操作均是可操作的.

2.1 网格划分

表面模型以STL格式导入ICEM CFD，以创建适合流体计算的高质量网格.虽然Delaunay三角剖分有着简单、快速等优点[7]在数值分析应用较多，但八叉树网格密度比较容易控制，剖分速度也比较快.在划分方法中采用八叉树算法建立了两组数据模型，第一组图是正常人体的局部动脉几何模型，第二组是明显动脉瘤的局部动脉几何模型，如图4所示.对两组数据进行网格划分的结果，见表1网格的相关特性统计.

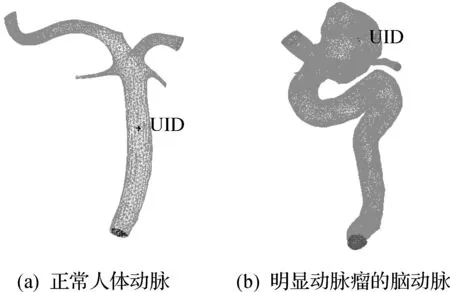
图4 八叉树网格模型

表1 划分后八叉树网格参数

2.2 有限元仿真

本实验将血管壁和瘤壁设为刚性壁边界，动脉瘤壁厚度一致.其中求解器选择pressure-based求解器；湍流模型选择k-epsilon湍流模型；材料属性定义流体类型为血液，其密度为1 050 kg/m3，粘性为0.004 kg/(m2·s)；边界条件设定入口速度为0.4 m/s；入口压力设为9 332 Pa；迭代300次计算.得到两组结果：第一组图是正常人体的动脉血管矢量分布，第二组是明显动脉瘤的血液矢量分布.

需要注意的是，实验假设血管壁为刚性一致厚度薄壁，刚性壁会比实际获得的应力要大得多，但一致的厚度假设相当于把瘤壁厚度(特别是易破裂的部分)变厚了，会减小其机械应力.因此，实际运用中各有采用，弹性壁的例子见文献[8].

血管壁切应力(WSS)是指血液流动时对血管壁产生的切向应力，是一项重要的血管壁力学参数，在多种血管病变发生过程中发挥重要作用.血管壁的切应力或震荡切应力被指与斑块易损性及斑块破裂密切相关.一般认为，血管内异常的血流模式，如扰动和湍流，在斑块形成和发展过程中也起到重要作用.

由图5所示，在分叉部位形成血流分离区，局部存在低血流、低WSS，分叉下游区出现高振荡切应力区域并有次级血流模式形成，这和以往血流动力学研究是一致的.图6中除了与第一组正常人体相似的血流特征外，还有一些自己的特点：比较大的WSS出现在动脉瘤的根部，一般称为动脉瘤颈；同样，在动脉瘤根部附近的血液流速和湍流明显高于其他部位.

图5 正常人体的动脉血管矢量分布

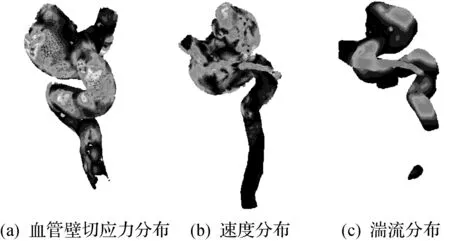
图6 有明显动脉瘤的动脉血管矢量分布

3 结 论

据统计，有限元模型的建立及前处理要占CAE软件分析流程80%的时间[9]，因此研究建立简便而精确的颅内动脉瘤三维有限元模型非常必要.计算机技术的发展使得有限元分析方法能够应用于生物力学领域中，但是人脑动脉因其血管树复杂，建立脑动脉血管的有限元计算模型依然是进行动脉瘤分析问题过程中面临的难题.针对这种困难，采用MRI扫描数据直接应用进行分割和建模，没有利用其他中间软件，大大减轻了工作量，极大地提高了建模的速度，获得的脑动脉几何模型为随后的有限元分析建立了基础.通过有限元分析软件的前处理器建立了与颅内动脉实际状态相近的有限元计算模型，对所建的脑血管有限元动力流体动力学分析，得到与试验大致相符的矢量图，从而使所建的有限元模型得到了充分的验证.同时，实验得到局部血管内各部位的血液流速、压力和扰动和湍流等参数变化，为研究颅内动脉瘤提供了重要的参考.有限的硬件资源下成功完成了复杂的脑动脉瘤建模和有限元分析，实验具备经济性，整个流程清晰简洁，具有可操作性.

参考文献：

[1] SANTAMORE W P, BOVE A A. Why are arteries the size they are?[J]. Journal of Applied Physiology,2008,104(5):1259-1259.

[2] MOHAMMADI J. Imaging features of cerebral vascular malformations[J]. Journal of Medical Imaging and Radiation Sciences,2013，44(2)：71-78.

[3] 凌华强,龙胜春,项鹏远.主动形体模型法在肝脏CT图像分割中的应用[J].浙江工业大学学报,2012,40(4):450-453.

[4] 田捷,薛健,戴亚康.医学影像算法设计与平台构建[M].北京：清华大学出版社,2007.

[5] 冯晓斐,郑河荣.基于改进Snake模型与Kalman滤波的目标跟踪算法[J].浙江工业大学学报,2010,38(2):168-172.

[6] 钱峰,马秀丽,杨胜齐,等.移动立方体算法的研究和改进[J].计算机工程与应用,2010,46(34):177-180.

[7] 马培良,丁维龙,古辉.基于OpenGL和双三次贝塞尔曲面的稻叶可视化建模[J].浙江工业大学学报,2010,38(1):36-40.

[8] CHEN J, WANG S, DING G, et al. Patient-specific blood dynamic simulations in assessing endovascular occlusion of intracranial aneurysms[J]. Journal of Hydrodynamics, Series B,2009,21(2):271-276.

[9] 傅栋,靳安民.应用CT断层图像快速构建人体骨骼有限元几何模型的方法[J].中国组织工程研究与临床康复,2007,11(9):1620-1623.