面向节能的无线多传感器H∞融合估计

,,

(浙江工业大学 信息工程学院，浙江 杭州 310023)

无线传感器网络(Wireless sensor network，WSN)是一种部署在监测区域内由大量传感器构成的自组织网络，它通过多传感器融合估计来精确提取监测对象信息.WSN在军事应用、环境监测、精准农业、医疗卫生、制造业、智能楼宇、交通运输、城市管理、灾难预警与救助等诸多领域都具有广泛的应用前景[1-3].在WSN中，密集分布的传感器节点采集监测对象信息并传输给固定的融合中心(如汇聚节点)其领域内的融合节点进行融合估计，需要大量节点间的数据传输.一般情况下，WSN节点由电池供电，而且在多数应用场景下，一旦网络部署完成，很难给节点补给能量，而且研究表明的数据传输是消耗节点能量的主要因素[4-5].通过降低传感器节点间的通信量可以达到节能的目的，但同时会降低融合估计所能达到的估计性能.因此，如何权衡融合估计性能和节点能量消耗之间的关系，设计出具有能量约束的融合估计器具有一定的难度.这个问题在过去几10年吸引了许多学者的研究，主要有两种方法来解决这个问题：量化方法[5-6]和维数压缩方法[7-8].它们的主要思想是通过量化和降维，用较少的比特数表示测量信号，减少内容字段在数据包中占用的位数，从而减小包长和通信量来实现节能.但是在对一些动态系统进行融合估计时往往需要对多维信号进行处理，而对多维信号的直接量化是非常困难的.此外，维数压缩方法不能保证系统降维以后都是可观的，从而使得此种方法对某些系统不适用.

研究了一类WSN环境下能量受限的多传感器H∞融合估计问题.传感器节点采用一种新的节能传输策略，降低节点到融合中心的信息发送频率，减少节点与融合中心的通信量，从而减少传感器节点能量消耗.节能传输策略是先将传感器节点分为若干组，每组节点都按固定的传输周期(采样周期的整数倍)进行信息的传输，不同的组交替将信息传输到融合中心.从而将融合估计系统建模为一类离散时间周期系统.进而利用李雅普诺夫理论和LMI技术，并结合周期系统方法[9]，给出了滤波误差周期系统渐近稳定并满足给定H∞性能的一个充分条件和H∞融合估计器的设计方法.最后通过一个仿真算例验证所提方法的有效性.

1 问题描述

考虑如图1所示的WSN环境下的多传感器融合估计问题，假设目标轨迹和量测方程由以下状态空间模型描述，即

(1)

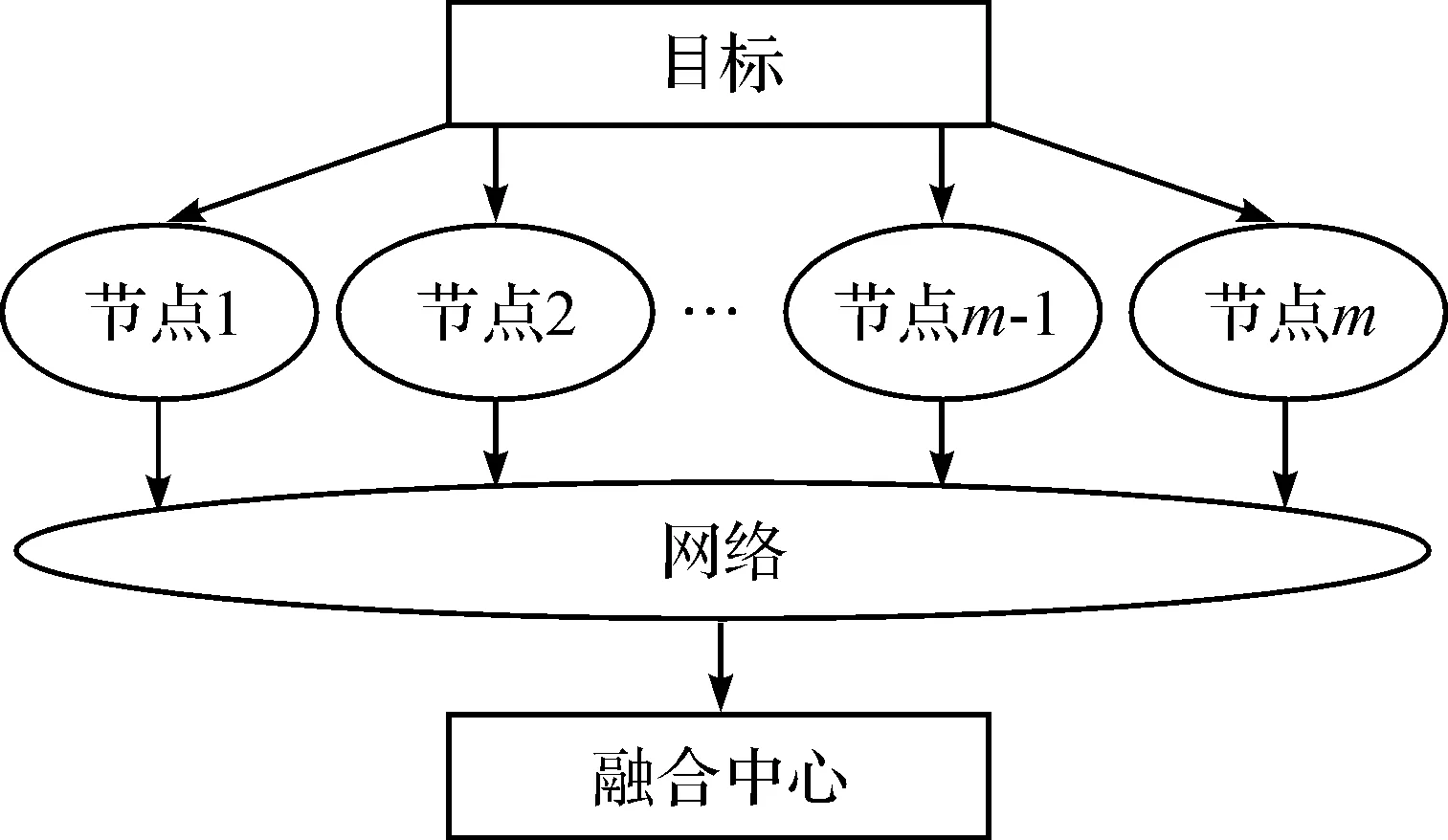
图1 WSN环境下的多传感器融合估计系统

其中：x(k)∈Rn为状态向量；yi(k)∈Rli(i=1,2,…,m)为测量输出；ω(k)∈Rp,υi(k)∈Rli分别为能量有界的模型噪声和测量噪声；A,B,ci为适当维数的矩阵和向量.待估计的信号可描述为

z(k)=Lx(k),L∈Rl·n

(2)

WSN环境下的融合估计算法必须考虑能量受限的问题，提出了一种节能传输策略，通过采用减少传感器节点信息发送频率的方法来减少节点能量消耗.具体实现方法如下：对m个传感器节点从1到m标号，定义节点集s{s1,…,si,…,sm}和，将所有节点分成了互不相关的N(N≤m)组，则节点集s和(=1,2,…,N)满足

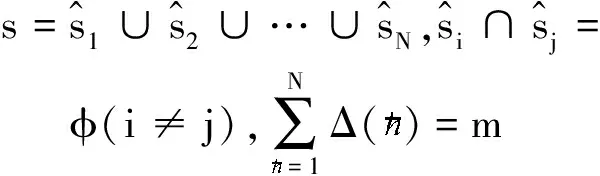
(3)

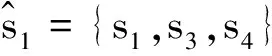
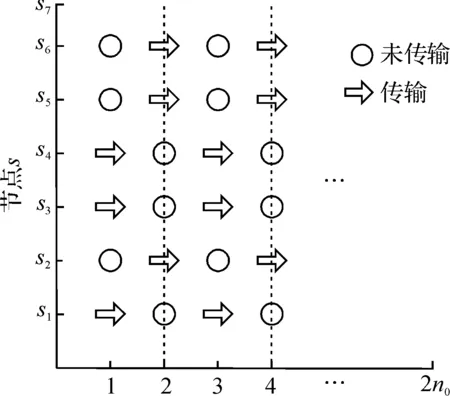
时刻k/s

注1设一个节点在某一时刻传输一次信息所消耗的能量为a，那么所有节点都传输信息所消耗的能量Ec=ma，而节能传输策略下节点平均每一时刻所消耗的能量为

(4)

式(4)在节能传输策略下，N越大，节点在传输过程中所消耗的能量越少.

(5)

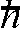
(6)

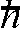
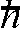
(7)

类似于文献[10]中的补偿策略，由式(5，6)可得

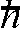
(8)

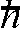
其中：diag{·}为对角矩阵；Im为m×m的单位矩阵.由式(7，8)可得

ye(k)=Π(k)y(k)+R(Im-Π(k))ye(k-1)

(9)

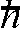
(10)

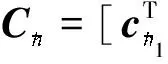
(11)

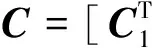
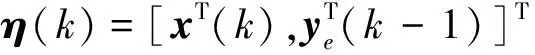
(12)

其中

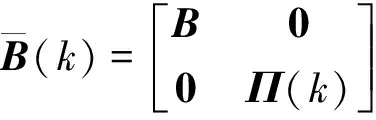
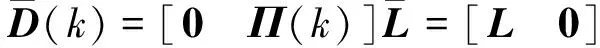
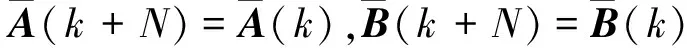
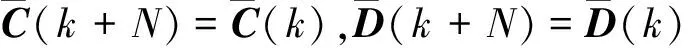
针对式(12)，考虑降阶融合估计器，即

(13)

其中：xf(k)和zf(k)分别为x(k)和z(k)的估计；Af(k)，Bf(k)，Cf(k)，Df(k)分别为待设计的估计器参数，且它们满足周期N.

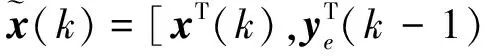
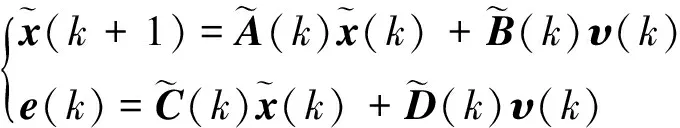
(14)

其中

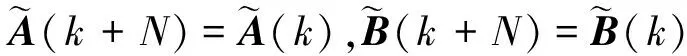
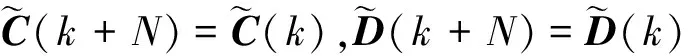
要解决的H∞融合估计问题描述如下：对于给定标量γ>0，设计如式(13)的融合估计器使得式(14)渐近稳定，并满足

(15)

2 主要结果

定理1对给定标量γ>0，若存在周期为N的对称正定矩阵序列{P(k)}k≥0(P(k)=P(k+N))，使得矩阵不等式

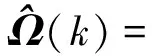
(16)

成立，则式(14)渐近稳定且具有给定的H∞性能γ.

证明当式(14)的外部扰动υ(k)≡0时，选取Lyapunov函数为

(17)

其中P(k)=P(k+N).那么

(18)

利用Schur补引理[11]，由式(16)可得

(19)

以下证明式(14)具有H∞性能γ.首先考虑性能指标为

(20)

然后在零初始状态及系统渐近稳定性的条件下，由式(14，20)可得

(21)

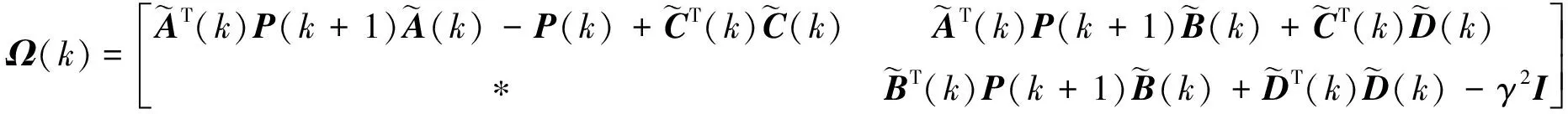
由Schur补引理知，Ω(k)<0等价于

(22)

对式(22)分别左乘和右乘diag{P(k+1),I,I,I}可得式(16).因此，如果式(16)成立，那么Ω(k)<0，即J(T)<0，令T→∞从而可得式(15)成立，那么融合估计误差周期系统(14)渐近稳定且具有给定的H∞性能γ.证毕.

考虑到式(16)不是线性矩阵不等式，故很难用定理1直接求得融合估计器的参数矩阵，为此需将式(16)转化为线性矩阵不等式来求解.

定理2给定标量γ>0，如果存在周期为N的矩阵P1(k),P2(k),P3(k),P4(k),P5(k),P6(k),Z1(k),Z2(k),Z3(k),Z4(k),Z5(k),Z6(k),Z7(k),ZA(k),ZB(k),Cf(k),Df(k)使得式(23，24)成立，即

(23)

(24)

式中：

Γ(k)=Im-Π(k)，那么式(14)渐近稳定且具有给定的H∞性能γ.且相应的融合估计器参数矩阵Cf(k)和Df(k)可直接由式(24)求得，Af(k)和Bf(k)计算式分别为

(25)

证明如果存在P(k)>0(P(k)=P(k+N))和Z(k)(Z(k)=Z(k+N))满足不等式

(26)

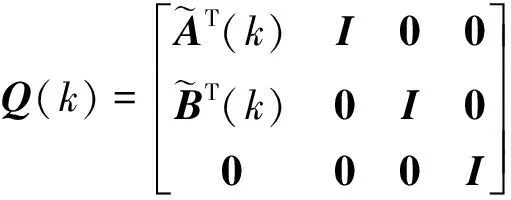
(27)

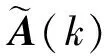
(28)

并定义矩阵变量ZB(k)Z3(k)Bf(k),ZA(k)Z3(k)Af(k).由式(27，28)通过矩阵运算可得式(24).因此，若式(23，24)成立，则式(16)成立，根据定理1，式(14)渐近稳定且具有给定的H∞性能γ，且相应的融合估计器参数矩阵Cf(k)和Df(k)可直接由式(24)求得，Af(k)和Bf(k)由式(25)计算.证毕.

注2注意到LMIs式(23，24)关于矩阵变量和标量γ2都是线性的，因此可以通过求解以下优化问题来设计最优H∞融合估计器，即

(29)

3 仿真算例

考虑具有如下系统参数矩阵的线性离散系统[12],即

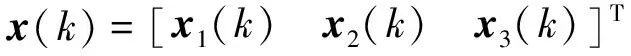
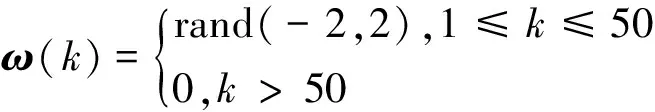
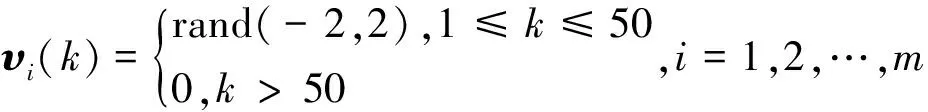
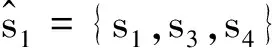
故所设计的估计器能很好的估计目标信息，验证了定理2方法的有效性.

另外，分别选取不同的传输周期N，即

对于不同的传输周期N分别求解最优问题式(29)，最优H∞性能γ*由表1给出.由表1可知最优H∞性能随N增大而变差，由式(4)可知节点能量消耗随N增大而减少.因此在实际应用中,我们可以通过权衡融合估计性能和节点能量消耗来选取出最佳的传输周期N.

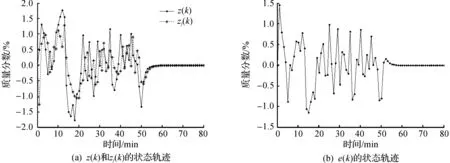
图3 z(k)和zf(k)的状态轨迹及e(k)的状态轨迹

表1 周期N和最优H∞性能γ*之间的关系

4 结 论

研究了一类WSNs环境下具有能量约束的无线多传感器系统H∞融合估计问题，通过采用所提出的节能传输策略，降低节点到融合中心的信息发送频率，从而将融合估计系统建模成一类离散时间周期系统.进而，基于融合估计误差周期系统，导出了能量受限情况下的融合估计误差周期系统渐近稳定且具有给定H∞性能的一个充分条件，并给出了H∞融合估计器的设计方法.最后的仿真算例验证了所提方法的有效性.

参考文献：

[1] YICK J, MUKHERJEE B, GHOSAL D. Wireless sensor network survey[J]. Computer Networks,2008,52(12):2292-2330.

[2] BURRELL J, BROOKE T, BECKWITH R. Sensor networks in agricultural production[J]. IEEE Pervasive Computing,2004,3(1):38-45.

[3] 周晓,李杰,边裕挺.基于无线传感网络的环境温度监测系统设计[J].浙江工业大学学报，2013，41(4):440-443.

[4] SHNAYDER V, HEMPSTEAD M, CHEN B, et al. Simulating the power consumption of large-scale sensor network applications[C]// Proceedings of the Second ACM Conference on Embedded Networked Systems (SenSys). Baltimore, MA, USA: Association for Computing Machinery,2004:188-200.

[5] XIAO Jin-jun, CUI Shu-guang, LUO Zhi-quan, et al. Power scheduling of universal decentralized estimation in sensor networks[J]. IEEE Transactions on Signal Processing,2006,54(2):413-422.

[6] RIBEIRO A, GIANNAKIS G B, ROUMELIOTIS S I. SOI-KF: Distributed Kalman filtering with low-cost communications using the sign of innovations[J]. IEEE Transactions on Signal Processing,2006,54(12):4782-4795.

[7] SCHIZAS I D, GIANNAKIS G B, LUO Zhi-quan. Distributed estimation using reduced-dimensionality sensor observations[J]. IEEE Transactions on Signal Processing,2007,55(8):4284-4299.

[8] ZHU Hao, SCHIZAS I D, GIANNAKIS G B. Power-efficient dimensionality reduction for distributed channel aware Kalman tracking using WSNs[J]. IEEE Transactions on Signal Processing,2009,57(8):3193-3207.

[9] BITTANTI S， CUZZOLA F A. An LMI approach to periodic discrete-time unbiased filtering[J]. Systems and Control Letters,2001,42(1):21-35.

[10] ZHANG Wen-an, YU Li, FENG Gang. Optimal linear estimation for networked systems with communication constraints[J]. Automatica,2011,179(22):3944-3955.

[11] 俞立．鲁棒控制-线性矩阵不等式处理方法[M]．北京：清华大学出版社，2003．

[12] KLATT K U, ENGELL S. Gain-scheduling trajectory control of a continuous stirred tank reactor[J]. Computers and Chemical Engineering,1998,22(4/5):491-502.