二维排样中小生境粒子群算法的研究与应用
,
(浙江工业大学 信息工程学院,浙江 杭州 310023)
排样是指将多片不规则形状的零件在某个规定大小的区域中按最佳的方式进行排放的过程,并要求各个零件互不重叠.排样在造船、布匹和皮革加工业中有着广泛应用.排样效率的微小提升可带来巨大的经济效益[1].
粒子群算法(PSO,全名Particle swarm optimization)是一个在连续的定义域内搜索函数极值的有效方法[2].PSO算法具有操作简单、收敛速度快的特点,但也容易陷入局部极值,搜索结果不够理想.因此许多学者提出改进型的PSO算法[3-4].小生境技术起源于遗传算法,这种方法能使基于群体的随机优化算法形成物种,从而使相应的优化算法具有发现多个最优解的能力[5].针对排样问题,提出了一种基于小生境的粒子群算法,利用其保持物种进化过程中的多样性的特点弥补了粒子群算法容易陷入局部最优的缺陷,一定程度上改善了搜索效果,在实际排样中提高了材料利用率.
1 零件轮廓预处理与排样过程
1.1 零件轮廓预处理
由于二维不规则零件的轮廓的复杂性,可以通过将零件的不规则轮廓转化为一系列坐标区间从而脱离不规则几何轮廓的复杂性进行排样预处理[6].不规则零件的离散化几何表达即图形的扫描转换方法,其思想是:用等间距的水平扫描线与不规则多边形相交,从而得到由交点坐标组成的多边形几何轮廓上的水平线段区间,因此可以把不规则多边形看作是由一系列的水平线段区间构成[7],如图1所示.此处确定水平线间距为1 mm,即精度为1 mm.

图1 几何离散化
预处理基本步骤如下:
1) 将轮廓各点按顺序依次排列,形成封闭区间(如图1中顺序:a-b,b-c,c-d,d-e,e-f,f-g,g-h,h-i,i-a).
2) 对各区间线段离散化,记录离散化后各点的二维坐标(x,y),轮廓线段交点记两次.
3) 遍历轮廓最低点至最高点的所有水平线,从最左端沿水平线向右查找,第2n-1个点为区间线段起点,第2n个点为区间线段终点(n=1,2,3,…),如图1中区间m-n,o-p,q-r.
1.2 基本排样过程
采用文献[8]提出的BL(Bottom left)算法进行零件的底层排样.
BL算法的基本思想:零件先从材料的左下角排入,后面的零件往右依次排入,当零件超出材料的右侧时,将零件相对于材料上移,并从左边开始重新搜索材料的剩余空间,如此循环往复,直至样片全部排入或样片溢出材料顶部时停止,即排样高度记为H.
2 基于小生境的粒子群算法
在粒子群算法中,所有材料样片的某个状态的集合被视为一个个体(粒子),状态包括三种:排入次序(order,1—n,n为样片总数)、旋转角度(angle,0°~360°)、镜像(mirror,关于y轴对称,0~1).那么某片材料的位置、速度信息可分别表示为x=
2.1 经典PSO算法
假定种群粒子个数为R,材料样片数位N,那么粒子数第i个粒子的位置可记为Xi=
(1)
式中:d为迭代次数;c1,c2分别为学习因子;rand1,rand2分别为0~1之间的随机数;惯性权值w(d)随迭代次数线性递减:w(d)=wmax-wmin·d/D,其中wmax,wmin分别为最大和最小设定值,D为最大迭代次数.
2.2 基于小生境的粒子群算法
2.2.1 小生境思想的引入
在经典PSO的基础上引入小生境的思想,假定初始种群粒子个数R=P·Q,P和Q均为正整数,将初始种群均分为P个子群(即小生境),通过计算每个粒子的欧式几何距离,将粒子按欧式几何距离从小到大的顺序排列,依次取出粒子,每Q个组成一个子群.
因此,相比于经典PSO算法,新算法需增加变量:子群的历史最佳位置,记为GSp=
若在式(1)中将Gbest项完全由Bsj替代,那么属于不同子群的粒子趋向性会有所不同,从而避免整个种群趋向于同一目标以致种群过早收敛、陷入局部极值的问题;但同时种群的收敛速度将变慢,时间效率大大降低.考虑上述问题,本方法提出的新算法将式(1)改造为
(2)
(3)
式中:p为子群序号;q为子群中某粒子的序号.因此,p·Q+q等效于式(1)中的i,下标pqn等效于式(1)中的in.根据式(3)易得:当d>2D/3或d为偶数时,式(2)等同于式(1);否则式(1)中的种群历史最佳位置项gi(d)变为子群历史最佳位置gspn(d).
由上所述可知:新的算法在前2D/3的迭代次数内时,趋向种群历史最佳位置与趋向子群历史最佳位置的操作交叉进行,这使得粒子能够在更大范围内,搜索更优解,且此操作可在一定程度上防止粒子的进化停滞(粒子信息保持不变).同时,由于种群最优解的作用,算法的收敛作用也不至于被减弱许多.在迭代的后期(后D/3),我们认为,算法已接近全局极值点,因此进行全速搜索,即不再考虑子群最优解的影响,在种群最优解的周围进行细致搜索,以期得到更优解.
2.2.2 加入小生境的重置机制
针对PSO算法容易陷入局部最优解的问题,新算法中加入了子群的淘汰与重置机制,当某个子群在连续n次迭代过程中都未找到更优解时,那么,认为该子群陷入了局部极值解,此时通过对子群的随机重置,可使该子群有机会跳出局部极值解,从而进一步增强了算法的全局搜索能力.
2.2.3 算法流程
基于小生境的粒子群算法(NPSO)流程如下:
1) 随机初始化整个粒子群的初始位置与速度.
2) 根据粒子的欧式几何距离将种群分成多个子群.
3) 使用公式(2)更新每个粒子的速度与位置.
4) 根据粒子位置使用BL算法进行排样,计算适应度值F=1/排样高度.
5) 根据F的值更新粒子,子群以及整个种群的当前最优解.
6) 判断子群在连续n代内的最优解是否有更新,若有,则跳到步骤8);否则执行步骤7).
7) 重置该子群的位置与速度.
8) 迭代次数n=n+1,判断n是否为最大迭代次数,如是,则跳出迭代过程,执行结束;否则转到步骤3)继续执行.
3 仿真实验与结果分析
仿真环境:硬件配置为Core 2双核,主频2.93 GHz,内存为1.96 GB;软件配置为Windows XP系统,VC 2008软件开发平台.
本方法以22块不规则服装样片作为测试对象,采用宽1 200 mm,长度没有限制的长方形作为排样底板.为了测试算法的性能,使用新提出的NPSO算法与标准PSO算法[9]分别进行排样,取相同的实验参数,两种算法的最大迭代次数为500次,惯性因子w(d)=0.9-0.5d/500,种群的粒子个数为30,NPSO算法分5个子群,每个子群拥有6个粒子.本实验中样片的旋转角度以90°为基本单位.两种算法的排样过程各重复30次,实验结果如表1所示.
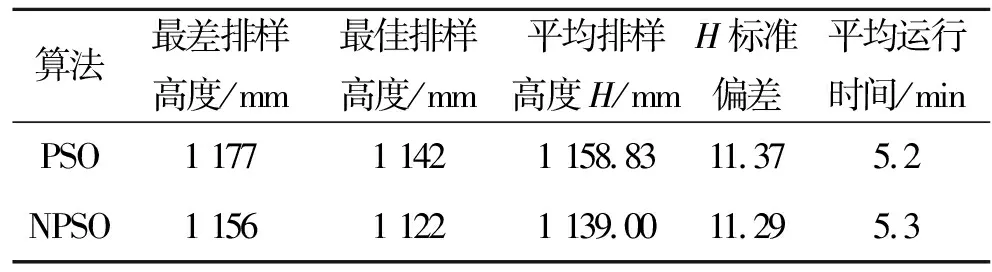
表1 实验数据对照表
从表1可知:两种算法在运行时间和标准偏差上几乎相同;但从排样高度来看,NPSO要大大好于PSO.
图2给出了两种算法的最佳排样方案的效果图.对比图2(a,b)可看出:使用新提出的NPSO算法比PSO算法排列的更紧凑,效果更优.
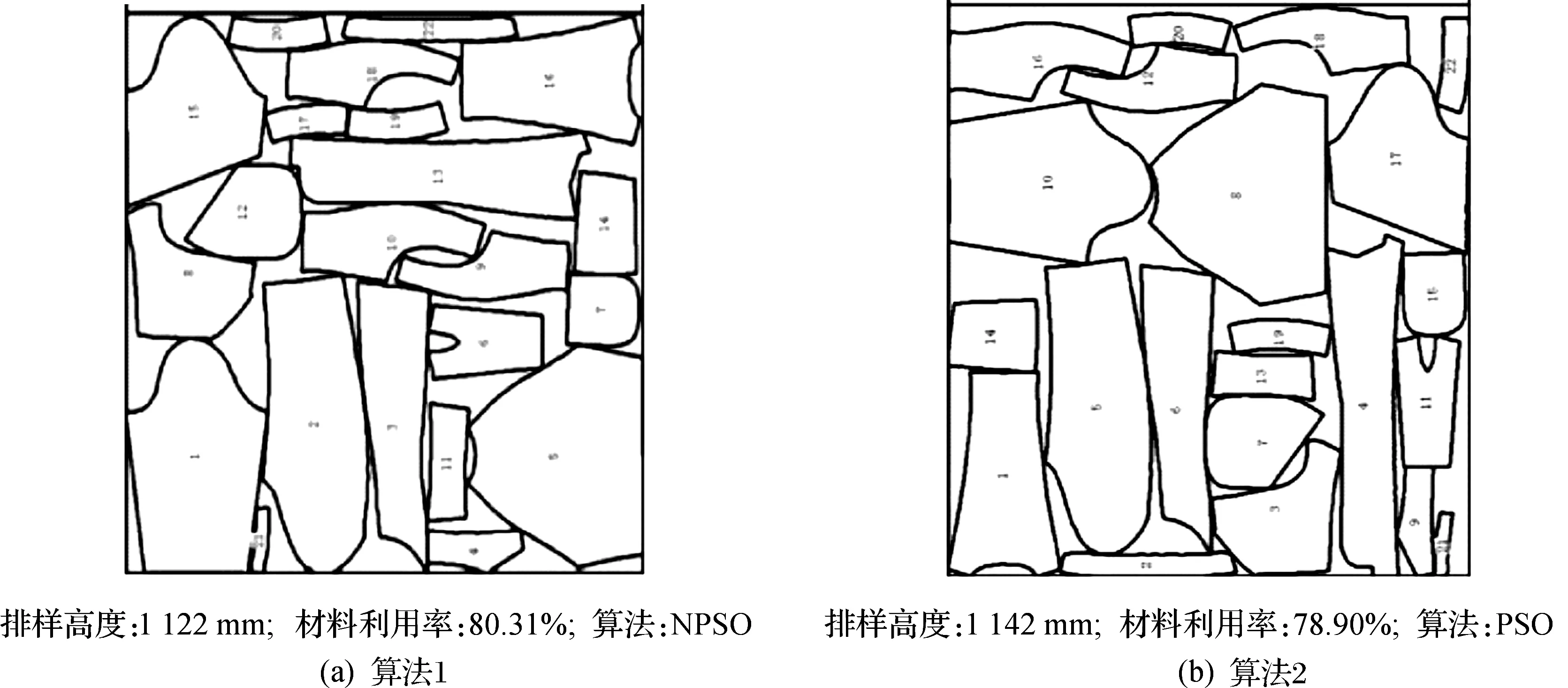
图2 两种算法最佳排样效果图
4 结束语
粒子群算法思路简单,易于实现,通过对两种粒子群算法步骤的介绍和仿真实例的数据结果分析,新提出的基于小生境的粒子群算法的性能明显好于未经过改良的粒子群算法,前者在未改变时间复杂度的前提下,其全局搜索能力比后者有较大提升,弥补了粒子群算法的最大不足.通过上述仿真可知:将基于小生境的粒子群算法应用到解决二维不规则排样的问题中是可行的,而且它在实际应用中,可以有效提高材料利用率.
参考文献:
[1] 刘虓,叶家玮,胡金鹏.基于最小使能原理的不规则零件排样算法[J].华南理工大学学报,2011,39(8):26-41.
[2] 韩毅,蔡建湖,周根贵,等.线型结构批量计划问题的粒子群算法参数方案设定[J].浙江工业大学学报,2010,38(6):683-692.
[3] 盛煜翔,潘海天,夏陆岳,等.混合混沌粒子群算法在苯与甲苯闪蒸过程优化中的应用[J].浙江工业大学学报,2010,38(3):318-321.
[4] 韩冬梅,王丽萍,吴秋花.基于模糊偏好的多目标粒子群算法在库存控制中的应用[J].浙江工业大学学报,2012,40(3):348-351.
[5] 章军.小生境粒子群优化算法及其在分类器集成中的应用研究[D].合肥:中国科学技术大学,2007.
[6] 陈勇,唐敏,童若锋,等.基于遗传模拟退火算法的不规则多边形排样[J].计算机辅助设计与图形学学报,2003,15(5):598-609.
[7] 黄建江.智能数控裁床的研究与开发——二维不规则零件排样算法的设计与应用[D].无锡:江南大学,2007.
[8] STEFAN J. On genetic algorithms for the packing of polygons[J].European Journal of Operational Research,1996,88:165-181.
[9] SHI Yu-hui, EBERHART R C.A modified particle swarm optimizer[C]//Proc IEEE World Congress on Computational Intelligence. New York: IEEE Press,1998:69-73.

