基于BP译码算法的准循环低密度奇偶校验码量化问题研究
,,
(浙江工业大学 信息工程学院,浙江 杭州 310023)
低密度奇偶校验码是一种校验矩阵稀疏的线性分组码,由Gallarger在60年代提出[1-2].1995年前后,LDPC码又被人们所重新重视,有MacKay和Neal[3]提出的可行性迭代译码算法——置信算法(BP algorithm)[4],对LDPC码的发展具有很大的推动作用.LDPC码具有并行的译码结构,更适于高速硬件实现,每比特译码所需的计算量更少,错误平层更低[5],但由于BP译码算法在硬件实现太过复杂,所以经过改进,得到了对数似然比译码算法(LLR BP).这种改进的BP译码算法可以大大降低硬件实现的复杂度,同时减小性能的损失.与此同时数据量化的合理性对译码算法硬件的实现以及准确性方面也有很大的影响.笔者着重研究低密度奇偶校验码LLR BP译码算法的量化问题,对量化范围、量化比特数、量化方式[6-7]这三方面进行了讨论和比较,最终得到一个比较合理的量化方案,从而保持了较低的译码误码率,减少译码算法的错误平层,达到更高的译码性能.
1 LDPC码简介
低密度奇偶校验码是一种线性码,通常可以用校验矩阵对其进行表示,并且其校验矩阵H中‘1’的密度很低[8].LDPC码可以分为规则和非规则两种.规则的LDPC码可以用(N,j,k)来表示,其中:N为码长;k为校验矩阵每行中1的个数;j为校验矩阵每列中1的个数,规则的LDPC码每行具有相同的行重和每列具有相同的列重.且每两行(列)最多只有一个相同的位置上的1.j,k相对于行数与列数来说都非常小,且j小于k.相对于规则码,非规则LDPC码指的是其每行(列)的行(列)重并不相同.我们可以用度数分布(λ,ρ)来表示.这里先介绍二分图的概念,非规则LDPC码的二分(Tanner)图如图1所示.

图1 一种非规则LDPC码的Tanner图
上排校验节点代表校验矩阵中的每一行,即校验方程,下排的变量节点代表每一列.其中变量节点(Variable nodes)用圆点表示,校验节点(Check nodes)用方框表示[9].每个校验节点和变量节点之间的连线表示这一行这一列位置上的元素值为1.每一个校验节点都会向相连接的变量节点传输消息的同时进行求和计算,同样的每个变量节点也进行相同的步骤.对于非规则LDPC码来说,我们可以通过其度分布进行多项式的构造,即
(1)
(2)
式中:dv为变量节点中最大度数;λi为变量节点中i的度数占总度数的比率;dc为校验节点中最大度数;ρi为变量节点中i的度数占总度数的比率[10].
2 LLR BP译码算法原理
这部分简单介绍一下LLR BP译码算法原理[11].首先定义初始消息.假设信道中初始化消息似然比为
(3)
校验节点传输的似然比消息为
(4)
变量节点传输的似然比消息为
(5)
判决译码时变量节点接收的全信息[12]为
(6)
1) 初始化.传递消息之前,要首先计算信道传输给所有变量节点的初始似然比消息L(Pi),这里i=1,2,…,n.对每一个变量节点i和与其相邻的校验节点j∈C(i),设定变量节点i传递给校验节点j∈C(i)的初始消息为:L(0)(qij)=L(Pi).
2) 迭代处理过程.水平方向步骤:由校验节点向变量节点传输消息.对所有校验节点j和与其相邻的变量节点i∈R(j),第l次迭代时,计算第j个校验节点传递给第i∈R(j)个变量节点的消息,即
(7)
垂直方向步骤:由变量节点向校验节点传输消息.对所有变量节点i和与其相邻的校验节点j∈C(i),第l次迭代时,计算第i个变量节点传递给第j∈C(i)个校验节点的消息[13-15],即
(8)
硬判决步骤:后验似然比率的计算,即
(9)
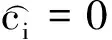
3 LLR BP译码算法的量化性能分析与仿真
因为数据的量化对硬件的实现与性能有很大影响,所以这里我们将对LLR BP译码算法中的输入信号以及两个中间变量L(rij)和L(qij)分别进行量化处理.量化是对抽样后的信号取值,将抽样值的范围分为M个区间,每个区间用一个电平表示,这种方法称为量化[16].量化又分为均匀量化和非均匀量化.M个抽样值区间是等间隔划分的就是均匀量化,M个抽样值区间不是等间隔划分的就是非均匀量化.信号在进行量化的过程中会引入量化噪声,我们要尽量减小这个量化噪声,提高信号量噪比.通过量化方式,量化范围以及量化比特的对比和选择,可以尽量得到一个比较好的量化方案,从而减小量化误差.
3.1 输入信号的量化
由于QC-LDPC码的生成矩阵和校验矩阵都是准循环矩阵,因此相比于随机构造的LDPC码来说,具有较低的编译码复杂度[13],所以采用基于802.16e标准,并经过编码的准循环奇偶校验码(QC-LDPC),其码率为1/2,码长1 056[17-18].图2为该码H矩阵的示意图,矩阵维度528×1 056,横坐标为矩阵中的行,纵坐标为矩阵中的列.从图2中看出:码的结构近似于上三角结构,有利于减小译码复杂度.
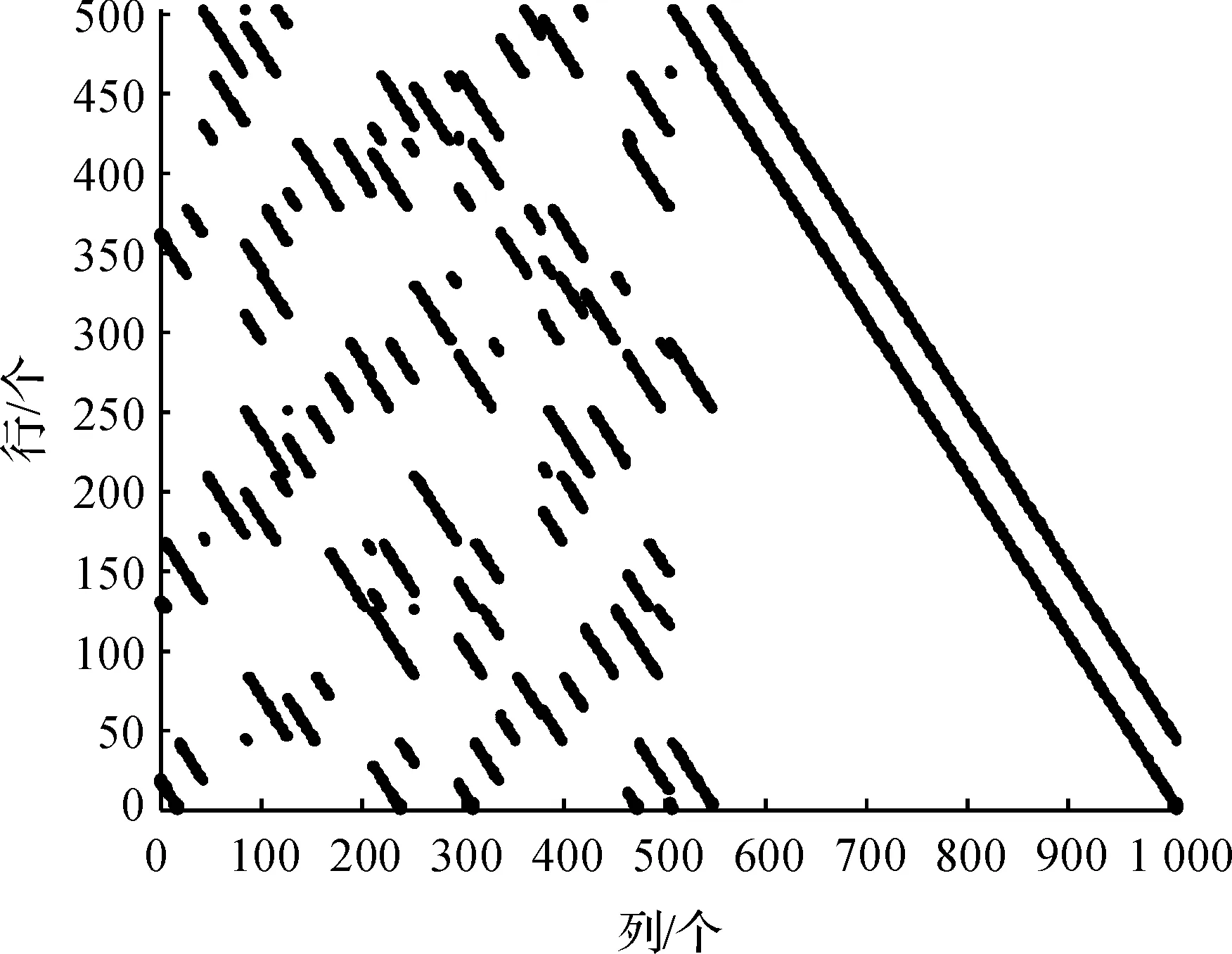
图2 基于802.16e标准的循环奇偶校验码
这里对发射信号采用的是BPSK调制[19].设信号为{ci|i=1,2,…,n,ci∈{0,1}},经过调制,0→+1,1→-1产生已调信号{xi|i=1,2,…,n,xi∈{-1,1}},信号源为等概发送.假设接收信号为yi=xi+ni,这里xi为已调信号,是一个离散型随机变量,故而xi的特征函数为
(10)
ni为噪声,服从高斯分布N(0,σ2),故其特征函数为
(11)
又因为xi和ni相互独立,根据特征函数的性质,两个相互独立的随机变量之和的特征函数等于它们的特征函数之积,故yi的特征函数为
(12)
经过傅里叶变换,yi对应的概率密度函数f(x)和累积分布函数F(x)为
(13)
(14)

图3 接收信号概率密度曲线
图3是码率为1/2,信噪比从1~3 dB,间隔1 dB的接收信号的概率密度图.图4为该接收信号的累积分布图.从图4可以看出:在σ=1时,接近于99%的接收信号基本都落在了范围[-4,4]上.因此我们可以将量化范围取为[-4,4].

图4 接收信号累积分布曲线
非线性量化随信号的变化取不同的量化间隔,实现起来比较复杂,考虑到运算复杂度和硬件消耗,文中均采用均匀量化方式.对输入信号分别进行6,8,10,12比特数的量化,量化范围均取为[-4,4].如图5所示,与未量化相比,6比特均匀量化已经能够达到很好的译码性能,随着量化比特数的增加,其效果几乎无区别.

图5 输入信号不同比特数量化
3.2 中间变量L(rij)和L(qij)量化处理
在译码过程中,还会涉及到中间变量的问题.对于中间变量来说,其数目比较多,且容易发生数据溢出,我们要保证译码过程中不出现因溢出导致的译码性能恶化.在LLR-BP译码算法中,有两个中间变量L(rij)和L(qij).
图6为两个中间变量的概率密度图,分别给出了一次迭代,五次迭代和最后一次迭代结束后统计的所有变量的概率密度曲线.其信噪比从1~3 dB,间隔为1 dB.从图6中可以看出:随着迭代次数的增加,中间变量的范围逐渐增大,在最后一次迭代结束后,中间变量L(rij)大部分落在区间[-7.5,7.5]中,L(qij)信号大部分都落于区间[-20,20]中.故而我们将L(rij)量化范围取为[-7.5,7.5],L(qij)量化范围取为[-20,20].
对于中间变量,我们同样采用均匀量化.这里,对译码算法的中间变量做量化处理的同时,也对其对应的输入信号做相同比特的处理.分别对输入信号和中间变量做未量化,6比特均匀量化,8比特均匀量化,10比特均匀量化和12比特均匀量化处理.输入信号的量化范围均取为[-4,4],中间变量L(rij)的量化范围取为[-7.5,7.5],L(qij)的量化范围取为[-20,20].从图7中可以看出:随着量化比特数的增加,性能也越来越好,10比特均匀量化已经达到一个不错的译码性能,而12 bit均匀量化比之更优.考虑到运算复杂度和硬件资源的消耗,最终选取10比特均匀量化作为中间变量的最终量化方案.


图6 中间变量的概率密度曲线

图7 中间变量不同比特量化仿真
4 结 论
基于LDPC码的LLR BP译码算法,对其输入信号,中间变量等参数进行了量化分析.着重讨论了在高斯白噪声信道下,量化方式,量化范围以及量化比特数对LDPC码的影响.仿真结果表明:对于输入信号,在范围均取为[-4,4]的条件下,采用6比特均匀量化时已经可以达到一个很好的性能,随着比特数的增加没有明显区别.在对输入变量和中间变量均采用相同比特均匀量化时,选择量化比特为10,变量L(rij)量化范围取为[-7.5,7.5],L(qij)量化范围取为[-20,20],可以在尽量减少运算复杂度的同时也得到一个比较良好的译码性能.采用上述方案,可以比较有效的消除错误平层,更大程度的获取译码性能,同时也对LDPC译码的硬件实现有着重大意义.
参考文献:
[1] GALLAGER R G. Low-density parity-check codes[J]. IRE Transactions on Information Theory,1962,8(1):21-28.
[2] GALLAGER R G. Low-density parity-check codes[D]. Cambridge:Cambridge University,1963.
[3] MACKAY D, NEAL R. Near Shannon limit performance of low density parity check codes[J]. Electronic Letters,1996,32(18):1645-1646.
[4] KSCHISCHANG F R, Frey B J. Iterative decoding of compound codes by probability propagation in graphical models[J]. Selected Areas in Communications, IEEE Journal on,1998,16(2):219-230.
[5] 窦金芳,王楠,周宇昌,等.LDPC码在深空通信中的应用[J].遥测遥控,2009,30(1):30-35.
[6] PING L, LEUNG W K. Decoding low density parity check codes with finite quantization bits[J]. Communications Letters, IEEE,2000,4(2):62-64.
[7] HE Yu-cheng, SUN Shao-hui, WANG Xin-mei. Fast decoding of LDPC codes using quantization[J]. IEEE Electronics Letters,2002,38(4):189-190.
[8] 李秋玲.基于动态消息调度的LDPC码及数字喷泉码改进译码算法研究[D].成都:西南交通大学,2012.
[9] 辛勇.基于快速拥阻密度估计的布局优化[D].上海:上海交通大学,2006.
[10] 高冰.串行级联生成阵码编译码算法研究[D].北京:北京邮电大学,2011.
[11] 魏瑞刚,陈晖,邱金蕙,等.高速数据传输中的LDPC码译码算法研究[J].无线电工程,2011,41(3):20-22.
[12] 王博.低信噪比卫星通信中的编码与解调技术研究[D].杭州:杭州电子科技大学,2012.
[13] 徐艺萍.多标准DTV中LDPC译码算法的研究与设计[D].武汉:武汉理工大学,2012.
[14] 刘帆洨.LDGM码及其在协作编码中的应用研究[D].成都:西南交通大学,2010.
[15] 王巽冬.卷积LDPC码编译码研究[D].哈尔滨:哈尔滨工业大学,2011.
[16] 刘艺美,吴康.基于2PSK无线载波通信系统的研究[J].信息通信,2013(7):27-28.
[17] 胡潘,李珊珊,赵宏宇.基于WIMAX的LDPC码性能研究[J].通信技术,2011,44(4):28-30.
[18] 杨建平,陈庆春.IEEE802.16e标准LDPC译码器设计与实现[J].通信技术,2010,43(5):84-86.
[19] 应亚萍,许建凤,陈婉君.2FSK调制解调系统的FPGA设计与实现[J].浙江工业大学学报,2010,38(3):282-285.

