两种类型的不定积分问题

毛北行,孟晓玲

(郑州航空工业管理学院 数理系，河南 郑州 450015)

0 引言

数学的各部分之间互相渗透，且有内在联系是数学的主要特征之一[1-4]，而这种联系往往隐蔽于某些表面似乎毫不相关的问题中，本文讨论了两种类型的不定积分问题，即一类可用分部积分公式求出递推公式的积分，文中第二种类型的积分讨论了可转化为方程组进行求解的不定积分问题.，对于这类不定积分[5]，可以通过构造方程组来求解，而且能够降低求解的难度.

1 类型1：下述函数求不定积分

采用分部积分法

第二项积分，作代换x=tant

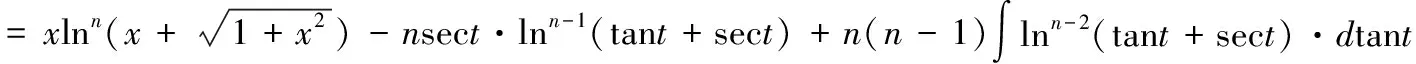
考虑到x=tant，所以得到：

上式对于n≥3都成立

以下来分别计算n=1,2两种情况

采用分部积分法

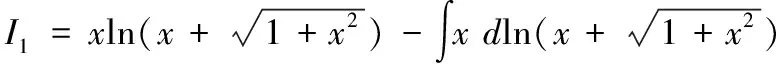
若规定I0=I-1=0，则I1,I2也满足递推公式In

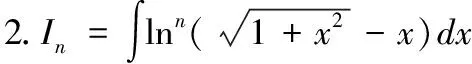
令x=tant

令x=sect

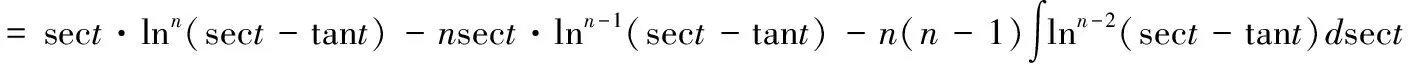
2 类型2：下述函数求不定积分

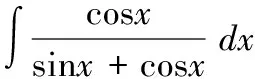
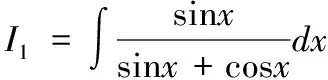
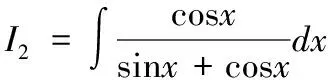
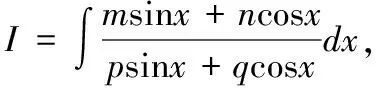
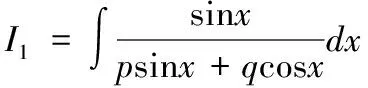
则I=mI1+nI2，因此上述为题转化为求变量I1,I2

=ln|psinx+qcosx|+C2

两个方程两个未知量，解这个线性方程组，很容易求出I1,I2，而I=mI1+nI2就相应的求了出来.

上述题目我们发现有一个共同点：那就是(sinx)′=cosx,?(cosx)′=sinx

因此我把上述问题概括为如下抽象问题：

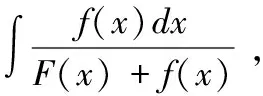
F′(x)=f(x),f′(x)=±F(x)，或者：

F′(x)=±f(x),f′(x)=F(x)

解：上述关系式，即满足：F″(x)=±F(x)

这显然是关于F(x)的二阶线性齐次微分方程

对应的特征方程为：λ2±1=0

(1)若λ2=1则，方程有通解：F(x)=C1ex+C2e-x

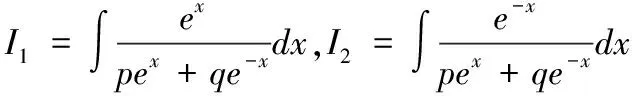
则I=mI1+nI2，因此上述为题转化为求变量I1,I2

解这个线性方程组，很容易求出I1,I2，而I=mI1+nI2就相应的求了出来.

(2)若λ2=-1则，方程有通解：F(x)=C1sinx+C2cosx

3 结束语

从上面这些例题中可见：利用解方程组的方法不仅较简便地求出了原不定积分，而且附带求出了另外一个不定积分；这两个不定积分相辅相成．充分体现了数学的对称美和有机的统一，并展示了一个完整的思维过程和结果.

[1] 高颖.浅谈大学数学教学改革[J].教育时空,2003,12(1):199-200.

[2] 欧阳光中，姚允龙.数学分析[M].上海:复旦大学出版社,2004:197-267.

[3] 同济大学数学系.高等数学(上册)[M].北京:高等教育出版社,2004:114-157.

[4] 数学手册编写组.数学手册[M].北京:高等教育出版社,1979:250—277.

[5] 谢芳.方程组解求不定积分中的应用[J].昭通师专学报,1998,20(4):119-122.

[6] 毛北行,孟晓玲.一类不定积分的一题多解与结论推广[J].科教导刊,2013,10(中旬):42-43.