三维渐进损伤的复合材料层合板低速冲击模型

郭 卫

(上海飞机设计研究院，上海201210)

为了预测复合材料层合板在低速冲击载荷下的损伤扩展情况，虽然很多学者都对其进行过探索性试验，并且提出了很多分析模型来预测层合板的损伤情况.但是因为冲击响应的分析过程比较复杂，因而采用何种损伤和演化准则仍然没有统一的认识.Tan[1]等的渐进损伤分析模型中采用基于壳单元理论进行应力求解，但是却无法较好的反映层合板三维效应和铺层之间的相互作用.Chang[2－3]等在研究T300/976复合材料层合板强度时，根据不同的失效模式将相应的材料弹性常数退化为零，认为层合板一旦发生失效就不可以继续承载，明显与实际不符，因而预测的强度偏小.Camanho[4]等在分析T300/914复合材料层合板接头拉伸强度时，将Tan[1]的参数退化方式扩展到三维，认为材料发生损伤后，其弹性常数退化到一定程度，因此退化系数需要大量的试验进行测定，另外由于层合板的弹性系数突然降低同时会造成刚度矩阵的奇异，很容易发生计算无法进行.为了解决这些问题，张彦[5－6]等使用 ABAQUS 建立了以基于应变Hashin失效准则基础上的层内损伤，并通过结合传统的应力失效准则定义了损伤演化规律，但是由于文中提出的损伤演化规律没有考虑到能量释放率和损伤力学对于网格的依赖影响，因而对于预测的分层面积和实验值相差很大.

本文基于有限元软件ABAQUS对复合材料层合板低速冲击，建立了一个有效反映复合材料层合板面内和层间的非线性损伤模型，该模型基于三维实体单元和内聚力单元可以有效分析层合板层内和层间失效行为.对于复合材料层合板面内损伤，以改进的Hashin失效准则作为起始损伤准则，提出了一种基于能量释放率的损伤变量指数渐进演化模型，既描述了复合材料损伤的渐进失效过程，又避免了材料刚度突然下降导致刚度矩阵奇异的不足，同时引入特征长度来降低网格的依赖性，最终建立了单层板的渐进损伤非线性分析模型.该损伤模型通过商用有限元软件ABAQUS/Explicit的用户子程序VUMAT实现，并使用该模型对复合材料层合板在横向低速冲击作用下的损伤和变形行为进行预测分析，数值仿真的结果与试验结果进行了比较，吻合良好，验证了该模型的有效性.

1 复合材料三维渐进损伤模型

1.1 层合板面内渐进损伤模型

本文中考虑的失效模式包括纤维断裂、纤维挤压、基体开裂和基体挤裂4种模式，每种失效模式可以看作是在结构损伤过程中当一种特定的应力分量组合达到特定值时的一种明显状态，因此本文采用被众多研究人员普遍认可的三维Hashin失效准则[7]，其具体形式:

1)纤维断裂

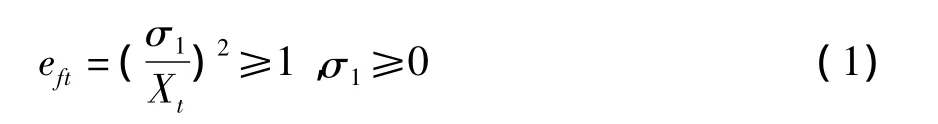
2)纤维挤压

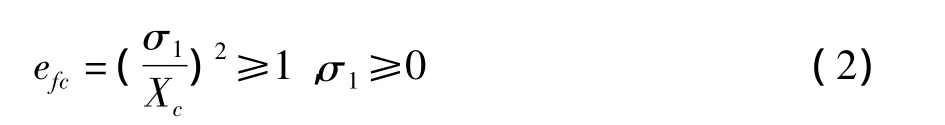
3)基体开裂

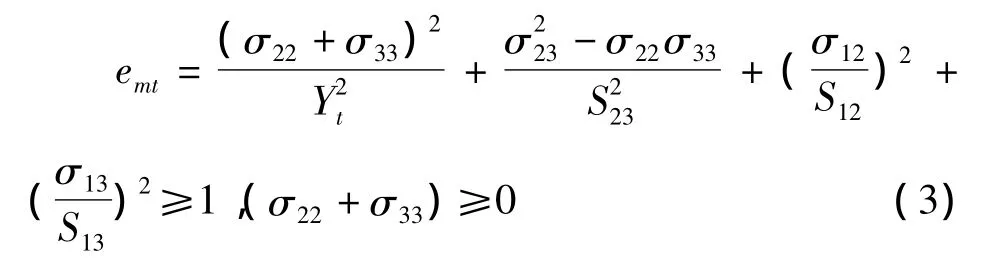
4)基体挤裂

199年，国际集群协会以波特的钻石模型为基础，探讨了南非旅游产业集群集聚机制和范式。他们认为旅游产业集群是指旅游企业为了达到共同的目标，实现区域竞争优势最大化，而和相关组织机构在地理上形成集中[3]。2003年，ETRI研究人员Sare Nordin运用波特钻石模型分析旅游企业集群化发展的前提条件[4]。Radovan等人根据对多瑙河地区旅游集团成员态度的调查，分析了其对提高乡村旅游目的地竞争力的贡献，以波特竞争力模型确定多瑙河地区乡村的优势和劣势，并将其作为潜在的旅游目的地[5]。

其中:σi为单元的正应力，σij为单元的剪应力，Xt、Xc、Yt、Yc、S12、S23、S13分别为轴向拉伸、轴向压缩、横向拉伸、横向压缩和各方向剪切强度.只要单元内的各应力分量满足上述一个式子，即认为发生了该式子对应的破坏的模式.

当复合材料积分点满足失效准则时，其材料积分点应力和刚度开始发生退化，进行应力更新.本文引入连续损伤变量来预测复合材料结构内部损伤的产生和演化，特征值dft表示纤维断裂，dfc表示纤维挤压，dmt表示基体开裂，dmc表示基体挤裂，这些损伤变量的定义域为[0，1]，当d=0时，表示没有损伤产生，当d=1时，表示材料完全破坏失效了.

使用上面四个损伤变量定义全局损伤，对于纤维损伤使用df来表征，对于基体损伤使用dm来表征:

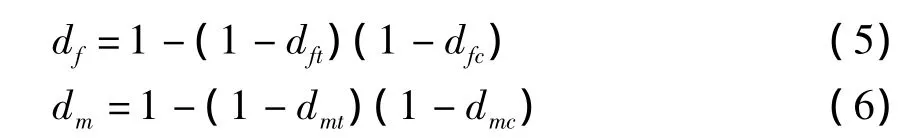
当材料积分点满足失效准则时，其刚度矩阵可以根据下面方程计算:

当复合材料发生损伤，对于纤维增强复合材料损伤累积引起的材料非线性，本文提出使用非线性指数函数定义损伤演化规律的方法，使材料性能逐渐下降，该方法可以避免刚度矩阵退化过程中矩阵的奇异性，又可以通过控制能量释放率保证材料刚度的迅速折减，达到积分点损伤破坏的目的，最终保证计算的顺利有效进行.

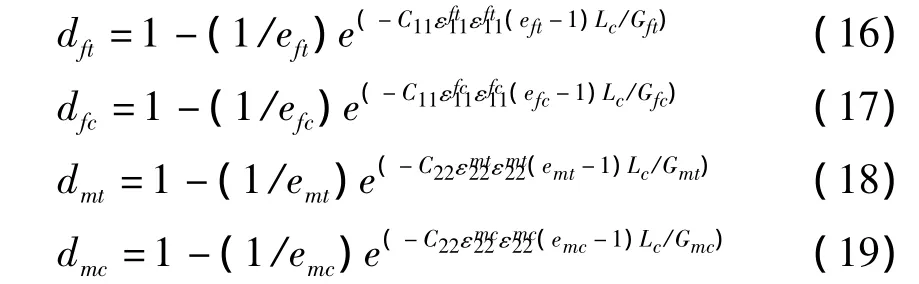
其中:Gft、Gfc、Gmt和 Gmc材料临界断裂能，Lc是单元的特征长度，本文参考ABAQUS，在损伤材料点的应变软化区域引入单元特征长度来降低其对于网格的敏感性，减小其对于网格的依赖特性.

1.2 层合板层间渐进损伤模型

大量试验表明，层合板的分层损伤在铺设角度不同的两相邻子层之间的界面处产生并扩展，因此把内聚力单元引入到可能发生分层的位置可以有效的预测分层损伤的产生、损伤扩展直至最后分层的发生.定义内聚力单元的应力分量为 t1、t2、t3，ε为求的内聚力单元名义应变，可以得到本文所使用的内聚力单元本构关系如下:其中:kn、ks、kt分别是内聚力单元法向刚度和切向刚度.

Alfano[8]对双线性本构、梯形本构、指数本构、和线性抛物线内聚力模型做了分析比较，综合看在静态载荷作用下的中，双线性准则无论对于计算的经济行还是准确性以及收敛特征都是很好的选择，因此本文选择双线性本构模型来进行复合材料层合板的层间渐进损伤分析，其双线性本构模型典型的相对位移－牵引力曲线如图1.

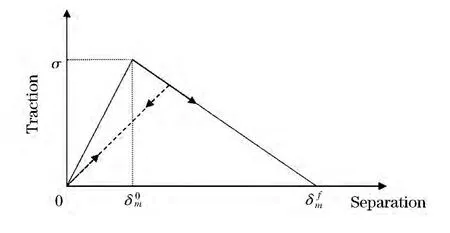
图1 双线性本构模型典型曲线

根据图1，可以给出初始破坏点对应的界面相对位移，如下:

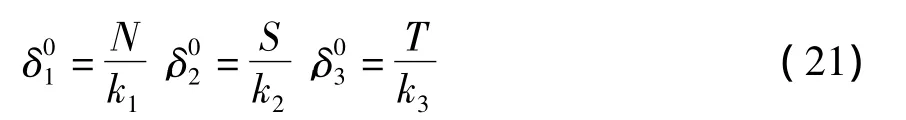
其中:N为界面的法向强度，S、T为界面的剪切强度.

混合模式下的内聚力单元损伤扩展判据采用由Benzeggaph和 Kenane[9]提出的 B －K 准则，该准则考虑了不同裂纹模式下应变能释放率直接的耦合关系，其表达式如下:

其中:GT=GI+GShear

2 复合材料层合板低速冲击分析算例验证

2.1 模型参数

试验中层合板尺寸150×100 mm，厚度5.8 mm，铺层方向[454/04/－454/904]s对称铺层其基本力学性能见表1，层间性能见表2，通过四个刚性压头固支形成一个125×75 mm的冲击区域.刚性冲头为半球形，前端直径为 16 mm，质量为 5 kg[10].

表1 单层板材料基本力学性能

表2 层间强度及层间韧性

2.2 有限元模型建立

为了降低边界约束对试验结果的影响，本文在对复合材料层合板低速冲击部分建立有限元模型时，建立了试验中所有部件，即刚性底座、四个刚性压头、试验层合板、以及刚性冲头四部分，层合板子层选择沙漏增强的C3D8R单元;层间选择内聚力(CHO3D8)单元，其余全部选择离散刚体.为了保证接触区域分析精度，划分网格中部60×60区域内进行细化，其余部分按比例划分;四个刚性压头施加预紧位移0.015 mm，低速冲击的有限元模型如图2所示.

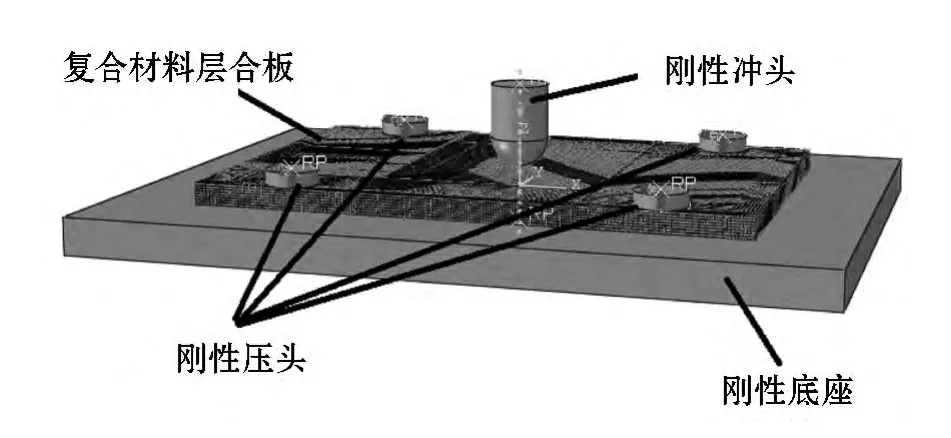
图2 复合材料层合板低速冲击有限元模型

2.3 数值仿真结果及讨论

本文主要对冲击能量为19.3 J试验进行分析，图3中显示了数值计算和试验中冲击接触力随时间的变化曲线，从图3中可以看出冲击接触力峰值和试验值吻合的很好[11].

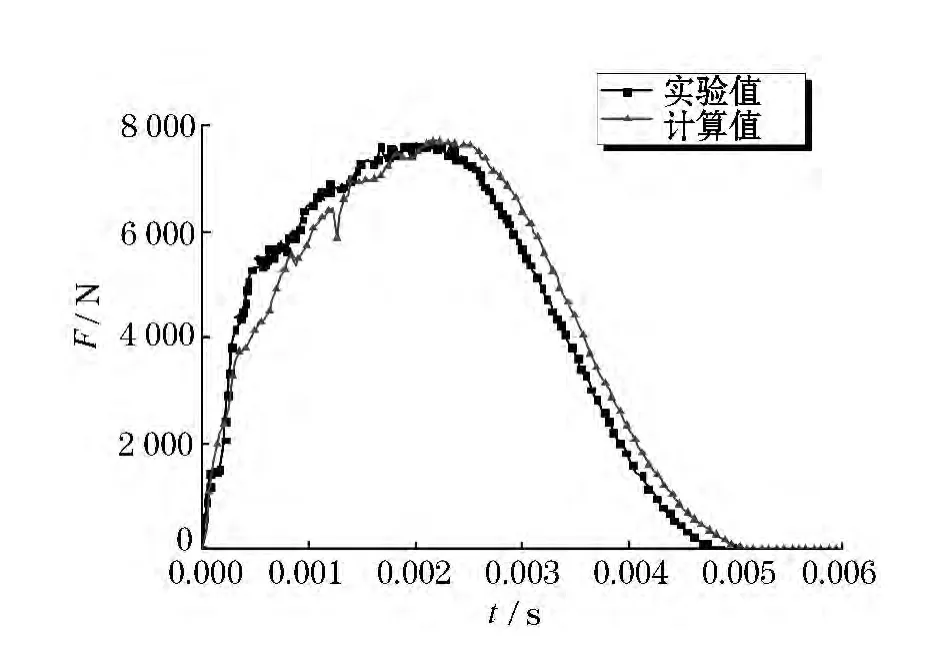
图3 冲击能量为19.3 J下的接触力时间曲线

图4为其各子层的基体损伤形状以及各层间分层，由图4可知，各层间的分层形状基本呈现对称的双叶形，即花生状，主轴方向沿着下层纤维的铺设方向，且靠近冲击背部的界面分层面积要大于靠近冲击点处的界面分层面积;基体损伤通常沿着该层纤维方向的带状分布，越是靠近冲击背部，基体开裂的长度越大，但发现靠近底层的铺层基体的方向沿着方向，其原因是因为其处在和之间，铺层角度变化最大，并且其下方有大面积分层出现，改变了该层的应力分布所致.

图5所示冲击层合板后使用C扫描得到的分层面积，图6所示是使用绘图软件描边得到的数值计算和试验对比结果，从图5中可以看出分层面积在其沿长度和宽度的两方向上最大尺寸吻合的很好，但是整个投影面积有一定的误差，其试验投影面积最大值为4 000 mm2，图6是其数值计算的所有分层的投影面积，其值为4 450.9 mm2，其误差为 11.3%.

图4 各子层的基体损伤形状以及各层间分层形状

图5 试验分层面积

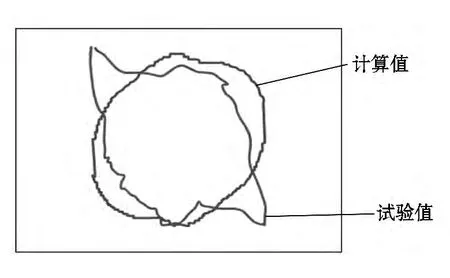
图6 试验与数值计算分层投影面积对比

3 结论

本文基于损伤力学理论，建立了一个反映复合材料层合板面内和层间的三维渐进损伤的非线性损伤模型，研究了复合材料层合板在低速冲击作用下的层内和层间冲击响应下的非线性失效行为，可以得到如下结论:

对于复合材料层合板面内损伤，本文以改进的Hashin失效准则作为起始损伤准则，提出了一种基于能量释放率的损伤变量指数渐进演化模型，既描述了复合材料损伤的渐进失效过程，又避免了材料刚度突然下降导致刚度矩阵奇异的不足，同时引入特征长度来降低网格的依赖性，最终建立了单层板的渐进损伤非线性分析模型.

针对层合板的层间损伤，本文采用内聚力单元来模拟，通过结合传统的应力失效准则和断裂力学中的能量释放率准则定义了界面损伤演化规律.

对试验结果进行对比分析，发现在冲击过程中，层合板最先产生的损伤形式是基体开裂和层间分层，并且是其能量消耗的主要表现形式，冲击造成的基体损伤，其方向一般沿纤维方向，并且越是靠近背部基体损伤较为严重，冲击造成的层间分层主要发生在不同铺层之间，一般呈现双叶形，即花生形，并且主轴沿着下子层的纤维方向，这与试验观察到的现象是一致的.

[1]TAN S C.A progressive failure model for composite laminates containing openings[J].Journal of Composite Materials，1991，25:556－577.

[2]CHANG F C K.A progressive damage model for laminated composites containing stress concentrations[J].Journal of Composite Materials，1987，21:834 －855.

[3]CHANG K，LIU S，CHANG F.Damage tolerance of laminated composites containing an open hole and subjected to tensile loadings[J].Journal of Composite Materials，1991，25:274 －301.

[4]CAMANHO P P，DAVILA C G.Mixed－mode decohesion finite elements for the simulation of delamination in composite material[R].NASA/TM－2002－211737，2002:1－37.

[5]张 彦，朱 平，来新民，等.低速冲击作用下碳纤维复合材料铺层板的损伤分析[J].复合材料学报，2006，23(2):150－157.

[6]张 彦，来新民，朱 平，等.复合材料铺层板低速冲击作用下损伤的有限元分析[J].上海交通大学学报，2006，40(8):1348－1353.

[7]HASHIN Z.Failure criteria for unidirectional fiber composites[J].Journal of Applied Mechanics，1980，47:329 －335.

[8]ALFANO G.On the influence of the shape of the interface law on the application of cohesive － zone models[J].Composites Science and Technology，2006，66(6):723－730。

[9]BENZEGGAGH M L，KENANE M.Measurement of mixed －mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed － mode bending apparatus[J].Composites Science and Technology，1996，56(4):439－449.

[10]DEMOURA M F S F，MARQUES A T.Prediction of low velocity impact damage in carbon – epoxy laminates[J].Composites Part A:Applied Science and Manufacturing，2002，33(3):361－368.

[11]邓以泰，薛 璞，杨 军，等.复合材料工字梁开孔应力补强分析[J].哈尔滨商业大学学报:自然科学版，2013，29(6):711－714.