顾及EGM2008重力场模型的GPS高程拟合研究
程怀远
(中国石油化工股份有限公司西北油田分公司,新疆 轮台 841600)
0 引 言
西北地区地广人稀,交通不便,控制点稀少,获取高程比较困难。GPS可以测量得到高精度的大地高,但我国采用正常高系统,需要进行转换。若有高精度似大地水准面模型, 可以直接获得高精度高程异常进行转换;若测区没有似大地水准面模型,一般通过联测一定数量的GPS/水准点,利用数学拟合法转换;若测区即没有似大地水准面模型,也无足够的GPS/水准点,则通过已有的地球重力场模型直接进行GPS高程转换[1]。常用的GPS水准拟合模型有多项式拟合、多面函数法[2]、BP神经网络法[3]等。单一数学模型的拟合方法忽略了地球重力场的影响,无法符合实际的似大地水准面。顾及地球重力场模型的GPS高程拟合方法值得探讨[4]。
1 方 法
使用Bruns公式计算EGM2008重力场模型高程异常,根据GPS/水准点高程异常计算残余高程异常,采用二次曲面拟合残余高程异常,根据残余高程异常拟合结果及EGM2008重力场模型高程异常将大地高转换为正常高。
1.1 EGM2008地球重力场模型
EGM2008重力场模型是美国国家地理空间情报局采用先进算法和建模技术,以PGM2007B为参考模型,利用GRACE卫星重力数据、全球5′×5′重力异常数据、TOPEX卫星测高数据及现势性好分辨率高的地形数据,结合精度高、分布面广的地面重力数据完成的最新一代全球重力场模型[5],是目前分辨率最高、精度最好、阶次最多的全球重力场模型。
章传银、郭春喜、陈俊勇等根据GPS/水准数据,分别对华北地区、华中华东地区、华南地区、全国的EGM2008重力场模型高程异常进行了对比,对EGM2008重力场模型在中国内地的适用性进行了研究,参与比对的GPS/水准点分布情况见文献[6],精度统计结果如表1所示。

表1 EGM2008重力场模型高程异常与GPS水准高程异常对比
在全国范围内,EGM2008重力场模型的高程异常精度差距较大,西部人烟稀少、环境恶劣、控制点稀少地区精度稍差。
1.2 二次曲面拟合法
二次曲面拟合的数学模型为[7]
ξ(x,y)=a0+a1x+a2y+a3x2+a4y2+a5xy.
(1)
若测区内有n个(n>6)GPS/水准点,则模型的拟合系数可由GPS/水准点的高程异常通过最小二乘原理VTPV=min求定。
设参与拟合点数为n,由式(1)可列误差方程
(2)
表示为总误差方程即
V=BX-L;
(3)
式中:
根据最小二乘原理得式(3)的解为
x=(BTB)-1BTL
由此即可计算得到二次曲面拟合模型参数。
1.3 基于二次曲面的残余高程异常拟合
1.3.1 模型高程异常计算
根据Bruns公式,地球表面上任意一点p的模型高程异常可由公式(4)得到[1]:
Snmsinmλ)Pnm(sinφ),
(4)
式中:φ,λ,ρ为p点的地心纬度、地心经度和地心向径;GM为引力常数与地球质量的乘积;γp为p点的正常重力值;a为参考椭球的长半轴,实际计算时取相对于GRS80的值;Cnm、Snm为完全规格化位系数,其中偶次带谐系数代表实际引力位与正常引力位的系数之差;Pnm(sinφ)为完全规格化Legndra函数,当模型的阶次很高时需注意算法的稳定性;N为地球重力场模型展开的最高阶数。
1.3.2 残余高程异常计算
根据计算得到的EGM2008重力场模型异常及已知GPS/水准点高程异常计算残余高程异常:
ξ残余=ξ模型-ξGPS/水准.
(5)
1.3.3 拟合计算
根据计算得到的残余高程异常,使用最小二乘原理计算二次曲面模型参数,得到残余高程异常拟合模型。根据残余高程异常拟合结果及EGM2008重力场模型高程异常进行GPS高程转换,将大地高转换为正常高。
2 算 例
2.1 项目概况
新疆地区某控制测量项目,测区人烟稀少,交通不便,地形以荒漠、戈壁滩为主,自然环境恶劣,平均海拔约1 300 m,地势较平坦。测区东西长约260 km,南北约230 km. GPS/水准点点位分布情况如图1所示。

图1 控制点点位分布图
2.2 拟合方案
图1中控制点均有高精度的水准高及大地高,根据已有数据进行高程拟合,拟合方案有三种:
方案1:不使用已知GPS/水准点数据,只根据Bruns公式,使用EGM2008地球重力场模型进行GPS高程拟合,拟合方法见文献[1]。
方案2:只根据已知点使用二次曲面拟合法,采用最小二乘法计算模型的拟合系数,进行高程拟合,拟合方法见文献[7]。
方案3:使用Bruns公式计算EGM2008重力场模型高程异常,并根据公式(5)计算残余高程异常,采用二次曲面拟合残余高程异常,根据残余高程异常拟合结果及EGM2008重力场模型高程异常将大地高转换为正常高。
拟合后使用检查点进行精度检查,并以检查点高程为真值,计算中误差,结果如表1所示。
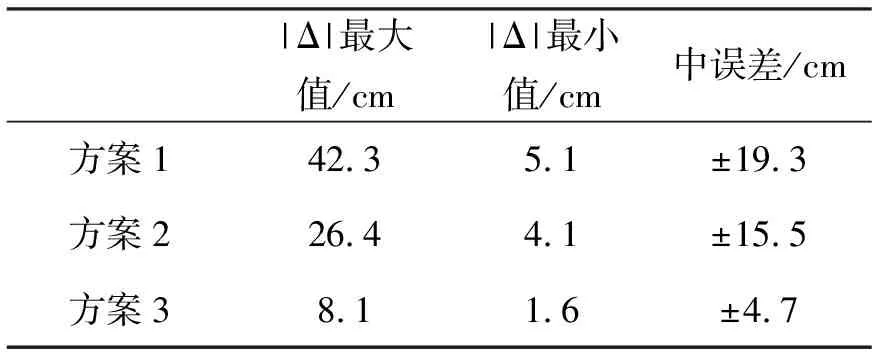
表1 GPS高程拟合精度检查表
从表1可以看出,方案3的拟合精度明显高于方案1、方案2.
2.3 精度分析
1) 方案1:方案1 GPS高程拟合的精度主要取决与EGM2008地球重力场模型的高程异常精度。根据文献[6]的研究结果,EGM2008地球重力场模型在内地的总体精度为20 cm,但表现出明显的区域不平衡性,华东华中地区12 cm,华北地区达到9 cm,西部地区,EGM2008地球重力场模型的精度为24 cm.方案1拟合结果与文献[6]相符。
2) 方案2:由于测区范围较大,约60 000 km2,GPS/水准点相对较少,且分布不均匀(测区中部缺少控制点),方案2的GPS高程拟合中误差为±15.5 cm,相对方案1精度有所提高,但并不明显。
3) 方案3:方案3顾及了GPS高程拟合中地球重力场的影响,同时采用高精度GPS/水准数据,计算得到残余高程异常,并使用二次曲面模型对残余高程异常进行了拟合。该方法既考虑了地球重力场因素,又利用GPS/水准数据消除了EGM2008地球重力场模型与我国高程基准的系统性偏差,GPS高程拟合中误差为±4.7 cm,精度明显高于方案1、方案2,是最优方案。
3 结束语
由于单一模型的GPS高程拟合方法忽略了地球重力场的影响,需要数量足够、位置分布合理的高精度GPS/水准点才能获得较高的拟合精度。根据EGM2008重力场模型求解高程异常精度只能达到分米级,不能直接用于生产实践。顾及EGM2008地球重力场模型,使用二次曲面法进行GPS高程拟合,既考虑了重力场因素,又使用GPS/水准数据消除了EGM2008地球重力场模型与我国高程基准的系统性偏差,只需较少控制点拟合即可达到厘米级精度。
由于测区地形相对简单,地势较平坦,且检查点未能完全反应整个测区的精度,更大范围、地形复杂区域的顾及EGM2008重力场模型的GPS高程拟合需要进一步探讨。
[1] 张兴福,刘成,王兵海,等.无水准数据的GPS高程转换方法及精度分析[J].大地测量与地球动力学,2010,30(1):114-118.
[2] 杨建辉.多面函数法在确定局部似大地水准面中的应用研究[J].全球定位系统,2011,(4):65-68.
[3] 李爱国,王卫,徐永胜.BP神经网络在局部似大地水准面精化的应用[J].全球定位系统,2008,(3):29-31.
[4] 陈 淋.PSO-RBF在似大地水准面精化中的应用[J].全球定位系统,2013,38(4):53-55.
[5] 蔡庆立,卢 荣.EGM2008重力场模型在RTK高程测量中的应用[J].全球定位系统,2012,37(4):71-73.
[6] 章传银,郭春喜,陈俊勇,等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009,38(4):283-288.
[7] 蔡庆立.基于二次曲面拟合的区域似大地水准面确定[J].矿山测量,2011,(4):24-25.

