基于信号模拟器的接收机抗干扰测试方法研究

郝燕玲,梁 宏,周广涛

(哈尔滨工程大学自动化学院，黑龙江 哈尔滨 150001)

0 引 言

随着GPS系统配置的日趋完善，卫星导航技术已渗透到国民经济和社会生活的各个方面，并且正发挥着越来越重要的作用。然而，相比于其他导航方式，如惯性导航或天文导航，卫星导航系统的非自主性便成为导航定位干扰的最佳入手点。在复杂电磁环境下对卫星导抗干扰接收机的抗干扰能力进行测试与评估，对提高我国卫星导航系统在实际应用环境下的安全性与可靠性具有重要的意义[1]。抗干扰能力是卫星导航接收机重要的性能指标之一，因此对于导航定位接收机抵抗干扰能力的测试和鉴定便成为下一步卫星导航接收机发展的重中之重。目前的国内测试标准中尚未对接收机抗干扰测试性能进行明确的规定，同时，现阶段的抗干扰测试技术对干扰性能的评价没有统一的标准[2-4]。本文提出了一种对接收机抗干扰性能的测试方法，经过计算机仿真实验的验证，证明可以有效地评估接收机的抗干扰性能，为未来卫星导航接收机的性能测试提供值得借鉴的参考。

1 干扰信号类型及特性

根据干扰的作用原理进行划分，卫星信号的干扰可分为压制式干扰和欺骗式干扰[5]。

压制式干扰是GPS接收机面临的重要威胁之一，对伪码跟踪的跟踪精度产生影响，甚至导致伪码跟踪环失锁[6]。通常模拟的压制式干扰包括宽带高斯噪声干扰、窄带干扰、连续波干扰和锯齿调频波干扰等。

欺骗式干扰主要指:利用与真实信号类似的干扰信号，使通信系统接收方不易察觉到干扰信号的存在，把干扰信号当成有用信号进行解调，提供给接收方错误的信息[7]。大部分采取的干扰方案是先进行大功率的压制式干扰，使得接收机无法接收到正常的信号，在压制式干扰信号撤销之后，紧随其后的是欺骗式干扰，如转发式的伪卫星信号，并且通过渐变的手段进一步干扰接收机的判断。

本文将对几种典型的压制式干扰信号进行重点分析。

1.1 窄带干扰

最常用的，也最易获得的压制式干扰信号就是高斯白噪声，随着干扰信号功率的增加，误码率也逐渐增大。当误码率达到一定程度时，就可以切断其通信链路。不难想象系统在受到窄带高斯白噪声干扰时，系统误码率与接收机末端的干扰功率有关，干扰功率越大，误码率越高，反之则越小。而误码率又是衡量对系统干扰效能的最重要的指标。

由于系统扩频增益的存在，会造成干扰功率的极大损失，使得接收机末端干扰功率所剩无几。同时又受到硬件条件的制约，不可能无限制的增大干扰机的输出功率。因此，研究干扰信号在怎样的条件下，经扩频增益后接收机末端输出功率最大是一个关键问题[8]。

设窄带干扰信号的功率均匀分布在其带宽内，并且其功率为Pj，基带信号n(t)的带宽为[-Mfd,Mfd]，其中M定义为干扰信号的相对带宽，则干扰信号的功率谱为

(1)

干扰信号进入接收机后，进行相关解扩。假设接收机的本地扩频码已经和发射端扩频码同步，并且本地载波也和有用信号同频。

接下来推导干扰信号的输出功率，已知两个相互独立的信号在时域上的乘积，相当于其功率谱密度在频域上的卷积。另外，由于累加器的幅频特性，在频域上，累加清除器相当于一个低通滤波器，并且累加清除器的累加长度的大小，关系到低通滤波器性能。该低通滤波器的通频带宽度等效为[-fd,fd]

有了以上两点结论，可以从频域的角度进行分析，干扰信号在接收机末端，落入接收机通带内的平均功率σ2为。

(2)

以m序列的PRN码为例，PRN码的功率谱为

(3)

如果定性地分析，在频域上，PRN码和干扰信号相卷积后通过低通滤波器，其截止频率为fd.根据PRN码的功率谱密度表达式和干扰信号的功率谱可以看出，窄带高斯白噪声信号和PRN码卷积的过程就相当于将干扰信号频谱中心位置搬移到PRN码的每一个谐波频点处进行加权，加权值就是PRN码在该频点处的功率谱大小。而卷积后落入低通滤波器内的能量的总和就等于干扰信号在接收机末端的能量。

因此，当信号带宽较窄时，卷积后的高次谐波分量无法落入低通滤波器的通带内，能量损失。增大信号带宽，虽然可以利用高次谐波分量，但是由于干扰功率为定值，干扰信号的功率谱密度随之减小，并且高次谐波分量的加权值也较小，最终落入低通滤波器带内的能量不一定会持续增大。由此可以定性的判断存在一个最佳带宽，使得在利用高次谐波和获得较大干扰信号功率谱值之间找到一个折中点，而这个带宽值，就可以认为是对于该信号最佳的窄带干扰带宽。

将式(1)和式(3)带入式(2)，并且根据fc/fd=N，可以得到

(4)

由上式可以看出，干扰信号在接收机末端的输出功率和干扰信号的输入功率、干扰信号相对带宽M以及接收机所采用的扩频码m序列的周期N有关。对于一部接收机一般采用固定阶数的m序列作为扩频码，那么扩频码N=2r-1为一个定值。在干扰信号输入功率一定的条件下，干扰信号输出功率仅与干扰信号的带宽有关。当Pj=1 W，以10阶的m序列N=210-1=1 023为例，根据上述可以得到干扰信号输出功率与相对带宽M的关系，正如前面理论分析的一样，干扰信号输出功率并不是呈现单调的变化趋势，而是存在一个最大值，即存在一个最佳带宽，使得干扰信号输出功率最大。对于N=1 023，最佳相对带宽M=62.

同样，可以对不同阶数的m序列做出同样的分析，并计算出相应的最佳相对带宽值，如表1所示。

表1 最佳相对带宽

1.2 单频干扰

由于单频干扰的频率成分中只有单一的频率，因此无法使用功率谱密度来计算接收端的功率。对C/A码接收机，收到GPS信号可表示为

N(t)+J(t),

(5)

式中:P为接收功率；D为数据信号；CA为信号C/A码；N(t)为高斯噪声；J(t)为单频干扰信号。

经过相关解调和码同步解扩并积分后，信号变为

Z=Z0+η+ζ,

(6)

式中：

φ)CA(t)cos(ω1t+φ)dt，

其中，Tb为一个数据码的周期。Z0的值为

(7)

式中，D表示信号的数据码。

对于频率和相位一定的单频信号，ζ是确定值。当计入高斯噪声时，如果Z0>0，则当η<-(Z0+ζ)时出现判决错误，如果Z0<0，当η>-(Z0+ζ)时出现判决错误。而+1和-1出现的概率相等，根据改进的高斯近似，估计的误码率为

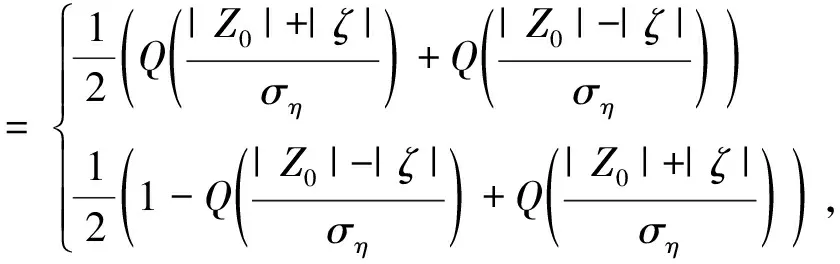
(8)

式中，

(9)

可知，单频干扰的效果取决于干扰信号的频率和相位，而相位具有随机性，因此在计算误码率时需对不同相位的误码率求平均。假设信干比和信噪比都取为30 dB.可以得到当干扰信号频率正对载波频率时，干扰效果并不好，当干扰信号取一定频偏时可取得最佳干扰效果。计算表明单频信号对GPS的最佳归一化干扰频偏为士0.096.

1.3 锯齿波干扰

锯齿调频波的频率和相位表达式为

(10)

t0,tm)]2}-πfmmod(t-

t0,tm)+φ0,

(11)

其中:f0为中心频率；fm为频率调制范围的大小；tm为调频周期；t0为初始时刻；φ0为初始时刻相位；mod(m,n)给出m除以n后的余数,如图1所示。

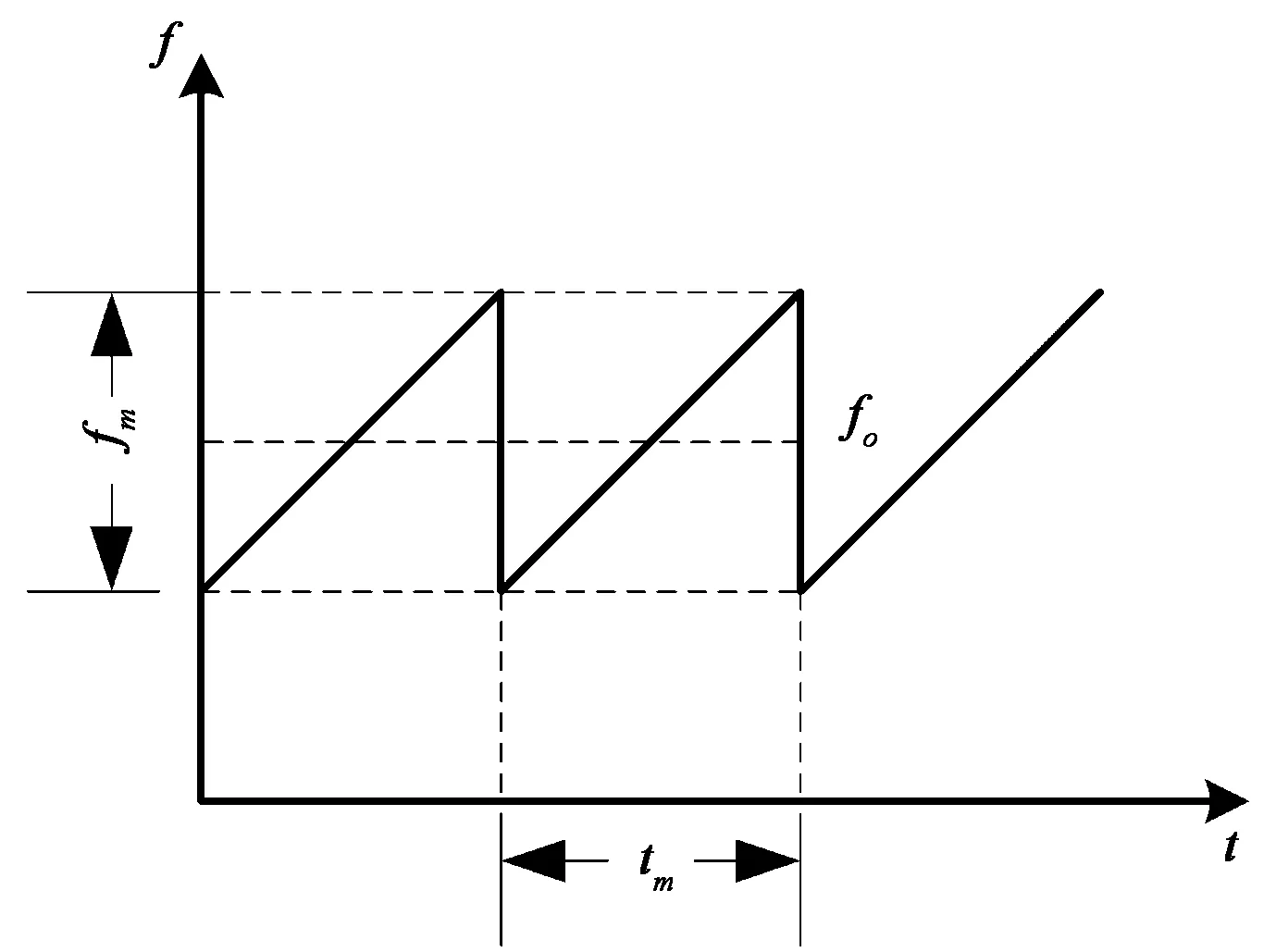
图1 锯齿调频波频率分布

由锯齿调频波的表达式可知，信号中各个频点的成份权重相同，即相应的信号功率谱密度可以认为均匀分布在调频范围之内，由此，可以参照窄带干扰性能的结论。

2 接收机抗干扰测试

本文主要针对导航定位接收机进行抗干扰性能的测试，因此将整个接收机看作整体，以卫星信号为输入，将接收机的导航定位结果作为输出，考察接收机的抗干扰性能。其中将考察的重要指标包括：

1) 抗干扰灵敏度：接收机的抗干扰灵敏度定义为接收机能够正常工作时对应的接收机输入端的最小信噪比(或载噪比)。抗干扰灵敏度是干扰类型、干扰强度和接收机性能等多个参量的函数，显然,接收机抗干扰灵敏度数值越小，接收机越灵敏,说明接收机的抗干扰能力越强。

2) 干扰抑制度：接收机的干扰抑制度定义为接收机能够正常工作时所对应的接收机输入端的最大干噪比。干扰抑制度反映了信号环境一定时,在接收机的性能满足要求条件下, 接收机对干扰信号的最大抑制能力。显然,干扰抑制度越大,接收机的抗干扰能力越强[6]。

抗干扰灵敏度和干扰抑制度从不同侧面反映接收机的抗干扰能力：抗干扰灵敏度是在一定的干扰环境下,考察接收机对有用信号的要求；干扰抑制度是在一定的有用信号条件下,考察接收机对干扰信号的容忍能力。二者都是在使接收机达到最低性能要求的约束下定义的[9]。利用抗干扰灵敏度和干扰抑制度两个抗干扰性能评估参量,可有效地评价接收机的抗干扰性能。

3 仿真实验及结果

使用实验室自行研发的GPS信号模拟发生器产生数字仿真信号，对实验室自行研发的GPS软件接收机进行测试，先对不同类型的干扰信号进行了仿真验证，再按照仿真信号的信噪比以及干扰信号的强度即干噪比不同，分别设计仿真实验条件，最后绘制抗干扰性能曲线。

3.1 不同类型干扰信号

模拟器设定为静态输出，但是在产生中频信号的过程中，对中频信号添加干扰。添加的干扰类型包括窄带干扰、连续波干扰、锯齿调频波。接收机对添加干扰后的中频信号分别进行GPS单独解算。接收机的相干积分时间是1 ms.干扰的干信比J/S为40 dB.选取PRN号为10的可见卫星作为跟踪对象，通过解算过程中的载波的多普勒频移来反映添加的干扰对接收机跟踪性能的影响。仿真时，在信号接收过程中500～600 ms处添加干扰。

按照前文分析的窄带干扰的最佳带宽设置，此处对信号添加62f0的干扰信号，其中f=1.023 MHz.按照前文分析的单频连续波干扰的最佳频率设置，此处对信号添加的fI+0.096×fI干扰信号，其中fl为信号的中心频率。结果如图2、3所示。

图2 窄带干扰多普勒频移

图3 单频干扰多普勒频移

对中频数据添加锯齿调频波干扰。图4示出了GPS单独解算时的多普勒频移的跟踪结果。

图4 锯齿波多普勒频移

如图4所示，此处直接列出最佳的干扰效果图。从图中可以看出，添加干扰信号后，相应的多普勒频移将会出现振动频率增大、振动幅值增大等现象。分析其原因，当添加干扰后，相当于增加了噪声的强度，即降低了有用信号的信噪比，从而将会影响接收机的跟踪环路性能。理论与实测结果一致，同时验证了前文所设计的干扰信号类型。

3.2 不同信噪比的仿真信号

固定干扰信号的强度，改变信号的信噪比来测试接收机灵敏度。此处给出在不添加任何干扰信号的环境下，接收机的测试结果。如图5所示。

图5 灵敏度测试结果

测试过程采用不添加干扰信号，仿真信号的载噪比设计成每1 000 ms降低1 dB，直至导航接收机的静态定位误差超出定位精度的2倍时，认为接收机已经无法正常工作，此时的仿真信号信噪比就是接收机的抗干扰灵敏度。

从结果图中可以看出，当有用信号的载噪比不断降低的时候，接收机的定位误差将逐渐增大，误差的波动范围和频率都会相应增大，当信噪比降低到使得接收机环路跟踪误差超过门限值时，接收机环路失锁，无法正常工作。理论分析与仿真测试的结果一致。

3.3 不同干噪比的仿真信号

固定仿真信号的载噪比，改变干扰信号的强度，即改变信号的干噪比，从而得到接收机的干扰抑制度。此处采用45 dB信号环境，测试结果如图6所示。

测试过程中，保持信号载噪比不变，每隔1 000 ms增加干扰信号的强度，图示结果为窄带干扰测试结果。直至接收机无法正常工作，此时的干扰信号的干噪比即为接收机的干扰抑制度。

从结果图可以看出，当干扰信号的强度不断增大时，接收机的定位偏差逐渐增大，且相应的波动范围及频率也同时增大，与理论分析结果一致。

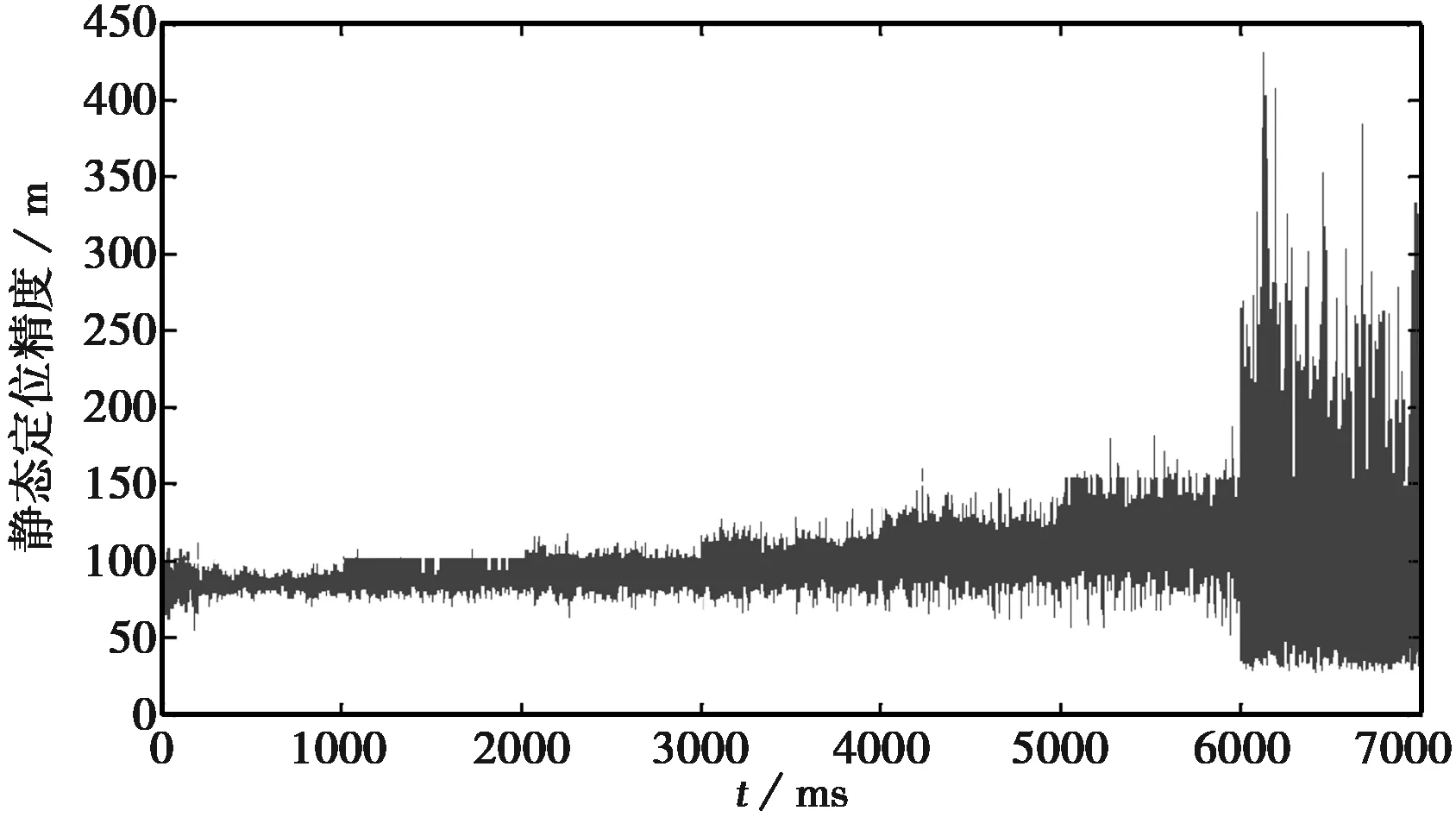
图6 干扰抑制度测试结果

3.4 抗干扰性能曲线

为了对比接收机的抗干扰性能，可以对接收机分别进行灵敏度和干扰抑制度的测试，如针对不同的有用信号强度，即载噪比，测试出不同的干扰抑制度，绘制出关于灵敏度和干扰抑制度的曲线图，可以更加直观的比较出接收机抗干扰性能的优劣。

通常情况下接收机抗干扰性能曲线并不一定是单调的。并且对于同一个接收机而言,不同干扰类型下的抗干扰性能曲线一般不会完全一致,也就是说,接收机对不同类型干扰的抑制能力是不一样的。本文将给出窄带干扰情况下的仿真测试结果。

采用单独的GPS解算与有环路的惯导深组合方式进行对比，相应的仿真测试条件便不能继续选用静态定位，具体条件如表2所示。

表2 仿真测试条件

根据上表所列仿真条件进行测试，可以得到单独GPS解算以及惯导辅助的GPS组合解算结果，图7示出了抗干扰曲线。

从图7中可以看出，当接收机使用惯导辅助导航定位后，在相同的有用信号强度下，接收机对于干扰信号的干扰抑制度明显增加，可以说抗干扰的能力增强；另一方面，使用惯导辅助导航后在相同的干扰环境下，接收机的导航定位灵敏度也有明显的增强，如图8所示，因此，可以说，GPS-INS深组合导航接收机的抗干扰性能比单独GPS接收机好，理论与实验结果相符。

图7 不同接收机的抗干扰度对比

图8 不同接收机的灵敏度对比

4 结束语

本文从信号的接收原理入手，对导航定位接收机的干扰信号进行了分析，尤其对几种典型的压制式干扰信号进行了详细推算，找到了相应的最佳干扰形式，并且通过软件仿真实验对其进行了验证。可以为其他相关的接收机测试做前期准备工作。

同时，阐述了一种接收机抗干扰性能的评价方案，并且利用软件的模拟信号发生器及GPS软件接收机进行了仿真实验，从不同的角度评价了实验中所使用的两种接收方案的抗干扰性能，实验结果与理论分析一致，实验验证正确。

[1] 吴 俊. GPS信号和干扰仿真系统的设计与实现[D].合肥：国防科学技术大学,2008.

[2] 张 宁,张 霞,朱太平. 基于波束形成天线抗干扰接收机的测试研究[J]. 电子设计工程,2013,10:69-72.

[3] 郭淑霞，张 宁，刘孟江，等.一种卫星导航抗干扰接收机的室内无线测试方法[J]. 计算机工程与科学，2013, 35(7): 169-174.

[4] 刘思睿. GNSS 接收机性能综合测试技术研究[D].北京：北京化工大学，2013.

[5] RAPPAPORT T S. Wireless Communications Principles and Practice[M].2版.北京：电子工业出版社，1999:414-430

[6] 汤俊杰,薛 磊,林 航,等. 压制干扰对GPS接收机码跟踪环的性能影响分析[J]. 信息技术,2011,03:68-71.

[7] 刘雪松. 混沌扩频通信系统及其干扰技术研究[D].成都：电子科技大学,2009.

[8] 肖曼琳. 直扩通信系统的干扰效能评估与仿真[D].成都：电子科技大学,2006

[9] 李树洲,桑怀胜. 卫星导航接收机抗干扰性能评估方法研究[J]. 无线电工程,2006(9):37-41.