基于线性扩张状态观测器的平行泊车路径跟踪*

王健 赵又群† 季学武 刘亚辉 臧利国

(1.南京航空航天大学 能源与动力学院，江苏 南京 210016;2.清华大学 汽车安全与节能国家重点实验室，北京 100084)

随着世界汽车工业的飞速发展，汽车产销量的快速增长与可利用泊车空间的日益减少之间的矛盾变得日益突出.在拥挤的城市街道，泊车变得越来越困难，特别是对于没有经验的驾驶员来说，泊车更加困难［1］.为了提高驾驶舒适性和安全性，开发智能泊车辅助系统迫在眉睫.智能泊车辅助系统能够利用超声波传感器和摄像头感知、识别车辆路径信息，通过控制电动助力转向系统进行转向操作来实现有效泊车.采用该系统，泊车时驾驶员只需控制好油门和刹车即可，大大减轻了驾驶员的负担.

路径规划和路径跟踪是平行泊车理论研究中的两个关键部分.在路径规划方面，国内外学者进行了大量研究，研究中多采用两段圆弧相切的方法，设计的圆弧需要满足避障约束条件［2-5］.为了解决路径曲率不连续问题，有研究者采用了B 样条曲线、Bezier曲线拟合、多项式曲线拟合、回旋曲线拟合和β 样条曲线拟合等方法［6-8］.路径规划好之后，路径跟踪的准确与否直接决定了平行泊车是否成功.Zhao 和Ollero等［9-10］采用模糊控制方法设计了路径跟踪控制器，通过超声波传感器实时检测车辆与泊车位之间的位置关系，据此决定方向盘的转角大小.Demirli 等［11］设计了自适应模糊控制路径跟踪控制器来控制车辆的跟踪参考路径.在Lian 等［12］采用模糊滑模控制方法设计的控制器中，将驾驶员经验考虑进了模糊控制模块，控制力的大小通过模糊控制进行调节，其方向则由滑模控制决定.上述方法均基于现代控制理论来设计控制器，但存在以下不足:难以制定准确的模糊控制规则，模糊控制和滑模控制的工程应用困难.为解决上述问题，文中基于线性扩张状态观测器(LESO)设计路径跟踪控制器.该观测器不需建立被控对象的精确数学模型，结合了经典控制理论和现代控制理论的优点［13-14］.LESO 可以将系统存在的干扰和模型不确定性观测出来并补偿掉，因此可有效提高系统的鲁棒性.

1 平行泊车系统描述

平行泊车系统主要由以下几部分组成:位于前保险杆两侧的两个超声波传感器、1 个电子控制单元、1个方向盘角度传感器、1 套电动助力转向系统、4 个轮速传感器和1 个人机交互界面.基于铃木北斗星汽车(样机)开发的平行泊车系统结构如图1 所示.

图1 平行泊车系统的结构Fig.1 Structure of parallel parking system

2 路径规划

2.1 车辆运动学模型

车辆运动学模型越精确，越能够真实反映车辆的运动情况.在泊车速度较低、车辆后轮与地面之间满足纯滚动约束、后轴中心速度v 垂直于后轴的条件下，以车辆后轴中心为参考位置，建立图2 所示的车辆运动学模型.

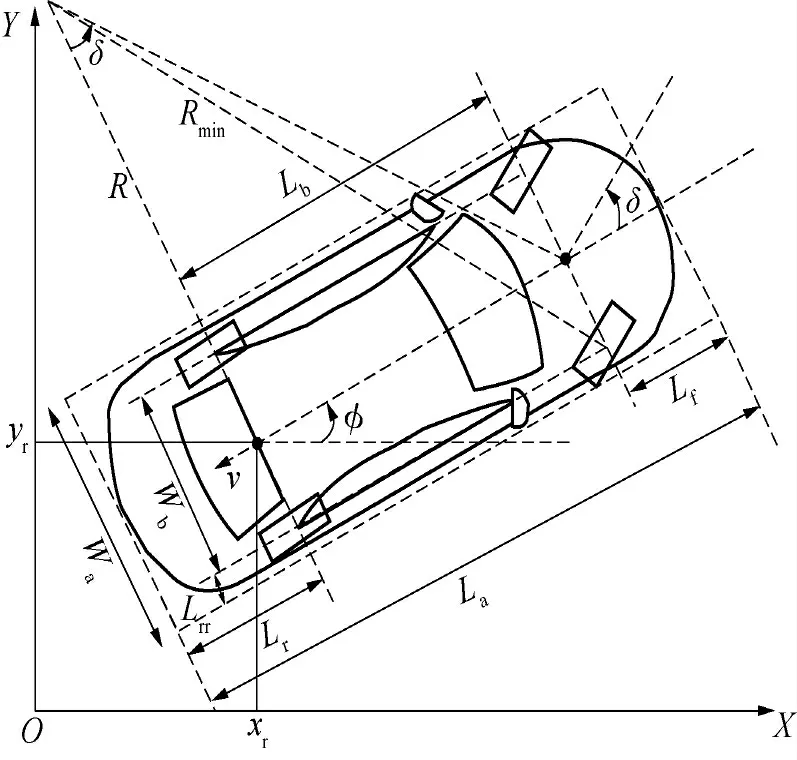
图2 车辆运动学模型Fig.2 Kinematics model of vehicles

考虑外界干扰和建模不确定性，建立以后轴中心为参考点的车辆运动学方程如下:

式中，v 为车辆后轴中心速度，f(v，t)为由于路面颠簸引起的外界扰动，ws(v，t)为由转向机械机构复杂性引起的转向运动学建模不确定性，δ为前轴中心转角，Ts为转向系统延迟时间，u 为前轴中心转角控制量，其他变量的定义如图2 所示.

2.2 参考路径

图3 所示为平行泊车路径，由一段直线(S0)和两段圆弧(S1、S2)组成.建立平行泊车过程的方程如下:

式中，R1、R2、S0、θ 和h0等参数的定义如图3 所示.泊车终止点目标位置由Drl、Dlo和Drr三个安全距离参数限定，如图4 所示.

图3 平行泊车路径Fig.3 Parallel parking path

图4 目标位置限定Fig.4 Goal position constraint

车辆驶离车位的过程中，车身的右前方要躲避前方障碍物，设安全距离为Dfr，根据图4，可以计算出转弯半径R1的最大值，如下所示:

式中，Lp为超声波传感器检测到的有效泊车位长度，Lr为后悬长度，La为车身长度，Lrr为车辆后轮中心平面到车身外沿的长度，Wa为车宽，Wb为后轮轴距.受车辆本身最小转弯半径Rmin的限制，R1的最小值为

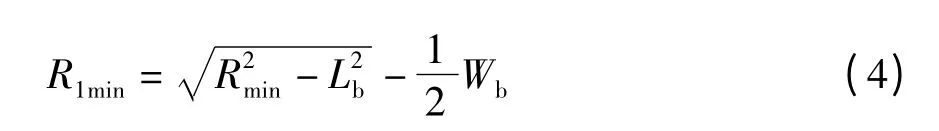
式中，Lb为车辆轴距.R1的取值范围如下:

图5 和6 为泊车过程中可能发生碰撞的位置.由图5 和6 可以计算出转弯半径R2 的最大值和最小值.具体计算过程可由式(5)和(6)描述:

式中，(m1，n1)和(m2，n2)分别为圆心O1和圆心O2的坐标，Δy 表示侧向超声波传感器到马路沿的距离，(Cx，Cy)表示前方障碍物左后端位置坐标.

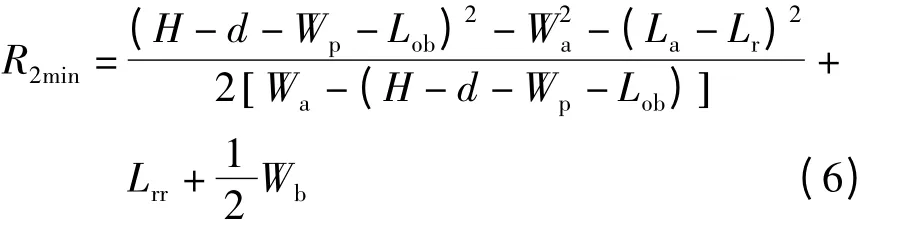
图5 第二碰撞位置Fig.5 The second collision position

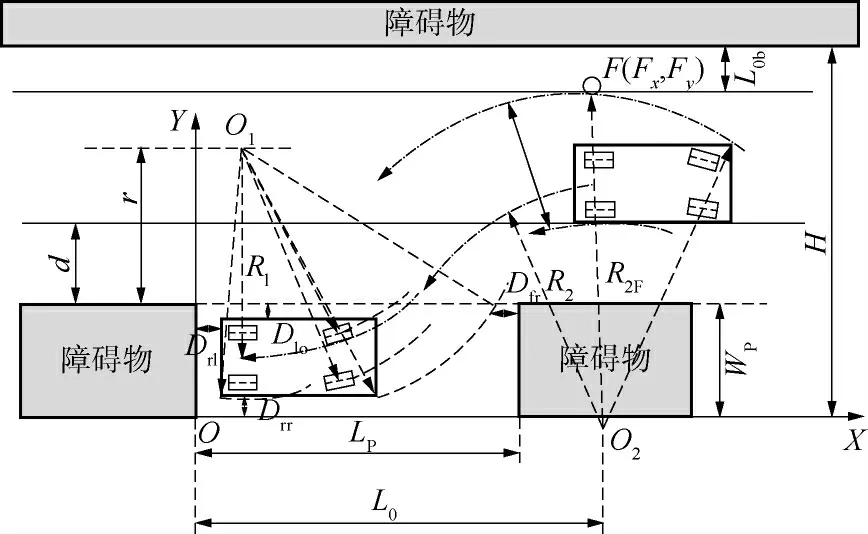
图6 第三碰撞位置Fig.6 The third collision position

式中，H 为左侧障碍物与马路沿之间的距离，d 为侧面超声波传感器与右侧障碍物之间的距离，Lob为车头左前方距左侧障碍物的安全距离.

R2的取值范围如下:

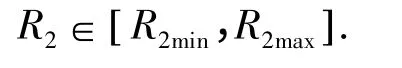
最近泊车起始位置和最远泊车起始位置可以表示为

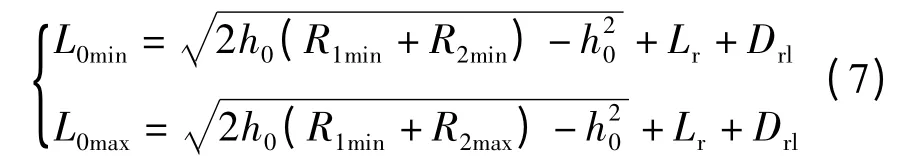
上述方法规划的路径曲率不连续，为了满足曲率连续这一约束条件，并且使规划的路径能够满足转向执行机构的要求，采用三次B 样条曲线对规划的泊车路径进行曲线拟合.限于篇幅，文中对曲线拟合部分不展开描述，最终规划的泊车路径曲线如图7 所示.

图7 泊车路径Fig.7 Parking paths

3 线性扩张状态观测器

3.1 线性扩张状态观测器的相关理论

线性扩张状态观测器可以将系统所受到的外界干扰和建模不确定性部分观测出来并补偿掉，保证系统的鲁棒性.它将系统受到的外界干扰和未建模部分看作一个新的状态——扩张状态，通过输出反馈的方式观测这个状态［15］.对于单输入单输出非线性时变系统，

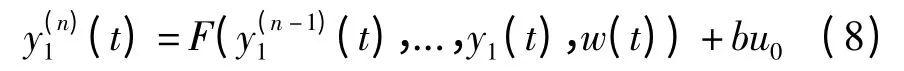
式中:y1和u0分别表示控制输出和控制输入;F(t)，...，y1(t)，w(t))表示非线性时变未知动态，包含系统的内部动态和外部干扰w(t)，为方便描述，把它简记为F，w(t)可以是时变的，也可以是定常的;b 为未知的控制增益系数，通常可以根据具体系统求解其范围，亦可以粗略估计，取b0≈b.方程(8)可重新定义为

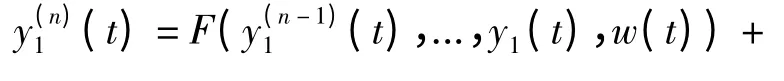
通过上述转化，将非线性系统转化成线性系统的状态方程形式，从而构造线性扩张状态观测器，实时估计出被扩张的状态量.其中，扩张状态观测器的一般形式为

［z1z2… zn+1］T是扩张状态［x1x2… xn+1］T的估计值，［l1l2… ln+1］为设计参数.

3.2 线性扩张状态观测器的设计

平行泊车系统可以看作二阶系统，采用三阶扩张状态观测器进行未知建模和外界干扰的观测估计.考虑车辆运动学方程

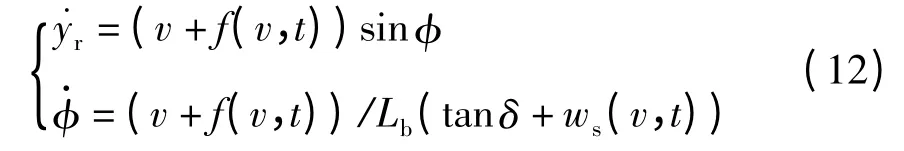
平行泊车路径跟踪模型可以认为是包含yr和φ 两个参数的二阶系统，令x1=yr，则系统性扩张状态方程如下:

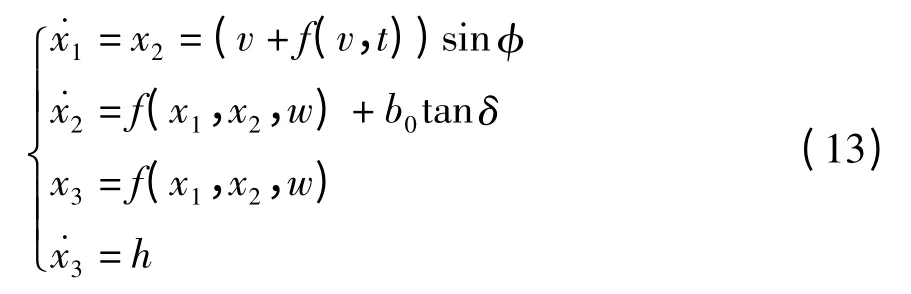
文中将预瞄跟随理论应用于平行泊车路径跟踪过程［16］，如图8 所示.控制器的控制目的是让车辆跟随理想参考轨迹，即控制侧向位移误差Δy 趋近于0.图8 中，L 表示预瞄距离，T 表示预瞄时间，泊车过程中车速较低，预瞄时间可以取固定值，仿真中T 取0.5 s.其中，侧向位移误差Δy 可以表示成

式中，(x0，y0，φ0)为车辆当前时刻的位置和偏航角度，vx和vy表示纵向速度在水平和垂直方向的分量，f(x)表示参考路径.

图8 预瞄跟随Fig.8 Preview follower

所设计的平行泊车路径跟踪控制器如图9 所示.为了便于工程应用，将线性扩张状态观测器写成离散形式.三阶线性扩张状态观测器的离散形式如下所示:

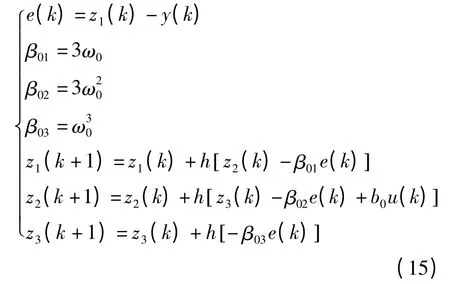
式中，ω0是由极点配置得到的线性扩张状态观测器的带宽.

图9 路径跟踪控制器Fig.9 Path tracking controller

线性组合离散表达式为

式中，ωc为期望的闭环系统带宽，一般情况下取ω0=(5～10)ωc.为了消除外界干扰和模型不确定性干扰，实际输入到执行机构的控制量u 可以表示为

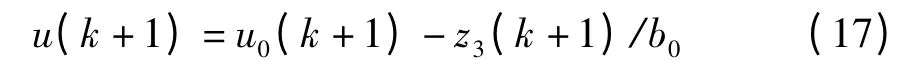
4 仿真与实车测试

4.1 仿真结果及分析

考虑泊车时的路面颠簸，外界干扰量对泊车速度的影响量f(v，t)可以表示成车辆纵向速度v和时间t 的函数，即f(v，t)=vsin(8t).考虑转向系统运动学建模的不确定性，此时，ws(v，t)=0.02v·sin(5t).转向系统延迟作为系统内部干扰量进行处理，延迟时间Ts=0.5 s.将仿真结果与采用传统PID控制器进行的路径跟踪效果进行对比，以验证文中建立的控制器在解决平行泊车路径跟踪时的有效性和鲁棒性.线性扩张状态观测器的相关参数如下:b0=1.6，ω0=140，ωc=20.PID 控制器参数采用最优方法优化如下:Kp=2，Ki=0.5，Kd=1.泊车速度曲线如图10 所示，其中车辆纵向速度v=1 m/s.基于线性扩张状态观测器设计的路径跟踪控制器与PID 控制器的路径跟踪效果对比如图11 所示.

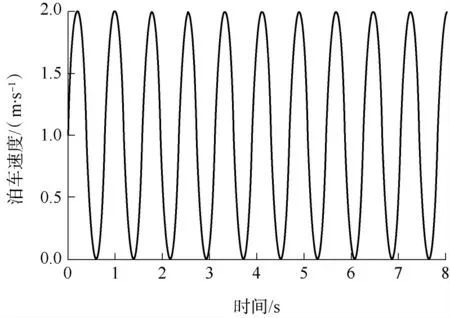
图10 仿真设定的泊车速度Fig.10 Simulation parking speed

图11 仿真环境下的路径跟踪效果对比Fig.11 Path tracking comparison in simulation environment

从图11 可以看出，基于线性扩张状态观测器的路径跟踪效果优于PID 控制效果.其中，线性扩张状态观测器观测出的系统总扰动量如图12 所示.在不改变控制器参数的情况下，试验测得的泊车速度如图13 所示，路径跟踪效果对比如图14 所示.泊车末端PID 控制器不能很好地控制车辆跟踪的理想路径.线性扩张状态观测器的控制效果优于PID 控制器的原因在于，前者能够观测出外界干扰和模型不确定性，如图15 所示.

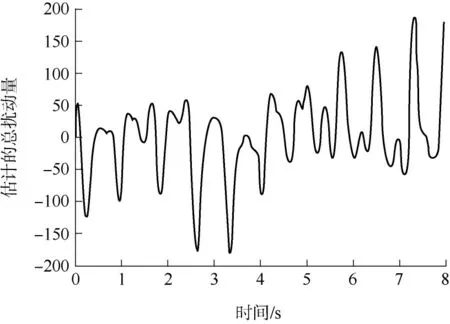
图12 仿真环境下估计的总扰动量Fig.12 Estimated total disturbance in simulation environment

图13 试验测得的泊车速度Fig.13 Parking speed measured in experiment

图14 试验环境下的路径跟踪效果对比Fig.14 Path tracking comparison in experiment environment

图15 试验环境下估计的总扰动量Fig.15 Estimated total disturbance in experiment environment

4.2 实车测试结果及分析

为了验证文中路径跟踪控制算法的有效性，进行了实车验证.将所开发的平行泊车系统安装在铃木北斗星汽车上，进行路径跟踪测试.采用上海司南导航公司开发的差分GPS 进行车辆实时位置数据采集.其中，基站和移动站型号分别为M300 和M600 系列，该差分GPS 同时支持GPS 和北斗系统，位置定位精度为1 cm，偏航角精度为0.1°，数据更新速率为10 Hz.试验中对车辆实际运行轨迹进行数据采集，并与规划的理想泊车路径进行对比，结果见图16.

图16 实车试验数据Fig.16 Real vehicle experiment data

实车试验中，车位大小由侧方超声波传感器测得，车位长度为6 m，宽度为2.5 m.为了计算整个泊车过程中侧向位移误差的平均值，在理想路径和实际路径上随机取10 个路径点计算其侧向位移误差，结果见表1.通过计算相同位置X 处的理想泊车轨迹纵向位移Yideal和实车测试得到的泊车轨迹Yactual，可以计算出最大侧向位移误差为0.111 m，平均误差为0.0677 m，说明利用文中的路径跟踪算法可以控制车辆无碰撞地实现平行泊车.

表1 侧向位移误差Table 1 Lateral displacement error

5 结语

文中考虑路面颠簸、转向系统运动学模型的不确定性以及转向系统的延迟，建立了平行泊车运动学模型，并设计了基于线性扩张状态观测器的平行泊车路径跟踪控制器.该跟踪控制器能够将模型不确定性以及外界干扰作为一个总的扰动量，通过线性扩张状态观测器将其观测出来并补偿掉，保证了系统的鲁棒性.仿真结果表明，基于线性扩张状态观测器设计的路径跟踪控制器的控制效果优于传统PID 控制器，且其工程实现简单，观测器参数具有鲁棒性;而PID 参数需要根据不同工况不断调整，适应性较差.实车试验结果表明，基于线性扩张状态观测器设计的路径跟踪控制器能够精确控制车辆完成平行泊车任务，最大误差仅为0.111 m.文中提出的路径跟踪方法可以应用到智能驾驶领域，能够提高车辆高速行驶并且受到外界干扰时的路径跟踪鲁棒性，为实现车辆真正的无人驾驶打下了基础.

［1］Huang S J，Lin G Y.Parallel auto-parking of a model vehicle using a self-organizing fuzzy controller［J］.Proceedings of the Institution of Mechanical Engineers(Part D):Journal of Automobile Engineering，2010，224(8):997-1012.

［2］Mukherjee R，Anderson A.A surface integral approach to the motion planning of nonholonomic systems［J］.Journal of Dynamic Systems，Measurement and Control，1994，116(3):315-325.

［3］Laumont J P，Jacobs P E，Taix M，et al.A motion planner for nonholonomic mobile robots ［J］.IEEE Transactions on Robotics and Automation，1994，10(5):577-593.

［4］Jiang K，Seneviratne L D.A sensor guided autonomousparking system for nonholonomic mobile robots ［C］∥Proceedings of 1999 IEEE International Conference on Robotics and Automation.Detroit:IEEE，1999:311-316.

［5］吴冰，钱立军，虞明，等.基于RBF 神经网络的自动泊车路径规划［J］.合肥工业大学学报:自然科学版，2012，35(4):459-463.Wu Bing，Qian Li-jun，Yu Ming，et al.Path planning of automatic parallel parking based on RBF neural network［J］.Journal of Hefei University of Technology:Natural Science Edition，2012，35(4):459-463.

［6］Fraichard T，Scheuer A.From reeds and shepp’s to continuous-curvature paths ［J］.IEEE Transactions on Robotics，2004，20(6):1025-1035.

［7］Wang Y J，Cartmell M P.Autonomous vehicle parallel parking design using function fitting approaches［J］.Robotica，16(2):159-170.

［8］Gómez-Bravo F，Cuesta F，Ollero A，et al.Continuous curvature path generation based on β-spline curves for parking manoeuvres ［J］.Robotics and Autonomous Systems，2008，56(4):360-372.

［9］Zhao Y N，Emmanuel G，Collins Jr.Robust automatic parallel parking in tight spaces via fuzzy logic［J］.Robotics and Autonomous Systems，2005，51(2/3):111-127.

［10］Ollero A，García-Cerezo A，Martínez J L，et al.Fuzzy tracking methods for mobile robots［M］∥Jamshidi M，ed.Applications of fuzzy logic:towards high machine intelligence quotient systems.Upper Saddle River:Prentice-Hall，1997:347-364.

［11］Demirli K，Khoshnejad M.Autonomous parallel parking of a car-like mobile robot by a neuro fuzzy sensor based controller［J］.Fuzzy Sets and Systems，2009，160(19):2876-2891.

［12］Lian K Y，Chiu C S，Chiang T S.Parallel parking a carlike robot using fuzzy gain scheduling ［C］∥Proceedings of 1999 IEEE International Conference on Control Applications.Hawai:IEEE，1999:1686-1691.

［13］Gao Z Q.Scaling and bandwidth-parameterization based controller tuning ［C］∥Proceedings of the American Control Conference.Denver:IEEE，2003:4989-4996.

［14］韩京清.从PID 技术到自抗扰控制技术［J］.控制工程，2002，9(3):13-18.Han Jing-qing.From PID technique to active disturbances rejection control technique［J］.Control Engineering of China，2002，9(3):13-18.

［15］陈增强，孙明玮，杨瑞光.线性自抗扰控制器的稳定性研究［J］.自动化学报，2013，39(5):574-580.Chen Zeng-qiang，Sun Ming-wei，Yang Rui-guang.Research on the stability of linear active disturbance rejection control［J］.Acta Automatica Sinica，2013，39(5):574-580.

［16］杨志强，谭彧.车道保持系统的车辆状态预测模型［J］.农业机械学报，2008，39(10):25-29.Yang Zhi-qiang，Tan Yu.Model based on states preview for lane keeping system［J］.Transactions of the Chinese Society for Agricultural Machinery，2008，39(10):25-29.