新型空间5 自由度并联机构的奇异位形分析与规避*

陈炳发 丁旺生 丁力平 陈文亮

( 南京航空航天大学 机电学院，江苏 南京 210016)

并联机构具有高刚度、高精度和高承载力等特点，因此在机器人领域得到了广泛应用.其中，5 自由度并联机构是少自由度并联机构中极为重要的一类，有着突出的应用前景［1］.在机构设计方面，王海东等［2］提出了4PSS +PRPaU 5 自由度新型并联机床的概念设计，Yi 等［3］提出了一种3 支链5 自由度2SPS + UPU 并联机构，Chen 等［4］提出了一种4UPS+RPS 5 自由度并联机构.上述机构的共同特点是能实现动平台的三维转动和两维移动共5 个自由度.但迄今为止，能实现三维移动和两维转动自由度的并联机构则相对较少.

当机构出现奇异位形时，其自由度会发生变化，使机构失去控制，甚至对机构造成破坏［5-6］.因此，奇异位形分析与规避是并联机构设计中的重要研究内容.目前，并联机构奇异性的研究方法主要有基于机构输入、输出速度的分析方法，Grassmann线几何法，基于矩阵的分析方法以及基于螺旋理论的分类方法等［7］.很多学者对并联机构奇异位形的规避也做了研究.Yiu 等［8］提出利用冗余驱动来消除奇异，然而该方法只能消除机构的驱动奇异，对运动奇异通常没有效果，同时可能会产生新的奇异位形; Sen 等［9］提出利用规划路径的方法来规避奇异位形，但是对于具有连续工作空间和轨迹控制要求的并联机构，通过轨迹规划规避运动奇异性是不可行的［10］，因此这类规避方法在实际应用中具有一定的局限性.文中采用约束支链法设计了一种新型的、能够实现动平台三维移动和两维转动的5 自由度并联机构，利用雅克比矩阵推导出了机构产生奇异位形的判断条件，并根据此判断条件给出了两种规避机构奇异位形的方法.

1 2UPS+PRRPR 并联机构的描述

所设计的2UPS+PRRPR 5 自由度并联机构模型如图1 所示，机构的坐标示意图见图2.该机构包括定平台、动平台，以及固定在定平台上的直线导轨和支链1、2、3.其中，支链1 和3 是2 条相同的UPS 支链，支链2 为PRRPR 支链，是含一移动输入和一转动输入的约束链( U、P、S、R 分别表示虎克铰、移动副、球铰、转动副) .杆L2中的移动副和转动 副1 为 支 链2 中 的 驱 动 副1、2.支 链3 中 的 移 动副为驱动副3，支链1 中的移动副和虎克铰第二转动副为驱动副4、5.其中，支链1、3 中虎克铰的第一转动副以及支链2 中的转动副1、2 均与X 轴平行.虎克铰的第二转动副和支链2 中的转动副3 均与Y轴平行.支链1、3 中与动平台相连的S 副中心分别记为A1、A3，与定平台连接的U 铰中心分别记为B1、B3.支链2 与定平台相连的滑块副中心记为B2，与动平台连接的转动副中心记为A2.该并联机构含有串联输入支链，故通过3 条支链可实现动平台三维移动和两维转动共5 个自由度的运动要求，结构相对简单，姿态调解能力强，可实现部分控制解耦.

图1 2UPS+PRRPR 并联机构模型Fig.1 Model of 2UPS+PRRPR parallel mechanism

图2 并联机构坐标示意图Fig.2 Coordinate diagram of parallel mechanism

2 自由度分析

支链2 的螺旋系图如图3 所示.为方便起见，确定X 轴为沿转动副1 的轴线方向，Z 轴竖直向上，Y轴由右手定则确定.在动平台运动过程中，PRRPR支链的5 个螺旋的表达式如下:

式中，ai、bi( i=1，2，3) 为运动副轴线在O-XYZ 坐标系中的坐标.

图3 约束支链螺旋示意图Fig.3 Schematic diagram of the spiral of constrained branchedchain

对式( 1) 描述的分支螺旋系求反螺旋，得出PRRPR 分支的约束力螺旋为

式(2) 表示垂直于动平台的一个约束力偶，它限制动平台沿自身法线方向的转动.

采用修正的G-K［11］公式计算机构自由度M:

式中:d 为机构的约束数，d=6－ ，为公共约束数;n 为机构的构件数; g 为机构运动副总数; fi为第i个运动副的自由度数; v 为冗余约束数; ξ 为机构存在的局部自由度数.

由于支链1、3 的自由度为6，属于非约束支链，这样3 条支链对动平台共同提供一个沿动平台法线方向的约束力偶;并且，该机构没有公共约束，因此=0，同时也无冗余约束，因此v=0.将上述数值代入式(3) ，可得M=5.由此证明所设计的并联机构具有三维移动和两维转动共5 个自由度.

3 雅克比矩阵推导

3.1 约束子矩阵

动平台的瞬时速度用$p=() 表示，其中ωA表示动平台相对于定坐标系的转动速率，vA表示动平台相对于定坐标系的移动速率.$p可以表示为支链上各个运动的线性组合［12-13］:

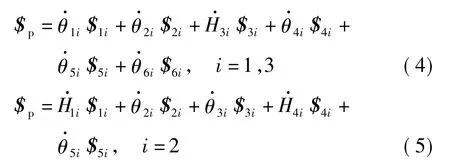
由图4 可知，支链1、3 中各关节的运动螺旋可表示为

其中i=1，3.

同理，支链2 中各关节的运动螺旋为$12=

图4 2UPS+PRRPR 并联机构螺旋图Fig.4 Spiral diagram of 2UPS+PRRPR parallel mechanism

两个共面的线矢量互为反螺旋，轴线相互垂直的偶量与线矢量互为反螺旋，因此可通过几何方法得到支链2 上的反螺旋.较简单的方法是找到一个偶量，单位向量

式(6) 可以写成矩阵形式:

式中，

Jc称为约束子矩阵，其行矢量的物理意义就是由支链2 加在动平台上的约束螺旋.由于支链1、3 对动平台没有提供约束，因此约束子矩阵不包括这两条支链中的关节信息.

3.2 运动子矩阵

当锁定支链1、3 中的驱动副3 和4 时，增加的反螺旋与其他5 个螺旋的互易积应该为零，并且与$3i的互易积不为零.由于两个共面的线矢量互为反螺旋，故容易找到经过Ai、Bi的线矢量与5 个螺旋分别共面.该反螺旋为

同理，当锁定支链1 虎克铰上的转动驱动$21时，增加的反螺旋为，此螺旋为经过A1点且与$11平行的线矢量，

支链2 中，当锁定转动副$22时，增加的驱动力反螺旋与$11、$32、$42、$52的互易积为0，须过D点与$12和$42相垂直.因此，

同理，锁定移动副$42时，增加的驱动力反螺旋是过点D、B2的线矢量:

上式写成矩阵形式为

式中，

将式(10)－(12) 写成矩阵形式:

联合Ja1、Ja2得到机构的运动子矩阵:

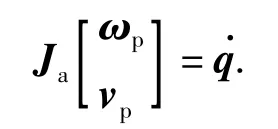
式中，ωp和vp分别表示动平台的角速度和线速度，

Ja是该机构的运动子矩阵，其行矢量表示的是各支链对动平台的驱动力.

联合式(8) 、(13) 可得

式中，

J 是一个6 ×6 矩阵，是该机构的完整雅克比矩阵，包含了该机构的约束和运动特性.根据式(15) ，可以分析得出此机构的全部奇异类型条件.

4 奇异位形分析

当完整雅克比矩阵J 为不满秩矩阵时，机构将产生奇异位形，包括约束奇异和运动奇异［14］.当J的子矩阵Jc为非满秩时，机构存在约束奇异; 当子矩阵Ja为非满秩时，则机构出现运动奇异.

文中所提机构中，若Jc矩阵秩小于1，机构出现约束奇异.由式(8) 知，此时S52与S32平行.根据机构的结构特点，S52与S32不可能出现平行，因此该机构不存在约束奇异.

图5 ⊥时的奇异位形图Fig.5 Singularity configuration when ⊥

当运动子矩阵Ja为非满秩，或者是完整雅克比矩阵J 为非满秩且约束子矩阵Jc为满秩时，机构出现运动奇异.通过式(13) 、(15) 可知，机构在下列情况下发生运动奇异:和线性相关或和线性相关，但满秩.例如，当支链2 运动到AD⊥DB2时，与共轴并线性相关，此时Ja的秩降为4，机构出现运动奇异.由2UPS + PRRPR 并联机构的特点可知，当⊥时，动平台在Z 轴正向或Y 轴负向的位移达到边界，即奇异位形属于边界奇异，如图5 所示.

通过上述分析可知，2UPS + PRRPR 机构不存在约束奇异，运动奇异仅出现在L2与L 相垂直时，奇异位形相对较少.

5 奇异位形的规避

图6 2UPS+PRRPR 并联机构的奇异位形Fig.6 Singularity configuration of 2UPS + PRRPR parallel mechanism

根据奇异位形产生的条件，可得到机构出现奇异位形时的判别条件:

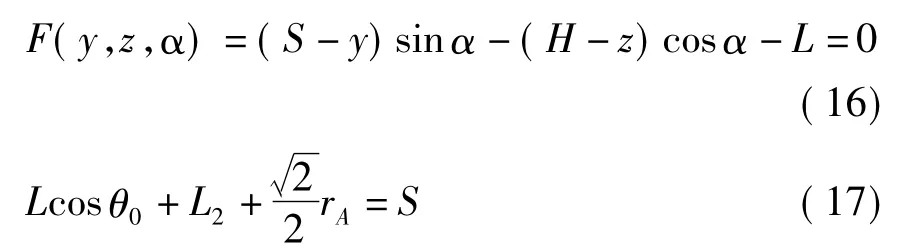
式中，rA为机构动平台外接圆半径.

当姿态角不变时，2UPS + PRRPR 并联机构的奇异位形与动平台在z 向的最大和y 向的最小运动范围有极大关系.给定α、y 时，由式( 16) 可解得出现奇异位形时的zmax值:

zmax=sec α( Hcosα－Ssin α+ysin α+L) .

约束动平台在z 正向的运动范围小于zmax即可规避奇异位形的出现.

同理，给定α、z，由式(16) 可解得机构出现奇异位形时的ymin值:

ymin=csc α［( z－H) cosα+Ssin α－L］.

约束动平台在y 向运动的最小值大于ymin即可规避奇异位形.当动平台在y 向运动的最小值需要减小时，可以通过减小其在z 向运动的最大值，而当动平台在z 向运动的最大值需要增大时，可以通过增大其在y 向运动的最小值，以实现对工作空间内奇异位形的规避.

给定z、y 值时，由式(16) 可解得出现奇异位形时的αmax值:

通过约束动平台绕X 轴的最大转角αmax，亦可避免奇异位形的出现.

2UPS+PRRPR 并联机构的奇异位形规避也可通过优化结构参数来实现.杆L2与定长杆L 垂直( 即AD 与以B2D 为半径的圆相切) 时机构出现奇异位形，如图7 所示.当给定动平台的工作空间范围，即给定αmax、ymin、zmax时，机构的奇异位形见图7.

图7 奇异位形规避示意图Fig.7 Schematic diagram of singularity configuration avoidance

由式(16) 、( 17) 可解出定长杆L，改变结构参数L 至L'( L'＞L) ，如图7 所示，此时AD'与B2D'不再垂直.由式(16) 可知，αmax、zmax是L 的增函数，ymin是L 的减函数，则动平台在给定的工作空间内将无奇异位形出现.

6 数值算例

利用三维边界搜索法［17］分析该机构的工作空间.给定姿态角α、β，通过判断空间一点是否为工作空间的边界点，最后得到所有点的集合，即为工作空间的边界.图9 为定姿态角rad、β=0 rad 时机构的工作空间.

图8 机构的奇异轨迹曲面Fig.8 Singular trajectory surface of the mechanism

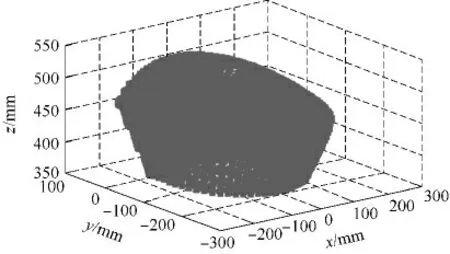
图9 定姿态工作空间Fig.9 Work space under fixed posture

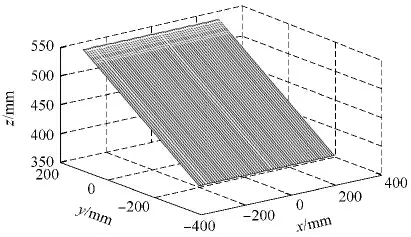
图10 定姿态位置奇异曲面Fig.10 Singularity configuration surface in fixed posture position

定姿态工作空间所包络的定姿态位置奇异曲面部分即为该机构在工作空间内的奇异位置，如图11 所示.

针对以上工作空间内机构出现的奇异位形，利用第5 节中给出的两种奇异位形的规避方法，可避免机构在此定姿态工作空间内出现奇异位形.具体如下:

(1) 选择动平台工作范围.利用奇异位形判别条件对机构奇异性进行分析.若式( 16) 成立，则在此点机构奇异;若不成立，则此点无奇异.给定α=rad、y=－40mm时，由第5 节可知zmax=453.2mm，此时⊥，机构奇异.限制动平台在z 向的运动范围小于zmax，则不会出现奇异位形，如图12 所示，约束范围内判别条件式F( y，z，α) ≠0.同理可验证，适当约束动平台运动参数αmax、ymin的范围，可避免奇异位形出现.

图11 定姿态工作空间内的位置奇异曲面Fig.11 Position singularity configuration surface in the work space under fixed posture

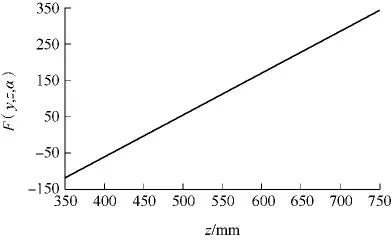
图12 奇异点与z 向位移的关系Fig.12 Relationship between singular point and z displacement

图13 改进前后奇异点相对z 向的位置Fig.13 Location of singular point relative to z displacement before and after the improvement

(2) 改变结构尺寸.当αmax、ymin、zmax分别给定为rad、550 mm、－40 mm 时，由第5 节可知出现奇异位形的定长杆L 为750 mm，将结构参数L 改为800 mm，利用式( 16) 奇异位形判别条件，可知改进后的边界奇异点出现在所要求的工作区间外，如图13 所示.改进后，机构在给定工作空间范围内无奇异位形出现.

7 结语

文中采用约束支链法设计了一种新型5 自由度并联机构，其结构相对简单，奇异位形相对较少，该机构在工业机器人、微动机器人、虚拟轴并联机床等领域具有广泛的应用前景.

文中还通过螺旋理论推导得到了该并联机构的完整雅克比矩阵，包括约束子矩阵和运动子矩阵.根据雅克比矩阵的秩分析了该并联机构产生约束奇异和运动奇异的所有条件.研究表明，通过选择动平台工作范围或改变结构尺寸，可以避免机构出现奇异位形.文中研究为后续机构的运动轨迹规划提供了理论依据，并为相似并联机构规避奇异位形提供了方法参考.

［1］Stewart D.A platform with six degrees of freedom［J］.Proc Inst Mech Eng，1965，180(15) :371-378.

［2］王海东，韩玉，杨炳恒.一种新型五自由度并联机床的概念设计与运动分析［J］.机械传动，2011，35(8) :68-71.Wang Hai-dong，Han Yu，Yang Bing-heng.Configuration design and kinematics analysis of a new 5-DOF parallel machine tool［J］.Mechanical Transmission，2011，35(8):68-71.

［3］Yi Lu，Zhang Xuili，Sui Chunping，et al.Kinematics/statics and workspace analysis of a 3-leg 5-DoF parallel manipulator with a UPU-type composite active constrained leg［J］.Robotica，2013，31(2) :183-191.

［4］Chen Xiulong，Sun Xianyang.Dexterity analysis of 4-UPSRPS parallel mechanism［J］.International Journal of Advanced Robotic Systems，2012，9(144) :1-8.

［5］高征，高峰.新型并联机器人的奇异位形分析［J］.机械工程学报，2008，44(1) :133-138.Gao Zheng，Gao Feng.Singularity loci analysis of a new parallel manipulator［J］.Chinese Journal of Mechanical Engineering，2008，44(1) :133-138.

［6］Gosselin C，Angeles J.Singularity analysis of closed-up kinematics chains ［J］.IEEE Transactions on Robotics and Automation，1990，6(3) :281-290.

［7］彭铁柱，李凌丰.无奇异3UPS +1RPU 新型并联机构［J］.浙江大学学报:工学版，2011，44(11) :2056-2062.Peng Tie-zhu，Li Ling-feng.Analysis of a novel 3UPS +1RPU parallel mechanism without singularity［J］.Journal of Zhejiang University:Engineering Science，2011，44(11):2056-2062.

［8］Yiu Y K，Cheng H，Xiong Z H，etal.On the dynamics of parallel manipulators［C］∥Proceedings of MIEEE International Conference on Robotics ＆Automation.Seoul:IEEE，2001:146-154.

［9］Sen S，Dasgupta B，M Allik A.Variational approach for singularity-free path-planning of parallel manipulators［J］.Mechanism and Machine Theory，2003，38( 10) :1165-1183.

［10］王玉新，李雨桐，郭瑞琴.并联机构以保持构型通过奇异位形的方法［J］.机械工程学报，2008，44(6):125-130.Wang Yu-xin，Li Yu-tong，Guo Rui-qin.Method for parallel manipulators to pass through singular points with its original configuration ［J］.Chinese Journal of Mechanical Engineering，2008，44(6) :125-130.

［11］黄真，刘婧芳，李艳文.论机构自由度:寻找了150年的自由度通用公式［M］.北京:科学出版社，2011.

［12］李永刚，宋轶民，冯志友，等.4 自由度非对称并联机构的完整雅克比矩阵［J］.机械工程学报，2007，43(6) :37-40.Li Yong-gang，Song Yi-min，Feng Zhi-you，et al.Complete Jacobian matrix of a class of incompletely symmetrical parallel mechanisms with 4-DOF［J］.Chinese Journal of Mechanical Engineering，2007，43(6) :37-40.

［13］张彦斌，刘宏昭，吴鑫.基于互易螺旋理论的无奇异完全各向同性移动并联机构型综合［J］.机械工程学报，2008，44(10) :83-88.Zhang Yan-bin，Liu Hong-zhao，Wu Xin.Type synthesis of non-singular fully-isotropic translational parallel mechanisms based on theory of reciprocal screw ［J］.Chinese Journal of Mechanical Engineering，2008，44(10) :83-88.

［14］Joshi S A，Tsai L W.Jacobian analysis of limited-DOF parallel manipulators［J］.ASME Journal of Mechanical Design，2002，124(2) :254-258.

［15］程世利，吴洪涛，王超群，等.平面平台型Stewart 并联机构的奇异性分析［J］.机械工程学报，2011，47(9):1-7.Chen Shi-li，Wu Hong-tao，Wang Chao-qun，et al.Sigularity analysis of Stewart parallel mechanism with planar platform［J］.Journal of Mechanical Engineering，2011，47(9) :1-7.

［16］张耀军，张玉茹.基于Grassmann 线几何的平面柔索驱动并联机构奇异分析［J］.机械工程学报，2011，47(10) :1-7.Zhang Yao-jun，Zhang Yu-ru.Singularity analysis of planar cable-driven parallel mechanisms with Grassmann geometry［J］.Journal of Mechanical Engineering，2011，47(10) :1-7.

［17］曹永刚，张玉茹，马运忠.6-RSS 型并联机构的工作空间分析与参数优化［J］.机械工程学报，2008，44(1) :19-24.Cao Yong-gang，Zhang Yu-ru，Ma Yun-zhong.Workspace analysis and parameter optimization of 6-RSS parallel mechanism［J］.Chinese Journal of Mechanical Engineering，2008，44(1) :19-24.