基于鲁棒观测器的电液伺服系统传感器故障检测与隔离*

徐巧宁 喻峰 周华† 杨华勇

(1.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027;2.中国船舶重工集团第七〇七研究所 九江分部，江西 九江 332007)

对电液伺服系统进行状态监测与故障检测时，往往会引入额外的传感器.由于这些传感器位于系统的反馈通道上，因此不能像前向通道中的元件那样依靠反馈机制对参数摄动和干扰进行调节，一旦这些传感器出现故障，就会影响对原来系统的故障判断.目前的许多研究只考虑了系统的故障检测而忽略了对这些传感器故障的检测与隔离.

电液伺服系统是一个典型的非线性系统，且在运行过程中会受到一些未知和时变的干扰力［1］，这给传感器故障的检测与隔离带来了困难.文献［2-3］和文献［4］中分别通过构建神经网络和搭建主成分模型来进行传感器故障的检测与隔离，这两种方法均需利用大量典型的历史数据，且网络的构造及主成分模型的建立并不容易.文献［5］中采用卡尔曼滤波的方法对电液伺服系统的传感器故障进行检测，检测过程中对系统进行了线性化，线性化的系统只能代表局部的运行区域，对于其他区域则会产生较大的偏差.文献［6-9］中从多个方面对非线性系统的传感器故障检测进行了研究，但所提出的模型中没有考虑干扰的影响.文献［10］中所设计的鲁棒观测器需要在系统满足一定几何条件的情况下才能对干扰进行解耦.文献［11-12］中事先对非线性系统中的未知干扰进行测算，再进行观测器的设计，然而干扰在实际系统中是难以准确测得的.此外，在电液伺服系统的相关研究中，也很少涉及对传感器故障的隔离［4，9，11］，系统的非线性以及未知干扰更是给故障隔离带来了困难.

有鉴于此，文中提出了一个基于非线性鲁棒观测器的方案来对电液伺服系统的传感器故障进行检测与隔离.非线性鲁棒观测器可以对电液伺服系统的非线性及未知干扰进行处理.另外，为了辨识各个传感器的故障，采用了鲁棒观测器组结合逻辑判断的方式.文中分别通过仿真和实验对所提方案进行了验证，并根据实际需要设计了自适应阈值进行故障决策.仿真和实验结果均验证了所提方案的有效性.

1 系统分析

1.1 系统简介

所研究的电液伺服系统如图1 所示.这是一个典型的阀控单出杆缸位置控制系统，由比例阀控制进出液压缸的油液，进而控制活塞的运动;活塞的位移通过齿轮齿条装置装换为角度信号，通过与指令角度相比较，控制器给出一个信号，最终控制活塞达到所需位置;液压锁用来保持活塞位置不变.为了对系统进行状态监测，在液压缸的进出口处分别设置了两个压力传感器，通过对状态量的监测可以检测出系统内部的许多故障［13-15］.

图1 电液伺服系统原理图Fig.1 Schematic diagram of electro-hydraulic servo system

1.2 数学建模

比例阀的流量方程如下:

式中，xv和W 分别为比例阀的阀芯位移与死区，q1和q2分别为进出液压缸无杆腔和有杆腔的流量，kq为流量系数，ps和pr分别为供油和回油压力，p1和p2分别为油缸无杆腔和有杆腔的压力.

比例阀的动态方程用一个一阶模型表示为

式中，kv与 分别为描述比例阀动态特性的增益与时间系数，u 为输入电压.

液压缸的流量连续性方程为

式中，xp为活塞的位移，A1和A2分别为液压缸无杆腔、有杆腔的有效面积，V1和V2分别为液压缸无杆腔、有杆腔的容积，Ci和Ce分别为液压缸的内、外泄露系数，βe为有效体积弹性模量.

液压缸和负载力的平衡方程为

式中:m 为折算到负载的总质量;d 为作用在活塞上的未知力，d=bpp+Fext，bp为粘性阻尼系数，Fext为其他外负载力(包括摩擦力和干扰力等).

定义系统状态变量为x=［˙xpp1p2xv］T，输入为u.根据式(1)-(4)，可以得到系统的状态方程为

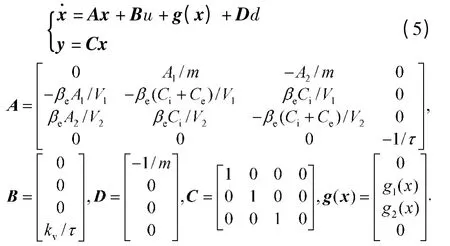
若xv＞W，则

若xv＜-W，则

根据式(1)-(4)，可得到如图2 所示的电液伺服系统方框图，其中Gc(s)是控制器模块，其余传递函数表示为

图2 电液伺服系统方框图Fig.2 Block diagram of electro-hydraulic servo system

基于模型的方法不可避免地存在建模误差，对于未知力d，下文介绍的鲁棒观测器会加以处理，其他的建模误差存在于一些难以准确测得的模型参数中，在文中系统内主要为βe、V1、V2与.由图2 可知，这些参数存在于传递函数Gv(s)、G1(s)和G2(s)的时间系数中，它们仅影响系统的瞬态，因此，即使这些参数不完全准确，也不会太大地影响故障检测与隔离的结果.

2 故障检测与隔离

故障检测的目标为:所设计的观测器不受未知干扰的影响而只受故障的影响;故障隔离的目标为:观测器能对哪个传感器发生了故障进行判断.文中所考虑的故障为同一时间仅发生一种故障，多故障的检测与隔离将在以后的工作中加以研究.

带有传感器故障的非线性电液伺服系统可建模为

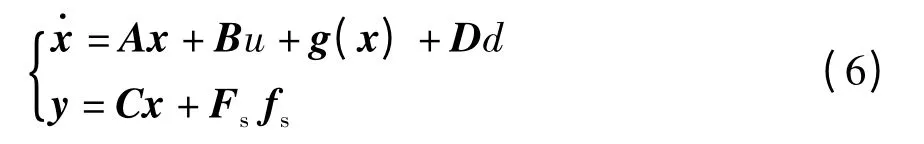
式中，Fs与fs分别表示传感器故障分布矩阵与故障向量.因为系统的状态量是在一定范围内变化的，因此非线性项g(x)可认为是局部Lipschitz 的［16］，存在一个正常数γ，使得下式得到满足:

为了辨识不同的传感器故障，式(6)可写为

式中:yj为y 的第j 个输出量，其余输出量组成yj;Cj与Fsj分别为矩阵C 与Fs的第j 行，C 与Fs中剩下的行组成矩阵Cj与.

设计非线性鲁棒观测器如下:

式中，Nj、Gj、Lj、Tj、Ej为需要设计的未知矩阵，z 为求得的中间过渡向量.

定义状态观测误差e 为

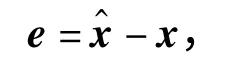
则

式中，Tj=I+EjCj，I 为单位矩阵.

由于传感器故障经常表现为缓变型故障，因此该故障的一阶导数项近似为零，由上可知，要使式(9)为系统的故障检测与隔离观测器，必须满足为列满秩.为了设计方便，可以先设计没有故障时的观测器，然后再把设计得到的系统参数进行检验，满足(NjEj+Lj)Fjs为列满秩这个条件即可.由上可知，Nj=TjA -KjCj，Kj=Lj+NjEj，如果rank(CjD)=rank(D)，则可得

式中，Yj为适当维数的任意矩阵，Uj= -D(CjD)+，Vj=I-(CjD)(CjD)+，(CjD)+为CjD 的广义逆.

定义Lyapunov 函数V=eTPje，其中Pj(Pj＞0)为正定对称矩阵，可得

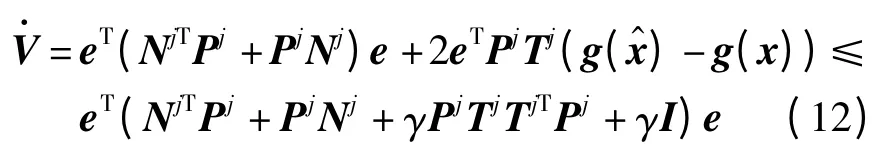
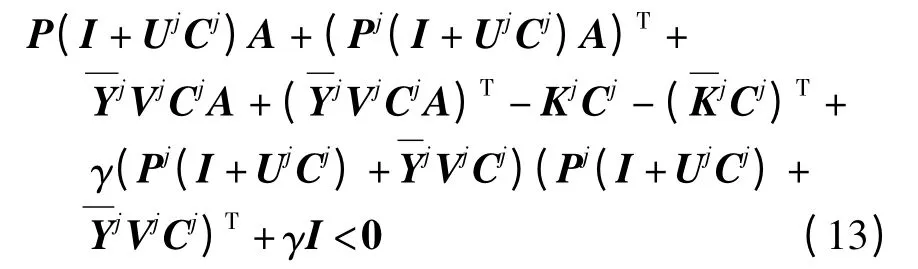
根据Schur 补引理，不等式(13)可以重整为

式中，P1=Pj(I+UjCj)，Y1=YjVjCj，K1=KjCj.

式(14)是一类线性矩阵不等式(LMI)，借助于Matlab LMI 工具箱，可获得和Pj，然后得到观测器的其他参数矩阵.

3 仿真与实验研究

设计3 个观测器——观测器1 用来检测系统有无故障，因此需要对所有的传感器故障都敏感;观测器2 和3 用来对故障进行定位，因此分别对某一传感器故障不敏感.所有观测器均对干扰鲁棒.需要注意的是，由于约束条件rank(CjD)=rank(D)的存在，不能设计出仅角度传感器不敏感的观测器，但由于系统中仅有3 个传感器，可以通过观测器2 和3 组合判断出所有传感器故障.根据第2 节中的观测器设计算法可知，所设计出的3 个观测器均包含速度输出，因此将速度残差(实际测量到的活塞速度与通过观测器计算得到的速度的差值)作为系统故障检测和隔离的依据.

3.1 仿真研究

所提出的故障检测与隔离方案在Matlab 中进行验证.系统参数设置如表1 所示，输入的角度信号为θ～=15°(0 s≤t ＜20 s)，-15°(20 s≤t ＜40 s)，0°(40 s≤t ＜60 s)，其中t 表示时间.

表1 系统参数及取值Table 1 System parameters and their values

正常情况下，仿真得到的活塞速度以及通过观测器得到的速度分别如图3(a)中实线与虚线所示，将它们相减得到速度残差，如图3(b)所示，可见两个速度基本重合，残差大约为零，说明设计的观测器具有较好的观测能力.

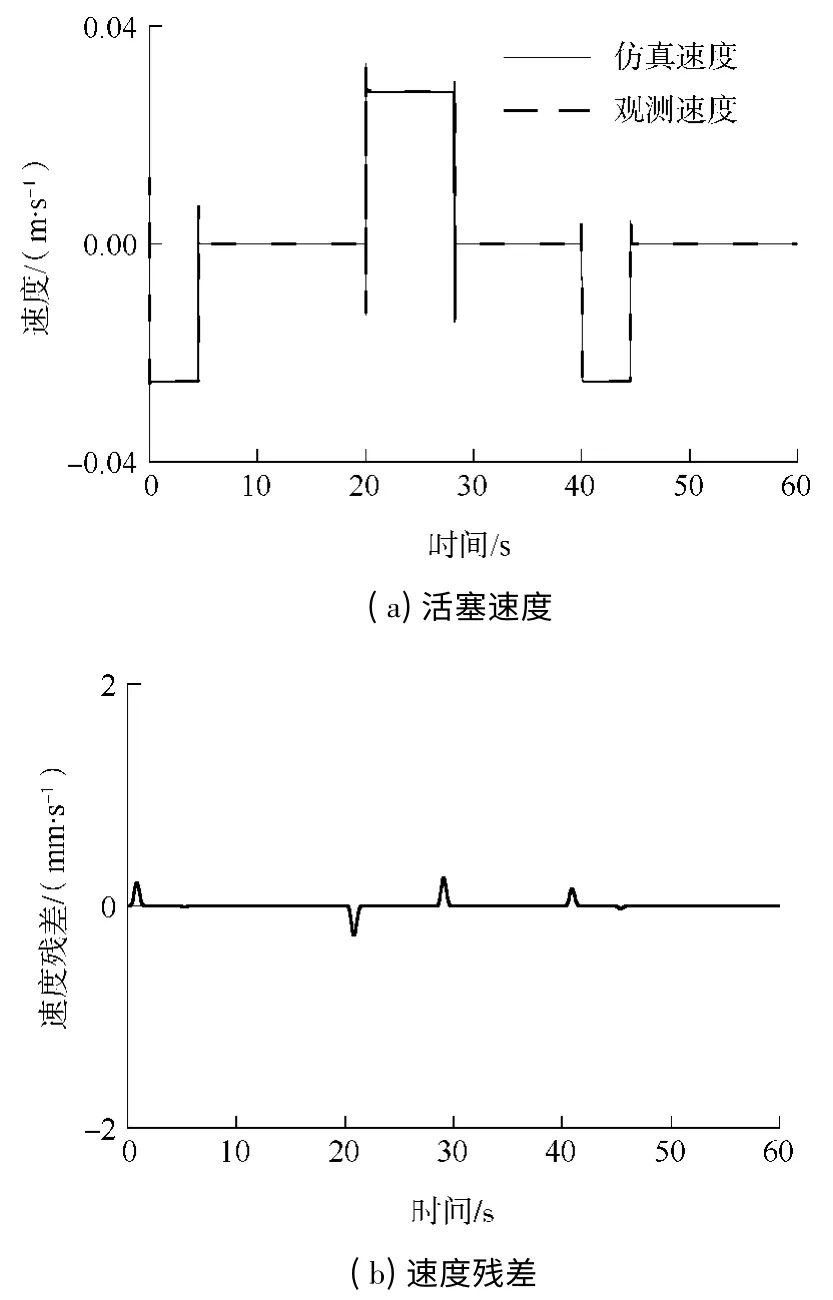
图3 活塞速度及其残差的仿真结果Fig.3 Simulated velocities and their residuals of piston

为了检测观测器对未知干扰力的鲁棒性，设计两组仿真实验.组A 中加上了实时波动的干扰力Fext，Fext=2sin(8t)+1.2sin(5t)(单位:kN)，检测结果如图4(a)所示，组B 中加上了随活塞位置(即角度)变化的干扰力Fext=0.7θ(单位:kN/(°))，检测结果如图4(b)所示，可见两组速度残差都约为零，说明所设计的观测器对干扰力具有较好的鲁棒性.

将压力传感器P1、P2 的输出分别加上0.3 和0.6 MPa，角度传感器An 的增益乘以0.87 和0.73，模拟3 个传感器两种不同程度的故障——故障1 与故障2.故障检测与隔离的仿真结果如图5 所示.由图5 可见，观测器2 仅对P1 故障不敏感，观测器3仅对P2 故障不敏感，其他情况下的速度残差在两个运动方向上(v-与v+)均发生了偏离，且故障程度越大残差偏离得越多.

上述结果验证了3 个鲁棒观测器的作用——观测器1 对所有传感器故障均敏感，可以作为系统有无故障的初始判断;P1 发生故障时，观测器2 残差不偏离;P2发生故障时，观测器3残差不偏离;当3 个观测器均发生偏离时，An 发生故障，通过3 个观测器的配合，可以判断出系统传感器故障的类别.

图4 干扰力及其残差的仿真结果Fig.4 Simulated disturbances and their residuals

模拟传感器突发故障的情况，在25 s 时分别将P 1、P2的输出加上0.6MPa，An的输出乘以0.73，进行3 组仿真.故障检测与隔离结果如图6 所示，可见所有故障均可在故障发生后的0.5 s 内被诊断出来.

图5 传感器故障检测与隔离的仿真结果Fig.5 Simulated results of fault detection and isolation for sensors

3.2 实验研究

搭建的实验台如图7 所示，将4000kg 的质量块加在油缸的活塞杆上来模拟负载，数据采集和诊断算法通过NI-PXI 设备(包括采集卡PXI-6229、控制器PXIe-8108 及机箱等)来实现，采样率为1000 Hz，系统采用了实时模块来提高计算速率和可靠性，程序计算周期为1 ms.

输入及实际角度如图8 所示，实际系统中指令角度的输入是手动操作的，所以每次实验并不能保证角度切换点的时间完全一致，但不会对故障检测结果造成影响.将实际角度乘以比例系数7.6 mm/(°)可得活塞位移，对位移求微分可得速度.

图6 传感器突发故障检测与隔离的仿真结果Fig.6 Simulated results of fault detection and isolation for sudden sensor faults

正常状态下通过3 个观测器得到的速度残差如图9(a)实线所示，实验环境不如仿真环境理想，设计自适应阈值如下:

图7 电液伺服系统实验台Fig.7 Experimental test rig for electro-hydraulic system

图8 输入与实际角度Fig.8 Input and actual angles

对角度传感器An的增益乘以0.73，两个压力传感器P1、P2 的输出分别加上0.6 MPa 来模拟故障.3 个传感器的故障检测与隔离实验结果分别如图9(b)-9(d)所示.3 张图中，观测器1 产生的速度残差在两个方向上均超过阈值，观测器2 产生的速度残差仅在P1 发生故障时未超过阈值，而观测器3产生的速度残差仅在P2 发生故障时未超过阈值，实验结果与仿真结果一致，说明设计的故障检测与隔离方案有效.

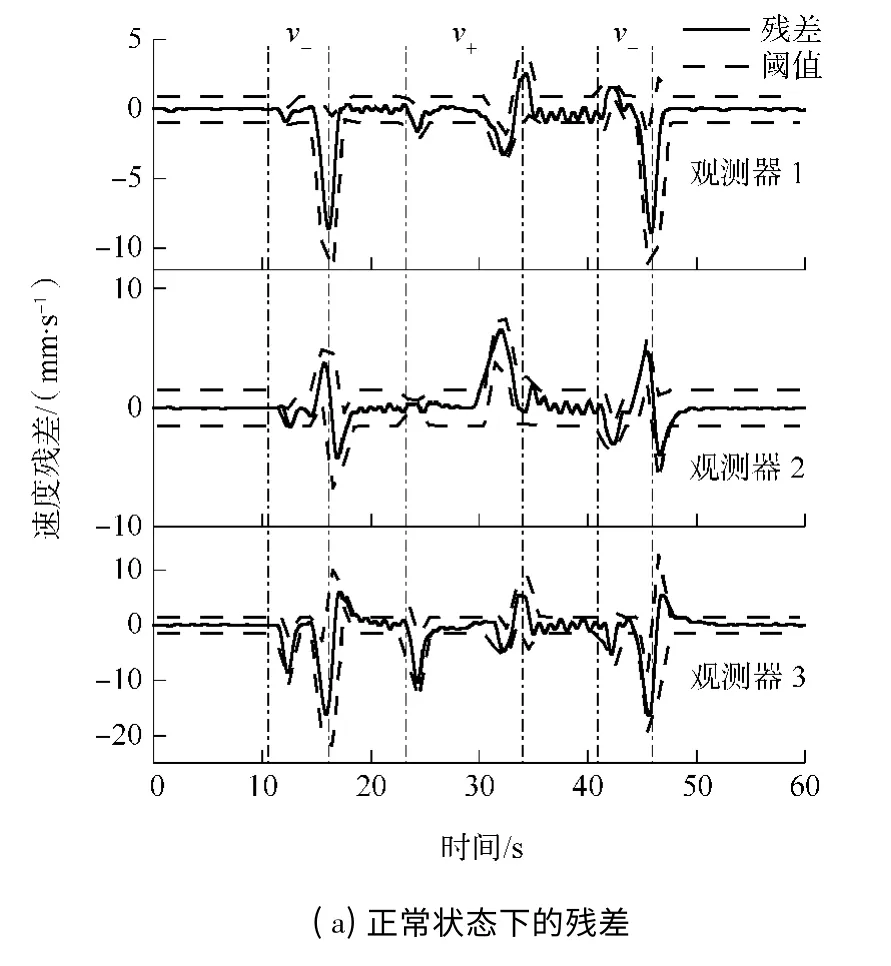
图9 传感器故障检测与隔离的实验结果Fig.9 Experimentalresultsoffaultdetectionandisolationforsensors

图10 传感器突发故障检测与隔离的实验结果Fig.10 Experimental detection and isolation results for sudden sensor faults

模拟传感器突发故障的情形，在活塞速度为正时模拟故障，由于每次实验不能保证故障模拟时刻tf完全一致，因此横坐标以tf为基准进行统一描述，在tf时刻分别将P1、P2 的输出加上0.6 MPa，An 的输出乘以0.73，进行3 组实验.故障检测与隔离结果如图10 所示，可见所有故障均可在故障发生后的1s 内被诊断出来，与仿真结果相比所需时间略长，原因是实际系统毕竟与仿真模型有偏差，实际阈值的设置要略大于仿真阈值，因此检测的时间也略长.

4 结语

针对电液伺服系统的非线性及摩擦力、干扰力未知的情况，文中提出了一种基于鲁棒观测器的电液伺服系统传感器故障检测与隔离方案，以不受上述因素的影响来对系统传感器故障进行诊断.针对观测器设计过程中难以获得有效解的问题，采用线性矩阵不等式进行求解.对于系统中传感器故障的辨识问题，采用观测器组结合逻辑判断的方式来解决.仿真与实验证明:在正常状态下，所设计的鲁棒观测器残差均在阈值范围内;当外干扰力随位置和时间变化时，对残差不会有影响;当任意1 个传感器发生故障时，通过3 个观测器的配合，便可对故障进行检测与隔离.所设计的自适应阈值可以对残差进行有效的故障决策，避免系统误报警.

文中研究的是一类较典型的阀控缸电液伺服系统，在许多场合均有应用.执行器与传感器故障的共同检测与隔离将会是下一步的研究重点.

［1］Mohanty A，Gayaka S，Yao B.An adaptive robust observer for velocity estimation in an electro-hydraulic system［J］.International Journal of Adaptive Control and Signal Processing，2012，26(12):1076-1089.

［2］Wang X，Zhang K.Sensors fault diagnosis of hydraulic automatic gauge control system based on neural network optimized by genetic algorithm［C］∥Proceedings of 2010 International Conference on Electrical and Control Engineering.Wuhan:IEEE，2010:3009-3012.

［3］Talebi H A，Khorasani K，Tafazoli S.A recurrent neuralnetwork-based sensor and actuator fault detection and isolation for nonlinear systems with application to the satellite’s attitude control subsystem［J］.IEEE Transactions on Neural Networks，2009，20(1):45-60.

［4］Tao E P，Shen W H，Liu T L，et al.Fault diagnosis based on PCA for sensors of laboratorial wastewater treatment process［J］.Chemometrics and Intelligent Laboratory Systems，2013，128:49-55.

［5］Kennedy P，Ushakumari S，Jayakumar M.Detection of sensor faults in an electro hydraulic actuator［C］∥ICTT Electrical Engineering Papers.Trivandrum:［s.n.］，2011:1-7.

［6］Yan X G，Edwards C.Sensor fault detection and isolation for nonlinear systems based on a sliding mode observer［J］.International Journal of Adaptive Control and Signal Processing，2007，21(8/9):657-673.

［7］Rajamani R，Ganguli A.Sensor fault diagnosis for a class of nonlinear systems using linear matrix inequalities［J］.International Journal of Control，2004，77(10):920-930.

［8］Pertew A M，Marquez H J，Zhao Q.LMI-based sensor fault diagnosis for nonlinear Lipschitz systems［J］.Automatica，2007，43(8):1464-1469.

［9］Zhang X.Sensor bias fault detection and isolation in a class of nonlinear uncertain systems using adaptive estimation［J］.IEEE Transactions on Automatic Control，2011，56(5):1220-1226.

［10］Jiang B，Staroswiecki M，Cocquempot V.Fault estimation in nonlinear uncertain systems using robust/slidingmode observers ［J］.IEE Proceedings-Control Theory and Applications，2004，151(1):29-37.

［11］Paviglianiti G，Pierri F，Caccavale F，et al.Robust fault detection and isolation for proprioceptive sensors of robot manipulators［J］.Mechatronics，2010，20(1):162-170.

［12］Sepasi M，Sassani F.On-line fault diagnosis of hydraulic systems using unscented Kalman filter［J］.International Journal of Control，Automation，and Systems，2010，8(1):149-156.

［13］明廷涛，张永祥，沈健春，等.阀控非对称缸电液伺服系统的线性鲁棒观测器设计［J］.农业工程学报，2010，26(1):182-187.Ming Ting-tao，Zhang Yong-xiang，Shen Jian-chun，et al.Linear robust observer design for electro-hydraulic valvecontrolled single rod cylinder servo system［J］.Transactions of the CSAE，2010，26(1):182-187.

［14］He X.Fault diagnosis approach of hydraulic system using FARX model［J］.Procedia Engineering，2011，15:949-953.

［15］Dong M，Liu C，Li G.Robust fault diagnosis based on nonlinear model of hydraulic gauge control system on rolling mill［J］.IEEE Transactions on Control Systems Technology，2010，18(2):510-515.

［16］Zemouche A，Boutayeb M.On LMI conditions to design observers for Lipschitz nonlinear systems［J］.Automatica，2013，49(2):585-591.