基于修正的轮胎刷子模型的轮胎纵向力分析*

赵又群 李波 臧利国 张明杰 陈月乔

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

车轮是汽车的重要组成部件，也是汽车与地面接触的唯一媒介，起到支撑负荷，向地面传递制动力、驱动力和转向力，以及缓冲减振的作用.轮胎纵向力学特性是汽车驱动性能和制动性能的关键影响因素［1-2］.轮胎中橡胶的存在，导致车轮具有粘弹性特征，而且车轮通常是边滚边滑.车轮接地区域分为附着区和滑移区.在附着区，轮胎与地面之间没有相对滑动，静摩擦力提供纵向力;在滑移区，轮胎与地面之间存在相对滑动，动摩擦力提供纵向力.因此，在车路接地印迹内，轮胎的受力状况对汽车行驶稳定性和操纵性具有重要影响.

在轮胎建模领域，研究者们进行了大量的探索［3-12］，建立了经验模型和物理模型两大类模型.经验模型根据车轮实验数据，通过插值或函数拟合方法给出预测车轮特性的公式，需要大量的实验数据;物理模型则是根据车轮与路面之间的相互作用机理和力学关系来建立，用以预测力或力矩的变化.在物理模型中，车轮通常被简化为一系列理想化、具有给定物理特性的、径向排列的弹性单元体.研究者们利用各种物理模型对充气轮胎性能进行了分析［13］.文中在充分考虑轮胎与路面接触区域摩擦状况的基础上，建立了考虑胎面和胎肩刚度影响的、修正的轮胎刷子模型，推导了车轮纵向力解析表达式，并通过实验验证了所提模型的有效性.

1 魔术公式概述

Pacejka 等［14-15］提出的魔术公式(Magic Formula)在轮胎仿真领域应用非常广泛，该公式是一个基于纵向力、侧向力和回正力矩测量数据的半经验公式.每种轮胎的特性取决于一套系数，这些系数的数量取决于特定的输出参数，如纵向力、侧向力和回正力矩.通过输入垂向载荷、滑移率和侧倾角度，魔术公式可以用来计算力和力偶.关于纵向力Fx的计算如下所示:

Fx=Dsin(C tan－1(Bφ)).

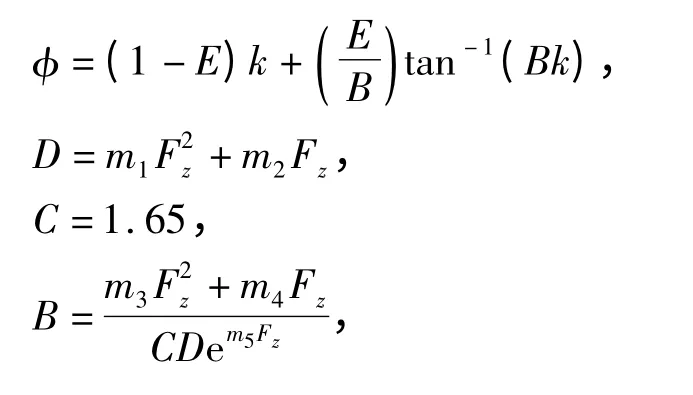
式中:m1，…，m8为轮胎待定系数;k 为滑移率;Fz为垂向载荷.

这种半经验模型需要依靠大量的实验数据，计算量大.

2 刷子模型的建立

如图1 所示，利用刷子模型来对充气轮胎进行简化［16］，把车轮看做由连接在刚性基座(轮缘)上的一系列可以产生伸缩变形的弹性刷毛所组成，这些刷毛起到承受垂向载荷以及产生车轮纵向、侧向力的作用.自由滚动工况下，刷毛的变形如图2(a)所示，刷毛接地区域长为2a，由于路面摩擦力的作用，当车轮滚动速度大于车轮平移速度时，此时刷毛接地端有“粘附于路面”的趋势，从而使刷毛单元产生变形，其两端产生速度差，如图2(b)所示.

图1 车轮及其简化模型Fig.1 Wheel and its simplified model

图2 车轮纵向力的产生机理Fig.2 Formation mechanism of longitudinal force of wheel

刷毛接地长2a，高(即刷毛长度)h，以刷毛单元A-A1为例，其运动形式如图3 所示.相对于车轮中心，刷毛单元A 点以角速度w 向后转动，r 为等效半径，下端A1由于路面附着的作用，以角速度u/r 向后转动.因此，刷毛在x 方向的纵向变形Δx 为

图3 刷子模型纵向受力图Fig.3 Longitudinal force diagram of brush model

首先是真之位置从存在(者)自身转移到了人的行为，具体说来则是转移到了人的理智陈述中。[5]231-232这一位置的转变在《存在与时间》范围内是着眼于此在的展开性和时间性来考察的，在1930年代的思想转向之后则在形而上学的历史发生中被确定。

式中，cex为刷毛单元的纵向刚度.因此，整个接触区域的纵向力可以由积分得出，即

若将纵向力简化为

cx(cx=2cexa2)为弹性梁纵向滑转刚度，由式(4)可以看出，接触区域的刷毛纵向力与滑转率成线性正比关系.考虑弹性梁接地印迹内的垂向载荷分布情况:

cez为弹性梁垂向刚度，若垂向力Fz已知，可由表达式求出cez.若地面附着系数为μ，则每一个单元的最大纵向力有如下关系式:

Fex≤μFez(x).

轮胎接地区域纵向力Fex的分布如图4 所示.可以看出，临界点xs将整个接地区域分为两部分，前为附着区，后为滑移区，滑移区长度为

可以根据如下方程求解xs(通过式(2)和(5)中的x=xs):

Fex=μFez(x).

根据式(2)和(5)，

cexσx(a－x)=μcez(a2－x2)，

因此整个接地印迹的纵向力为两部分之和:

即

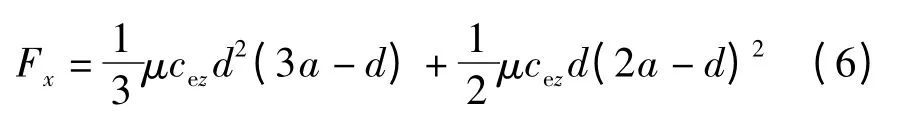
图4 接地区域的驱动力分布情况Fig.4 Driving force distribution on contact patch

3 刷子模型的修正

在式(6)中，车轮与地面之间的摩擦系数(即地面附着系数)为μ，这显然不准确，需要进行修正.由于在实际情况下静摩擦系数μst通常大于滑动摩擦系数μsd，因此车轮纵向力应该表示为

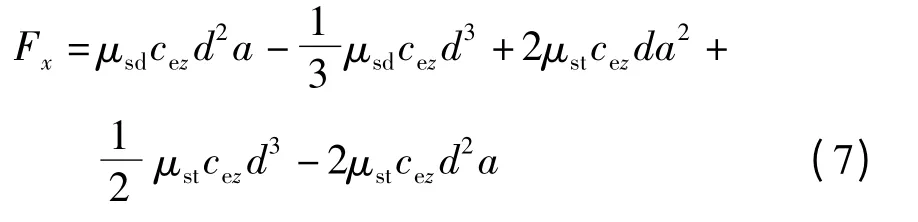
分析纵向附着区纵向力Fxt与滑移区纵向力Fxd对车轮纵向力的影响，可以将式(7)变为

式中，

通过大量的实验了解到充气轮胎的接地压力分布如下:中间胎面刚度小，内外两侧胎肩刚度大.故可以将cez和cex分别修正为中间和内外两侧的垂向刚度cez1、cez2之和，以及纵向刚度cex1、cex2之和，而且它们之间是并联关系.

根据轮胎尺寸设定特殊的“凹”路面，只让轮胎内外侧胎肩接触地面，测试内、外侧刚度.由于内、外侧胎面刚度和中间胎面刚度是并联关系，将总刚度减去内、外侧刚度就可得到中间刚度.

接下来，求解接地长度a 的表达式.如图5 所示，根据几何关系可得

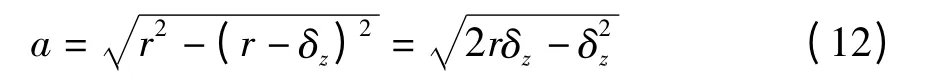
式中，

所以

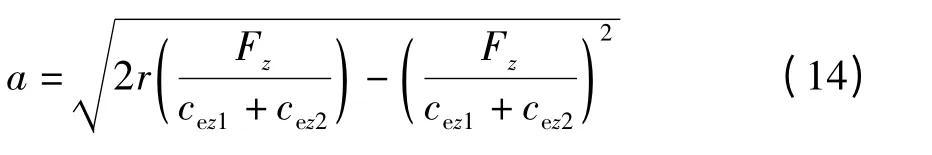
图5 接地印迹长度的求解Fig.5 Solving of the length of contact patch

由式(11)、(14)和(7)可得轮胎纵向力学表达式如下:

而且，此时纵向力Fx也应该是胎面纵向力Fxtr和胎肩纵向力Fxsh之和，即

其中，

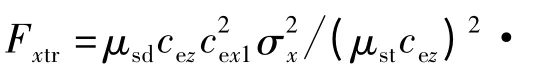
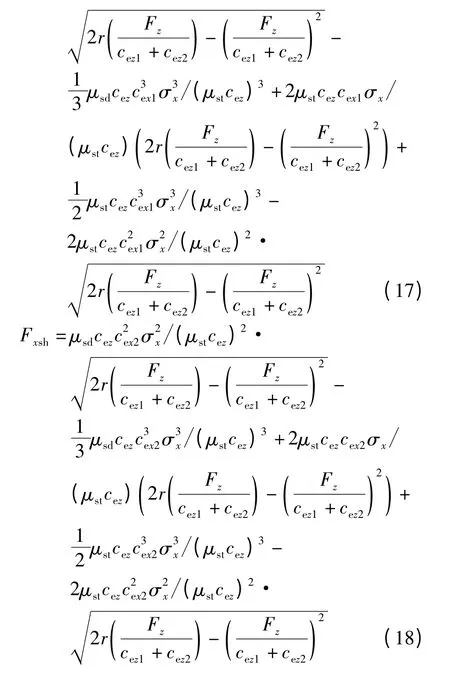
4 参数分析与实验验证

图6 为轮胎在接地区域的纵向力分布情况，由于轮胎静摩擦大于动摩擦，所以接地静摩擦圆在动摩擦圆外侧.刷毛纵向力Fex与静摩擦圆μstFez(x)曲线交点的横坐标xs为附着区与滑移区的分界点.

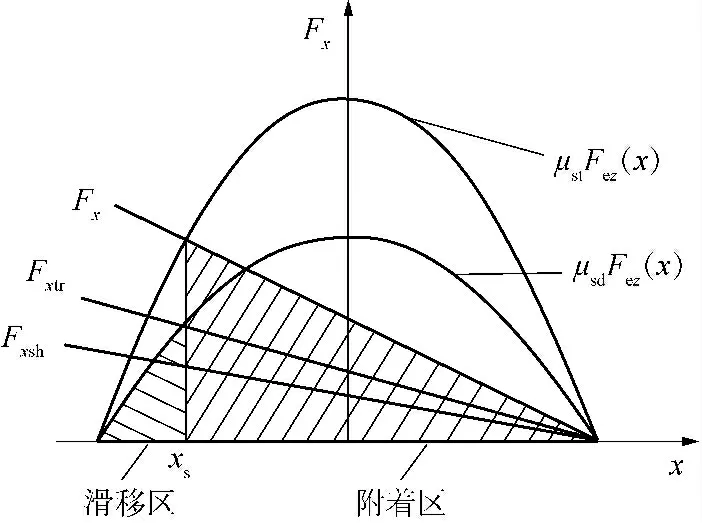
图6 轮胎接地区域的纵向力分布情况Fig.6 Longitudinal force distribution on contact patch of tire

从图7 所示纵向力的变化可以看出:轮胎纵向力Fx在滑移率σx为0.20 左右时取得最大值;滑移区纵向力Fxd随着滑移率σx增大而增大;附着区纵向力Fxt则有起伏，在σx为0.13 时取得最大值，随后降低;当滑移率σx在0.0～0.2 的区域内时，附着区纵向力Fxt占主导地位，随着滑移率的继续增大，Fxt逐渐减小，滑移区纵向力Fxd继续增大，并占主导地位.

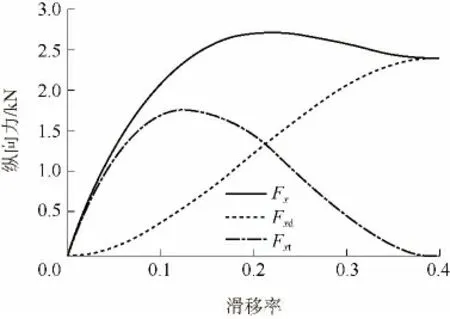
图7 Fx、Fxd和Fxt的变化情况Fig.7 Variation of Fx，Fxd and Fxt

由于假定胎面和胎肩刷子纵向变形量相同，从图8 可以看出，Fxsh和Fxtr的变化趋势一致，而且由于胎面接触面要大于胎肩接触面，Fxtr会大于Fxsh.

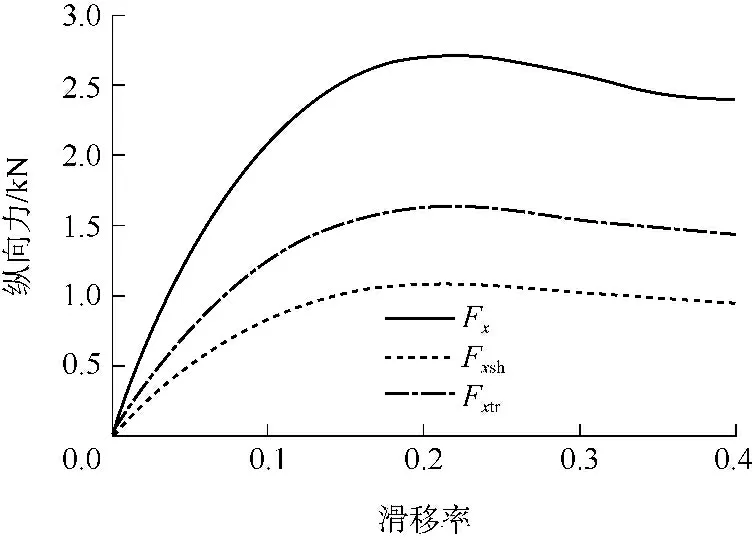
图8 Fx、Fxtr和Fxsh的变化情况Fig.8 Variation of Fx，Fxtr and Fxsh

图9 所示为不同纵向刚度下的纵向力，其中纵向刚度cex1下的纵向力最大，cex3下的纵向力最小，可见纵向刚度变大有利于增大纵向力极值，相应的滑移率也会降低.

图9 不同纵向刚度下的纵向力Fig.9 Longitudinal forces at different longitudinal stiffnesses

图10 所示为采用修正的刷子模型、魔术公式得到的纵向力与实验结果的对比.由图可见:随滑移率的增大，两种模型所得结果与实验结果在0.0～0.2 的滑移率区域内一致性较好，与σx成近似线性关系;随着滑移率的增大，模型结果与实验结果之间的差异增大，但误差可以接受，这主要是由于定义为常数的cex和cez会产生非线性变化，导致求解的xs产生误差，从而导致Fx的偏差变大.

图10 模型结果和实验结果的对比Fig.10 Comparison of the results obtained by models with the test ones

5 结语

文中通过对充气轮胎进行简化，利用轮胎力摩擦椭圆理论，根据轮胎接地的静态与动态附着状态，建立了附着区与滑移区的纵向力解析表达式;在此基础上，考虑胎面与胎肩刚度的不同，建立了修正的轮胎刷子模型.根据修正的轮胎刷子模型进行的轮胎力及其影响因素分析表明:随着滑移率的增大，滑移区动摩擦纵向力和附着区静摩擦纵向力的变化趋势具有明显差异;由于胎面与胎肩纵向变形量大致相同，胎面与胎肩的纵向力变化趋势基本一致，其合力为轮胎的纵向力;纵向刚度的增大会导致纵向力极值的增大，但是不会大于地面附着力.与魔术公式结果和实验结果的对比表明，文中提出的修正的轮胎刷子模型的纵向力表达式具有一定的可靠性，可以为轮胎力学特性的优化提供参考.后期还需要对各种类型轮胎进行大量试验，不断提高和完善模型的实用性.

［1］庄继德.汽车轮胎学［M］.北京:北京理工大学出版社，1996.

［2］臧孟炎，许玉文，周涛.三维非线性轮胎的五刚特性仿真［J］.华南理工大学学报:自然科学版，2011，39(1):129-133.Zang Meng-yan，Xu Yu-wen，Zhou Tao.Characteristic simulation of five kinds of stiffness of tire based on threedimension nonlinear model ［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(1):129-133.

［3］Guo K，Lu D.UniTire:unified tire model for vehicle dynamic simulation［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，2007，45(S1):79-99.

［4］Xu N，Guo K，Zhang X.UniTire model for tire forces and moments under combined slip conditions with anisotropic tire slip stiffness［J］.SAE International Journal of Commercial Vehicles，2013，6(2):315-324.

［5］Pacejka H B，Sharp R S.Shear force development by pneumatic tyres in steady state conditions:a review of modeling aspects［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1991，20(3/4):121-76.

［6］Sjahdanulirwan M.Yang Q.Prediction of tyre-road friction with an inverted-boat shaped stress distribution［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1995，24(2):145-161.

［7］Kung L E，Soedel W，Yang T Y.Free vibration of a pneumatic tire-wheel unit using a ring on an elastic foundation and a finite element model［J］.Journal of Sound Vibration，1986，107(2):181-194.

［8］Gim G，Nikravesh P E.An analytical model of pneumatic tires for vehicle dynamic simulations(part 1):pure slips［J］.International Journal Vehicle Design，1990，11(6):589-618.

［9］Gim G，Nikravesh P E.An analytical model of pneumatic tyres for vehicle dynamic simulations(part 2):comprehensive slip［J］.International Journal of Vehicle Design，1991，12(1):19-39.

［10］Guo K，Lu D，Chen S，et al.The UniTire model:a nonlinear and non-steady-state tyre model for vehicle dynamics simulation［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，2005，43(S1):341-358.

［11］Gim G，Nikravesh P E.A three dimensional tire model for steady-state simulations of vehicles ［M］∥SAE Technical Paper 931913.［S.l.］:Society of Automotive Engineers，1993.

［12］Bakker E，Pacejka H B，Lidner L.A new tire model with an application in vehicle dynamics studies［M］∥SAE Technical Paper 890087.［S.l.］:Society of Automotive Engineers，1989.

［13］Osamu Nishihara，Kurishige Masahiko.Estimation of road friction coefficient based on the brush model［J］.Journal of Dynamic Systems，Measurement，and Control，2011，133(4):041006/1-9.

［14］Pacejka H B，Bakker E.The magic formula tyre model［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1992，21(S1):1-18.

［15］Pacejka H B，Besselink I J M.Magic formula tyre model with transient properties［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1997，27(S1):234-249.

［16］Gordon T.Vehicle dynamics lectures notes［Z］.Ann Arbor:University of Michigan，2004.