非均质边坡光滑化处理及临界滑动面搜索

，

(重庆交通大学 土木建筑学院，重庆 400074)

1 研究背景

边坡的稳定性分析是岩土工程领域一个重要的研究课题，而极限平衡法则是边坡稳定性分析方法中应用最早、最广泛的方法。该方法运用Mohr-Coulomb强度理论，通过建立边坡处于极限平衡状态的静力平衡方程来求得问题的解。它不像有限元那样，引入应力-应变关系来求解本质上为静不定的问题，而是引入了一些简化假定，从而使问题变成静定可解。这些假定均需要事先对边坡进行条块划分，通过单个条块的2个力平衡方程消去条块底部的法向压力后，将不确定性加在条间力上，不同的条间力关系假定形成了不同的极限平衡法，如Janbu法、Spencer法和Morgenstern-Price法等[1]。

朱大勇等[2]在2002年提出了一种新颖的极限平衡法分析思路，通过一次插值逼近滑面正应力分布，最后导出了以安全系数为未知量的一元三次方程，该方法较之前的极限平衡法方程更为简洁，且理论更为严格，但该方法仍然要对滑体进行条分，此时条分的意义仅在于完成那些以滑体为积分域的域积分。后来郑宏等[3]对上述方法进行了改进，通过化域积分为边界积分，采用平衡条件的三力矩形式建立平衡方程组，提出了一种完全不需要条分的边坡整体分析法，并成功将其扩展到了三维边坡[4]。

由于传统的极限平衡条分法发展较早，目前针对边坡临界滑动面的搜索大多是借助于条分法结合智能算法展开的。如R.Baker[5]采用动态规划技术，结合Spencer法实现了滑面的搜索；K.S.Kahatadeniya等[6]采用蚁群算法得到了临界滑动面；高玮等[7]对采用路径搜索的蚁群算法引入奖惩策略，来克服其收敛速度慢和早熟收敛的缺点，得到了较好的效果；曹平等[8]基于混沌优化和复合形法联合搜索算法实现了较复杂边坡的临界滑动面搜索。

以上的滑动面搜索算法由于目标函数是滑面位置的非光滑泛函，只能借助于智能算法搜索，造成了计算效率的降低。孙聪等[9]对此问题进行了详细的介绍，且提出了一种基于整体分析法的滑动面搜索技术，该方法将安全系数看成与滑面坐标点同等的独立变量，目标函数即是安全系数本身，成功地运用经典优化算法——牛顿法实现了滑动面的搜索。但文中只是对均质边坡进行了详细讲解，实际公路、铁路等边坡工程中，最常见的还是非均质边坡，由于非均质边坡的材料参数不均匀，必然会导致边坡应力场在材料交界面发生间断，以至于无法对以应力场为自变函数的安全系数直接使用带梯度信息的优化算法。针对此问题，本文提出了一种非均质边坡光滑化处理方法，成功实现了基于整体分析法的非均质边坡临界滑动面搜索。

2 整体分析法介绍

设滑体Ω是由边坡外轮廓线g和某一潜在滑面s所围成的平面区域，滑体内可以包含多种介质，如图1所示。取整个滑体Ω为受力体，其所受到的主动力有体积力(包括自重和水平地震力)和作用在外轮廓线g上的面力或集中力，其所受到的约束反力为滑面上的正应力σ(x)和切向应力τ(x)。

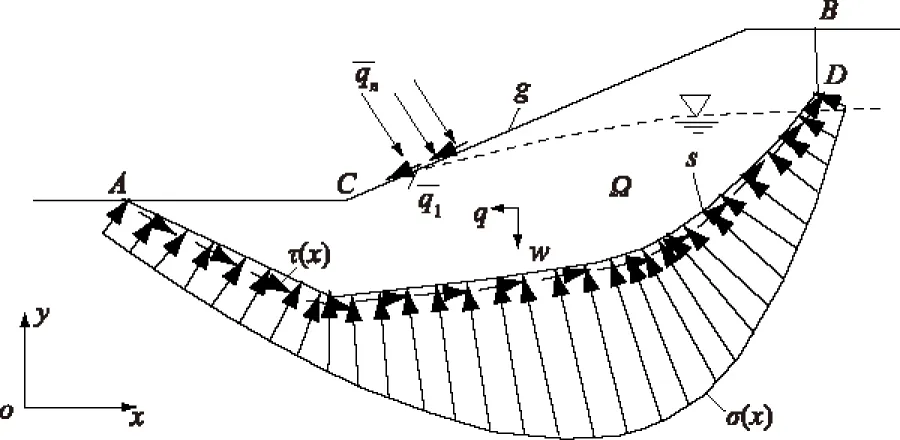
图1 滑体及作用其上的力系

(Δxciτ+Δyciσ)dy+mci=0。

(1)

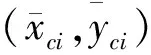
(2)

其中，

cw≡ce-feu。

式中：F为安全系数；ce和fe均为有效抗剪强度参数；u为孔隙水压力。

滑面上任一点的法向正应力σ可表示为

σ=σ(x)=σ0+σ′ 。

(3)

式中：σ′和σ0分别表示来自条间力和滑体上的外荷载对滑面正应力的贡献，都是坐标x的函数。σ0可以通过坡体的特征求出，是已知的。而式(3)中的σ′未知，可以通过构造一个修正函数来进行逼近：

σ=σ0+f(x;a1,a2) 。

(4)

式中：f(x;a1,a2)为滑面应力修正函数，之所以引入2个待定参数a1和a2是因为仅有3个平衡方程，只能用来求解3个未知数，而安全系数便是其中一个。可以将此修正函数定义为线性函数：

f(x;a1,a2)=a1la1(x)+a2la2(x) 。

(5)

其中，

(6)

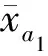
将式(2)至式(4)代入式(1)，即得只有3个未知数(F，a1和a2)的3个平衡方程，对这3个方程进行牛顿法求解，求得的F即为边坡的安全系数。

3 优化模型建立

在滑面上布置一定数量的插值点(xi，yi)对滑面进行离散，这些点可以看成构成滑面的控制点，将这些点顺序用直线段连接即可逼近滑动面。在优化过程中可以固定这些点的xi坐标，而仅仅使yi坐标发生变化。为了降低问题的非线性程度，这里把安全系数F作为独立自变量看待，将目标函数定义为

G(F,y,a) =F。

(7)

即G(F,y,a)不依赖于y和a。这样一来，就克服了以往仅以滑面位置和应力插值系数a为自变量导致的强非线性问题。

一般情况下，除了3个力矩平衡方程之外，还需考虑滑面的特性，加入其它一些必要的不等式约束，如滑面凸性：

yi+λjyk≥(1+λj)yj。

(8)

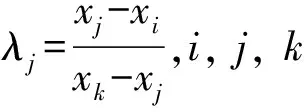
综上所述，整个优化模型可表示为

(9)

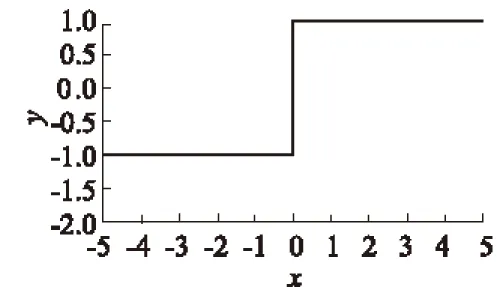
图2 Heaviside函数图形

4 非均质光滑化逼近

对于非均质边坡，由于材料在交界面上发生间断，使得坡体内部应力场发生不连续，这就给直接使用经典优化算法带来了困难。对于间断问题，可以采用Heaviside函数表示，如图2所示；当然，对于非均质边坡带来的材料间断也可以用该函数进行表示。

为了使Heaviside函数具有光滑性，采用如下函数对其进行逼近(见图3)：

(10)

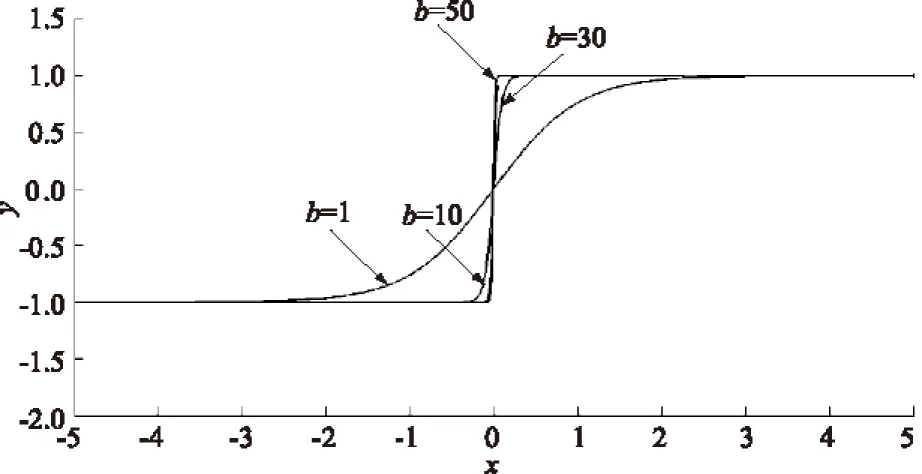
图3 拟合函数示意图

本文将黏聚力c和内摩擦角φ先用符号函数分别写成一个整体表达式，再用上述连续函数进行拟合，从而得到一个整体连续光滑的函数，这样在进行滑面搜索时边坡内部材料参数的形式便得到了统一。

5 算例验证

以下2个算例分别为澳大利亚计算机应用协会(ACADS)对澳大利亚所使用的边坡稳定分析程序进行考察的考核题3(b)和1(c)[10](文中分别简称其为考核题1和2)，为典型的公路边坡，且均是采用Matlab自编软件进行计算。

5.1 含软弱夹层的边坡

某一均质边坡中间有一厚为0.5 m的软弱夹层，土坡材料参数见表1，边坡模型见图4(a)。

表1 含软弱夹层土坡材料参数

图4 考核题1中本文方法与其他各家方法搜得的临界滑面对比

本例题在坡面下方布置了67个离散点，迭代80次达到收敛，最终滑动面形状如图4(a)所示，安全系数F=1.266 5。图4(b)是摘自文献[10]中各家对此问题求解的安全系数结果。

从图4(b)中可以看出，不同方法搜出的滑动面形状有较大差异，安全系数在1.19～1.82范围内，而本文方法搜得的滑动面与图4(b)中基于Spencer法搜得的安全系数F=1.24的滑面形状较为一致，且安全系数也较为接近，只是本文方法的滑动面底部略宽。

针对本算例，将材料参数光滑化处理步骤说明如下(以黏聚力c为例)：

c在y=27时产生间断：

(11)

本文的约束条件是根据整体分析法求的，此方法以整个滑体而不是单个条块为研究对象，不引入条间力，将域积分转化成了边界积分，所以此处不关心y= 27时c的取值，因为曲线积分只对某一个点来说是没有意义的。这时，用符号函数可表达为

(12)

此时式(12)仍是间断的，再对其进行光滑化拟合，且b取30，可以写成：

(13)

式(13)的几何图形如图5所示。

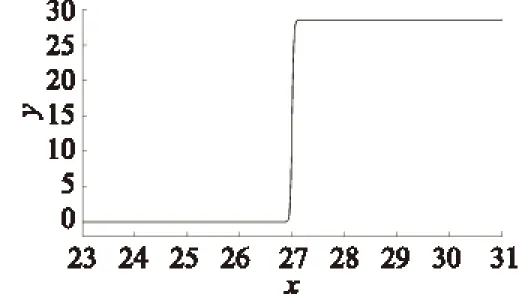
图5 b=30时式(13)的几何图形

5.2 典型公路非均质边坡

一分层边坡，形状如图6(a)所示，材料参数见表2。

本例题在潜在滑面上布置了51个离散点，迭代76次达到安全系数F收敛于1.388 1，滑动面形状如图6(a)所示。

表2 非均质土坡材料参数

图6(b)为不同方法对此算例滑动面搜索结果，安全系数介于1.287和1.52之间，通过对比发现，安全系数同为1.39的Spencer法和Bishop与本文方法搜得的滑动面比较一致，再一次说明本文方法的可靠性。

图6 考核题2中本文方法与其他各家方法搜得的临界滑面对比

6 结 语

针对非均质边坡内部材料参数不连续问题，通过函数逼近的方式进行光滑化处理，使得边坡内部应力场光滑连续，这就给直接利用经典的基于梯度信息的优化算法来寻找边坡临界滑动面提供了可能。借助于边坡稳定性的整体分析法，把安全系数看成与滑面离散点坐标同等的独立变量，目标函数即是安全系数本身，实现了非均质边坡的临界滑动面搜索，为后续的边坡支护提供帮助。文末的2个算例说明了本文方法的正确性。

参考文献：

[1] DUNCAN J M. State of the Art: Limit Equilibrium and Finite Element Analysis of Slopes[J]. Journal of Geotechnical Engineering, ASCE,1996, 122(7):577-595.

[2] ZHU D Y, LEE C F. Explicit Limit Equilibrium Solution for Slope Stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(15): 1573-1590.

[3] ZHENG H, THAM L G. Improved Bell’s Method for the Stability Analysis of Slopes[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(14): 1673-1689.

[4] 郑 宏. 严格三维极限平衡法[J]. 岩石力学与工程学报, 2007,26(8):1529-1537. (ZHENG Hong. A Rigorous Three-dimensional Limit Equilibrium Method[J]. Chinese Journal of Rock Mechanics and Engineering，2007，26(8):1529-1537. (in Chinese))

[5] BAKER R. Determination of the Critical Slip Surface in Slope Stability Computations[J]. International Journal of Numerical and Analysis Methods in Geomechanics，1980，4(4)：333-359.

[6] KAHATADENIYA K S, NANAKORN P, NEAUPANE K M,etal. Determination of the Critical Failure Surface for Slope Stability Analysis Using Ant Colony Optimization[J]. Engineering Geology，2009，108(1/2)：133-141.

[7] 高 玮,张鲁渝,张飞君. 边坡临界滑动面搜索的奖惩蚁群算法研究[J]. 水利学报,2012，43(2):209-215. (GAO Wei, ZHANG Lu-yu, ZHANG Fei-jun. Critical Slip Surface Searching for Slope Based on Premium-Penalty Ant Colony Optimization[J]. Journal of Hydraulic Engineering, 2012, 43(2):209-215. (in Chinese))

[8] 曹 平,张 科,汪亦显，等. 复杂边坡滑动面确定的联合搜索法[J]. 岩石力学与工程学报，2010，29(4)：814-821. (CAO Ping, ZHANG Ke, WANG Yi-xian,etal. Mixed Search Algorithm of Critical Slip Surface of Complex Slope[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(4): 814-821. (in Chinese))

[9] 孙 聪, 李春光, 郑 宏. 基于整体分析法的边坡临界滑动面搜索[J]. 岩土力学，2013, 34(9):2583-2588. (SUN Cong, LI Chun-guang, ZHENG Hong. Location of Critical Slip Surfaces Based on the Global Procedure for Slope Stability Analysis[J]. Rock and Soil Mechanics, 2013, 34(9): 2583-2588. (in Chinese))

[10] 陈祖煜. 土质边坡稳定分析——原理、方法、程序[M]. 北京：中国水利水电出版社，2003:365-376. (CHEN Zu-yu. Stability Analysis for Soil Slope: Principle, Method and Program[M]. Beijing: China Water Power Press, 2003: 365-376. (in Chinese))