基于马尔科夫链的体育教学评价研究

朱玉霞,李星祥

(1.南京信息工程大学 体育部，江苏 南京 210044；2.南京信息工程大学 研究生院，江苏 南京 210044)

本文通过改进马尔科夫链教学评价模型，并将其应用到体育教学评价中来，希望能更客观地描述学生体育学习的进步幅度、发展情况，并能对体育教学效果进行客观的评价。

1 马尔科夫链在体育教学评价中的应用步骤

马尔科夫链在体育教学评价中的应用是建立在两次体育测试成绩的结果上的，通过比较第一次测试与第二次测试处于不同成绩等级上的学生人数的变化，构建转移概率矩阵。假定保持体育教学效果稳定的前提下，经过多个阶段的体育教学后，利用马尔科夫链的稳定分布状态可以得到学生最终成绩的分布状态。具体步骤如下：

(1)将一个教学单位(班级或者学院)的第一次体育测试成绩划分为r个等级，设参加体育测试的学生总人数为n，处于第i个等级的学生有ni个(i=1,2,…,r)，计算第一次测验后学生体育成绩分布的初始向量，用A(0)表示：

(1)

(2)经过一段时间的体育教学后对学生进行第二次体育测试，依据上述的方法，可以得到第二次测试中每个等级的学生数ni(i=1,2,…,r)，由此可以得到A(1)，还可以分别得到所有第i个等级转移到第j个等级的学生数目nij(i,j=1,2,…,r)，由此可以构造转移概率矩阵P为：

(2)

2 马尔科夫链在体育教学评价中的应用

2.1 模型的改进

利用马尔科夫链对体育教学进行评价时，通常利用前后两次体育测试成绩之间的联系来刻画转移概率矩阵，并由此计算稳定状态A来刻画体育教学成果。但是，通常大学体育教学中前后两次测试的项目和季节环境会存在差异，这会造成前后两次测试划分的等级不具有可比性。现以某高校一个班级前后两次体育测试为例来说明以上情形，已知第一次体育测试的平均成绩为85分，标准差为5分，且在[90,100]的有10人，在[80,90)的有14人，在[70,80)的有13人，在[60,70)的有2人，在[0,60)的有1人。在第二次体育测试中，平均成绩为88分，标准差为10分。第一次体育测试成绩在第二次体育测试成绩中的分布情况见表1。

表1 两次体育测试对比

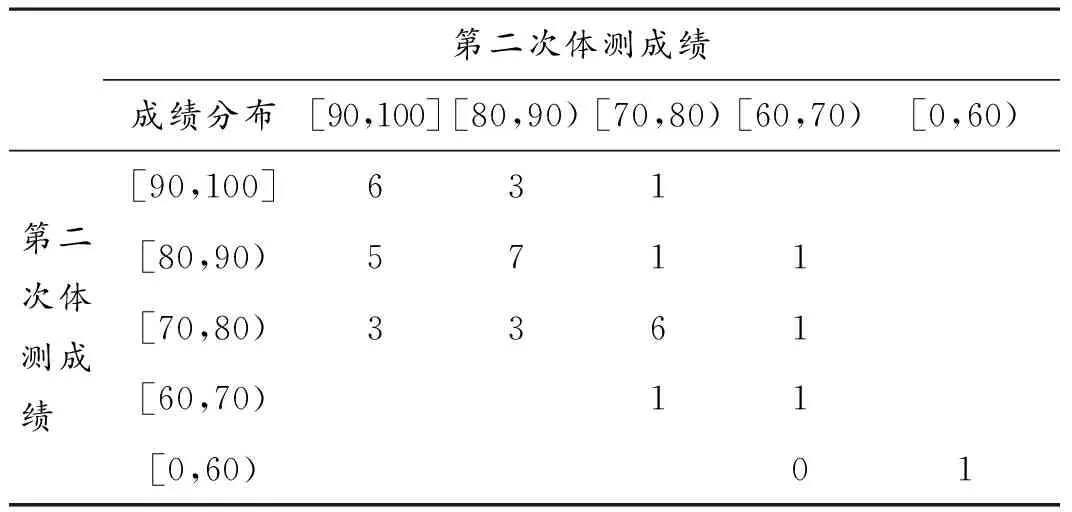
第二次体测成绩成绩分布[90,100][80,90)[70,80)[60,70)[0,60)第二次体测成绩 [90,100]631[80,90)5711[70,80)3361[60,70)11[0,60)01

若将两次体育测试成绩均转化为“标准分”，“标准分”的转化公式为：

(3)

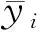
表2 两次体育测试“标准分”对比

第二次体测成绩成绩分布[0.2,1.2][-0.8,0.2)[-1.8,-0.8)[-2.8,-1.8)[-8.8,-2.8)第二次体测成绩[1,3]631[-1,1)5711[-3,-1)3361[-5,-3)11[-17,-5)01

由表2可以看出，前后两次体育测试成绩分布是不等值的，第一次体育测试的5个等级与第二次体育测试的5个等级不具有可比性，而这一点可从两次测试项目和季节环境的差异来得到解释。所以传统情况下根据体育测试得分[90,100]、[80,90)、[70,80)、[60,70)、[0,60)来划分状态在均值和方差不相等的状态下是不够合理的。

鉴于传统划分等级方法的不足，本文利用公式(3)将学生体育测试得分全部转化为“标准分”，在此基础上来划分等级，构造转移矩阵。使用标准分的好处是模型有效避免了因体育测试项目和季节环境的不同而造成的分类等级不可比的问题。需要特别指出的是，当进行多个班级体育教学质量评比的时候，学生成绩“标准分”公式为：

(4)

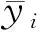
考试成绩r个等级的合理划分是构造有效转移矩阵的基础，本文参考标准正态分布的分位数点来确定等级划分标准。学生体育测试得分大体上服从正态分布，故“标准分”大体上服从标准正态分布，所以考试成绩r个等级划分的标准可以参考标准正态分布的分位数点。例如，若要选取前25%的学生为第一等级，那么第一等级学生的标准分应大于0.675，0.675为标准正态分布函数的四分之三分位点；选取前25%～50%的学生作为第二等级，那么第二等级学生的标准分应处于0至 0.675之间，0为标准正态分布分函数的二分之一分位点；选取前50%～90%的学生作为第三等级，那么第三等级学生的标准分应处于-1.28至0之间，-1.28为标准正态分布函数的十分之一分位点；最后10%的学生处于第四等级，他们的标准分小于-1.28。

2.2 建立教学评比模型

在进行体育教学评比时，有两件事情值得关注，一是最终学生体育成绩的稳定分布A，二是学生体育成绩的进步幅度。假设以后的教学效果不发生改变，即转移概率矩阵保持平稳不变，那么通过解方程，可以计算出反映学生最终体育成绩分布的稳定状态向量A=(a1,a2,…,ar)。基于如此考虑，本文构造了一个衡量学生体育成绩进步幅度的评价函数：

2.3 实证分析

本文选取南京信息工程大学2012级两个班级作为测试对象，以两班学生在2012-2013年度两个学期的体育测试成绩进行体育教学评价，体育测试的项目和时间一样，两个班级分别记作甲和乙，每班30位学生。通过使用公式(4)将两个班的学生体育测试成绩转换成“标准分”，然后按标准分的大小分成[0.675,∞)、[0,0.675)、[-1.28,0)、(-∞,-1.28)4个等级。

接着，计算两个班级体育成绩分布的转移概率矩阵，分别记为P甲和P乙：

然后，计算两个班级体育成绩分布最终的平稳状态向量，分别记为A甲和A乙：

A甲=(0.44,0.24,0.32,0)
A乙=(0.42,0.42,0.14,0.02)

最后，为了鼓励学生积极参加体育锻炼，本文设定wi=(50,30,10,5)，算出两个班级的进步幅度，分别记为F甲和F乙：

F甲=5.87，F乙= 13.77

假设以后的教学效果保持不变，从学生体育成绩的最终分布可以看出，班级甲将有44%的学生体育成绩处于等级一，24%的学生体育成绩处于等级二，低于处于等级三的有32%，等级四将趋于0；班级乙将有42%的学生体育成绩处于等级一和等级二，等级三的学生比例降至14%，等级四趋于2%。从各个等级学生成绩的分布来看，班级乙的体育成绩分布将优于班级甲。从体育成绩的进步幅度上来看，班级乙的体育成绩进步幅度大于班级甲。从两个班级体育成绩的初始分布来看，在初期班级甲体育成绩分布优于班级乙，但是随着各班体育教学的深入，班级乙的体育成绩进步明显，且对班级甲实现了超越。最后可以得出结论，班级乙的学生体育学习效果优于班级甲。

3 结论

通过对马尔科夫链进行改进，本文提出了一种关于教学质量、教学效果比较评价的有效方法。经过改进的马尔科夫链体育教学评价模型，可有效避免因为体育测试项目和季节环境不同而造成的分类状态不可比的问题，同时在教学评比时将所有学生的成绩放在了同一个标准下进行评比，将更有利于得到公平客观的评比结果。划分等级时，本文参考了标准正态分布的分位数点来确定等级划分标准，使等级划分更加合理，将有利于构造更加有效的转移概率矩阵。用所构建的体育成绩进步幅度函数来评比不同班级的教学成果，量化了整个班级的体育成绩进步幅度。在教学效果保持不变的情况下，改进的马尔科夫模型可以预测班级体育成绩将会达到的分布状态以及进步幅度大小，这对于教师在现阶段的教学有着很好的导向和提醒作用，有助于体育教学工作更加科学有效地发展。

[1] 黄少罗,张武军,张殿亮,等.马尔可夫链在体育教学效果评价中的应用[J].河北师范大学学报，1999(1):134-137.

[2] 黄宝宏,孙健，魏登云.马尔可夫(Markov)链在体育教学评价中的应用改进[J].天津体育学院学报，2005(2):33-35.

[3] 刘鲁文,陈兴荣,何涛.基于马尔科夫链的教学效果评估方法[J].统计预测与决策，2014(3):93-94.

[4] 刘旼航，邵桂华，孙庆祝.基于马尔柯夫链的体育教学质量模糊评价方法[J].西安体育学院学报，2006(1)：108-110.