连线干涉测量体制误差因素分析*

路伟涛 杨文革 洪家财

装备学院 ，北京101416



连线干涉测量体制误差因素分析*

路伟涛 杨文革 洪家财

装备学院 ，北京101416

针对连线干涉测量体制(Connected Elements Interferometry， CEI)的特点，首先详细分析了CEI数，推导了电离层误差和对流层误差等信道误差的表达式；然后采用极限分析的方法，得到了CEI角度测量的最佳精度，并给出了基线长度设置建议。当基线较短时，时钟同步误差最大；当基线增长时，电离层误差等信道误差是主要误差因素。综合考虑误差因素和成本问题，基线长度设置为10km左右比较合适。

连接线干涉测量；系统误差；信道误差；基线长度

连线干涉测量(CEI)技术通过测量站间载波或侧音的相位差实现时延测量，理论上可以达到很高的精度[1-2]，相对于甚长基线干涉测量而言(其测角精度达到了2～5nrad，甚至更高[3])，是一种中精度角度测量系统。CEI系统以其较高的测角精度、较强的实时性等诸多优点在航天测控中具有独到的应用价值，对误差因素的分析有比较重要的意义。首先，误差因素的分析可以用于确定系统先验延迟模型的精度，从而影响载波时延整周模糊解算；其次，对误差因素的分析可以统计各种误差因素影响的大小，以在有限的误差容限内或者一定测量精度要求下作系统误差分配，进而给出参数设置的建议。一般误差因素可以归结为3类：模型误差、信道误差和系统误差。模型误差包括引力场模型误差、力学模型误差[4]等；信道误差是指不同测站的接收信号因路径不同而引起的误差，包括大气误差、电离层误差、太阳等离子体误差等，关于此类误差研究比较深入，也提出了应用广泛的修正模型[5-7]；系统误差包括测站间的时钟误差、测站位置误差、设备相位抖动误差等。

由于CEI基线比较短，在一定程度上可以对消2个测站的信道误差，如对流层误差、电离层误差等，这也是CEI相对VLBI的优势之一。虽然如此，该部分误差因素仍需进行分析。在国内外文献中误差分析部分多侧重于ΔVLBI系统，而且一般以经验公式或者通过仿真分析给出相应误差因素的影响[8-10]，却未从理论上进行分析，这对误差因素的理解和消除不利。

本文在侧重考虑时钟同步误差、频率稳定度、基线误差、设备相位抖动和基站定向误差等系统误差的同时，也分析了对流层误差和电离层误差等信道误差。

1 系统误差因素分析

1.1 时钟同步误差

不同测站之间的时钟需要同步以使数据记录的时刻相同。但由于同步精度有限、记录设备同步触发脉冲抖动等，各测站之间仍然存在时钟同步误差，这将直接影响站间时延测量结果。

设测站i(i=1,2)的相位为φi，主值为φi，模糊度为Ni；假设测站2与测站1存在时钟同步误差ετ，则

φ1=φ1+2πN1,φ2=φ2+2πN2+2πfδτ

(1)

可以得到差分相位为：

Δφ21=φ2-φ1+2πN21+2πfετ

(2)

其中N21=N2-N1。继而可得时钟同步误差引起的时延测量误差为：

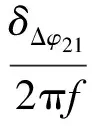
(3)

由式(3)可以看出时钟同步误差将直接影响时延差的测量结果。目前时钟同步方式主要有GPS卫星共视法[11]、卫星双向比对法[12-13]和光纤连接法[14-15]等。对于GPS卫星共视法时间同步精度可以达到5～10 ns；卫星双向比对法时间同步精度优于1ns；光纤传递法可以实现0.1ns或更低(0.0252 ns)的时间同步精度。考虑到光纤传输的特点、时间同步精度以及CEI站间距较短的特点，采用光纤传输时间和频率是目前CEI系统通常的做法。

由于目前测站时钟稳定度较高，还可以借鉴ΔVLBI的数据处理方式，通过观测位置精确已知的射电源进行时钟误差消除。此时时钟同步误差由下所示：

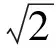
(4)

其中，Δf/f为阿伦方差，Tobv为观测间隔。假设阿伦方差为10-14，观测间隔为2 min，则由此引起的时钟同步误差为1.6968 ps。

1.2 频率误差

(1)频率同步误差

设两天线的接收信号分别为：

(5)

信号经过下变频、中频传输,到达接收机通道后的信号为：

(6)

由此可以得到2个信号的相位差为：

Δφ(t)=-2πfτ+2π(fLO2-fLO1)t+φ2-φ1=-2πfτ+2πΔfLOt+Δφ21

(7)

由此可以看出2个测站本振差在积分时间内的相位积累全部转化成时延量，即：

στ=ΔfLOTp/fBW

(8)

其中，Tp为积分时间，fBW为信号带宽，对于CEI的载波相位测量fBW应为射频频率。采用光纤传递法，两站相对频差约为4.8×10-14，由此可得由两站频率同步误差引起的时延差为0.047ps。

(2)频率稳定误差

频率稳定误差是由于频率不稳定性(频率源的阿伦方差)引起的。设tc,i为测站i时刻(i=1,2)，ω0,i为测站i真实频率，ωc,i为相应的标称频率，由于ωc,i与ω0,i不可能完全一致，假设ω0,i=ωc,i+Δωc,i,那么在真实时刻ti相对于参考时刻t0，相位真实的变化量φc,i由真实频率决定：

φc,i=ω0,i(ti-t0)=(ωc,i+Δωc,i)(ti-t0)

(9)

由相位的变化量和标称频率可得出时间变化：

tc,i=φc,i/ωc,i=(ωc,i+Δωc,i)(ti-t0)/ωc,i

(10)

设tc,i=ti+τc,i，t0=0，那么可以得到：

τc,i=(Δωc,i/ωc,i)ti

(11)

其中,Δωc,i/ωc,i为测站i的频率稳定度。

由此可得2个测站的时延差τc：

τc=tc1-tc2=t2-t1+(Δωc2/ωc2)t2-
(Δωc1/ωc1)t1

(12)

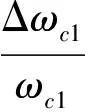
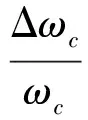
(13)

可知,由两站钟差引起的误差δτ与两站的时延差τ有关：

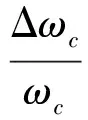
(14)

若采用光纤无补偿传输，频率的阿伦方差为3×10-14/s；有主动相位补偿时，稳定度可以提高1～2个量级[16]。CEI基线长度B为20km，入射角θ为60°，那么由此引起的时延误差约为1×10-6ps。同时考虑到在实际数据处理过程中需要进行长时间的积累，这对频率稳定度也提出了要求。假设积累时间Tp=1s，那么由式(14)可以得到：

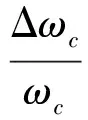
(15)

计算可得在积分时间内由于频率不稳定引起的时延误差为0.03ps。综合考虑频率同步误差和稳定误差可得频率误差影响为0.0575ps。

1.3 基站定向误差

由于角度的测量是由信号到达地面两测站的时间差来推算的，因此测站位置和地球定向的不确定性将会影响测量值的精度。地极定向和自转速率随机变化，必须进行监视以保证对这些参数的了解。目前JPL通过对实时数据的分析，可将地球定向估计误差控制在30cm以下；将分析的数据长度增加到两周，则可将误差降低到5cm。通过VLBI测量和卫星雷达测距，美国深空网(DSN)测站位置的测量精度可达到5cm，则由基线测量误差引入的测量误差为：

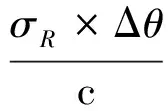
(16)

其中，Δθ为观测目标相对基线形成的张角，单位urad；σR为测站位置和地球定向的不确定性而引入的测量误差，单位mm，保守考虑设为70 mm；c为光速，单位km/s。设入射角为60°，CEI基线长度B为500m，对于同步轨道卫星Δθ约为12.0281 urad，那么由基线测量误差引起的时延误差约为0.0028ps。当基线长度增加到10km和100km时，基线误差增大到0.0568 ps和0.5679 ps。

1.4 设备相位抖动

CEI使用侧音相位差观测进行时延估计，设备的相位抖动只在侧音频率处产生影响，同时考虑到两站通过相位差分求取时延，其大小如式(19)所示[17]：

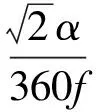
(17)

假设设备相位抖动0.2°，对于带宽为38MHz的VLBI观测，引起的误差为29.5 ps；而同样的设备相位抖动对于S频段(2.2 GHz)DOR信号的CEI系统，引起的误差为0.3571 ps。

2 信道误差因素分析

2.1 对流层误差

对流层是高度为40km以下的大气层。由于其离地面近，大气密度较大且大气状态随地面气候而变化。电磁波通过对流层时，传播速度发生变化而引起传播延迟误差。假设ρpeak为天顶方向的对流层延迟路径差，EA和EB分别表示2个测站到观测目标卫星的仰角，则2个测站在目标视线方向的对流层延迟误差为：

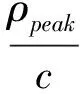
(18)

CEI在测量高轨卫星时,EA，EB近似满足EB=EA+Δθ，由于Δθ一般比较小，所以此时对流层延迟误差具有一定的相关性，经过差分处理后可在一定程度上对消，那么残留误差可表示为

(19)

取对流层延迟误差ρpeak为映射到较低仰角上的极值0.04m[18]。对于同步卫星，若Δθ约为12.0281urad，由式(19)可得对流层延迟误差为0.0011ps；若基线为10km，则Δθ约为240.5626urad，此时对流层延迟误差约为0.0214ps；若基线为100km，则Δθ约为2405.6261urad，此时对流层延迟误差约为0.2138ps。

2.2 电离层误差

电离层分布于地面向上60～1000km的范围，含有大量的带电粒子。电磁波穿过电离层时传播速度和传播路径会发生变化，变化程度主要取决于电离层的电子密度和电磁波频率。但目前无法从理论上给出TEC与各种影响因素之间准确的函数关系式，所以电离层延迟改正一般利用双频改正的方法能够获得比较精确的修正。这里分析CEI测量中电离层引起的测量误差。

对于单个目标，电离层引起的时延误差为：

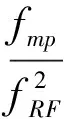
(20)

其中,TECz是天顶延迟，单位1016el/m2(TEC单位)；fmp是从天顶方向到视线方向的映射函数；fRF是射频频率，单位GHz。经过站间差分操作，2个目标对于同一测站，电离层时延误差为：

(21)

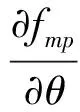
(22)

可以看出电离层误差与Δθ有关。假设信号为S频段(载波为2.2GHz)，若基线为500m，对于同步轨道卫星Δθ约为12.0281 urad，由式(22)可得电离层延迟误差为0.1149 ps；若基线为10km，则Δθ约为240.5626 urad，此时对流层延迟误差约为2.2924 ps；若基线为100km，则Δθ约为2405.6261urad，此时对流层延迟误差约为22.9240 ps。

表1给出了CEI测量中各项误差因素的影响，其中时延误差单位为 ps。由表1可以看出，当基线较短时，设备相位抖动误差影响最大，其次为时钟同步误差和电离层误差；当基线增长时，电离层误差和对流层误差影响增大，其中电离层误差成为主要误差源。这一结论与CEI测量体制特点相符，当基线较短时，目标相对两站的信道误差较小；当基线增长时，信道差异增大，电离层误差等信道误差影响增大。

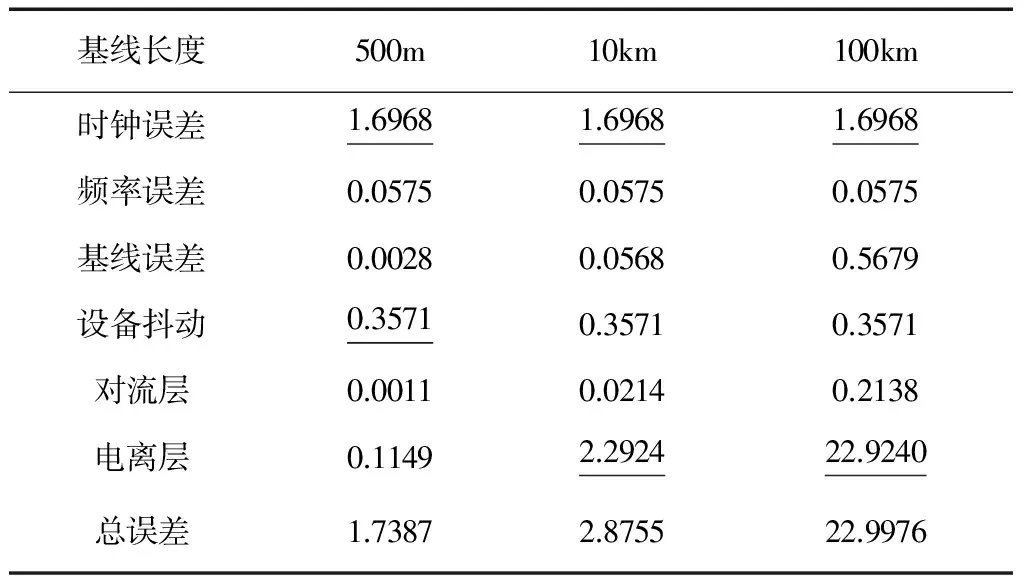
表1 CEI各项误差分析(ps)

2.3 基线长度分析

由干涉测量原理可知，测角精度与基线长度成正比，即基线越长，测角精度越高。考虑到基线增长，信道误差影响增大。综合两方面因素可给出测角意义下的基线最佳长度设置。由表1结果可得系统误差约为1.7349 ps(表中时钟误差、频率误差和设备抖动的综合误差)，假设载波时延测量误差为0.5 ps(约1/100射频周期，载波频率2.2 GHz)，再考虑电离层误差和对流层误差，可得总误差如式(25)所示，其中στp,στSys,στB,στIon,στTrop分别为载波时延测量误差、系统误差、基线误差、电离层误差和对流层误差。

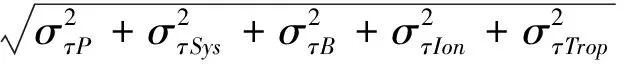
(23)

式(23)是在考虑系统误差、信道误差和时延测量误差时S频段(2.2GHz)同步卫星的测角精度，其中θ为天线仰角(目标方位角)，单位rad；B为基线长度，单位m。由式(23)可得测角精度公式：

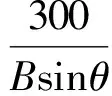
(24)

当基线长度增大时，由式(24)可以得到测角误差的下限：

(25)

由此可得不同方位角θ下的测角精度上限。假设方位角θ分别为30°，45°和60°，由式(25)可得测角精度下限分别为0.0798686 urad，0.0797912 urad和0.0797792 urad。

下面通过数值仿真考察不同基线长度下的测角精度，如图1所示。由图1(a)和(b)可以看出随着基线增长，测角精度呈下降趋势；方位角越大，测角精度越高；3种方位角(30°，45°和60°)下,基线长度由0.5km增加到10km时,测角精度分别由精度上限的10.0809%，14.1712%，17.2670%增加到89.6760%，94.4073%，96.1650%，此时基线增长，对测角精度的改善比较明显，改善幅度高达80%左右。而当基线长度由10km增加到100km以及由100km增加到500km时，3种方位角下测角精度的改善幅度分别为10.2025%，5.5317%，3.7944%以及0.1167%，0.0585%，0.0390%。

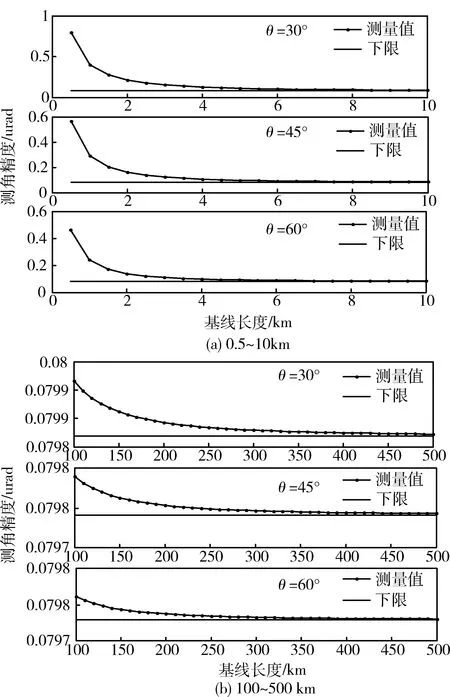
图1 不同基线长度下测角精度

上述理论和仿真结果是在基线增加时系统误差和载波时延测量误差几乎不变的前提下得到的。实际上,随着基线的增长，系统站间时钟同步性能、频率同步性能等系统性能会有所恶化，载波时延测量精度也会有所降低，那么基线增长引入的误差较上述分析结果要大，基线增长对测角精度的改善幅度也相对较低。因此，综合考虑各种误差因素和基线增长引起的成本问题，选择基线长度为10km左右是比较合适的。

3 结语

1)对CEI测量误差因素进行了理论分析。考虑到CEI干涉测量体制的特点，详细分析了CEI对GEO等高轨卫星测量时的系统误差和信道误差。系统误差主要包括时钟误差、基线误差、设备相位抖动误差等。以目标相对基线的张角为参数，对电离层误差和对流层误差等信道误差进行了定量分析。当基线较短时，时钟同步误差最大，其次为设备相位抖动误差和电离层误差；当基线增长时，电离层误差等信道误差逐渐增大，成为主要误差因素。

2)提出了基线长度设置建议。在综合考虑测量误差、系统误差、信道误差等因素的基础上，给出了CEI的测角精度公式；然后采用极限分析法得到了CEI的角度最佳测量精度;最后给出了基线长度设置建议。

[1] Thurman S W. Information Content of a Single Pass of Phase-Delay Data Forma Short Baseline Connected Element Interferometer [R]. TDA Progress Report 42-101, 1990,42(101):26-38.

[2] Edwards C D. Short Baseline Phase Delay Interferometry[R].TDA Progress Report 42-91, 1987：46-56.

[3] Wood L J.The Evolution of Deep Space Navigation: 1989-1999 [R].AAS 08-311, Guidance, Navigation, and Control Section, Jet Propulsion Laboratory, California Institute of Technology.

[4] 李晓杰，黄金，潘玲.改进单组CEI基线对卫星定轨精度的影响研究[J].海洋测绘, 2010, 30(4):5-8.(Li Xiaojie, Huang Jin, Pan Ling. The Method of Improving Single Group CEI Baselines-based Orbit Determination for Geostationary Satellite [J]. Hydrographic Surveying and Charting, 2010， 30(4):5-8.)

[5] 郭丽.基于VLBI跟踪观测的空间飞行器瞬时状态参量归算[D].上海：中国科学院研究生院(上海天文台)，2007:26-37.(Guo Li. Reduction of the Instantaneous State Vectors of Spacecraft Based on VLBI Tracking Data [D]. Shanghai: Graduate University of the Chinese Academy of Sciences (Shanghai Astronomical Observatory), 2007:26-37.)

[6] 张捍卫，盘关松，马高峰.VLBI观测的电离层延迟改正模型研究[J].测绘学院学报，2003， 20(1): 14-18.(Zhang Hanwei, Pan Guansong, Ma Gaofeng. Research on the Ionosphere Delays Correction Model for VLBI Observation [J]. Journal of Institute of Surveying and Mapping, 2003, 20(1): 14-18.)

[7] R N Treuhaft，G E Lanyi.The Effect of the Dynamic Wet Troposphere on Radio Interferometric Measurements[J]. Radio Science， Vol.22，No.2，pp.251-265，1987.

[8] 张守余，阮仁桂，李晓杰，杜兰. CEI在GEO精密定轨中的应用及仿真计算[C].2007航天测控技术研讨会,2007：549-554.

[9] S W Thurman.Galileo Earth Approach Navigation Using Connected-Element Interferometer Phase-Delay Tracking[R]. TDA Progress Report 42-100，1990：34-47.

[10] C Edwards, Jr., D Rogstad, D Fort, L White, B Lijima. The Goldstone Real-time Connected Element Interferometer[R]. TDA Progress Report 42-110, pp.52-62, Aug. 15, 1992.

[11] David W Allan, Marc A Weiss. Accurate Time and Frequency Transfer During Common-view of a GPS Satellite[C]//Proceedings of the 34th Annual Frequency Control Symposium. Monmouth, WJ: IEEE, 1980:334-356.

[12] Dieter Kirchner. Two-way Time Transfer via Communication Satellites[J]. Proceedings of IEEE, 1991, 79(7):983-990.

[13] IMAE M. Review of Two-Way Satellite and Frequency Transfer[J]. Journal of Metrology Society of India, 2006, 21(4):243-248.

[14] 梁双有,任燕.利用光纤进行高精度时间传递[J]. 时间频率学报, 2003, 26(1):75-80.(Liang Shuangyou, Ren Yan. High-Precision Time Transfer via Optical Fibel [J]. Journal of Time and Frequency, 2003, 26(1):75-80.)

[15] 陈法喜,梁双有,赵侃,等.光纤时间传递延迟补偿实验进展[C].第二届中国卫星导航年会CSNC2011，2:679-686.

[16] 李孝峰,梁双有,张首刚.光纤时间频率传输数字相位补偿方法[J].时间频率学报, 2009, 32(2):115-119.(Li Xiaofeng, Liang Shuangyou, Zhang Shougang. A Method of Digital Phase Compensation for Time and Frequency Transfer via Fiber [J]. Journal of Time and Frequency, 2009, 32(2):115-119.)

[17] Kiman P W. Delta Differential One-way Ranging [R]. DSMS Telecommunications Link Design Handbook, 810-005, Rev.E, 2004.

[18] 唐歌实.深空测控无线电测量技术[M]. 北京: 国防工业出版社, 2012:118.(Tang Geshi. Radiometric Measuring Techniques for Deep Space Navigation [M]. Beijing: National Defense Industry Press, 2012:118.)

TheAnalysisofErrorSourcesofConnectedElementsInterferometry

LU Weitao YANG Wenge HONG Jiacai
The Academy of Equipment, Beijing 101416， China

AccordingtocharacteristicsofCEI,thesystemerrorsarethoroughlyanalyzedfirstly,includingclockerror,baselineerror,phaserippleerror,etc.Thenthechannelerrorscausedbyionosphereandtropospherearededucedbyusingfieldanglebetweenthetargetandbaselineasparameter.Finally,thebestanglemeasuringprecisionisobtainedbylimitanalysismethodandthenthebaselinelengthissuggested.Theclockerroristhemainerrorsourcewhenbaselineisshortandtheionosphereerroristhemainerrorsourcewhenbaselineisrelativelylonger.Basedoncomprehensiveconsiderationofmeasuringerrorandcost,thebaselinelengthsetataround10kmisproper.

CEI;Systemerror;Channelerror;Baselinelength

*总装武器试验技术重大项目(2011SY41A7001)

2014-03-11

路伟涛(1985-)，男，河南人，博士研究生，主要研究方向为航天测控、干涉测量技术；杨文革(1966-)，男，江西人，博士，教授，博士生导师，主要研究方向为航天测量与控制、雷达信号处理；洪家财(1967-)，男，安徽人，博士，副教授，硕士生导师，主要研究方向为航天测控技术，干涉测量技术等。

TN98

： A

1006-3242(2014)05-0071-06