爆破振动波形预测模型及应用★
徐芳妹 唐 健
(1.山东科技大学土木工程与建筑学院,山东 青岛 266590; 2.中国葛洲坝集团股份有限公司重庆分公司,重庆 401320)
爆破振动波形预测模型及应用★
徐芳妹1唐 健2
(1.山东科技大学土木工程与建筑学院,山东 青岛 266590; 2.中国葛洲坝集团股份有限公司重庆分公司,重庆 401320)
依据爆炸的几何相似原理,构造波形函数,建立了爆破振动时程波形预测模型,结合具体实例,对单段爆破和微差爆破的波形进行了预测,模拟出的波形基本符合地面振动波的传播规律,增加了爆破的安全性。
爆破振动,波形函数,振动波形,预测模型,预测波形
工程爆破在国民经济发展中发挥着至关重要的作用,在矿山、水利、交通等工程中得到广泛的应用。它加快了工程建设的进度,节约了能耗,但与此同时也带来了一些负面影响,包括爆破地面振动、爆破个别飞散物、冲击波等等。随着人们生活质量的提高和爆破环境的复杂化,对爆破效果的控制要求越来越严格,因此爆破灾害的预测与控制是岩土爆破界亟待解决的问题。
由于爆破振动涉及到的因素有很多方面,与炸药量、炮孔大小、地质条件、爆破环境等物理量都有关系。到目前为止,以往的爆破预测大都是建立在通过对大量测试数据进行回归和统计分析基础上得到的,以经验公式和经验系数为主,但也只能对爆破振动效应幅值的大小进行预测。现有的关于爆破振动强度预测的经验公式大都符合以下形式[1]:
V=kQmRn
(1)
其中,V为用来描述爆破振动强度的物理量,例如振动速度、加速度、位移等;Q为炸药量,kg;R为测点到爆源中心的距离,m;k,m,n均为与爆破条件、地质特性等相关的系数。
综合比较现在世界各国应用于爆破振动强度预测的经验公式,如中国的萨道夫斯基公式[2],美国矿务局的经验公式[3]等等基本都符合式(1)的形式,只是表达方式不尽相同,但其预测结果差别并不是很大。
经过大量的试验比对,专家学者们发现用爆破振动的峰值速度来描述爆破振动强度最有意义,从而延伸到对爆破振动波形的预测。这样不仅可以预测幅值大小,还能看出不同频率下相位的分布。吴从师[4]、徐全军[5]、刘军[6]、Yang[7]等都在波形预测上进行了深入研究,非常具有代表性。此外,近年来随着人工神经网络方法的出现,也有人把此方法应用于预测爆破振动强度[8,9],该方法有着极强的非线性动态处理能力,在爆破振动预测方面发挥着强有力的作用。
1 信号函数形式分析
1.1 应力波初始波形特点
P.J.Tidman和J.R.T.Grant通过下述实验[10]:炸药类型EN1509(密度1.6 g/cm3,爆速7 000 m/s),药量100 g,炮孔直径25 mm,装药方式选用条形耦合装药,在13%的孔四周贴绕长10 mm的带状铝箔(宽2 mm,厚5 μm)的传感器来监测孔壁运动。得出振动的主振周期1 μs,主振频率1 000 kHz,最大振幅1.6 mm/μs,主要震荡次数是1次。
另外,A.M.斯坦福尔得提出:一个长6.7 m的药卷在波速为6 167 m/s的岩石中以6 500 m/s的速度爆轰,应力波衰减指数n=1.44,圆频率ω=0.014 μs,则波的形状为:
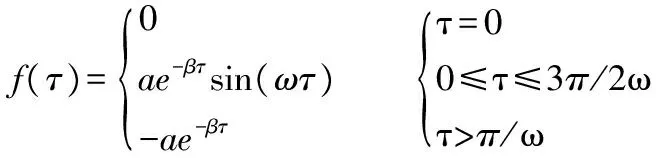
总结上述各个实验,发现在单孔爆破时,应力波波形在初始阶段基本相同。在短时间内,压力快速升高到很大,然后开始下降。波形在经历1个~2个周期后开始衰减,衰减速度由慢及快。此外,主振频率和峰值差别较大。
1.2 确定信号函数
信号函数只与爆炸的初始条件有关,其影响因素包含很多方面。在耦合装药条件下,设单孔信号函数为ajδ(t),其中,aj为第j个炮孔爆炸强度幅值;δ(t)为单位脉冲函数[11]。其中:
aj=bcj
(2)
cj=Qj/Q0
(3)
其中,aj的确定方法如下:首先确定一种标准炸药,然后寻找一个标准药量Q0能与a0=1对应。则b为实际使用的炸药波阻抗与标准炸药波阻抗的比值,Q为第j个炮孔的药量。
若设mj为第j个炮孔装药的不耦合影响系数,已知耦合度不仅对初始参数的峰值有影响,而且对脉冲周期的影响也不容忽视。但考虑到要建模型,在这里先忽视它对脉冲周期的影响。因此,在不耦合装药条件下,可求得单孔信号函数为mjajδ(t)。
2 响应函数构建
响应函数的构建涉及到爆破的方方面面,能反映出在爆破过程中包含的各个因素。目前仅仅由单孔信号函数还无法算出其响应函数s(t),而需要通过对试验数据进行回归分析得到,在近场的爆破地震效应中最具代表性的是R.L.Yang,P.Katsabanis和W.F.Bawden的实测记录,实验记录情况见文献[12]。文献给出这样的结论:频率越高,振动波的衰减越慢。而远场振动波的衰减规律是在一个周期或一个波长上的能量衰减是一个常数。
国内外有关由爆破响应函数预测出的波形的几率资料有很多,综合比较可以发现当离爆破地点较近时,爆破的振动频率都在1 000 Hz以上。单孔爆破获得的振动信号中包含了爆破振动的各种属性特征,利用实测的单个炮孔爆破振动波形来表征群组炮孔的爆破振动特点也是有依据的,但大多数都停留在理论分析阶段。由于爆破的复杂性,爆破预测存在着很大误差,还需要进一步分析研究,增加其可靠性。
因此,在单孔爆破条件下,考虑到爆炸相似定律,结合萨道夫斯基公式,构建的单孔爆破地震波响应函数为[13]:
(4)
其中,s(t)为介质质点的振动峰值速度,cm/s;β为品质因子,取为70;k,α分别为与爆破点至介质质点间的地质条件、岩石特性等有关的系数和衰减指数,其取值可按表1选取;其他符号意义同前。

表1 爆区不同岩性的k,α值
经分析,该模型的构建同时考虑了振幅和频率的衰减规律,也考虑了影响爆破地震波振幅、频率衰减的较多因素的作用,减小了爆破预测的误差,对爆破地震波的全过程进行了模拟,可以运用到实际工程中,有助于对爆破地震进行评估和对爆破参数进行优化。


3 应用实例
青岛地铁一期工程(3号线)02标处于城市建成区内,周边军用、民用设施众多,管线密布,特别是地铁下穿青岛市市南区德国建筑群。如何主动控制爆破振动、防止爆破地震效应的发生已成为工程施工中的重中之重。
现场爆破试验选在中山公园站1号风井,井深24 m,地下水位埋深9.2 m,矩形断面,兼做施工竖井。试验中所采用的单段炸药量分别为0.85 kg,1 kg,现场测点布设图如图1所示。
风井周围环境较为复杂,东侧有一座三层砖石结构的楼房,北侧有市政燃气管道通过。它的围岩属于燕山晚期花岗岩及花岗斑岩类型,质地比较坚硬,需采用爆破法开挖,运用台阶法浅孔微差控制爆破,楔形掏槽,选用2号岩石乳化炸药,防水性能较好。井壁四周则可以充分依据光面爆破控制技术,采用导爆索配合光爆小直径炸药。根据《爆破安全规程》,一般砖房的爆破振动安全标准如表2所示。

表2 爆破振动安全允许标准

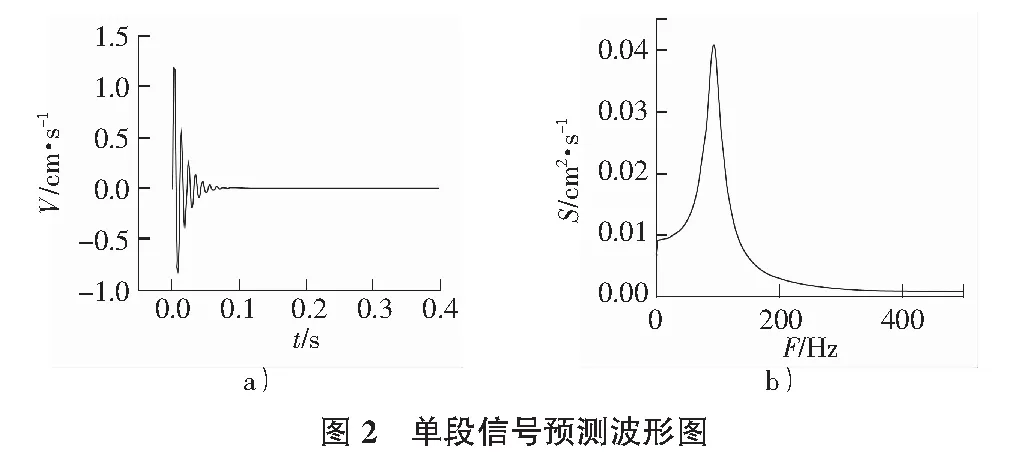
现场试验大体上可以分为两个部分,第一部分是进行单段爆破试验,第二部分是进行微差爆破试验。每个部分都要紧凑衔接,确保试验的准确性。为安全起见,首先进行爆破振动预测,依据构建的模型,单段爆破的预测波形如图2所示,包括时程曲线和频谱图。而实测的两个测点单段爆破的波形如图3所示。
通过图2和图3的对比,可以看出,预测波形与实测波形其特征基本相同,因此说明此模型满足实用要求。
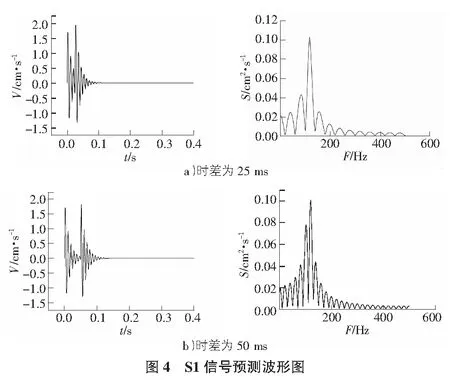
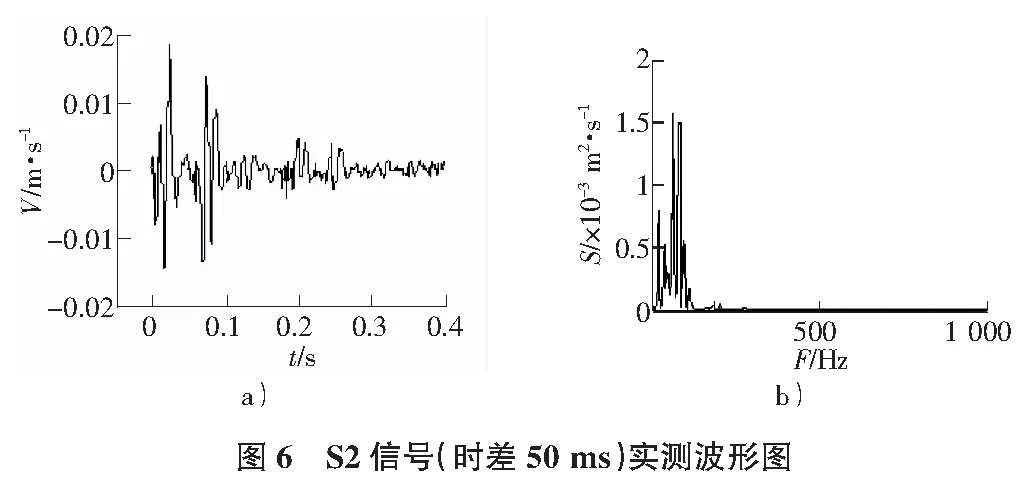
第二部分进行微差爆破试验,分为两步:1)在各段装药量不变的条件下,优先起爆第1段炸药,待微差时间t后再起爆第2段炸药,采集相应信号,编号为S1;2)在保证各段装药量及微差时间不变的前提下,起爆顺序与第一步正好相反,其他过程相同,采集到的信号编号为S2。考虑到雷管对微差时间的选取有限制作用,对间隔延期雷管爆破进行了合理的微差时间的预测,图4是微差时间分别为25 ms,50 ms爆破的预测波形结果。从图4可以看出,当微差时间为25 ms时,爆破振动的最大振幅为1.94 cm/s,主频为117 Hz;当微差时间为50 ms时,爆破振动的最大振幅为1.83 cm/s,主频为121 Hz。而单段爆破振动的最大振幅为1.85 cm/s,主频为116 Hz。亦即当微差时间为25 ms时,爆破振动强度增大,而当微差时间为50 ms时,两段信号独立且没有叠加,振动强度没有增大,说明微差时间为50 ms是合理的,这点也可通过试爆测试看出(见图5,图6)。
4 结语
本文通过运用爆破振动预测模型,分别对单段爆破和微差爆破的波形进行了预测,并且通过试验验证了模型的可靠性。由于在爆破中涉及的因素有很多,此模型较为全面的考虑了影响爆破振动的多因素作用,模拟出的波形基本能符合爆破地震波的传播衰减规律。不但能模拟出振幅的变化,而且可以模拟出频率的变化,为爆破设计提供更加充实的依据。
[1] 刘殿中,杨仕春.工程爆破实用手册[M].北京:冶金工业出版社,2004.
[2] 顾毅成,史雅语,金骥良.工程爆破安全[M].合肥:中国科学技术大学出版社,2009.
[3] Duvall W I,Petk of B.Spherical propagation of explosion of generated strain pulses in rocks [J].USBM, RI-5483,1959(15):21-25.
[4] 吴从师,吴其苏.爆破地震模拟初探[J].爆炸与冲击,1990,10(2):170-175.
[5] 徐全军,毛志远,张庆明.深孔微差爆破震动预报浅析[J].爆炸与冲击,1998,18(2):182-186.
[6] 刘 军,吴从师,高全臣.建筑结构对爆破震动的响应预测[J].爆炸与冲击,2002,20(4):333-337.
[7] Ruilin Yang,Tamara Whitaker.PPV man-gement and frequency shifting in soft ground near highwall to reduce blast damage[J].APS Blasts,2009(7):72-83.
[8] 吕淑然.爆破震动强度预测的神经网络模型研究[J].金属矿山,2009,396(6):40-42.
[9] 杨佑发,崔 波.爆破震动速度峰值的预测[J].振动与冲击,2009,28(10):195-198.
[10] P.J.Tidman, J.R.T.Grant.炮眼附近爆炸感应应力的实验研究[A].第二届爆破破岩国际会议论文集[C].1990:40-47.
[11] 林从谋.浅埋隧道掘进爆破振动特性、预报及控制技术研究[D].上海:同济大学,2005
[12] R. L.Yang,P.Rocque.通过测量振动和炮孔近场破坏状态研究爆破破坏[A].第四届国际岩石爆破破碎学术会议论文集[C].1995:139-147.
[13] [澳] D.P.布莱尔.爆破地震的测试、模拟和控制[A].第二届爆破破岩国际会议论文集[C].1990:62-76.
The prediction model and application of blasting vibration waveform★
XU Fang-mei1TANG Jian2
(1.CivilEngineeringandArchitectureCollege,ShandongUniversityofScienceandTechnology,Qingdao266590,China;2.ChinaGezhoubaGroupCompanyLimitedChongqingBranch,Chongqing401320,China)
Based on the geometric similarity principle, structure waveform function of explosion, this paper established the blasting vibration history waveform prediction model, combining with specific examples, predicted the waveform of single blasting and millisecond blasting, the simulated waveform basically meet the ground vibration wave propagation law, increased the blasting safety.
blasting vibration, wave function, vibration waveform, prediction model, prediction waveform
2014-07-16★:高等学校博士学科点专项科研基金(项目编号:20113718110002);爆炸冲击防灾减灾国家重点实验室开放课题(课题编号:DPMEIKF201307)
徐芳妹(1990- ),女,在读硕士; 唐 健(1989- ),男,助理工程师
1009-6825(2014)27-0035-03
TD235
A

