巨型框架悬挂减振结构的参数分析

宋丹丹 张涛涛 谈 荣

(1.东南大学土木工程学院，江苏南京 210096;2.南京智慧新城工程管理有限公司，江苏南京 210012)

高层悬挂结构体系可以分为核心筒体型和巨型框架型，均在国内外有典型的应用实例。核心筒体型的典型代表是，建于1970年的南非约翰内斯堡标准银行中心和建于1972年的德国慕尼黑宝马汽车行政大楼，还有建成较晚的德国哥廷根大学的XLAB试验大楼和上海浦东展览馆等;巨型框架型的典型代表是建于1985年的中国香港汇丰银行大厦，这些建筑均因其体量大、艺术效果好而被称为当地的标志性建筑，本文所做的研究就是基于这类悬挂结构的。巨型框架悬挂减振结构具有良好的抗震、抗风性能，建筑布局多变，功能适应性强，能够较好的应用于现代高层建筑的设计与使用中。文献［1］通过对一巨型框架悬挂结构进行数值模拟分析及试验研究指出，巨型框架悬挂减振结构由于阻尼装置的存在，结构的地震响应显著减小。本文将在文献［1］的基础上，研究巨型框架悬挂减振结构中阻尼器的参数对结构地震响应的影响。

1 数值分析模型

本文的主要目的是研究巨型框架悬挂减振结构中阻尼器的参数对结构地震响应的影响，选用的文献［1］中的原型结构作为分析模型，其基本概况在文献［1］中有详细阐述，在此不再一一赘述。

有限元分析软件ABAQUS以其强大的有限元分析功能和CAE功能，被广泛应用于土木工程、水利水工和机械制造等行业［2］，ABAQUS能够求解各种复杂的模型并能解决实际工程问题，在分析能力和可靠性等方面表现很好。本文即采用ABAQUS作为分析软件，为保证分析结果的可靠性，单元的选择和模型的准确建立是关键。本文即将建立的巨型框架悬挂减振结构有限元模型中，选用的单元类型为:S4R，B31，Springs/Dashpots，Connector。其中，S4R用于模拟巨型框架柱及巨型框架梁中的剪力墙及楼板、悬挂楼盖;B31用于模拟吊索及主结构和次结构所有的梁、柱;Springs/Dashpots用于模拟连接悬挂楼层与主体结构的粘弹性阻尼器;悬挂楼段与主结构中巨型框架梁的连接采用刚接，采用连接单元Connectors中Join+Align属性模拟，单元的相关介绍见文献［2］。由此建立的悬挂减振模型如图1所示。巨型框架和悬挂楼盖选用C50强度等级混凝土，弹性模量为3.45×1010N/m2，泊松比v=0.2，密度为2 550 kg/m3，材料阻尼采用瑞雷阻尼;悬挂次结构中吊索为CFRP筋材，弹性模量为1.8×1011N/m2，泊松比v=0.3，密度为 1 600 kg/m3。

2 参数设置及目标函数

以设置在悬挂楼层与巨型框架之间的阻尼器的阻尼系数c和刚度系数k作为本文进行参数分析的对象，阻尼器在结构中的位置和布置与文献［1］所述相同，且在参数分析过程中，各悬挂楼层处阻尼系数和刚度系数值同时变化且始终保持一致。巨型框架悬挂建筑结构最突出的优点即是其能够显著减小主结构的地震响应，本文进行参数分析的目的就是通过变化阻尼系数c或刚度系数k使得主结构的地震响应最小。

在巨型框架悬挂减振结构中，悬挂楼层作为主要的使用场所，其地震响应也应引起关注，如加速度响应值不能超过一定限值，否则将会引起人们使用过程中的不适，悬挂楼层的层间位移不能超过一定限值，否则将会引起非结构构件的破坏，而在地震作用下悬挂楼层中非结构构件的损坏程度直接影响到震后的修复费用，而以往的研究主要针对主体结构—巨型框架的地震响应的无约束优化，而忽略悬挂楼层的层间位移响应，导致优化的结果有着片面性。根据GB 50011-2010建筑抗震设计规范有关层间位移角限值的规定，罕遇地震作用下，层间位移角限值为1/550≤［θ］≤1/50时比较适合，其具体定值与悬挂楼面内非结构构件的变形能力相关［3］，设计中须考虑其对优化结果的影响。

通过上述的分析可给出本文多目标优化控制的方程如下:

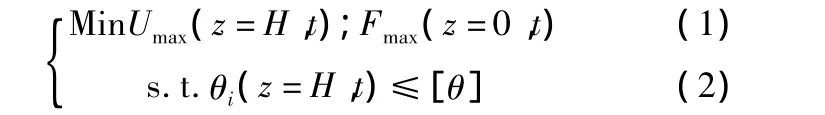
式(1)给出了地震响应参数分析的优化目标是寻找参数c和k，使得主体结构—巨型框架结构顶点位移响应时程的峰值Umax和结构底部剪力时程响应的峰值Fmax为最小，其中，H为巨型框架总高度;式(2)给出了进行参数分析的约束条件——悬挂楼层的层间位移角响应最大值θi，其中［θ］为层间位移角响应限值，它与结构控制的目标有关。为了将目标函数化为无量纲函数，可引入两个新的目标函数:

式(3)和式(4)中给出了巨型框架顶点位移和结构底部剪力的无量纲目标优化函数，ΔU和ΔF为巨型框架顶点位移和底部剪力的减振系数，可见ΔU和ΔF越大，减振效果越好;其中，U0和F0分别为响应地震波输入下刚性杆模型的主结构—巨型框架顶点位移响应时程峰值和结构底部剪力响应时程峰值。

同时考虑式(3)和式(4)时会为参数优化带来不便，因此可考虑创建新的目标函数，将两者合并，即取式(3)和式(4)中两个函数的线性组合作为新的目标函数，即可得:

其中，Δ为综合减振系数。

3 阻尼系数优化结果及分析

选取EI Centro波和Taft波前16 s的加速度时程记录，按规定的地震波的调整方法，将加速度时程曲线峰值调整为4 m/s2，作为输入地震波，利用有限元软件ABAQUS进行地震响应时程分析，并由此得到结构底部剪力响应、主结构顶点的位移响应和悬挂楼层的位移响应。图2给出了加速度峰值为4 m/s2的EI Centro波和Taft波输入下，刚度系数一定时，主结构—巨型框架的综合减振系数Δ和悬挂楼层的层间位移角响应的最大值随阻尼器阻尼系数c的变化曲线。由图2综合减振系数Δ的变化曲线可看出:

1)在巨型框架悬挂减振模型中，当固定阻尼器的刚度系数保持不变时，结构的综合减振系数Δ的值与阻尼器的阻尼系数有关，随阻尼系数的增大，综合减振系数先缓慢增大后急剧减小，在k=106N/m时，有极大值，说明当阻尼器的刚度系数一定时，阻尼系数存在最优值使得减振系数取得最大值，即取得最优的减振效果;

2)当阻尼器的阻尼系数相同时，综合减振系数Δ的值与刚度系数有关，刚度系数k=106N/m下巨型框架悬挂减振结构的减振效果要略差于阻尼器刚度系数为0时的减振效果;

3)在阻尼系数值较小时，悬挂楼层层间位移角的最大值变化较小，在c=103N·s/m～107N·s/m之间变化比较剧烈，随后基本保持不变;考虑减小主结构的地震响应的同时，还应考虑悬挂楼层的地震响应，控制悬挂楼层层间位移角在允许值内，当阻尼器的阻尼系数位于最优值附近时，不仅综合减振系数取得极大值，而且层间位移角也能得到有效控制;

图2 减振系数和悬挂楼层最大层间位移角随阻尼系数的变化曲线

4)对比图2a)和图2b)中综合减振系数Δ的变化曲线可以看出，输入地震波不同，综合减振系数值不同，但随阻尼系数变化而改变的趋势相同，刚度系数相同时，阻尼系数的最优值也相同;对比图2a)和图2b)中层间位移角最大值的变化曲线可以看出，输入地震波不同，层间位移角最大值的变化趋势相同，且在刚度系数和阻尼系数相同时，相差不大。

4 刚度系数优化结果及分析

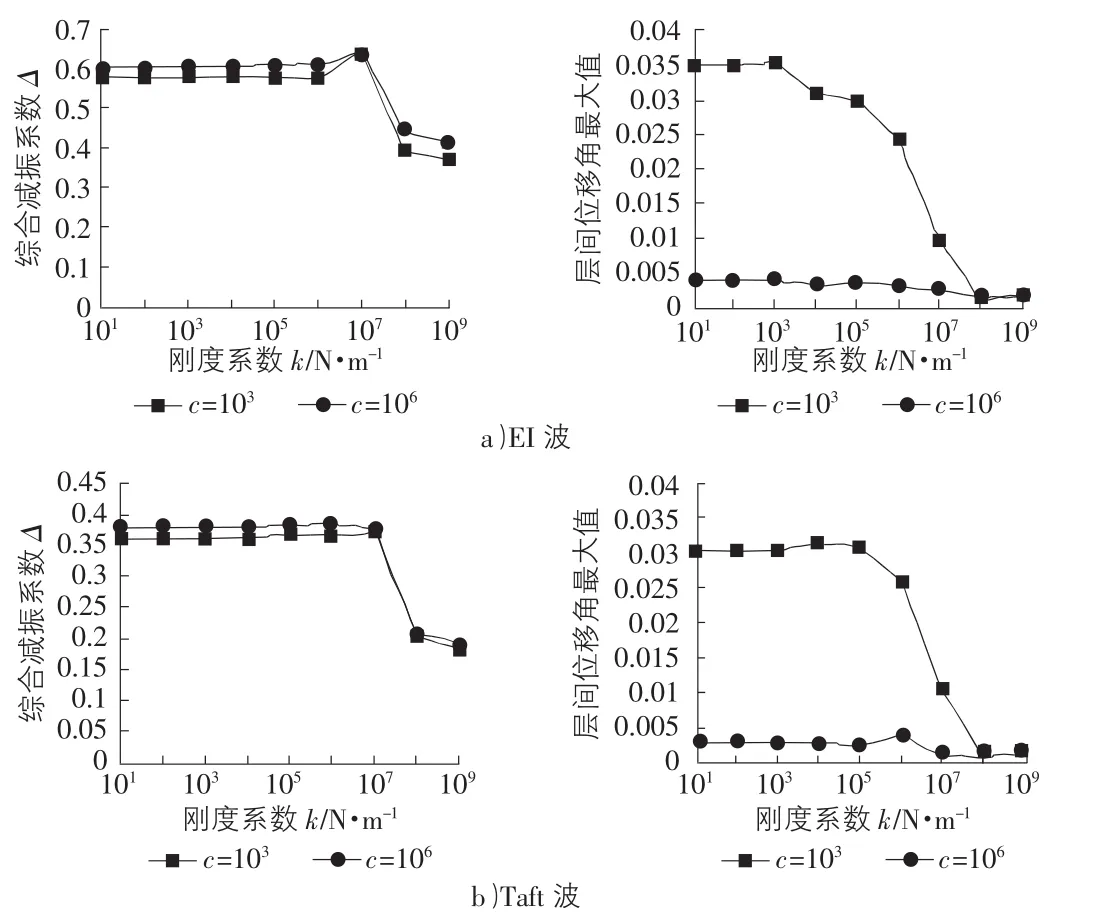
图3 减振系数和悬挂楼层最大层间位移角随刚度系数的变化曲线

图3给出了加速度峰值为4 m/s2的EI Centro波和Taft波输入下，阻尼系数一定时，主结构—巨型框架的综合减振系数Δ和悬挂楼层的层间位移角响应的最大值随阻尼器的刚度系数k的变化曲线。从图3中可以看出，当固定阻尼器的阻尼系数恒定时，结构的综合减振系数Δ的值随刚度系数的增大先缓慢增大后急剧减小，当刚度系数小于105N/m时，阻尼器的刚度对综合减振系数的影响较小，因此当所选择的阻尼器的类型确定时，若其刚度较小，则可不考虑阻尼器刚度对主结构动力响应的影响;存在最优刚度系数，约为106N/m～107N/m时，使得综合减振系数最小;阻尼器阻尼系数不同，综合减振系数值相差不大;对比图3a)和图3b)，综合减振系数的值随输入地震波的不同差异较大，但变化趋势相同。从图3中层间位移角随刚度系数的变化曲线可以看出，随着阻尼器刚度的增大，层间位移角最大值响应先略微增大后迅速减小，阻尼系数不同，层间位移角最大值随刚度系数的变化的差异较大，阻尼系数取最优值时，层间位移角响应最大值较小，且当刚度系数变化时，均处于位移角限值内，因此，当阻尼器刚度一定时，可以通过提高阻尼器的阻尼系数来控制悬挂楼层的层间位移角;对比图3a)和图3b)可得，输入地震波不同，层间位移角最大值变化趋势相同。

5 阻尼器的选择

巨型框架悬挂结构体系为高层建筑结构体系的一种，因其具有较好的建筑艺术效果而非常适用于商业建筑，设计中，对其侧移和舒适度的要求较为严格;且在控制巨型框架侧移的同时，还需保证悬挂楼层的位移满足要求。通过本文的分析可知，要使主体结构的减振系数达到最优，且悬挂楼层的位移能得到有效控制，阻尼器须同时具有阻尼和刚度两项参数，即阻尼器在增加结构阻尼的同时也需要增加结构的侧向刚度。因此，可以选择粘弹性阻尼器或者金属屈服耗能装置。

6 结语

1)建立了数值分析模型并设定了目标函数，为后续研究阻尼器的阻尼系数和刚度系数的变化对结构地震响应的影响奠定了基础;2)通过保持刚度系数不变，分析阻尼系数对结构地震响应的影响可知，存在最优的阻尼器的阻尼系数使综合减振系数最大，此时悬挂楼层的位移角也能得到有效控制，既满足规范规定的限值要求，且可以通过增加刚度系数来减小层间位移角;3)通过保持阻尼系数不变，分析刚度系数对结构地震响应的影响可知，存在最优的刚度系数使综合减振系数最大，而此时悬挂楼层层间位移角可能不满足要求，这可以通过增加阻尼系数来保证。

［1］张 伟.新型巨型框架悬挂减振结构体系理论分析与试验研究［D］.南京:东南大学，2011.

［2］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京:机械工业出版社，2007.

［3］王春林，吕志涛，吴 京.高层核心筒悬挂结构地震响应的参数分析［J］.工程抗震与加固改造，2008，30(1):60-63.