基于改进模糊层次分析法的地铁车站施工风险评价

邓沿生 梁士举

(1.上海同是工程科技有限公司，上海 200001;2.洛阳师范学院，河南 洛阳 471000)

0 引言

随着城市地铁建设的迅速发展，地铁施工引起的工程事故也越来越多，一旦工程事故发生，往往会造成巨大的经济损失和人员伤亡。由于地铁车站工程具有技术复杂、不可预见风险因素多和社会影响大等特点，对其进行风险评价研究具有重要意义。

目前，对深基坑工程和地铁盾构隧道施工风险分析的研究较多。周红波提出基于贝叶斯网络的深基坑风险模糊综合评估方法［1］;张驰、黄广龙等基于模糊数学的相关理论实现深基坑施工对周边环境影响的模糊风险评估［2］;周红波、姚浩等采用WBS方法对上海某轨道交通深基坑工程工作结构进行分解，采用故障树法对风险事件以及风险因素进行识别，应用综合集成风险评估方法进行风险评估［3］;周红波、何锡兴等将分解分析法和故障树法结合使用，对地铁盾构隧道施工进行风险分析［4］;刘凌云、杨德磊等采用层次分析法对隧道盾构进出洞进行风险分析［5］;陈自海、陈建军等采用模糊层次分析法对盾构隧道施工进行风险分析［6］。鲍学英、王起才等根据《地铁施工安全评价标准》，从施工安全组织管理评价、施工环境安全管理评价、施工安全监控预警管理评价以及施工安全技术管理评价4个方面对地铁施工安全风险进行评价［7］。由此可以看出，对地铁车站施工进行的风险分析相对较少。

本文针对地铁车站施工进行风险识别，结合GB 50652-2011城市轨道交通地下工程建设风险管理规范［8］提出的工程建设风险等级标准，采用改进模糊层次分析法(FAHP)［9-11］进行风险评价，更加符合人类思维判断的一致性，且不需进行判断矩阵的一致性检验，简化计算过程。此外，通过改换计算因素权值的公式，提高评价因素间相对重要程度的分辨率，最后对评价结果进行有效性验证，为类似工程建设提供参考。

1 FAHP风险评价步骤

1.1 建立风险因素层次模型

根据地铁车站工程地质特点和周围建筑物情况对风险事件和风险因素进行识别，建立风险因素层次模型，形成中间因素集U和相对应的指标因素集ui:

1.2 确定风险因素发生可能性和损失等级

根据文献［7］中给出的风险发生可能性等级标准和风险损失等级标准对指标因素集ui中各因素风险发生可能性(P)和损失(C)均划分为5个等级进行估值，如表1和表2所示。

表1 风险发生可能性等级标准

表2 风险损失等级标准

由各指标因素的风险值R=P×C，建立指标因素集ui的风险值集Ri:

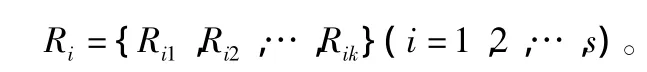
1.3 构建优先关系判断矩阵

为了准确描述任意两个风险因素的相对重要程度，采用表3所示0.1～0.9数量标度建立中间因素相对于总目标的优先关系判断矩阵A和指标因素相对于中间因素的优先关系判断矩阵M:

表3 0.1 ～0.9 数量标度

1.4 构建模糊一致矩阵

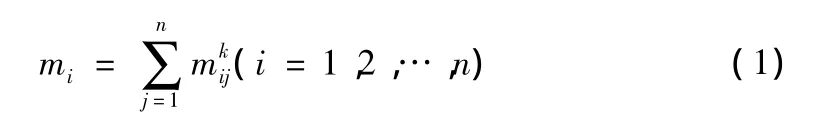
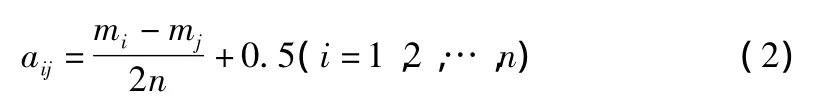
1.5 确定风险因素权重

根据式(3)计算目标层下各中间因素的权重B以及中间因素层下相对应的各指标因素的权重wi:

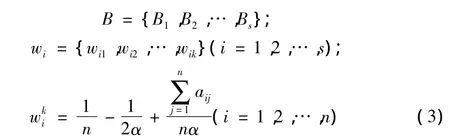
其中，参数α满足α≥(n－1)/2。

1.6 构造隶属函数

根据文献［7］，工程建设风险等级标准宜分为四级，结合估值按梯形构造隶属函数［2］。

Ⅰ级:

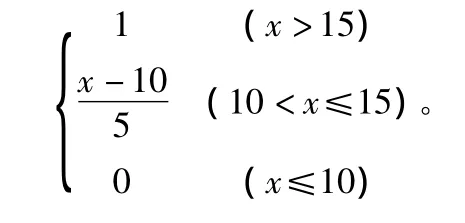
Ⅱ级:

Ⅲ级:

Ⅳ级:

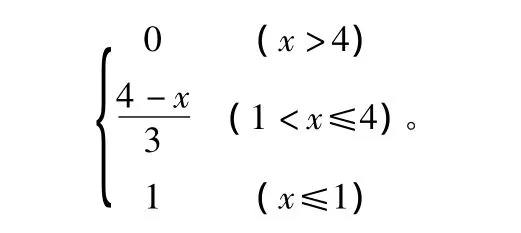
1.7 确定风险等级

求中间因素层的评价向量Fi:

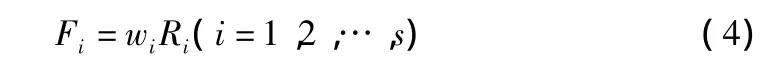
总目标评价向量Z:

将总目标风险值代入隶属函数，得到隶属向量，根据最大隶属度原则，得到总目标的风险等级。

由于根据最大隶属度原则确定总目标风险等级可能造成部分信息丢失，甚至得出不合理的结论。因此，应根据式(6)对最终的风险等级进行有效性验证［12］。

式中:α——有效指数;

β，γ——隶属向量中最大分量和次大分量占各分量总和的比例;

m——风险评价等级总等级的数目。

α值对应的有效性区间为:

当α=0时，隶属度原则完全无效;当α∈(0，0.5)时，隶属度原则低效;当 α∈［0.5，1)时，隶属度原则比较有效;当 α∈(1，+∞)时，隶属度原则非常有效;当α=+∞时，隶属度原则则完全有效。

2 实例分析

某地铁车站沿城市主干道南北向布置，为地下2层岛式车站，基坑长255 m，宽 19.2 m，开挖深度约15.1 m ～21.8 m。围护结构采用800 mm厚地下连续墙+内支撑支护，其中，第一道为钢筋混凝土支撑，其余均为钢支撑。该车站基坑工程安全等级为一级，基坑保护等级为一级。基坑开挖所涉及地层上部主要为杂填土和淤泥;中部主要为粉(砂)质土;下部主要为残积土和全风化岩。

2.1 建立风险因素层次模型并估值

根据地铁车站工程概况、地质、水文和周边环境，建立风险因素层次模型，并组织专家根据表1和表2对各指标因素进行估值，如表4所示。

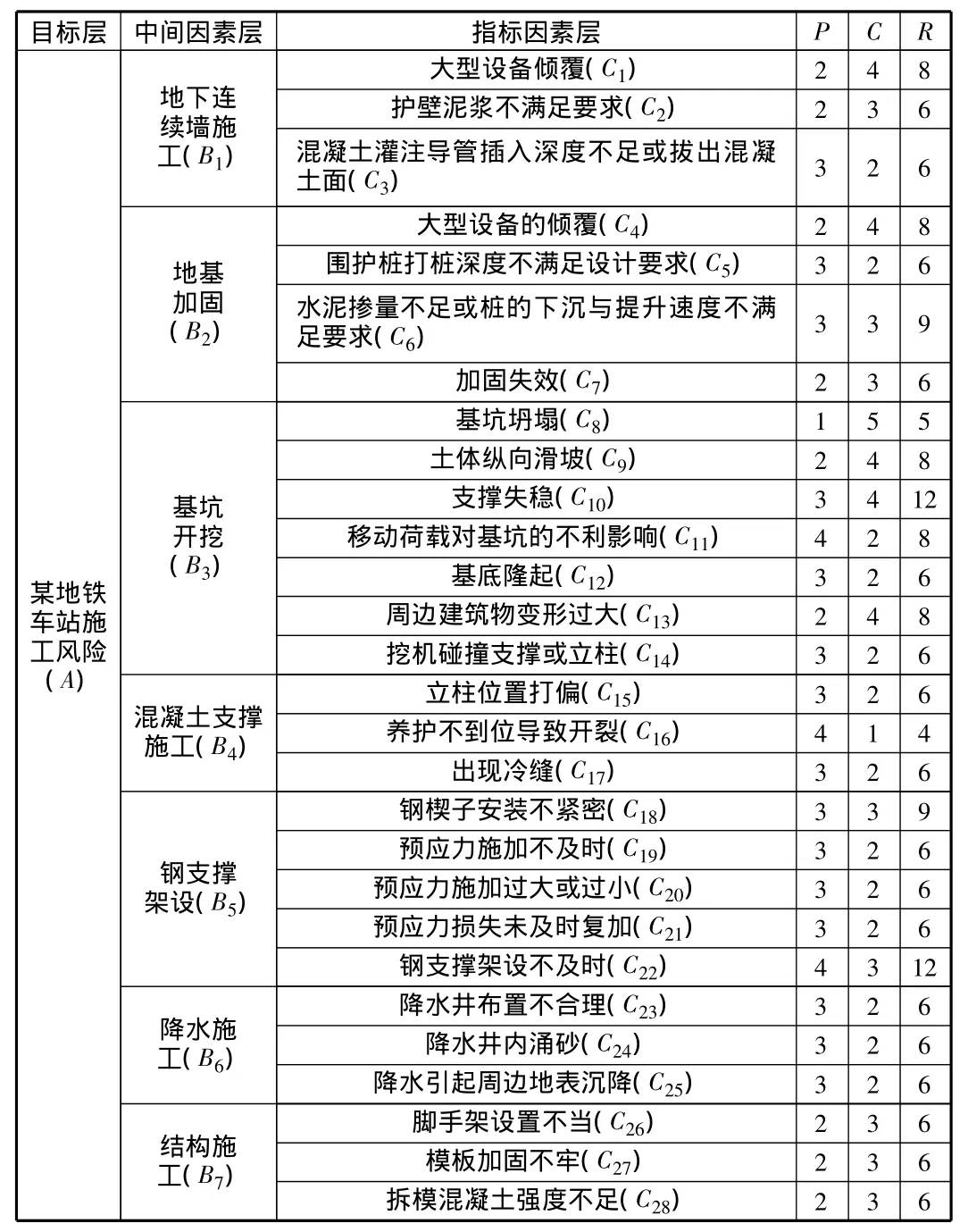
表4 风险因素层次模型及指标因素估值

2.2 构建优先关系判断矩阵并计算权重

根据表4风险因素层次模型结合表3构建中间因素相对于总目标的优先关系判断矩阵A:

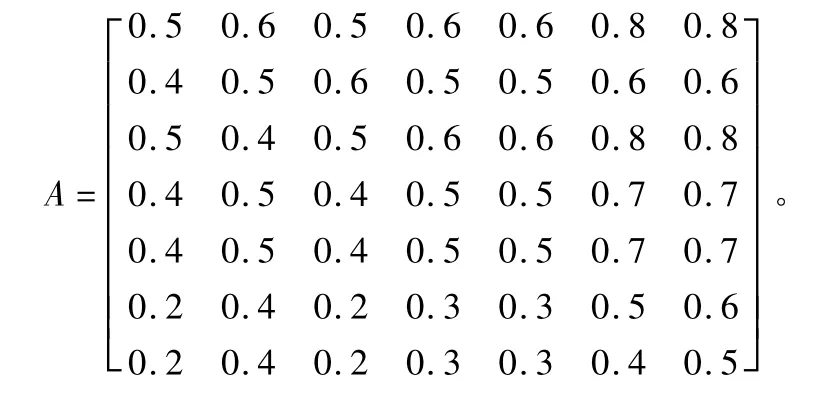
指标因素相对于中间因素的优先关系判断矩阵M:

根据式(1)和式(2)把优先关系矩阵转换为模糊一致矩阵，再根据式(3)计算目标层下各中间因素的权重向量B:

中间因素层下相对应的各指标因素的权重向量wi:

将权值归一即可得到风险因素C1～C28相对总目标的综合权重向量为:

(0.065 7，0.046 5，0.052 0，0.034 4，0.038 1，0.029 5，0.045 5，0.029 6，0.024 3，0.025 4，0.018 2，0.018 6，0.025 1，0.018 2，0.054 1，0.045 2，0.049 2，0.032 5，0.028 0，0.024 4，0.025 1，0.037 6，0.039 7，0.033 7，0.045 6，0.047 6，0.038 1，0.028 6)。

2.3 确定风险等级

根据式(4)和式(5)，得出该地铁车站施工风险值为6.791 3，代入隶属函数，得到隶属向量为:(0，0.465 2，0.534 8，0)。根据最大隶属度原则，该地铁车站施工风险应为Ⅲ级，属于可接受的风险。

将隶属向量代入式(6)进行结果有效性验证，求得有效指数α=0.408＜0.5，所以隶属度原则低效。结合隶属向量可以得出，虽然该地铁车站施工风险为Ⅲ级，但接近Ⅱ级，属于Ⅲ级中风险偏上的水平，应加强日常管理与监测。

3 结语

根据地铁施工特点对风险进行识别，采用改进模糊层次分析法建立风险因素层次模型并进行风险评价，得出以下结论:

1)建立的风险因素层次模型结构合理，清晰易懂，改进模糊层次分析法更加符合人类思维判断的一致性，可以减少主观因素对评价结果的影响。模糊一致判断矩阵无需进行一致性检验，简化了计算过程。

2)采用改进模糊层次分析法得出该地铁车站施工风险等级为Ⅲ级，属于可接受的风险。通过最大隶属度原则有效性验证发现评价结果为低效，最后对隶属向量进行分析表明:该地铁车站施工风险等级属于Ⅲ级中风险偏上的水平，决策者应予以关注。

［1］ 周红波.基于贝叶斯网络的深基坑风险模糊综合评估方法［J］.上海交通大学学报，2009，43(9):1473-1479.

［2］ 张 驰，黄广龙，李 娟.深基坑施工环境影响的模糊风险分析［J］.岩石力学与工程学报，2013，32(S1):2669-2675.

［3］ 周红波，姚 浩，卢剑华.上海某轨道交通深基坑工程施工风险评估［J］.岩土工程学报，2006，28(sup):1902-1906.

［4］ 周红波，何锡兴，蒋建军，等.地铁盾构法隧道工程建设风险识别与应对［J］.地下空间与工程学报，2006，2(3):475-479.

［5］ 刘凌云，杨德磊，郭海柱.隧道盾构进出洞施工风险分析［J］.低温建筑技术，2010(8):51-53.

［6］ 陈自海，陈建军，杨建辉.基于模糊层次分析法的盾构隧道施工风险分析［J］.地下空间与工程学报，2013，9(6):1427-1432.

［7］ 鲍学英，王起才，宫文昌.基于模糊层次分析法的地铁工程施工安全评价［J］.中国安全生产科学技术，2013，9(1):136-139.

［8］ GB 50652-2011，城市轨道交通地下工程建设风险管理规范［S］.

［9］ 张吉军.模糊层次分析法(FAHP)［J］.模糊系统与数学，2000，14(2):80-88.

［10］ 陶余会.如何构造模糊层次分析法中模糊一致判断矩阵［J］.四川师范学院学报(自然科学版)，2002，23(3):282-285.

［11］ 张吉军.模糊一致判断矩阵3种排序方法的比较研究［J］.系统工程与电子技术，2003，25(11):1370-1372.

［12］ 韩 利，梅 强，陆玉梅，等.AHP——模糊综合评价方法的分析与研究［J］.中国安全科学学报，2004，14(7):86-89.