基于遗传算法的钴结壳采矿车行走路径规划研究

陈 波(长沙航空职业技术学院,湖南 长沙 410124)

基于遗传算法的钴结壳采矿车行走路径规划研究

陈 波
(长沙航空职业技术学院,湖南 长沙 410124)

海洋富钴结壳是海洋矿产资源中经济价值高又极具战略意义的矿产之一。富钴结壳主要位于海洋的海山表面，因所处地形地貌复杂多样，所以开采难度非常大。基于遗传算法对钴结壳采矿系统中关键的采矿车行走路径问题进行了研究。

钴结壳采矿车；路径规划；遗传算法

矿产资源是人类社会进步和经济发展的物质基础。从长远来看，矿业在国民经济和社会发展中基础地位不可替代。在世界经济和科学技术高速发展的今天，各国政府已逐渐将目光从内陆投向资源丰富的海洋，而富含多种稀缺矿物的海底多金属结壳开发也成为各国大力发展的战略目标。海洋富钴结壳(铁锰结壳、锰结壳)是现今所探索到的最具战略发展意义和潜在经济价值的海洋矿产资源之一，矿体富含钴、钛、铈、铂和镍等多种稀贵金属，其中钴的含量相比于陆地原生钴矿中钴含量净高几十倍，平均含量达到1%以上[1，2]。而据科学考察，仅太平洋某火山隆起地带就蕴含约为10亿吨的富钴结壳矿床[3，4]。但是，因富钴结壳多位于海洋山体斜坡表面处，开采环境恶劣复杂，结壳开采难度大。而研制一种能够在深海水域自主作业的移动车辆是深海采矿作业最关键的问题。钴结壳采矿车是深海采矿作业的主体，能够实现在水下自主作业功能，对其研究涉及众多学科领域[5]，其中采矿车路径规划是其研究的基础和重点[6]。

路径规划是钴结壳采矿车行走的关键步骤。钴结壳采矿车的行走是指采矿车在既定的海底采矿区域根据预先设定的路径进行安全行驶，并在行驶过程中高效地完成采矿作业。采矿车在海底的行走主要包括路径规划和路径跟踪两个部分。采矿车路径规划包括两个方面：1)高效地获得作业环境信息；2)在此基础上，规划采矿车的最优行走路径[7]。由于采矿车深海作业环境的极端复杂，作业要求具有多样性，因此采矿车的行走具有多约束性和多目标性[8]。

遗传算法(Genetic Algorithm)属于进化算法(Evolutionary Algorithms) 的一种，最初由美国Michigan大学J.Holland教授于1975年首先提出来，通过模仿自然选择和遗传机理获得最优解[9]。遗传算法主要包括三个算子：选择、交叉和变异[10]。本文以铰接式深海钴结壳采矿车为研究对象，在分析总体方案和主要控制执行元件的基础上，运用遗传算法研究其海底采矿作业行走路径。

1 采矿车路径规划总体方案设计

采矿车通过声纳传感器检测前方障碍物的信息。在行进过程中声纳传感器只能检测到障碍物面向采矿车这一侧的信息，而障碍物的完整信息却无法有效获取。为获取障碍物更多的有效信息，可以采用多次局部规划过程代替一次性规划，并在每次局部规划中充分利用该时刻最新的局部环境信息的方案。但是这种方案会导致控制系统实效性伴随频繁的局部路径规划操作而降低[11]。

本文采用障碍物膨胀处理的方法，提高控制系统算法效率，解决频繁局部路径规划的弊病，如图1所示，L1，L2是两条声纳线，点A，B分别是声纳探测线与障碍物的切点。假设障碍物的位置、尺寸正好位于以A，B两点为轴线的A、B劣弧后方之内。那么采矿车则可以直接沿着以劣弧A、B的镜像曲线为依据规划的路径行走，并逐步获取障碍物的完整信息。 如果A、B劣弧后方障碍物的位置、尺寸并不完全在A、B劣弧镜像曲线的范围内，则以当前障碍物的实际范围为依据，重新规划路径。

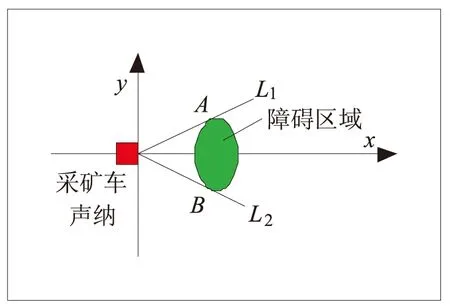
图1 采矿车声纳探测示意图

以上路径规划步骤如图2所示。

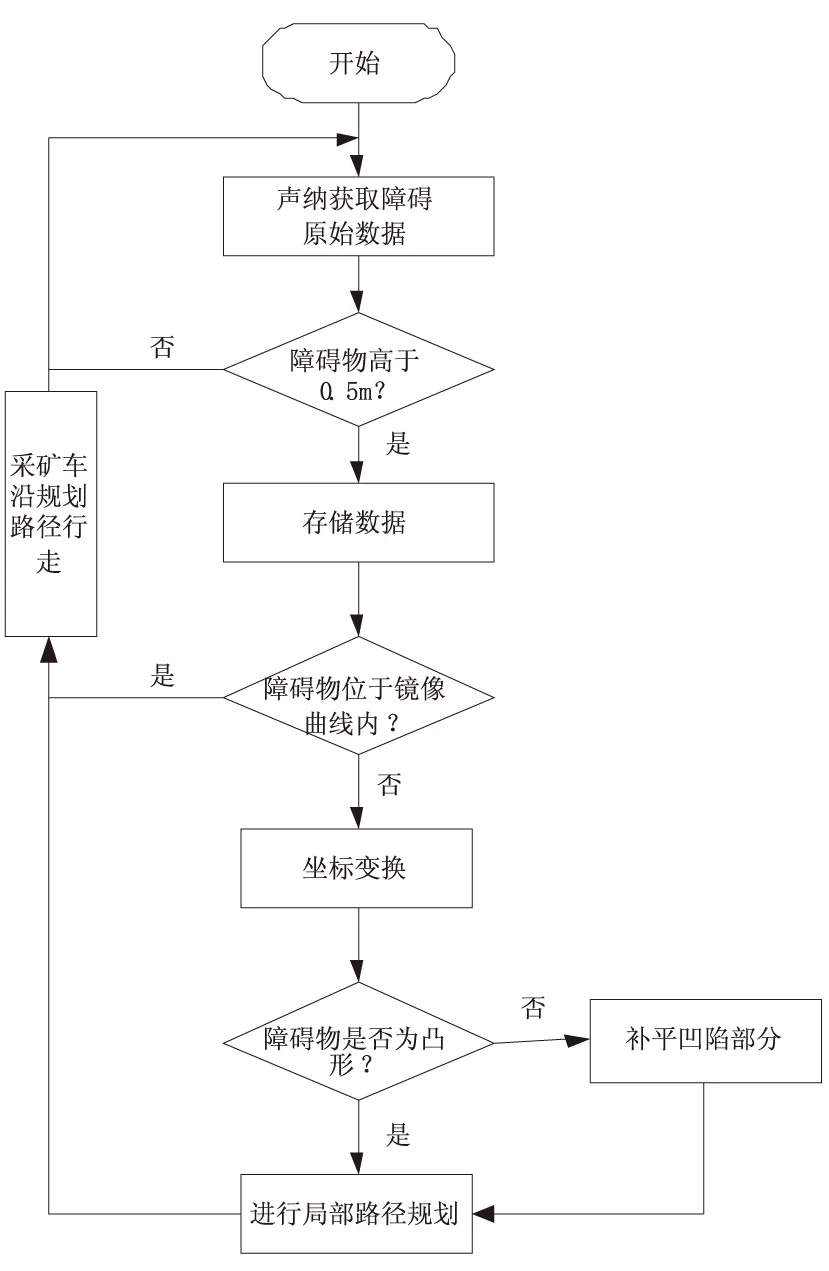
图2 路径规划流程图

2 基于遗传算法的采矿车路径规划

2.1 遗传算法的运算过程和设计

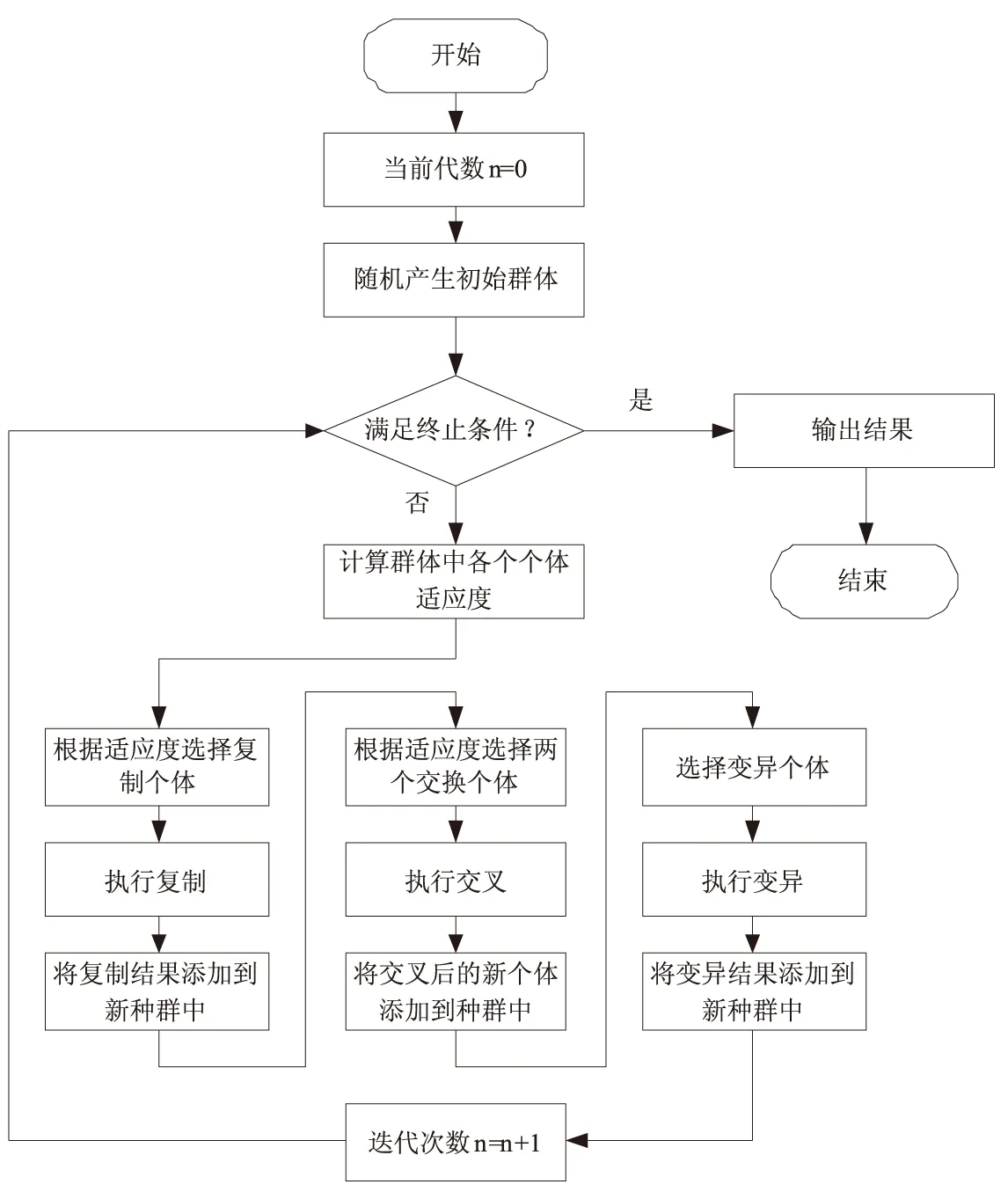
遗传算法属于进化算法的一种，其具体步骤如图3所示。

图3 遗传算法流程图

2.2 路径编码方式

遗传算法是在编码空间和解码空间中交替工作。所以解决路径编码问题[12]是基于遗传算法的路径规划研究的首要问题。

实际路径点都是二维的，为了提高算法的运算速度，需将二维路径坐标点进行降维处理。设当前坐标系为x0y，x轴为起始点与目标点的连线，起始点即为原点。将终点和起点间的线段等分为n段，取等分点xj(j=1，2，…，n-2)，设过xj点与x轴垂直的直线为Lj，在Lj上随机选取一点Pj，共得到n-2个点，P0，P(n-1)分别为起点、终点，如图4所示。

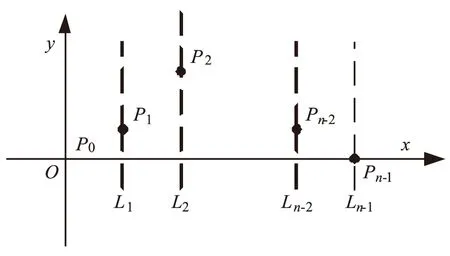
图4 路径编码示意图

路径规划等分点的间距应该保持在适当的范围内。根据采矿车的具体情况，把等分点间距定为1米。此外，局部规划路径的长度很大程度上由声纳探测器的作用距离决定。国产高端声纳探测器最大的作用距离为200米[13]，可以将路径规划最优检测长度设定为100米。在100米的路径区域里选取101个等分点(含首尾两点)，然后用随机数在每一个等分点生成相对应的纵坐标，依次连接所有的随机生成的点，得到一条随机路径。

等分点的纵坐标设为yi,j，随机路径为Ri，二维的实际路径通过以上步骤转化为一维的y坐标编码，采用浮点数方式编码，具体编码如下：

yi,0yi,1yi,2…yi,n-2yi,n-1

当采矿车的当前位置纵坐标为yi,0，目标点纵坐标为yi,n-1，路径则为：

Ri=((xi,0，yi,0)，(xi,1，yi,1)，…，(xi,n-1，yi,n-1))

(1)

对应的染色体为：

vi=(yi,0，yi,1，…，yi,n-1)

(2)

2.3 路径基因初始种群设定

由遗传算法获取的采矿车最佳行走路径是必须位于障碍物区域之外。但是从遗传学的角度来说，障碍物区域内靠近设定路径的点显然比平坦区域遥远的点更具有基因遗传的优越性。为了提高遗传基因的优势性，采用惩罚策略把具有遗传优势的点包含在初始群体的设定范围内，并对不可行解给予一定程度的罚分，使其适应值相应降低。

根据采矿车的具体作业情况，可将作业区域区分为两种：即障碍物区域和平坦区域。如图5所示，最优路径点出现在平坦区与障碍物区的交界处a点附近。在障碍物区的路径点c与最优路径点a的距离比平坦区中的路径点b近得多，虽然点c为不可行解，但是c点显然比b点更具有优势遗传基因信息。为了最大限度利用c点的优势遗传基因信息，允许它继续参与遗传运算，同时给予适当的惩罚，作为其违反路径安全性的一个判值。这样基于遗传算法的路径种群具备了从平坦区和障碍物区同时逼近最优解的优势。

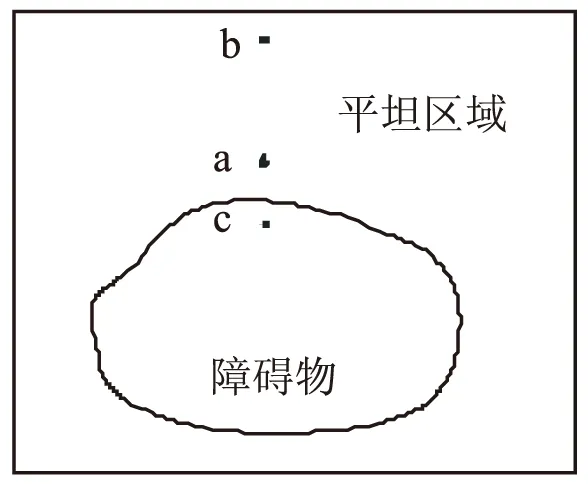
图5 平坦区域和障碍物区域示意图

采用惩罚策略可使初始种群随机点的搜索范围扩大到整个搜索空间。本文采用10条染色体，对应的初始随机路径布满整个采矿区域，如图6所示。

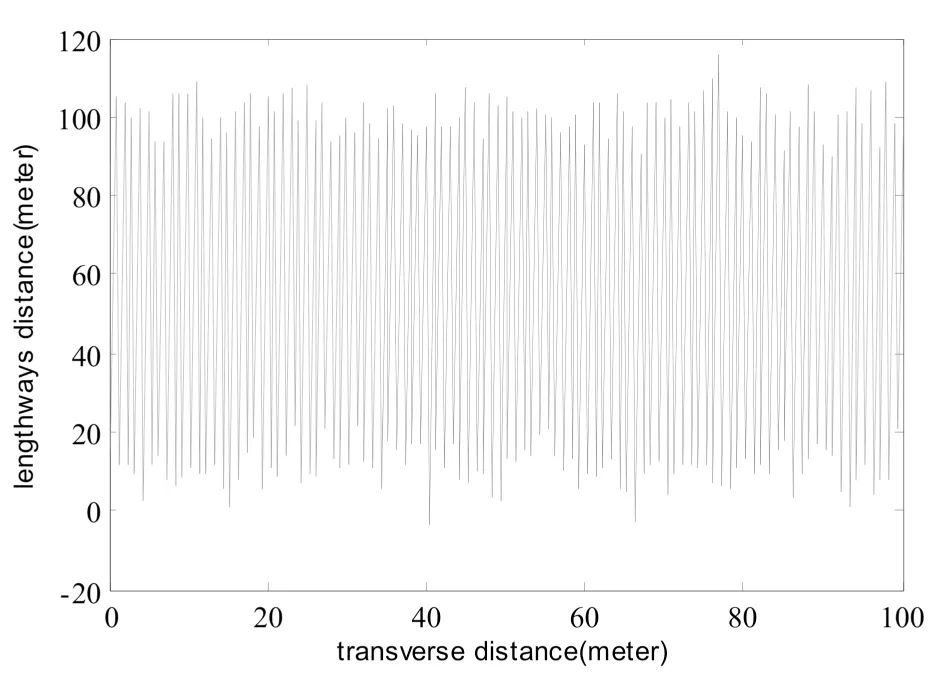
图6 初始路径

2.4 惩罚策略的实现

为了有效地减少种群中违反约束的非可行解的个数，惩罚策略必须采用合适的遗传因子和设计合理惩罚函数[14，15]。设Pi,j为随机路径点，P'i,j为该点对应的障碍物边缘点，如图7所示。

图7 惩罚策略的实现示意图

惩罚函数φ(vi)为

(3)

则

(4)

其中：yi，j为Pi，j点纵坐标值，y'i，j为P'i，j点纵坐标，两点纵坐标通过声纳设备测定；ξ为函数的惩罚因子，取值为2。函数子项φi，j是被惩罚点与障碍物区与平坦区的交界处的函数距离。该点离边界越远，惩罚力度就越大。

2.5 路径适应度函数的确定

适应度函数是搜索进化过程评估群体成员优劣程度的标准，直接影响遗传算法的收敛速度和成败[16，17]。为了满足路径规划的特征，本文选取适应度函数时，需着重研究路径的长度和光滑度等参数。

(1)路径的长度

路径长度指标函数如式(5)所示：

(5)

式中，D(vi)为路径长度，yi,j为pi,j点的纵坐标，xi,j为pi,j点的横坐标。

(2)路径的光滑度

路径光滑度指标函数如式(6)所示：

(6)

式中，φ(vi)为路径光滑度，yi,j为pi,j点的纵坐标，xi,j为pi,j点的横坐标。

采矿车转弯时，角度应尽可能的小，生成的路径越光滑越有助于采矿车运行。故路径转角差累积值φ(vi)越小的成员越优先级越高。

路径长度指标函数和路径光滑度指标函数均取最小值时，路径长度指标函数和路径光滑度指标函数通过线形相加得初始目标函数。

fit'(vi)=αD(vi)+βφ(vi)

(7)

将惩罚函数代入初始目标函数中得终点函数。

fit(vi)=αD(vi)+βφ(vi)+γφ(vi)

(8)

其中，fit( )为路径最优函数 ，α、β、γ分别为长度指标函数、光滑度指标函数和惩罚函数的加权系数。

理想的路径需满足：1)位于可行域内，2)路径光滑，3)路程短，所以终点函数的最优解为全局最小值。

适应度函数采用改进的界限构造法算出终点函数的全局最小值

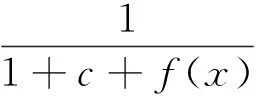
(9)

其中，c为终点函数界限的保守预测值。

在路径规划中f(x)恒>0，故式(9)可改写为：

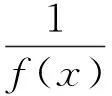
(10)

当路径规划的初始阶段，f(x)值较大，Fit(f(x))的改变需要f(x)巨大的变量才能实现。当路径规划处于终了阶段时，f(x)值很小，f(x)的细小变量将导致Fit(f(x))显著改变。

因此适应度为：

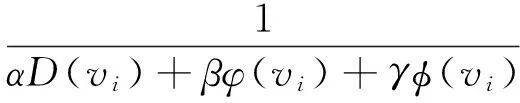
(11)

将求取全局最小值的终点目标函数映射为适应度函数。

2.6 选择方式

选择是从群体中优胜劣汰的操作过程。轮盘法是遗传算法中应用最广泛的选择方法，即轮盘上的每个扇形分区与群体中的每个成员一一对应，且分区面积与对应成员的适应度成正比。轮盘旋转一次即可从群体中选择一个成员。

pi=fi/∑fi

(12)

式中，第i成员被选中的概率为pi；第i成员的适应度为fi；群体的累加适应度为∑fi。由式(12)推算可知，适应度值越高的成员，被选中的概率越大。

本文采用轮盘选择法研究路径规划问题的步骤如下：

设第i个染色体为vi，按出现的次序累计群体内所有染色体的适应度函数值Fit(vi)，得到累计值sum：

(13)

染色体的选择概率p(vi)如式(14)：

(14)

累积选择概率q(vi) 如式(15)：

(15)

r为[0，1]内均匀分布的伪随机数；若r≤q(vi)，则选择染色体vi，否则，选择第k个染色体vk，，满足q(vk-1)

2.7 新个体产生方式

遗传算法中新个体的产生模拟子代染色体产生的方式，即通过交叉和变异的方法产生子代。具体算法如下：

(1)交叉

交叉是遗传算法中产生子代的主要方法。群中染色体配对后，染色体对中各元件按照式(16)进行交叉，从而产生子代染色体的相应元件。

y'i,k=λ1,kyi,k+(1-λ1,k)yj,ky'j,k=λ2,kyj,k+(1-λ2,k)yi,k

(16)

生成的子代染色体如式(17)所示。

vi=(y'i,0,y'i,1,…,y'i,n-1)vj=(y'j,0,y'j,1,…,y'j,n-1)

(17)

其中，yi,k，yj,k为亲代染色体元件，y'i,k，y'j,k为子代染色体元件，λ1,k，λ2,k为随机获取的交叉系数，且0<λ1，λ2<1[18，19]。

(2)变异

变异是指将染色体的基因被等位基因替换得到子代染色体的过程[19]。变异算法能够维持路径规划的多样性。但路径规划又具有特殊性：在初始阶段，需采用较大的变异量以增大遗传搜索范围；而在后期，需缩小变异幅度，仅对接近最优解的基因进行微调。因此本文设计了一种随着搜索推进而变异逐渐减小的遗传算法。

设染色体为vi，基因yi,j以某种概率变异，则生成的子代为：

v'i=(yi,0,yi,1,…y'i,j,yi,n-1)

(18)

其中，y'i,j以下列两种方式变异：

y'i,j=yi,j+Δ(t,y"i,j-yi,j)y'i,j=yi,j-Δ(t,yi,j-y'i,j)

(19)

式中，y"i,j，y'i,j分别是yi,j的最大和最小值。设函数Δ(t,y"i,j-yi,j)和Δ(t,yi,j-y'i,j)的统一形式为Δ(t,y)(式18)，则Δ(t,y)随着t的增加而趋近于0。

Δ(t,y)=y*r*(1-t/T)b

(20)

其中，r是[0，1]中的任何数，T是最长搜索时间，t为当前搜索时间，b是非均匀度参数。

由式(20)可知，在初始阶段，t/T趋近于0，变异值Δ(t,y)趋近最大值，路径搜索范围最大；在结尾阶段，t/T趋近于1，Δ(t,y)则逐渐趋于0，相当于仅在已有搜索结果上增加细小的校正。该变异算法既在前期促进了遗传搜索的进行，又在后期保护了现有的搜索结果。

2.8 仿真试验与结果分析

本文采用遗传算法规划了采矿车避障路径，并通过仿真实验验证其效率和准度。

如图8所示，验证仿真程序由VC++ 6.0语言编写，部分参数设为：种群规模为10，交叉概率为0.7，变异概率0.2。图9中两个椭圆体代表障碍物，A，B和C图分别表示第10次，第20次和第40次迭代运算的结果。结果表明，随着迭代次数的增加，路径性能得到改善，规划的路径也更为精确。由此可见，获得比较。

优越的可行驶路径仅需通过40代的迭代运算，从而说明遗传算法在路径规划研究中的适用和高效。

3 结论

采矿车路径规划问题是开采钴结壳矿产资源的关键问题之一。本文在完善的总体方案框架内，通过系统研究遗传算法各要素，设计并采用仿真程序验证了采矿车最优化路径规划方案，从而证明了遗传算法在钴结壳采矿车路径规划研究中的可行性和高效性。

图8 基于遗传算法的避障路径规划仿真程序流程图

图9 遗传算法仿真路径规划图

[1] 沈裕军，钟祥，贺泽全．大洋钻结壳资源钴究开发现状[J]．矿冶工程，1999， (2)．

[2] Yamazaki T.&T.Sharma. Distribution characteristics of CO-rich manganese deposition sea-mountain the central Pacific Ocean [J]．MarineGeoresources&Geotechnology，1998， (4)．

[3] Manheim F. T.Marine Cobalt Resources [J]．Science，1986，(4750)．

[4] James Hein. Cobalt rich ferro manganese crusts：global distribution composition，origin and Research activities．Poly metallic massive sulphides and cobalt-rich ferromanganese crusts：status and prospects[R]．ISATechnicalstudy，2000，(2)．

[5] 张捍东，郑睿，岑豫皖．机器人路径规划技术的现状与展望[J]．系统仿真学报，2005，(17).

[6] Nilsson N.A mobile automation：An application of artificial intelligence techniques[A]．Proceedingsofthe1stInternationalJointConferenceonArtificialIntelligence[C]，Washington，USA，1969.

[7] 王随平，朱燕春．基于GAAA算法的深海集矿车的最优路径规划[J]．计算机测量与控制, 2008，(1)．

[8] 陈峰．深海底采矿机器车运动建模与控制研究[D]．长沙：中南大学，2005．

[9] 张文修，梁怡．遗传算法的数学基础[M]．西安：西安交通大学出版社，2000．

[10] 刘勇，康立山，陈毓屏．非数值并行算法(第二册遗传算法)[M]．北京：科学出版社，2000．

[11] 吴卫国，陈辉堂．非完整轮式移动机器人控制研究[A]．1997中国控制与决策年会[C]，1997．

[12] 郑月锋．遗传算法在求解时间表问题中的应用研究[D]．杭州：浙江工业大学, 2005．

[13] 卢迎春，桑恩方．基于主动声纳的水下目标特征提取技术综述[J]．哈尔滨工程大学学报，1997，(6)．

[14] Deb K. & S.Agrawal. A niched～penalty approach for constraint handling in genetic algorithms[A]．ProceedingsoftheICANNGA[C], Portoroz, Slovenia, 1999．

[15] Kazarlis S. A., S.E.Papadakis & J. B.Theocharis. Microgenetic algorithms as generalized hill-climbing operators for GA optimization[J]．EvolutionaryComputation, 2001，(3)．

[16] Krishnakumar k.,&D. E.Goldberg Control system optimization using genetic algorithms[J]．JournalofGuidance．ControlandDynamics，1992, (3)．

[17] Michalewicz Z．GeneticAlgorithms+DataStructures=EvolutionProgram[M]． New York: Springer-Verlag, 1996．

[18] Richard J.B.GeneticAlgorithmsandInvestmentStrategies[M]． New York: John Wiley & Sons, 1994．

[19] Allbrecht R., C.Reeves & N.Steele.ArtificialNeuralNetsandGeneticAlgorithms[M]．New York:Springer-Verlag, 1993．

[编校：杨 琴]

Path Planning Research Based on Genetic Algorithm for Cobalt-rich Crust Mining Vehicles

CHEN Bo

(ChangshaAeronauticalVocationalandTechnicalCollege，ChangshaHunan410124)

The cobalt-rich crust, a marine resource with an economic value and a strategic importance, is blocked to be mined by the complicated landform. The current paper focused on the path planning based on genetic algorithm which was a critical question of the cobalt-rich crust mining system.

cobalt-rich crust mining vehicle；path planning；genetic algorithm

2014-10-21

陈波(1979- )，女，湖南衡阳人，讲师，工学硕士，研究方向为机械电子工程。

U442.4

A

1671-9654(2014)04-046-07