分数阶微分双参数黏弹性地基矩形板动力响应
寇 磊, 白 云
(同济大学 地下与建筑工程系,上海 200092)
分数阶微分双参数黏弹性地基矩形板动力响应
寇 磊, 白 云
(同济大学 地下与建筑工程系,上海 200092)
基于弹性地基Pasternak双参数模型,利用分数阶微分得到黏弹性地基双参数模型,并在此基础上建立采用分数阶微分Kelvin模型的双参数黏弹性地基上弹性和黏弹性矩形板在动荷载作用下的动力方程;利用Galerkin方法和分段处理的数值计算方法求解四边简支的弹性和黏弹性地基板的动力方程,通过自由振动算例验证该求解方法的正确性;并分析冲击动荷载作用下分数阶微分Kelvin模型的分数阶、粘滞系数、水平剪切系数和模量参数对位移响应的影响。结果表明:分数阶微分黏弹性模型可以描述不同黏弹性材料的力学行为;分数阶取值0.5前后,矩形板位移响应值出现了不同的衰减发展形态;粘滞系数、水平剪切系数和模量系数取值越大,位移响应衰减速度越快。
分数阶微分;黏弹性地基;双参数模型;动力响应;参数影响
parametric influence
动荷载作用下地基上板的动力响应是刚性路面板、机场跑道、船坞底板和码头平台等实际工程中常见的一类问题,因而得到了广泛重视和大量研究[1-6]。目前,在研究地基与上部结构相互作用的理论中,常采用的地基计算模型主要有Winkler模型、弹性半空间模型以及双参数模型,双参数模型即克服了Winkler模型中地基变形不连续的缺陷,又在数学计算上比半空间模型易于处理[5-7];绝大多数研究在描述土体变形随时间变化的流变性质时采用流变经验公式、流变元件模型和经典黏弹性模型,而实际天然地基土体的力学特性受众多因素影响,其应力与应变呈现明显的非线性及随时间变化的特性;鉴于分数阶微积分非常适合于刻画具有记忆和遗传性质的材料和过程[8],采用分数微积分来描述软土的流变本构关系逐渐得到广泛应用[9-13]。
本文基于分数阶微积分,建立双参数黏弹性地基模型,在此基础上对地基上薄板在动荷载作用下进行分析,并对影响动力响应的各个参数进行讨论,为实际工程中地基与上部结构的动力相互作用分析提供理论基础。
1 分数阶微分双参数黏弹性地基矩形板受荷动力方程
1.1 分数阶微分双参数黏弹性地基
采用分数阶微积分理论中的Riemannn-Liouville 分数阶算子[14],对于函数f(t)的α阶微分定义为
(1)
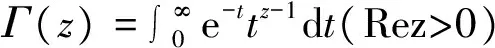
设f(t)至少存在一阶导数连续,并令t0=0,式(1)展开为
(2)
由式(2)可知,分数阶微分作用于函数f(t)等于Abel核Ir(t)与函数f(t)的广义Stieltjes卷积。
对于黏弹性材料,其积分型本构方程为
(3)
式中,J(t)为蠕变柔量;σ(t)为应力;ξ(t)为应变。
由式(2)和式(3)可知, R-L分数阶微分与描述黏弹性材料的积分型本构方程表达形式是一致的。
天然地基在荷载作用下的沉陷变形具有明显的时间效应,地基土体介于理想固体和理想流体之间,因而考虑采用分数阶微分描述地基土体的黏弹性特征更符合实际状况。根据Pasternak 提出的双参数弹性地基模型[15],假定黏弹性地基土体在水平剪切层(x-y面)为均质各向同性,并同时考虑地基在传递上部结构变形时随时间变化的影响,如图1所示,得到剪切层每单位宽度上的剪切力为:

图1 黏弹性地基双参数模型Fig.1 The two-parameter viscoelastic foundation
(4)
式中,Nx、Ny为剪切力;τxz、τyz为剪应力;Dα为R-L分数阶微分算子;μ为水平剪切系数,与剪切层变形有关;wd(x,y,t)为地基的沉陷。
根据Padovan得到的分数阶微分黏弹性本构方程[16],即
Sσ(t)=Qξ(t)
(5)
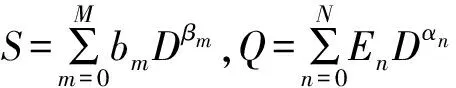
得到黏弹性地基土体竖向弹簧层的作用力为
R=S-1Qwd(x,y,t)
(6)
同时建立z方向力的平衡方程,即
(7)
将式(4)和式(6)代入方程(7)中,得到黏弹性地基与上部结构之间的相互作用力q(x,y,t),即:
q(x,y,t)=S-1Qwd(x,y,t)-μDα2wd(x,y,t)
(8)
若令式(5)中M=N=1,b1=0则式(5)简化为:
σ(t)=E0ξ(t)+E1Dαξ(t)=kξ(t)+ηDαξ(t)
(9)
式(9)称为分数阶微分Kelvin模型,该模型由模量系数为k的Hook弹簧和粘滞系数为η含分数阶α的Newton粘壶并联而成,如图2所示。当α=1时,即为经典Kelvin模型。
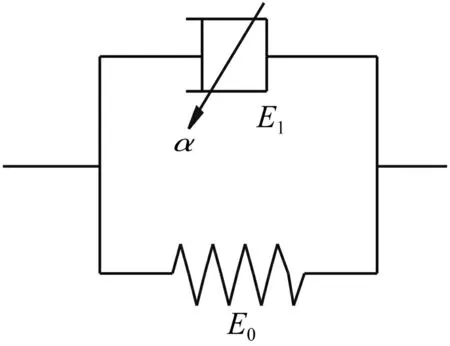
图2 分数阶微分Kelvin模型Fig.2 Fractional derivative Kelvin model
将式(9)代入式(8)得到采用分数阶微分Kelvin模型的q(x,y,t)的表达式,即
q(x,y,t)=kwd(x,y,t)+
ηDαwd(x,y,t)-μDα2wd(x,y,t)
(10)
1.2 双参数黏弹性地基上黏弹性薄板受荷动力方程
对于黏弹性地基上的均质各向同性黏弹性薄板,设其体积变形为弹性变形,即
σkk(t)=3Kξkk(t)
设其纯剪切变形符合分数阶微分Kelvin模型,即
Sij(t)=2(G+η′Dβ)eij
式中,K为体积模量;G为剪切模量;η′为黏性系数;Dβ为R-L分数阶微分算子。
根据薄板ξz=0得到
(11)
基于kirchhoff薄板理论,可得
(12)
当地基板上受动荷载p(x,y,t)作用,薄板的动力控制微分方程为
(13)
式中,w(x,y,t)为板的变形;q(x,y,t)为地基与板之间的相互作用力;ρ,h为板的单位密度和厚度。
将式(12)和式(10)代入方程(13),根据变形协调条件wd=w,得到采用分数阶微分Kelvin模型的双参数黏弹性地基上黏弹薄板的动力方程,即
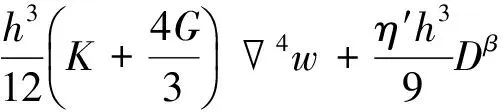
(14)
1.3 双参数黏弹性地基上弹性薄板动力方程
对于黏弹性地基上的均质各向同性弹性薄板,根据kirchhoff薄板理论,得到
(15)
将式(15)和式(10)代入方程(13),得到采用分数阶微分Kelvin模型的双参数粘弹性地基上弹性薄板的动力方程,即
D4w+kw+ηDαw-μDα2w+
(16)
2 动力方程求解
对于板四边简支情况,如图3,边界条件为
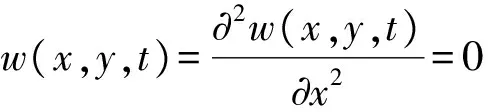
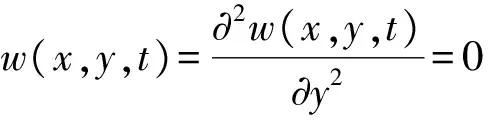
初始条件为
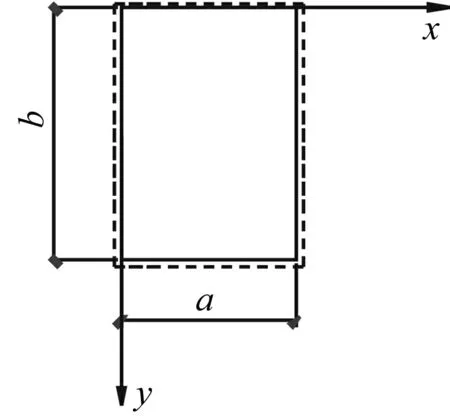
图3 四边简支板Fig.3 Plate with four edges simply supported
由于非线性偏微分-积分方程(14)、(16)难以求解,采用Galerkin方法进行简化,在边界条件下,方程(14)、(16)的解可展开为三角级数形式
(17)
将式(17)代入式(14),得到:
AT″(t)+BT(t)+CDβT(t)+EDαT(t)=Ff(t)
(18)
式中,

将式(18)变化为
(19)
先计算方程组(19)出现的分数阶微分项DβT(t)、DαT(t),现以DαT(t)为例。
根据R-L分数阶微分的定义可知,设T(t)至少存在一阶导数连续,则
(20)
(21)
被积函数在S1的定义域中处处有定义,由复化梯形求积公式直接求得[17]。
n≥3
(22)
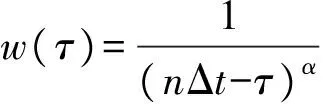
(23)
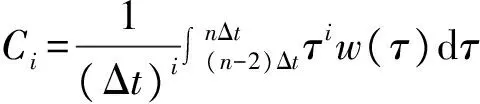
由式(20)、式(22)和式(23)求出分数阶微分项DαT(t),同理求出分数阶微分项DβT(t)。对于方程组(19),将计算时间t进行离散t=nΔt,Δt为等距步长;先用Euler方法计算起始3步的值,然后用改进的四步Adams预估-校正算法进行计算。
方程(16)同样按上述方法进行求解。
3 算例及参数讨论
3.1 求解自由振动
采用R-L分数阶微分算子的黏弹性振子的自由振动,其微分方程及初始条件为[19]
(24)
式中,f(t)为位移函数;a,b为常数。当α=1/2时,方程(24)的解析解为[17]
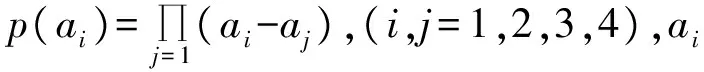
采用本文提出的分数阶微分数值算法Matlab编程求解方程(24),计算中选取a=0.2,b=1。并将计算结果与该方程的解析解进行对比,如图4所示。
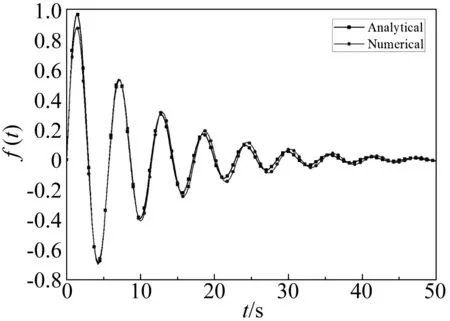
图4 分数阶自由振动的解析解与数值解对比Fig.4 The comparison between the analytical and numerical solution of fractional free vibration
从图4可知,本文的数值计算结果与精确解相当吻合,从而验证了本文求解分数阶微分方程数值方法的正确性。
3.2 求解冲击动载作用
放置在黏弹性地基上的四边简支弹性矩形薄板,板中心处受到冲击动载作用,冲击荷载采用半波余弦曲线表示,其荷载表达式为
p(x,y,t)=
式中,p0为加载峰值,T为荷载冲击周期,x0,y0为板中心坐标。
利用Matlab编程计算t=0~50 s的地基板中心的位移响应及平行x轴的板中心轴线在t=25 s、t=50 s的位移响应值。计算时选取p0=100 kN,T=0.1 s,板和地基相应参数如表1。由于一阶和高阶Galerkin截断得到的动力学行为定性相同[20],为简化计算,令m=1,n=1。计算结果如图5、图6所示。

表1 矩形板及地基参数
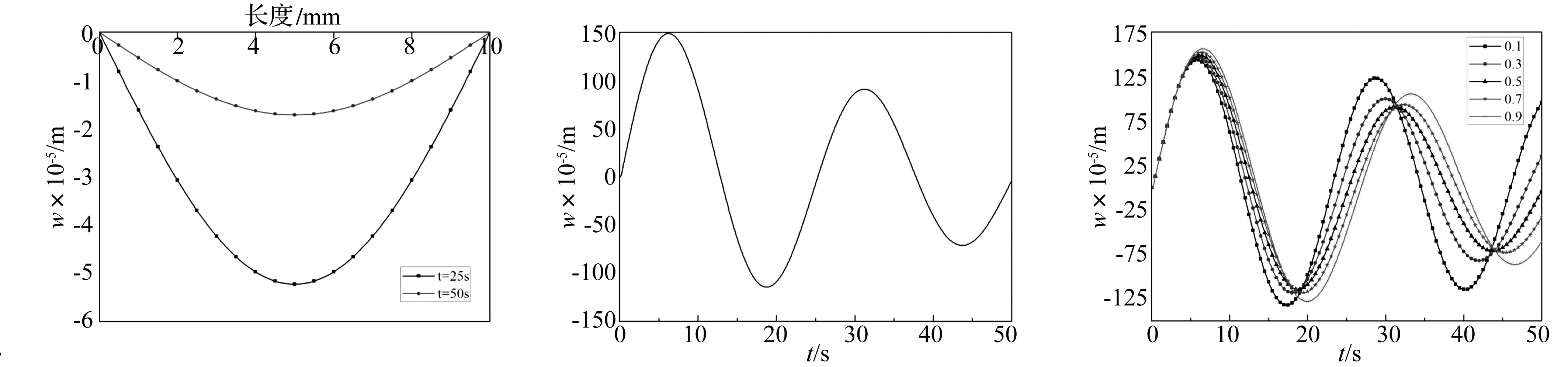

图5 t=25s、t=50s时板中心轴线的位移响应曲线Fig.5Thedisplacementcorrespondingcurvesofcentrallineoftheplateatt=25sandt=50s图6 t=0-50s时板中心的位移响应曲线Fig.6Thedisplacementcorrespondingcurvesoftheplatecenteratt=0-50s图7 不同α取值时板中心位移响应时间曲线Fig.7Thedisplacementcorrespondingcurvesattheplatecenterunderdifferentαvalue
由图5可知,地基薄板在冲击荷载作用下沿平行x轴的中心轴线的位移响应以板中心位置两端对称分布,位移响应值从端部向板中心区域发展,板中心位置达到最大值;随着时间的发展,位移响应值衰减明显。由图6可知,板中心的位移响应值随着冲击荷载作用迅速增大,当地基板不在受冲击荷载作用即t>0.1 s后,位移值继续增大,在t=7 s左右达到最大值,随后位移振幅衰减明显,但衰减周期保持不变。
3.3 参数分析
在冲击荷载算例的基础上,以下将逐一研究分数阶α、粘滞系数η、水平剪切系数μ和模量系数k对地基板动力位移响应的影响,在讨论某一个参数时,其它参数值保持不变。
将分数阶α分别取为0.1、0.3、0.5、0.7,0.9,计算t=0~50 s时薄板中心处的位移响应值及t=50 s时薄板平行x轴的板中心轴线的位移响应值,计算结果如图7、图8所示。
由图7可知,分数阶α值越大,板受到的阻尼越小,板中心位移响应达到初始峰值的时间越长,初始峰值也越大;随着分数阶α值的不断增大,由于板受到的阻尼不断变小,位移振幅衰减周期越来越长;当α<0.5时位移响应振幅的衰减明显,当0.5<α<1位移响应振幅的衰减逐渐放缓。
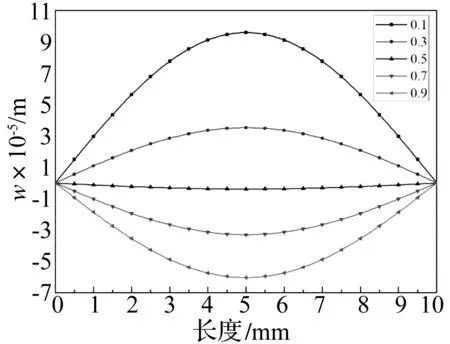
图8 t=50 s时板中心轴线的位移响应曲线图Fig.8 The displacement corresponding curves of central line of the plate of t=50 s under different α values
由图8可知,分数阶α的取值对板的位移响应发展形态有较大影响;分数阶α取值的不同,板中心轴线的位移响应均以板中心位置两端对称分布,板中心为绝对值最大位置,但位移响应的性质却发生了变化:当α<0.5时位移响应为正值,α值越大,同一位置处位移响应越小;当0.5<α<1时,位移响应为负值,α值越小,同一位置处位移响应越小;其中,当分数阶α→1时逐渐退化为采用经典Kelvin模型的薄板位移响应情况。由以上分析可知,通过改变分数阶α值的大小可以反映不同黏弹性材料的力学行为,分数阶α值可以根据材料的流变实验数据拟合得到,采用分数阶黏弹性模型比经典黏弹性模型更能很好的反映黏弹性材料的力学性质。
将粘滞系数η分别取为1 MN/m3、10 MN/m3、45 MN/m3、100 MN/m3,计算t=0~50 s时薄板中心处的位移响应值,计算结果如图9所示。
由图9可知,粘滞系数η值越大,板受到的阻尼越大,板中心位移响应达到初始峰值的时间越短,初始峰值也越小;随着粘滞系数η值的不断增大,位移响应振幅的衰减越来越剧烈,振幅衰减速度也越快,衰减周期越来越小。
将水平剪切系数μ分别取为0、100 MN/m3、250 MN/m3、500 MN/m3,计算t=0~50 s时薄板中心处的位移响应值,计算结果如图10所示。
由图10可知,当μ=0即为Winkler模型的位移响应值;水平剪切系数μ值越大,板受到的阻尼越大,板中心位移响应达到初始峰值的时间越短,初始峰值也越小;随着水平剪切系数μ的不断增大,位移响应振幅的衰减越来越剧烈,振幅衰减速度也越快,衰减周期越来越小。
将模量系数k分别取为5 MN/m3、20 MN/m3、50 MN/m3、100 MN/m3,计算t=0~50 s时薄板中心处的位移响应值,计算结果如图11所示。
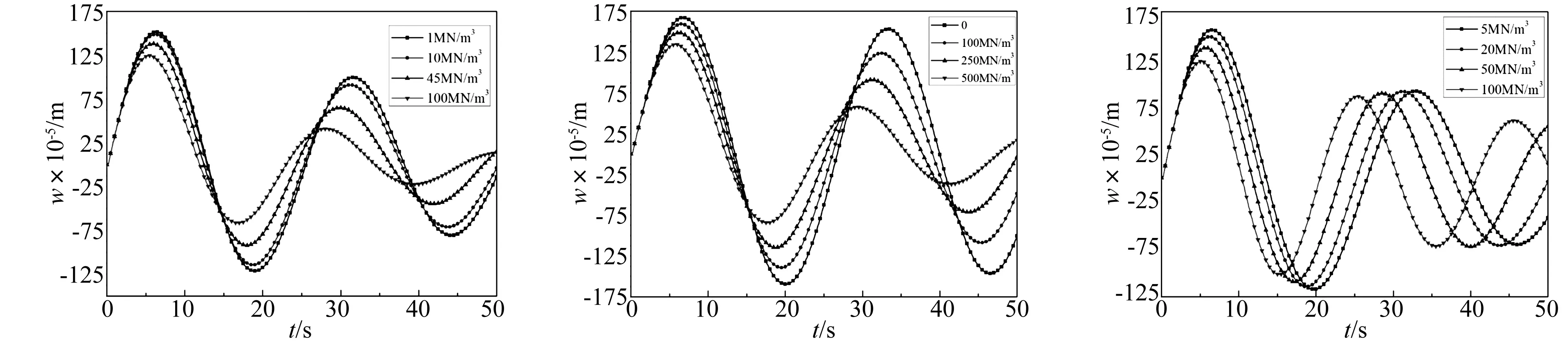

图9 不同η取值时板中心位移响应时间曲线Fig.9Thedisplacementcorrespondingcurvesattheplatecenterunderdifferentηvalue图10 不同μ取值时板中心位移响应时间曲线Fig.10Thedisplacementcorrespondingcurvesattheplatecenterunderdifferentμvalue图11 不同k取值时板中心位移响应时间曲线Fig.11Thedisplacementcorrespondingcurvesattheplatecenterunderdifferentkvalue
由图11可知,模量系数k值越大,板中心位移响应达到初始峰值的时间越短,初始峰值也越小;随着模量系数k的不断增大,位移响应振幅的衰减越来越明显,振幅衰减速度也变快,衰减周期越小。
4 结 论
基于分数阶微分理论、黏弹性理论和上部结构与地基相互作用理论,研究了分数阶微分双参数黏弹性地基矩形板的动力响应问题, 并讨论了分数阶、粘滞系数、水平剪切系数和模量参数对位移响应的影响,得到的主要结论有:
(1) 提出的求解分数阶微分双参数黏弹性地基上薄板动力方程的数值方法,可以推广到求解黏弹性地基上其它结构形式的动力响应问题;
(2) 分数阶微分黏弹性模型可以较大范围描述不同黏弹性材料的力学行为;
(3) 薄板动荷载作用下位移响应值随着时间的发展出现衰减现象;分数阶α取值在α=0.5前后,薄板位移响应值出现了不同的衰减发展形态;粘滞系数η、水平剪切系数μ和模量系数k取值越大,薄板位移响应衰减速度越快,衰减周期越小,其中,粘滞系数η、水平剪切系数μ起主导作用;
(4) 在实际应用中,需要根据不同地基土类型的力学特性,选取合理的分数阶微分黏弹性模型机确定其相应参数的取值范围。
[ 1 ] Zaman M, Taheri M R, Alvappillal A. Dynamic response of a thick plate on viscoelastic foundation to moving loads[J].International Journal for Numerical Analysis and Method in Geo-mechanics,199l,15(9):627-647.
[ 2 ] 祝彦知,薛保亮,王广国.粘弹性地基上粘弹性地基板的自由振动解析[J].岩石力学与工程学报,2002,21(1):112-118. ZHU Yan-zhi, XUE Bao-liang, WANG Guang-guo. Free vibration analysis of viscoelastic foundation plate on viscoelastic foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(1):112-118.
[ 3 ] Sun L. Dynamic response of kirchhoff plate on a viscoelastic foundation to harmonic circular loads[J].Journal of Applied Mechanics, 2003, 70(4):595-600.
[ 4 ] Kim S M, McCullough B F. Dynamic response of plate on viscous Winkler foundation to moving loads of varying amplitude [J].Engineering Structures, 2003, 25(9):1179-1188.
[ 5 ] 张选兵,罗先启,葛修润,等. 双参数弹性地基上板承受冲击荷载的动力响应的解析解[J].岩石力学与工程学报,2001, 20(6),846-850. ZHANG Xuan-bing, LUO Xian-qi, GE Xiu-run, et al. Analytical solution on dynamic response of rectangular plate with free edges of two parameters elastic foundation under impact load [J].Chinese Journal of Rock Mechanics and Engineering,2001(11), 20(6):846-850.
[ 6 ] 颜可珍,夏唐代,黄立葵.双参数粘弹性地基无限长板的瞬态动力响应分析[J].岩石力学与工程学报, 2005,24(24):4576-4580. YAN Ke-zhen, XIA Tang-dai, HUANG Li-kui. Dynamic response of strip on two-parameter viscoelastic foundation under impact loading [J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24):4576-4580.
[ 7 ] 彭丽,丁虎,陈立群.黏弹性Pasternak地基梁振动的复模态分析[J].振动与冲击,2013,32(2):143-146. PENG Li, DING Hu, CHEN Li-qun. Complex modal analysis for vibrations of a beam on a viscoelastic Pasternak foundation[J].Journal of Vibration and Shock 2013,32(2):143-146.
[ 8 ] 王东生,曹磊. 混沌、分形及其应用[M].合肥:中国科学技术大学出版社,1995.
[ 9 ] 孙海忠,张卫. 一种分析软土黏弹性的分数导数开尔文模型[J].岩土力学,2007,28(9):1983-1986. SUN Hai-zhong, ZHANG Wei. Analysis of soft soil with viscoelastic fractional derivative Kelvin model [J]. Rock and Soil Mechanics, 2007, 28(9):1983-1986.
[10] 殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1899-1903. YIN De-shun, REN Jun-juan, HE Cheng-liang, et al. A new rheological model element for geo-materials[J].Chinese Journal of Rock Mechanics and Engineering, 2007,26(9):1899-1903.
[11] 刘林超,杨骁.,竖向集中力作用下分数导数型半无限体粘弹性地基变形分析[J].工程力学,2009,26(1):13-17. LIU Lin-chao, YANG Xiao. Analysis on settlement of semi-infinite viscoelastic ground based on fractional model[J]. Engineering Mechanics, 2009, 26(1):13-17.
[12] 何利军,孔令伟,吴文军,等.采用分数阶导数描述软黏土蠕变的模型[J].岩土力学,2011,32(增刊2):239-243. HE Li-jun, KONG Ling-wei, WU Wen-jun, et al. A description of creep model for soft soil with fractional derivative [J]. Rock and Soil Mechanics, 2011, 32(S2):239-243.
[13] 寇磊.分数阶微分型双参数黏弹性地基矩形板受荷响应[J].力学季刊,2013,34(1):154-160. KOU Lei. Response of rectangular plate on fractional derivative two-parameter viscoelastic foundation[J].Chinese Journal of Mechanics,2013,34(1):154-160.
[14] Samko S G, Kilbas A A, Marichev O L. Fractional integrals and derivatives: theory and application[M].USA: Gordon and Breach Science Publishers, 1993.
[15] Arnold D K. Elastic and viscoelastic foundation models [J].Journal of Applied Mechanics, 1964, 31(3):491-498.
[16] Padovan J. Computational algorithm for FE formulations involving fractional operators [J].Computational Mechanics, 1987, 2(4):271-287.
[17] 张卫,徐华,清水信行.,分数算子描述的黏弹性体力学问题数值方法[J].力学学报,2004,36(5):617-622. ZHANG Wei, XU Hua, Shimizut N. The numerical analysis formulation of the viscoelastic solid modeled by fractional operator[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(5):617-622.
[18] 朱正佑,李根国,程昌钧. 分数积分的一种数值计算方法及其应用[J].应用数学和力学,2003,24(4):331-341. ZHU Zheng-you, LI Gen-guo, CHENG Chang-jun. A numerical method for fractional integral with applications[J]. Applied Mathematics and Mechanics, 2003, 24(4):331-341.
[19] Sakakibara S. Properties of vibration with fractional derivative damping of order 1/2[C] //JSME International Journal, Series C: Dynamics, Control, Robotics, Design and Manufacturing, Japan, Iwaki-Meisei University, 1997:393-399.
[20] 陈立群,程昌钧. 非线性粘弹性梁的动力学行为[J].应用数学和力学,2000,21(9):897-902. CHEN Li-qun, CHENG Chang-jun. Dynamical behavior of nonlinear viscoelastic beams[J].Applied Mathematics and Mechanics,2000,21(9):897-902.
Dynamic response of rectangular plates on two-parameter viscoelastic foundation with fractional derivatives
KOU Lei, BAI Yun
(Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China)
Based on a two-parameter Pasternak model of elastic foundation, a two-parameter model of viscoelastic foundation was derived by using fractional derivatives. The dynamic equations of elastic and viscoelastic rectangular plates on a two-parameter viscoelastic foundation with the fractional Kelvin model under dynamic loads were established. The dynamic equations of elastic and viscoelastic rectangular plates with four-edge simply supported were solved with Galerkin method and the segmented numerical method, the correctness of the solutions was verified with examples of free vibration. The influences of fractional order, viscosity parameter, horizontal shear coefficient and modulus of the fractional Kelvin model under an impact load on the displacement responses of the plates were analyzed. The results showed that the fractional derivative viscoelastic model can describe the mechanical behavior of different viscoelastic materials; the displacement responses of the rectangular plates have different attenuation forms before and after the fractional order value of 0.5; the attenuation speed of the displacement response increases with increase in viscosity coefficient, horizontal shear coefficient and modulus.
fractional derivative; viscoelastic foundation;two-parameter model; dynamic response;
教育部长江学者和创新团队发展计划 (IRT1029)
2013-03-25 修改稿收到日期:2013-05-30
寇磊 男,博士生,1983年5月生
TU44
A
10.13465/j.cnki.jvs.2014.08.025

