基于检测系统非线性相关性的相空间重构时间延迟估计
许 岩 , 王 波 , 李 鹏
(1.重庆大学 计算机学院,重庆 400044;2.西昌卫星发射中心,四川 西昌 615000;3.中国电子科技集团 第38研究所,合肥 230051)
基于检测系统非线性相关性的相空间重构时间延迟估计
许 岩1,2, 王 波1, 李 鹏3
(1.重庆大学 计算机学院,重庆 400044;2.西昌卫星发射中心,四川 西昌 615000;3.中国电子科技集团 第38研究所,合肥 230051)
提出一种确定时间延迟参数的新方法,非线性复自相关法。采用一个高次复自相关函数R(τ)检测系统的非线性相关性,通过寻找R(τ)的第一个局部极小值点来确定最优时间延迟。R(τ)时间复杂度低,对数据长度依赖性不强。选取四种典型混沌动力学系统,加入不同噪声水平的高斯白噪声,模拟含噪混沌时间序列,进行数值验证。结果表明,所得结果更合适,同时具有优秀的抗噪声能力。
混沌时间序列;噪声水平;相空间重构;嵌入维数;时间延迟
混沌时间序列分析作为当今非线性科学的重要课题,在计算机网络、生物医学以及金融等科学领域得到广泛应用。分析实际测量得到的时间序列数据混沌特征时,首先必须对其进行相空间重构。目前最为广泛采用的相空间重构方法是基于Takens定理[1]的坐标延迟法[2]。坐标延迟法是通过确定时间延迟τ和嵌入维数m来构造相空间。假设观察得到的时间序列为x(i),i=1,2,3,…,N,则相空间重构为X(i)={x(i),x(i+τ),x(i+2τ),……,x[i+(m-1)τ]},i=1,2,…M,其中M=N-(m-1)τ。对于时间延迟和嵌入维数的选取目前有两种观点,一种观点认为两个参数无关,分别独立计算(理论上,对于无限长的、无噪声干扰的时间序列,τ和m是相互独立的),如自相关法[3]、复自相关法[4-5]、互信息法[6]以及平均位移法[7]。另一种观点认为两个参数相关,通过计算嵌入窗宽tw=(m-1)τ来确定两个参数,如时间窗口法[8]和C-C法[9-11]等,多数研究人员认为这种观点更加适合工程实践。近年来,人们在上述算法的基础上进行了广泛而深入的研究[12-15],这些研究主要以数据充足且无噪声的混沌时间序列为对象,然而实际测量得到的时间序列,一是未必能得到充足的数据点,二是不可避免含有噪声,混杂在混沌动力学系统中的噪声会掩盖混沌系统内在的动力学特性,这两点因素都会影响时间延迟参数的计算。当时间延迟参数取值不是最佳时,虽然不会影响重构的吸引子反应系统的动力学性质,但是时间延迟过大会使非线性预测模型的计算量加大,同时,也会影响到重构吸引子的欧几里得几何形状进而影响关联维数d的计算[16]。
本文分析了几种利用自相关性估计时间延迟的方法,在此基础上,提出一种估计时间延迟的新方法,非线性复自相关法。该方法在几何意义上构造一个与相空间维数相同的多项式空间,在此空间中检测系统的非线性相关性来确定最优时间延迟。
1 自相关法和复自相关法
对于时间序列x(i),i=1,2,3,…,N,自相关法是把J取一个固定值,而后对τ从小到大取值,计算自相关函数R(jτ)(见式(1)),当R(jτ)下降到初始值的1-e-1时,所对应的τ即为时间延迟。
(1)
自相关法本质上是度量时间序列的线性关系,不适合非线性问题[17],同时难于推广到高维,Aguirre[18]对此进行改进,采用线性相关函数Φ1(τ) (见式(2))检测系统的线性相关性,得到时间延迟τ1;同时引入一个非线性相关函数Φ2(τ) (见式(3))检测系统的非线性相关性,得到时间延迟τ2;取τ1和τ2中的最小值作为最优时间延迟,其中,E(·)为数学期望。虽然该方法比自相关法得到的时间延迟更小,然而与其他算法相比,结果仍然偏大。
(2)
(3)
复自相关法是由自相关法和平均位移法相结合推导得出,给定嵌入维数m,对时间延迟τ由小到大取值,计算复自相关函数Rm(τ) (见式(4)),选取Rm(τ)的第一个零点所对应的τ作为时间延迟。为了适应一般系统,采用的是去除时间序列均值的去偏复自相关函数Rx(τ)[4](见式(5))。该方法理论性强,继承了平均位移法的几何意义,同时解决了自相关法不能高维扩展的问题。
(4)
(5)
2 复自相关法分析
复自相关法是对自相关法的高维扩展,从式(2)和式(5)可以看出,当m=2时,Rx(τ)=Φ1(τ),该方法仍然是对线性关系上的相关性进行度量,不能检测到非线性的混沌时间序列中所有状态之间的相关性。因此,该方法所得到的结果偏大。另一方面,由于噪声是相互无关的,所以该方法对噪声不敏感,有很好的抗噪声能力。
为了验证上述推论的正确性,选取Logistic系统Lorenz系统的x分量数据,分别加入不同噪声水平的高斯白噪声,模拟含有噪声的混沌时间序列。噪声水平ν定义为
ν=σ[ω(t)]/σ[x(t)]
(6)
上式中ω(t)是均值为0,方差为1的高斯白噪声,x(t)为纯净的混沌时间序列,σ(·)为时间序列的标准差。
2.1Logistic系统
对Logistic方程
x(n+1)=ux(n)[1-x(n)]
(7)
取u=4,初值取0.6,迭代3 000步,取后面的2 000个数据点作为纯净的混沌时间序列,其关联维数d理论值为0.99[15],根据Takens定理m≥2d+1,最佳嵌入维数m=3。
图1是Logistic系统去偏复自相关函数Rx(τ)在不同噪声水平下的变化关系,如图所示,Rx(τ)对噪声不敏感。计算结果如表1所示,与m=3时最优时间延迟为1[19]的结论相比,结果偏大,相反,该方法的抗噪声能力很好达到60%。

图1 Logistic系统Rx(τ)变化关系Fig.1 Non-bias multiple autocorrelation function of Logistic

V010%20%40%60%80%τ444442
2.2 Lorenz系统
对Lorenz方程
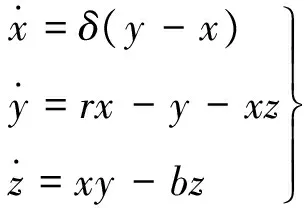
(8)
取δ=16,r=45.92,b=4,初值 (1,0,1),用Runge-Kutta方法求解,步长h=0.005,去除暂态过程,得到一个30 000个点数的值解,从中取出2 000个点作为纯净的混沌时间序列,关联维数d理论值为2.05[15],最佳嵌入维数m=6。
Lorenz系统的去偏复自相关函数Rx(τ)变化关系如图2,Rx(τ)对噪声仍然不敏感。
结果如表2所示,图3是Lorenz吸引子在x-y平面上的投影图,图4是τ=38时变量x的重构吸引子,可以看出,此时吸引子结构被破坏,时间延迟取38偏大。
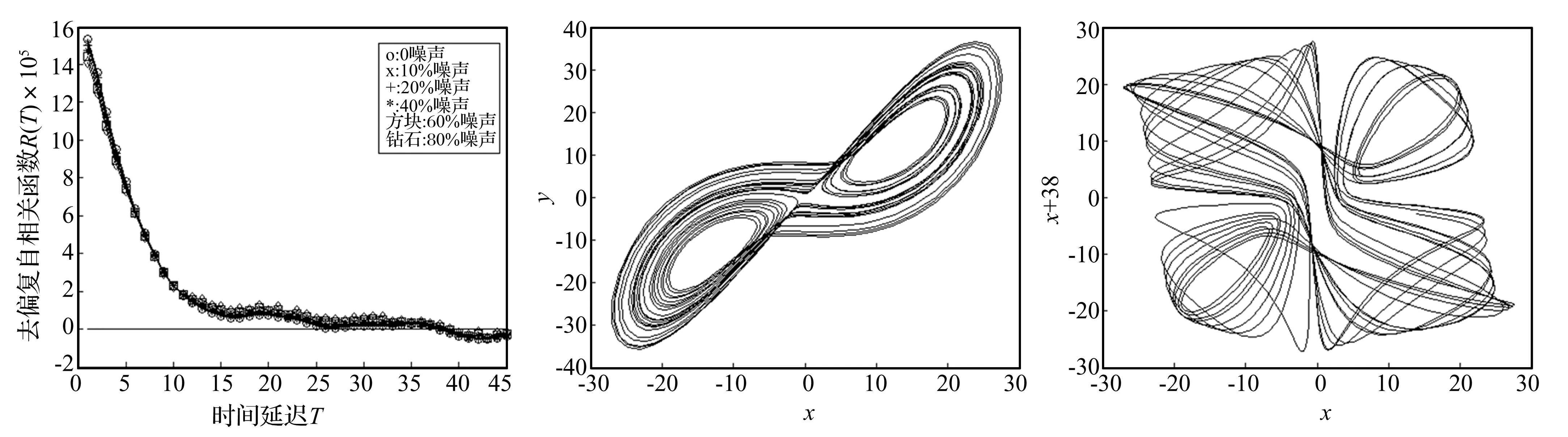

图2 Lorenz系统Rx(τ)变化关系Fig.2non⁃biasmultipleautocorrelationfunctionofLorenz图3 Lorenz吸引子x-y平面投影图Fig.3ProjectionofLorenzstrangeattractoronx-yplane图4 τ=38Lorenz重构吸引子Fig.4ReconstructedattractorofLorenzchoosingτ=38

表2 Lorenz系统计算结果
从以上结果可以看出,复自相关法的计算结果偏大;该方法对噪声不敏感,抗噪声能力很好。这与分析得到的结论一致。
3 非线性复自相关法
复自相关法对混沌系统计算结果偏大的根本原因是,该方法采用一个线性复自相关函数检测系统的相关性,而混沌系统是非线性的。对此,非线性复自相关法采用一个高次复自相关函数R(τ)检测混沌系统的非线性相关性。
从代数几何意义上考虑R(τ)的构造,首先复相关法可以看成是构造一个2维的多项式空间,这对于高维的相空间来说,维数过小,采用该方法计算的结果不准确;对此,非线性复自相关法通过构造一个与重构相空间维数相同的一元n次多项式空间,以准确计算混沌系统的相关性,而一元n次多项式空间在高维空间代数流形上的维数为n+1[20],因此n=m-1。该多项式记为f(x)
f(x)=1+x+x2+…+xm-1
(9)
则R(τ)可表示为
(10)
为了便于计算,取多项式f(x)的近似值xm,R(τ)的最终表达式如下:
(11)
采用坐标延迟法重构相空间,相空间矢量X(i)={x(i),x(i+τ),x(i+2τ),……,x[i+(m-1)τ]}中的任意两个坐标之间必须是独立的。若时间延迟τ若太小,两个分量在数值上太接近,则无法提供两个独立的坐标分量;但时间延迟过大,两坐标分量在统计意义上又是完全独立的,重构出来的混沌吸引子在这两个方向上的投影毫无相关性,造成吸引子结构被破坏。非线性复自相关法选取R(τ)的极小峰值对应的值作为时间延迟,确保任意两个坐标之间的独立性;取其中的最小值作为最优时间延迟,确保吸引子结构不被破坏。
非线性复自相关法的具体计算过程如下。对给定的嵌入维数m,将时间延迟τ由小到大取值,计算非线性复自相关函数R(τ),选取R(τ)的第一个局部极小值点对应的值τ作为最优时间延迟。
R(τ)易于计算,对数据量要求不大,对噪声不敏感,可以检测到Rx(τ)检测不到的时间序列中的变化,能够准确检测到混沌系统的非线性相关性,所以得到的时间延迟更加合适。
4 实验
实验选取Logistic系统、Hennon系统、Lorenz系统和Rossler系统的x分量作为纯净的混沌时间序列,分别加入不同噪声水平的高斯白噪声,模拟含有噪声的混沌时间序列。为了与复自相关法进行对比,利用Logistic系统和Lorenz系统模拟的时间序列数据,分别沿用第二节中的原数据。同时选用互信息法和C-C法与新方法进行比较。
4.1 Logistic系统
仍然取嵌入维数m=3,计算Logistic系统的时间延迟,R(τ)在不同噪声水平下的变化关系如图5所示,R(τ)对噪声不敏感,对照图1可以看出,相比Rx(τ),R(τ)对噪声的敏感度有所增加。表3是三种方法对不同噪声水平下Logistic系统的时间延迟计算结果,从表中可以出,新方法的计算结果与m=3时最优时间延迟为1[19]的结论一致,与复自相关法相比,其抗噪声能力也更好,在噪声水平达到80%时,结果仍然稳定;而互信息法和C-C法的结果也偏大。
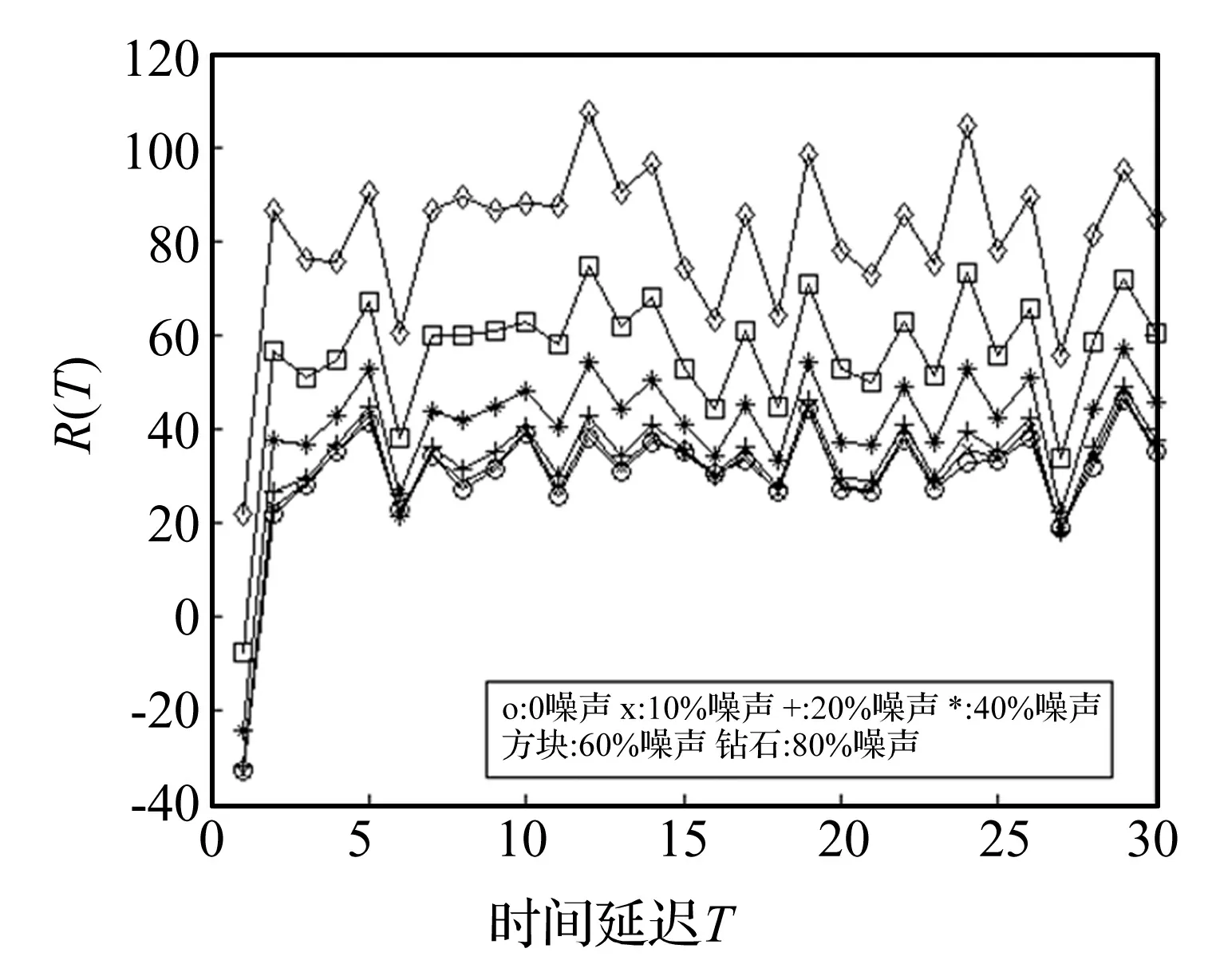
图5 Logistic系统R(τ)变化关系Fig.5 Nonlinear multiple autocorrelation function of Logistic
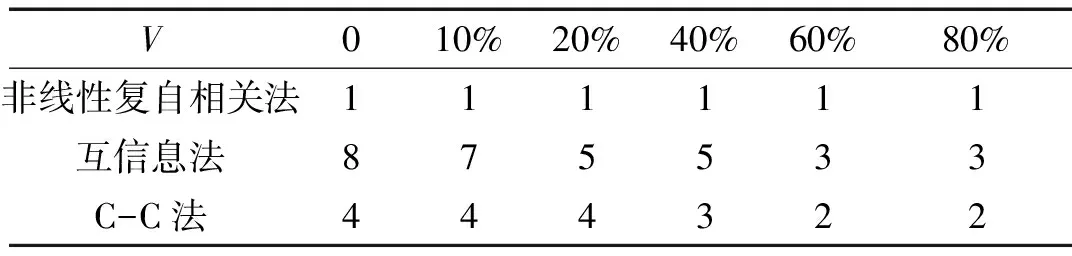
V010%20%40%60%80%非线性复自相关法111111互信息法875533C-C法444322
4.2 Hennon系统
对Hennon方程
(12)
取a=1.4,b=0.3,初值(0.4,0.4),迭代10 000步,取后面的2 000个数据点作为纯净的混沌时间序列,关联维数d理论值为1.25[15],取嵌入维数m=5。
图6是Hennon系统R(τ)在不同噪声水平下的变化关系,从图中可以看出,R(τ)对噪声不敏感。
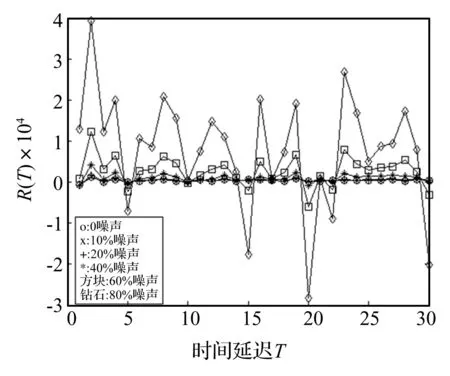
图6 Hennon系统R(τ)变化关系Fig.6 Nonlinear multiple autocorrelation function of Hennon
表4是三种方法对不同噪声水平下Hennon系统的时间延迟计算结果。图7是Hennon吸引子在x-y平面上的投影图,图8是τ=1时变量x的重构吸引子,图9是τ=2时变量x的重构吸引子,显然τ=2偏大,τ取1为最佳时间延迟。同Logistic时一样,互信息法和C-C法的结果偏大。
表4 Hennon系统计算结果


图7 Hennon吸引子x-y平面投影图Fig.7ProjectionofHennonstrangeattractoronx-yplane图8 τ=1Hennon重构吸引子Fig.8ReconstructedattractorofHennonchoosingτ=1图9 τ=2Hennon重构吸引子Fig.9ReconstructedattractorofHennonchoosingτ=2
4.3 Lorenz系统
仍然取嵌入维数m=6计算Lorenz系统的时间延迟,图10和图11是R(τ)在不同噪声水平下的变化关系(由于不同噪声水平下R(τ)的数量级相差过大,放在一张图中无法展示部分曲线变化趋势,因此这里选用两张图),R(τ)对噪声不敏感,对照图3可以看出,相比Rx(τ),R(τ)对噪声更敏感。
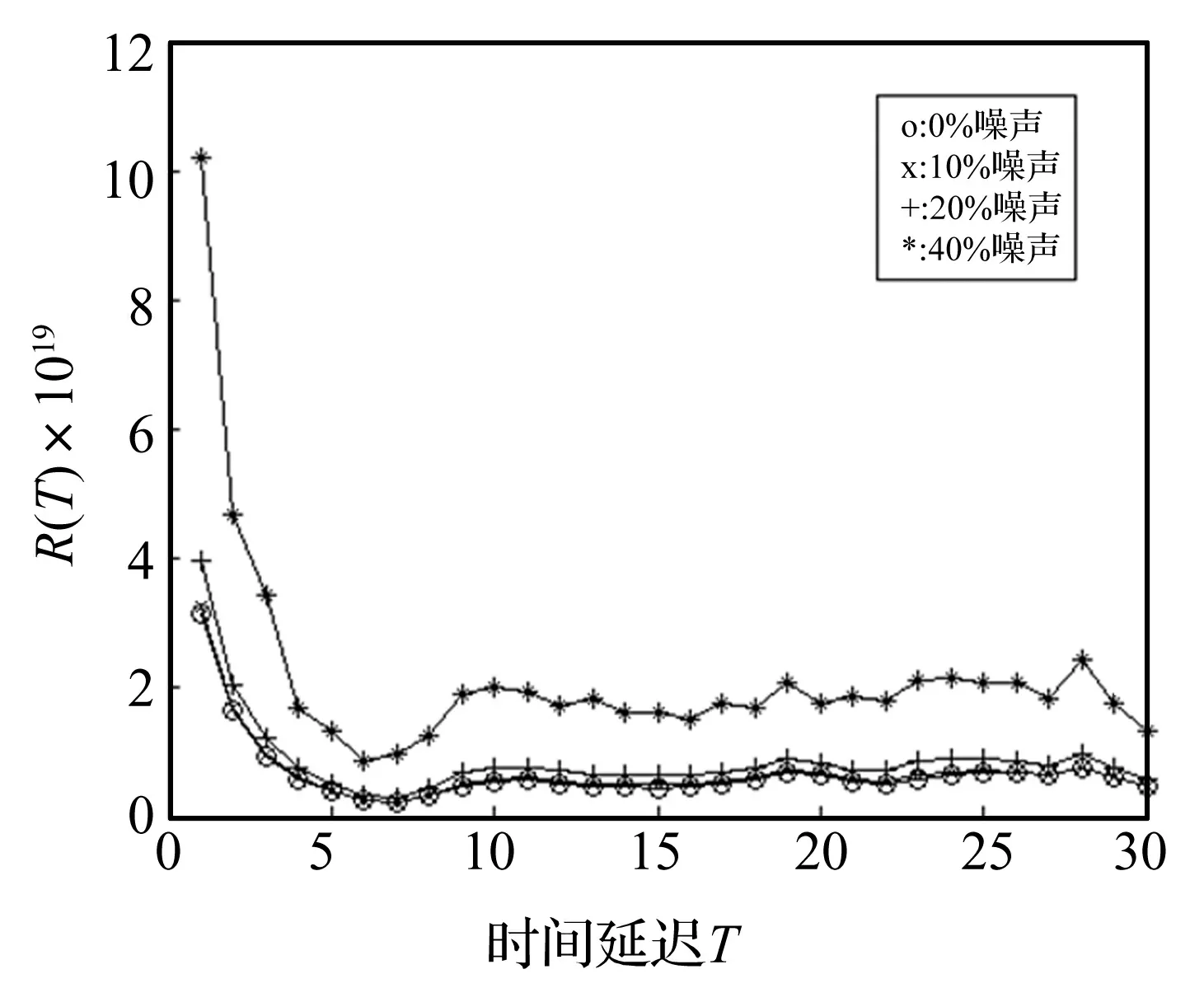
图10 Lorenz系统R(τ)变化关系Fig.10 Nonlinear multiple autocorrelation function of Lorenz
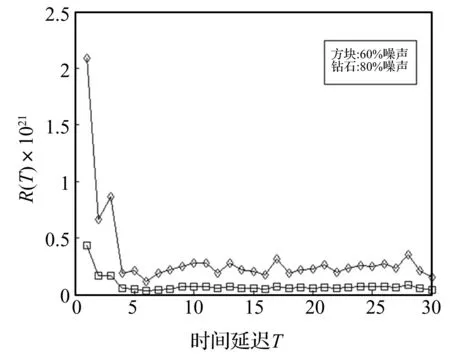
图11 Lorenz系统R(τ)变化关系Fig.11 Nonlinear multiple autocorrelation function of Lorenz
三种方法对不同噪声水平下Lorenz系统的时间延迟计算结果如表5所示,图12是τ=7时x变量的重构吸引子,图13是τ=10时x变量的重构吸引子。对照图3可以看出,虽然时间延迟取7和10都为有效的时间延迟,不过时间延迟为7时的重构吸引子与原吸引子在形状上更加接近。因此,时间延迟取7更合适。
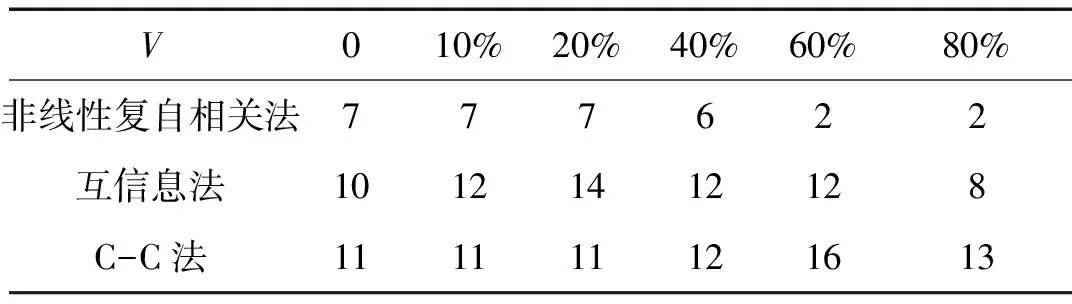
表5 Lorenz系统计算结果

图12 τ=7 Lorenz重构吸引子Fig.12 Reconstructed attractor of Lorenz choosing τ=7
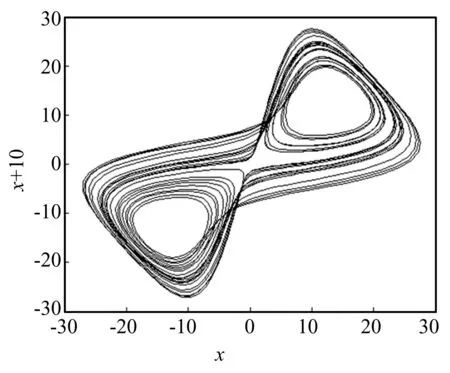
图13 τ=10 Lorenz重构吸引子Fig.13 reconstructed attractor of Lorenz choosing τ=10
4.4 Rossler系统
对Rossler方程

(13)
取a=16,b=2,c=45,初值 (0,0,0),用Runge-Kutta方法求解,去除暂态过程,从中取出2 000个点作为纯净的混沌时间序列。
关联维数d理论值为2.01[15],取嵌入维数m=6计算Rossler系统的时间延迟,图14是R(τ)在不同噪声水平下的变化关系,和前几个系统一样,R(τ)对噪声不敏感。
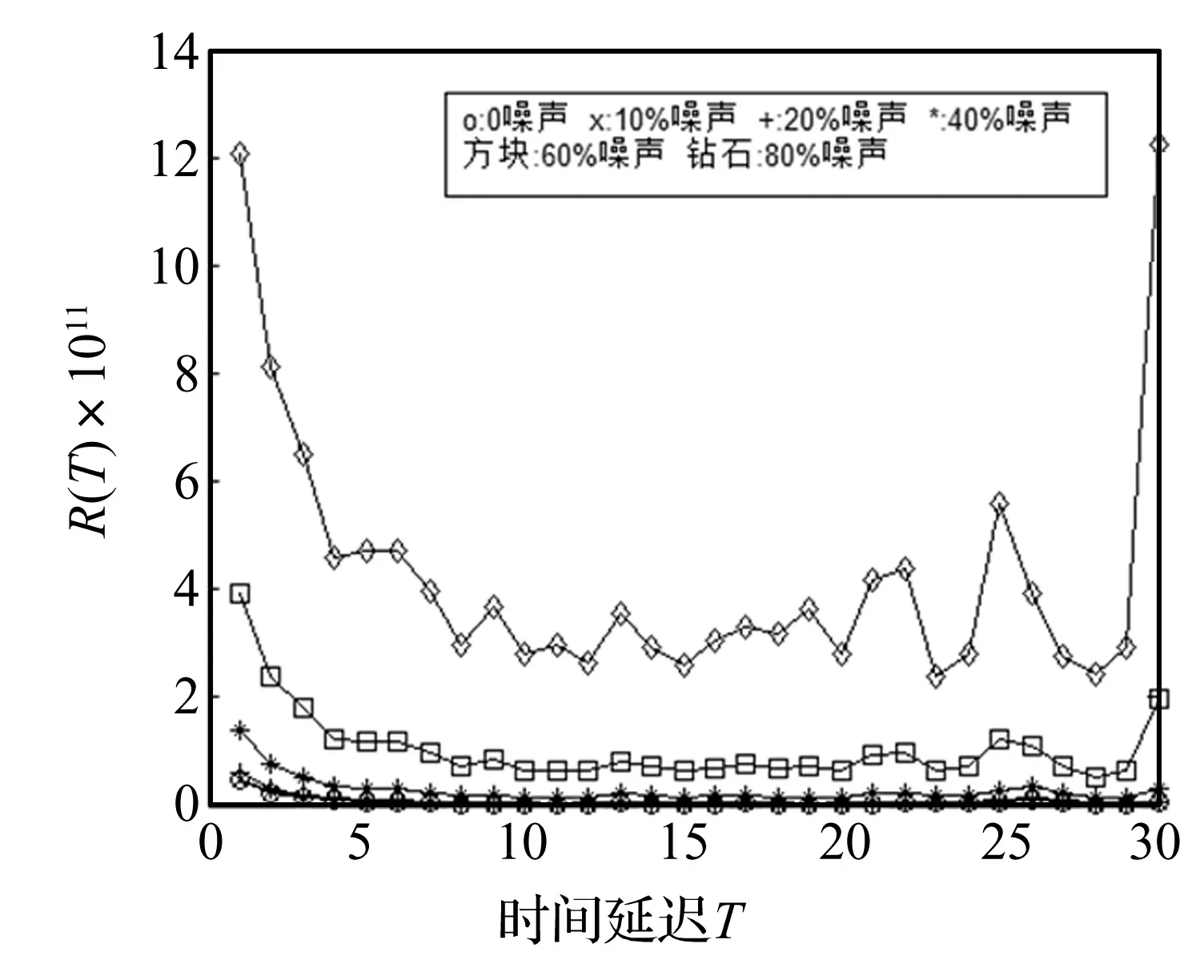
图14 Rossler系统R(τ)变化关系Fig.14 Nonlinear multiple autocorrelation function of Rossler
三种方法对不同噪声水平下Rossler系统的时间延迟计算结果如表6所示,图15是Rossler吸引子在x-y平面上的投影图,图16是τ=11时变量x的重构吸引子,图17是τ=15时变量x的重构吸引子,可以看出时间延迟取11更合适。
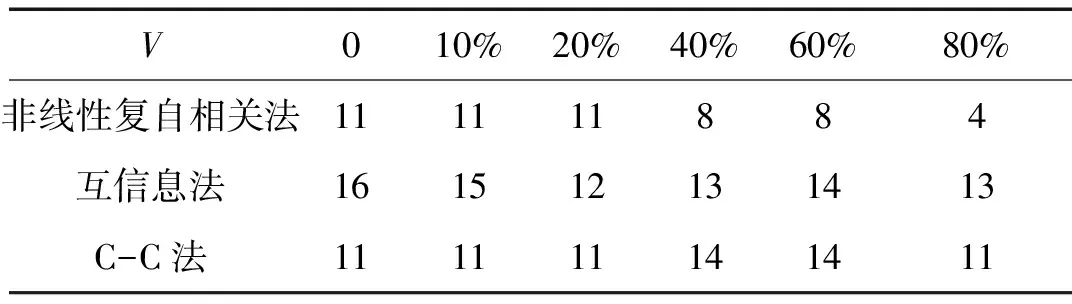
表6 Rossler系统计算结果
4.5 小数据计算
取以上四种混沌时间序列中 (1 901,2 000)区间的数据,嵌入维数取值同上,采用新方法计算各混沌系统的时间延迟,结果如表7所示,与采用2 000数据点时的结果相比,Logistic和Hennon的计算结果与之前相同; Lorenz和Rosser的计算结果在噪声水平小于40%时与之前相同,大于40%时存在一定的偏差。

图15 Rossler吸引子x-y平面投影图Fig.15ProjectionofRosslerstrangeattractoronx-yplane图16 τ=11Rossler重构吸引子Fig.16ReconstructedattractorofRosslerchoosingτ=11图17 τ=15Rossler重构吸引子Fig.17ReconstructedattractorofRosslerchoosingτ=15
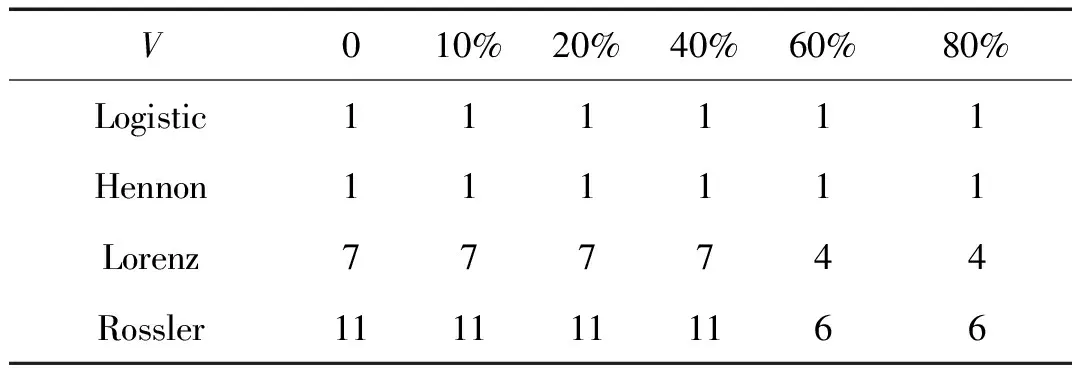
表7 100数据点计算结果
5 结 论
本文提出的非线性复自相关法,通过计算系统的非线性相关性来确定最优时间延迟。从对四种典型混沌动力学系统的计算结果可以看出,与复自相关法、互信息法和C-C法相比,新方法计算出的时间延迟更加合适,同时,在数据量小时的求解结果仍然可靠。该算法所用到的非线性自相关函数R(τ)对噪声不敏感,因此该方法的抗噪声能力也很好。
[ 1 ] Takens F. Detecting strange attractor in turbulence [J]. Lecture Notes in Mathematics, 1981,898(2):366-381.
[ 2 ] Packard N H, Crutchfield J P, Farmer J D, et al. Geometry from a time series [J] . Phys. Rev. Lett., 1980,45(9):712-716.
[ 3 ] Kantz H, Schreiber T. Nonlinear time series analysis[M]. Cambridge: Cambridge University Press, 1997, 127.
[ 4 ] 林嘉宇,王跃科,黄芝平,等. 语音信号相空间重构中时间延迟的选择-复自相关法[J]. 信号处理,1999,15 (3) :220-225. LIN Jia-yu, WANG Yue-ke, HUANG Zhi-ping, et al. Selection of proper time delay in phase space reconstruction of speech signals [J]. Signal Processing, 1999, 15(3):220-225.
[ 5 ] 马红光,李夕海,王国华,等. 相空间重构中嵌入维和时间延迟的选择[J]. 西安交通大学学报,2004,38(4): 335-338. MA Hong-guang, LI Xi-hai, WANG Guo-hua, et al. Selection of embedding dimension and delay time in phase space reconstruction [J]. Journal of Xi’An Jiao Tong University, 2004,38(4):335-338.
[ 6 ] Fraser A M. Information and entropy in strange attractors [J]. IEEE Trans on ITMar,1989, 35(2) :245-262.
[ 7 ] Rossenstein M T, Colins J J, De Luca C J. Reconstruction expansion as a geometry based frame work for choosing proper delay times [J]. Physica : D,1994, 73(1) : 82-98.
[ 8 ] Kugiumtzis D. State space reconstruction parameters in the analysis of chaotic time series-the role of the time window length [J]. Physica : D, 1996,95(1) :13-28.
[ 9 ] Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times and embedding windows [J]. Physica: D, 1999,127 (1) : 48-60.
[10] 陆振波,蔡志明,姜可宇. 基于改进的C-C方法的相空间重构参数选择[J]. 系统仿真学报, 2007, 19(11): 2527-2529. LU Zhen-bo, CAI Zhi-ming, JIANG Ke-yu. Determination of embedding parameters for phase space reconstruction based on improved C-C method [J]. Journal of System Simulation, 2007,19(11):2527-2529.
[11] 秦奕青,蔡卫东,杨炳儒. 非线性时间序列的相空间重构技术研究[J]. 系统仿真学报,2008, 20(11):2969-2973. QIN Yi-qing, CAI Wei-dong, YANG Bing-ru. Research on phase space reconstruction of nonlinear time series [J]. Journal of System simulation, 2008, 20(11):2969-2973.
[12] 符五久. 确定相空间重构参数的一种新方法[J]. 振动与冲击, 2010,29(12): 190-195. FU Wu-jiu. New method for determining parameters of phase space reconstruction [J]. Journal of Vibration and Shock, 2010,29(12):190-195.
[13] 张淑清,贾 健,高 敏,等. 混沌时间序列重构相空间参数选取研究[J]. 物理学报, 2010, 59(3): 1576-1582. ZHANG Shu-qing, JIA Jian, GAO min, et al. Study on parameters determination for reconstructing phase-space in chaos time series [J]. ACTA Physica Sinica, 2010, 59(3):1576-1582.
[14] 张 菁,樊养余,李慧敏,等. 相空间重构中延迟时间选取的新算法[J]. 计算物理, 2011, 28(3): 469-474. ZHANG Jing, FAN Yang-yu, LI Hui-min, et al. An improved algorithm for choosing delay time in phase space reconstruction [J]. Chinese Journal of Computational Physics, 2011, 28(3):469-474.
[15] 姬翠翠,朱 华,江 炜.混沌时间序列关联维数计算中无标度区间识别的新方法[J]. 科学通报, 2010,55(31):3069-3076. JI Cui-cui, ZHU Hua, JIANG Wei. A novel method to identify the scaling region for chaotic time series correlation dimension calculation [J]. Chinese Sci Bull, 2010,55(31):3069-3076.
[16] 韩 敏. 混沌时间序列预测理论与方法[M]. 北京:中国水利水电出版社, 2007,92.
[17] Nichols J M, Nichols J D. Attractor reconstruction for non-linear systems: a methodological note [J]. Mathematical Biosciences, 2001, 171(1): 21-32.
[18] Aguirre L A. A nonlinear correlation function for selecting the delay time in dynamical reconstructions [J]. Physics Letter A, 1995, 203(2-3):88-94.
[19] 王 军,石炎福,余华瑞. 相空间重构中最优滞时的确定[J]. 四川大学学报:工程科学版,2001,33(2):47-51. WANG Jun, SHI Yan-fu, YU Hua-rui. Determination of optimal delay time in reconstructing phase space [J]. Journal of Sichuan University( Engineering Science Edition)2001,33(2):47-51.
[20] 梁学章,张 明,张洁琳,等. 高维空间中代数流形上多项式空间的维数与Lagrange插值适定结点组的构造[J].吉林大学学报:理学版,2006,44(3):309-317. LIANG Xue-zhang, ZHANG Ming, ZHANG Jie-lin, et al. The dimension of polynomial space and the construction of properly posed set of nodes for Lagrange interpolation on algebraic manifold[J]. Journal of Jinlin University: science edition, 2006,44(3):309-317.
Time-delay estimation for phase space reconstruction based on detecting nonlinear correlation of a system
XU Yan1,2, WANG Bo1, LI Peng3
(1. College of Computer Science, Chongqing University, Chongqing 400044, China;2. Xichang Satellite Launch Center, Xichang 615000, China;3. The 38thResearch Institute, China Electronic Technology Group Corporation, Hefei 230051, China)
A new method to determine time-delay was proposed, it was called nonlinear multi-autocorrelation function method. With this method a high order multi-autocorrelation functionR(τ) was used to calculate the nonlinear correlation of a system and estimate the optimal time delay by finding the first local minimum value ofR(τ). The time complexity ofR(τ) was low and its dependence on the length of data was not strong. The method was validated with four noisy chaotic time series. The time series were generated using four chaotic maps inputting Gaussian white noise with different levels. The numerical results showed that the proposed method is more appropriate with a good anti-noise ability.
chaotic time series; noise level; phase space reconstruction; embedded dimension; time delay
2013-01-10 修改稿收到日期:2013-06-04
许岩 男,硕士生,1982年生
TN751
A
10.13465/j.cnki.jvs.2014.08.002

