数控机床进给伺服系统研究进展

吴子英， 刘宏昭， 王 胜， 刘丽兰

(西安理工大学 机械与精密仪器工程学院, 西安 710048)

数控机床进给伺服系统研究进展

吴子英， 刘宏昭， 王 胜， 刘丽兰

(西安理工大学 机械与精密仪器工程学院, 西安 710048)

针对目前数控机床进给系统的发展状况，首先描述了进给系统的几种结构形式，分析了不同结构形式的特点及适用场合。然后介绍了进给系统运动性能的预测及检测方法。并且系统地阐述了几种进给系统力学模型及其特点，分析了进给系统中影响进给系统动态性能的非线性因素，详细论述了多种摩擦和间隙控制补偿方案及其各自特点。最后，针对当前进给系统建模及控制方面存在的不足提出了几点展望，为今后进给系统的相关研究提供了参考。

进给伺服系统; 传动结构; 性能预测; 力学建模; 控制补偿

随着科学技术的日益发展，精密和超精密加工技术已经成为机械加工领域重要的研究方向，而实现高精度加工的首要条件就是要具有高精度的数控加工设备。进给伺服系统作为各种数控设备的核心组成部分，是一种精密的位置跟踪与定位系统，其运动精度和定位精度直接关系到数控系统的加工精度、产品表面质量和生产效率。

为了满足不同产品的数控加工，对进给系统的要求也大不相同，如快速加工的高速进给[1]、精加工的低速进给[2]、超精密加工的纳米进给[3]及低速纳米组合进给[4]等，这就导致了在进给系统的结构设计、驱动形式及控制方案的具体选择上存在较大差别，不同结构形式中非线性因素的起作用方式也均不同。因而，本文将从进给系统的机械结构、驱动方式、控制方案、精度检测、力学建模及控制补偿方案几个方面系统地论述目前相关的研究现状，并针对存在的问题提出若干建议。

1 进给系统传动结构

为了实现进给系统的合理功能，通常根据其工作场合、负载大小、定位精度、运动方式进行传动结构设计及导轨选择。

1.1 直连型

中小型数控机床和教学实验型进给系统通常采用伺服电机直连滚珠丝杠型的结构形式，如图1所示。伺服电机通过联轴器直接驱动滚珠丝杠，丝杠通过螺母带动工作台，将伺服电机的旋转运动转换成工作台的直线运动。

图1 直连式进给伺服系统结构简图Fig.1 Schematic of the direct-connected feed servo system

直连式进给系统主要特点如下：

(1)结构特点：省略齿轮箱等中间传动链，提高了传动效率和控制精度；

(2)控制方式：半闭环或者闭环控制；

(3)导轨类型：滑动导轨(多进行贴塑处理)、滚动导轨和静压导轨；

(4)精度等级：根据工作台输出精度选择滚珠丝杠精度的精度等级；

(5)丝杠导程：中低速采用中等导程，对于高速运动采用大导程；

(6)间隙处理：常采用双螺母结构，利用两个螺母的相对轴向位移消除间隙；

(7)负载大小：中小型负载。

1.2 含齿轮箱型

此种传动类型多见于重型数控机床上，通常采用齿轮箱来增大伺服电机的输出转矩，如图2所示的某重型车床的横向进给系统简图[5]。在控制指令下，电机转动驱动齿轮箱，齿轮箱用于提高传动轴的转矩，从动齿轮再带动滚珠丝杆旋转，最后由滚珠丝杠将回转运动转化为工作台的直线运动。

含齿轮箱式进给系统主要特点如下：

(1)结构特点：引入齿轮箱，增大了电机输出扭矩；

(2)控制方式：多采用闭环控制以消除传动链引入的传动误差；

(3)导轨类型：少数采用滑动导轨(贴塑处理)，多数采用静压导轨。

(4)精度等级：常采用大直径中等精度的滚珠丝杠；

(5)丝杠导程：导程通常16 mm以下;

(6)间隙处理：采用斜齿轮消隙，如图3所示，两个斜齿轮中间装有垫片，通过调整中间垫片的厚度消除齿轮侧隙；

(7) 负载大小：适用于重型负载；

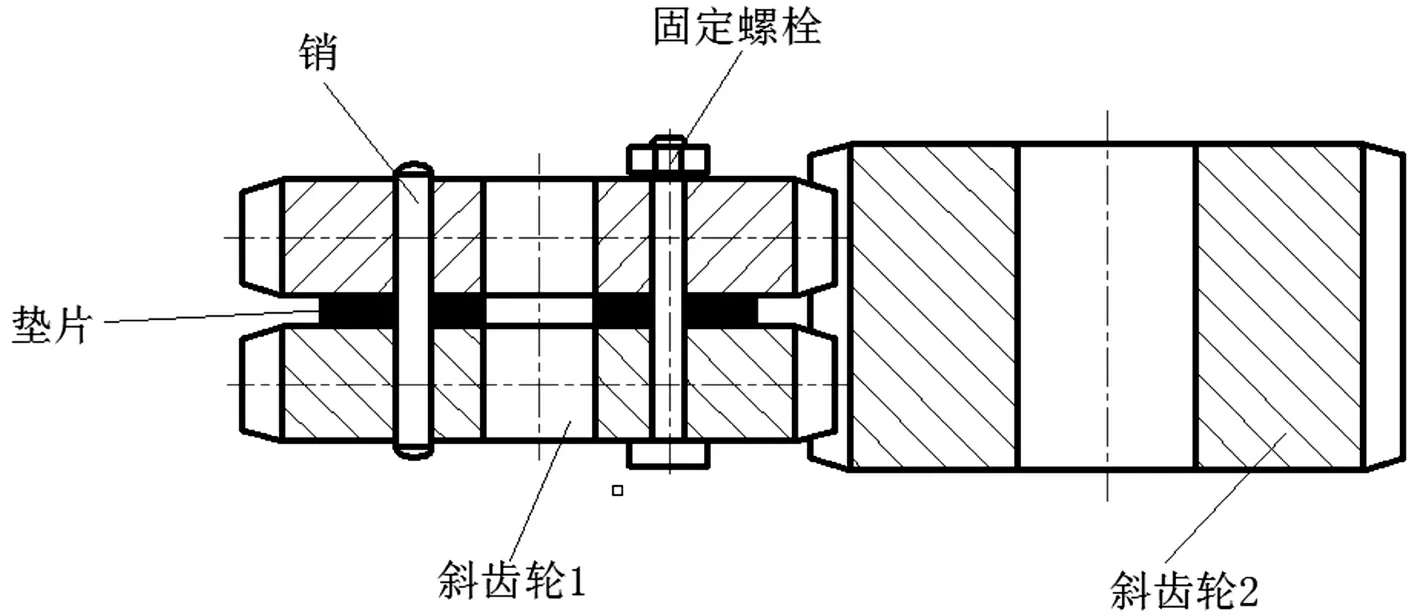
图3 斜齿轮垫片消隙简图Fig.3 Elimination of the helical gear meshing backlash using gasket

1.3 直线电机型

直线电机是一种将电能直接转换成直线运动机械能而不需要任何中间转换机构的传动装置。由于其传动链最短，性能优越，常用于高速进给伺服系统，同时也适用于低速、小负载进给场合。

直线电机型进给系统主要特点如下：

(1)结构特点：电机不需要经过中间转换机构而直接产生直线运动，使结构大大简化；

(2)控制方式：闭环控制；

(3)导轨类型：滚动导轨应用较多；

(4)精度等级：省去了中间运动转换环节，动态响应性能和定位精度大大提高；

(5)负载大小：中小型负载；

1.4齿轮齿条型

该型进给系统通常用于重型数控机床的纵向进给系统，以满足大型工件纵向加工的需要，通常将斜齿条固定在床身上，伺服电机及齿轮箱安装在纵向进给系统上，如图4所示某重型数控车床的纵向进给系统简图[6]。在加工过程中，为了使导轨两侧的作用力均布，也可采用流体静压蜗杆—蜗母牙条传动，将蜗母牙条放置在机床两侧导轨中间，实现了两侧导轨作用力均衡，如图5所示。

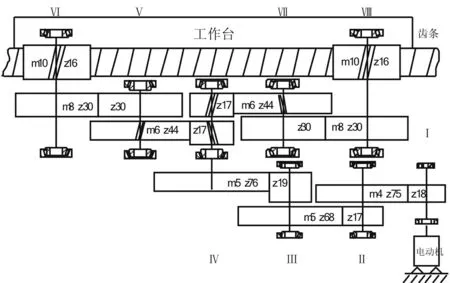
图4 某重型车床纵向进给系统简图Fig.4 Schematic of the longitudinal feed system of a heavy duty lathe

图5 蜗杆—蜗母牙条传动实物图Fig.5 The physical worm and gear drive system

齿轮齿条型进给系统主要特点如下：

(1)结构特点：实现了工作台长距离进给的需要；

(2)控制方式：多采用闭环控制以消除传动链引入的传动误差；

(3)导轨类型：少数采用滑动导轨(贴塑处理)，多数采用静压导轨；

(4)精度等级：通常取决于齿轮的加工精度；

(5)间隙处理：原理如图6所示，为了减少齿轮传动带来的传动误差，部分重型数控除去了图4中的多级齿轮减速，改装成两个大功率交流伺服电机分别直接驱动两个小齿轮，通过控制输出力矩的大小消除纵向进给系统往复运动产生的间隙；

(6)负载大小：适用于重型负载；

图6 齿轮齿条传动消隙原理图Fig.6 Elimination of the gear and rack transmission backlash

2 进给系统运动性能预测及检测

数控机床制造完成以后，需采用光学仪器进行几何精度、运动精度等方面的检测。为了提高数控机床的运行可靠性和精度可靠性，国家开展了针对数控机床的科技重大专项项目研究，本文作者参与了西安交通大学主持的《国产高档数控机床与基础装备研究》项

目的研究工作，主要负责数控机床进给伺服系统的动态特性和精度可靠性方面的研究，取得了相关研究成果。

2.1 传动精度影响因素分析

宋江波等[6]从机械精度设计理论和机械可靠性设计理论出发，建立了某重型数控车床纵向进给系统(如图2所示)精度可靠性的模型，分析了影响数控机床传动精度的主要因素。

在综合考虑切向综合误差(几何偏心、运动偏心、基节偏差和齿廓偏差)、齿距累积误差、齿轮径向跳动、公法线长度变动、轴的径向跳动、齿轮与轴的配合间隙、滚动轴承内外圈径向跳动这七个影响因素的作用下，假设各个误差项都是符合正态分布，建立一对齿轮传动的角值传动误差的均值μ1,2和标准差σ1,2的数学模型：

μ1,2=0

(1)

式中各符号含义详见参考文献[6]。

通过计算分析出七个因素对齿轮传动精度重要程度的大小，再利用灵敏度设计理论按照对影响传动精度因素的重要度进行排序，找出精度可靠性的薄弱环节，计算结果如表1所示。可知，对传动精度影响最大的因素是切向综合误差。切向综合误差是在接近齿轮的工作状态下测量的，包括几何偏心、运动偏心、基节偏差和齿廓偏差的综合测量结果，是评定齿轮传动准确性的首选指标。

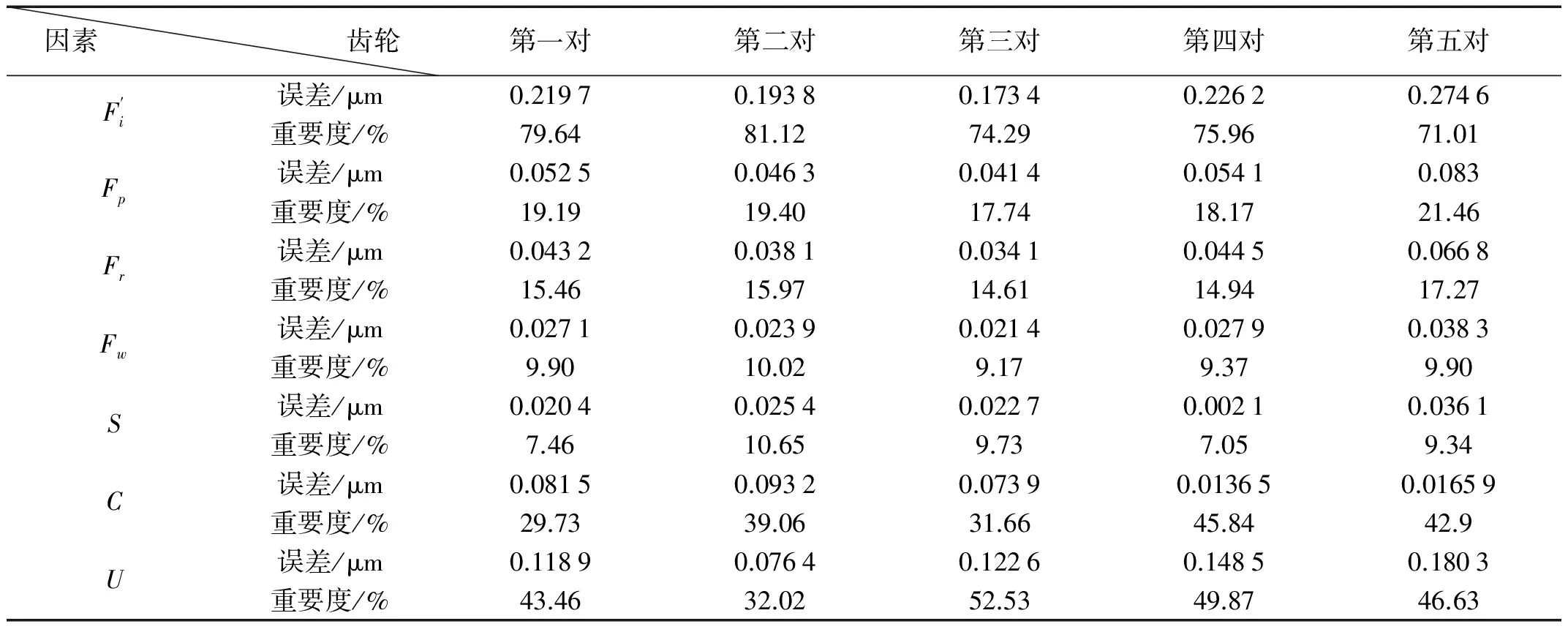
表1 各对齿轮误差项对传动误差的影响

2.2 定位精度预测

为了能够准确快速地评估重型数控车床的定位精度，王胜等[7]在分析重型数控车床定位精度的激光测量原理和方法的基础上，提出了基于全域数据的BP 神经网络和RBF 神经网络的进给系统定位精度预测方法，并对某车床Z 轴方向的定位精度进行了实地测量，通过采用两种神经网络方法对实验数据进行分析得到了目标位置点的定位精度。其中B段和C段定位精度的预测值相对误差曲线如图7和图8所示。

分析结果表明，RBF神经网络预测精度优于BP神经网络，同时由预测结果也可以发现，远程预测的误差相对较大，如何得到更为精确的远程预测结果仍需进一步研究。

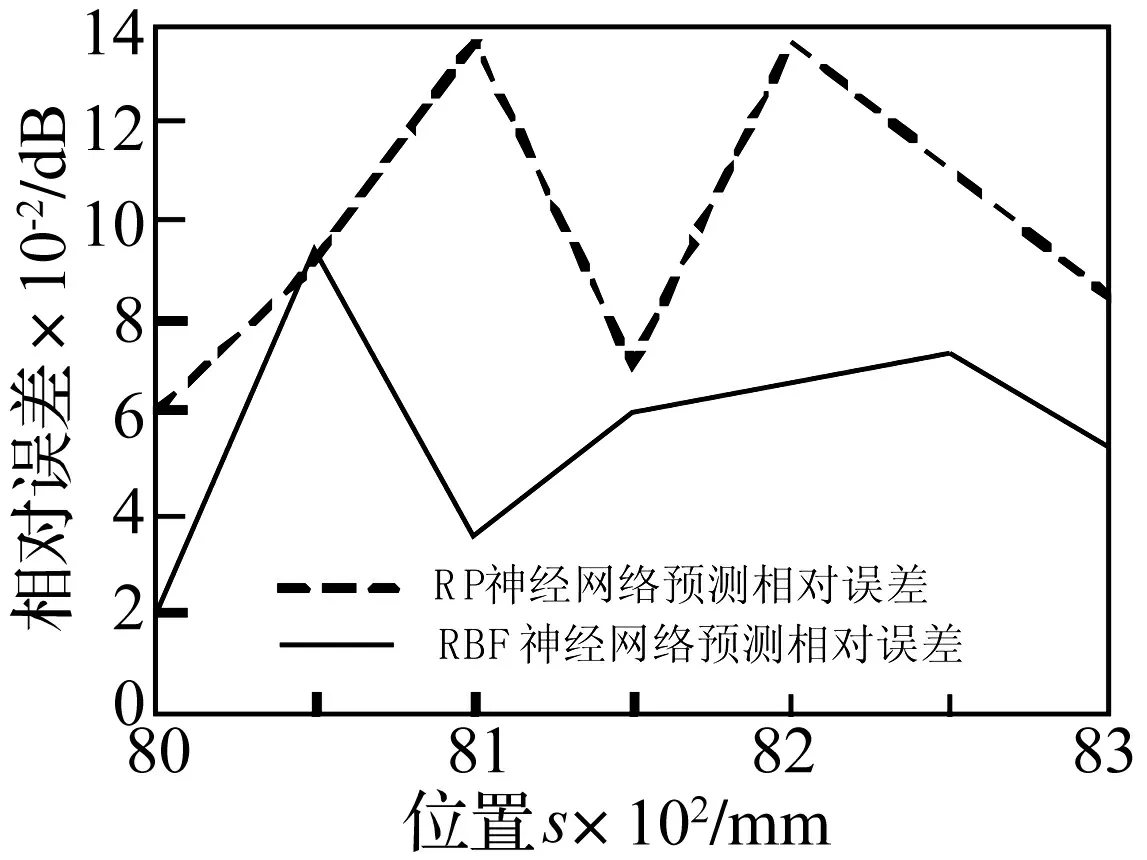
图7 B段测点相对误差曲线Fig.7 Relative error curve of B section

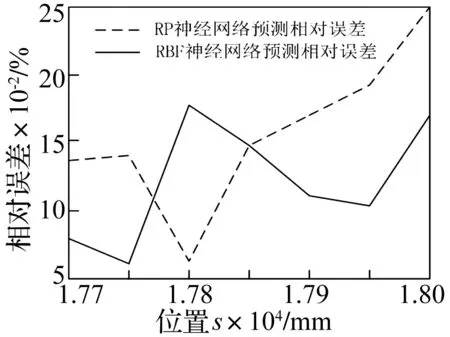
图8 C段测点相对误差曲线Fig.8 Relative error curve of C section

2.3 工作台爬行运动检测

针对进给系统工作台在低速运行较易发生爬行运动的问题，吴子英等[8]以图2所示的横向进给系统为研究对象进行了爬行运动检测。该型号数控机床的横向进给系统及测试装置见图9。

滚珠丝杠总长1.773 m，采用两端止推的支撑方式。工作台运行过程中为滑动摩擦，行程为1 000 mm，测试共取了8个位置作为测点。测试过程中车床主轴停止转动，横向进给系统空载运行，测量各点临界爬行速度。通过测试获得横向进给系统工作台的临界爬行速度、丝杠综合传动刚度与工作台位置之间的关系曲线，如图10所示。

图9 横向进给系统及Renishaw测试系统Fig.9 Cross feed system and the Renishaw test system

从图10可以看出，在8个测点处由于工作台在运行中处于丝杠的不同位置，因此每一测点的刚度是不同的。传动刚度由丝杠两端向丝杠中间位置逐渐减小。且传动刚度增大，临界爬行速度趋于减小。因此可以判断是传动刚度的变化导致了工作台临界爬行速度的变化。在刚度最大的位置，临界爬行速度最低，有利于系统稳定。

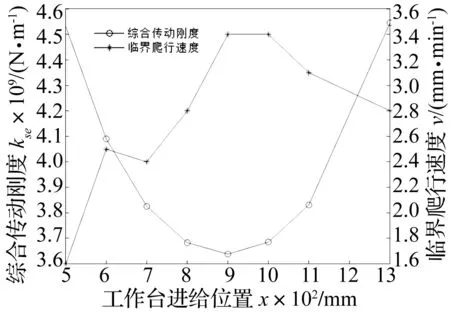
图10 临界爬行速度、综合传动刚度与工作台进给位置的关系Fig.10 The relationship curves among the critical stick slip velocity, the comprehensive transmission stiffness and the feed position

2.4 数控机床实时监测

随着对数控机床可靠性要求的不断提高，通过实时监测数控机床关键部件的实时运行数据，以预测机床运行状态的发展趋势，为数控机床维护提供指导依据成为了一个亟待解决的问题。

周玉清等[9-10]借助ePS系统读取数控机床本体根植的内置传感器，通过自主开发测试系统，结合国外伺服系统(如Siemens等)的硬件信息，在无需借助外部仪器的情况下，直接读取数控机床内置检测元件的数据信息，提出一种基于光栅尺、编码器、伺服进给电机电流(转矩)内置传感器的机床状态监测系统，达到了对数控机床各部件(如伺服电机输出转矩、电流、工作台位置、瞬时速度、瞬时加速度等)不同工况下性能的实时检测，为数控机床部件的状态监测和故障诊断提供了技术支持，获得了社会认可[9]。

3 进给系统力学建模

进给系统的性能对数控机床的轨迹跟踪、定位精度及加工表面质量等均有着重要的作用，评估其性能好坏，往往是通过建立合理的力学模型对其性能进行预测和分析的。由于分析对象的结构及分析目的的不同，建立的力学模型也有所不同。通常可简化为如下三种类型：单自由度系统、两自由度系统和多自由度系统。

3.1 单自由度模型

进给系统单自由度模型是最简单的力学简化模型。将进给伺服系统的转动部分向工作台移动部件等效，使之成为一个单自由度系统，如图11所示。

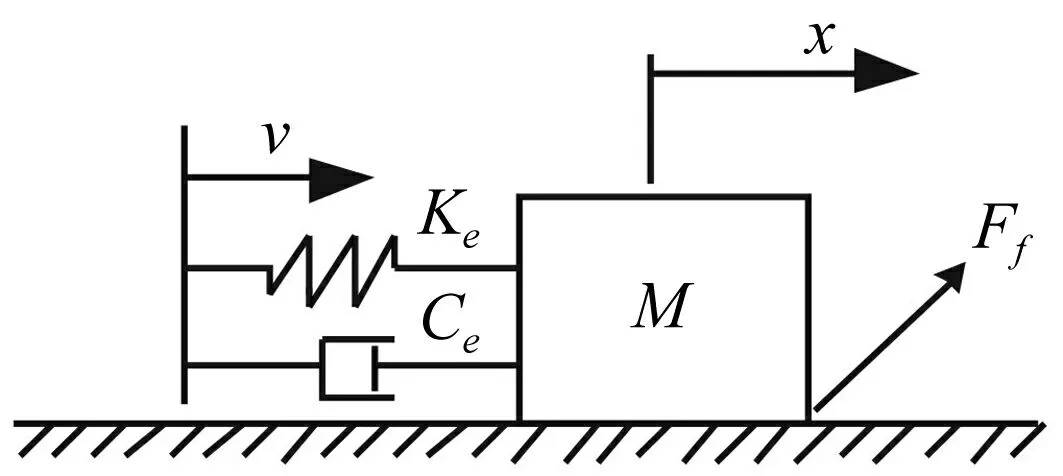
图11 单自由度系统力学模型Fig.11 SDOF mechanical model

在假设驱动速度为常数的情况下，根据参考文献[11]可得到质量块M发生爬行运动时的临界驱动速度表达式为

(3)

式(3)中各符号含义详见参考文献[11]。

该单自由度力学模型常用于进给系统临界爬行速度计算[12]、多传动链系统的刚度分析[8]及控制系统稳定性分析[2]。

优点：模型简单明了，简化了工程计算量，适用于各类驱动系统，如机床导轨类、气动、液压系统中存在摩擦时的爬行现象分析；结合Routh判据进行控制系统分析时，实现简单，能够很容易的分析出控制参数的变化范围。参考文献[2]将图1所示的进给系统简化为单自由度系统，借助Routh判据进行了该系统的PID稳定性研究，仿真和实验均取得了很好的效果。

不足：当较为复杂的、含传动链的系统出现爬行时，无法更加具体描述中间环节的工作状态和动态响应，从而找出系统的问题所在，分析细节问题较为笼统。

3.2 两自由度模型

刘丽兰等[13]在分析摩擦和间隙对进给系统输出行为的影响时，建立了两自由度简化力学模型，如图12所示。

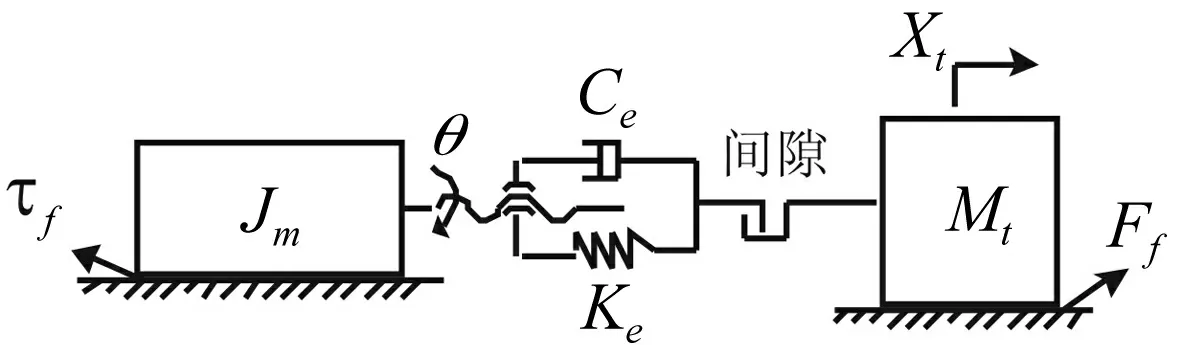
图12 两自由度系统力学模型Fig.12 2-DOF mechanical model

该力学模型也可用于分析闭环控制的进给系统转动和传动部分的参数匹配关系及传动非线性因素的的影响规律。该系统的动力学方程为

(4)

式(4)中各符号含义详见参考文献[13]。

优点：模型能够较为全面的描述进给系统，可适用于具有中间传动链的进给系统，如数控机床的纵向、横向进给系统、气动、液压伺服驱动系统；模型物理意义明确、易于理解、计算量较小，与控制系统结合紧密，借助Simulink仿真软件，可与各类控制补偿方案有机结合。

不足：实际进给伺服系统是连续系统，在简化过程中存在对实际系统的较多忽略和简化，在一定程度上弱化了系统中真实存在的现象，对于传动关系复杂的进给伺服类机电系统，仍无法描述具体某一中间环节的工作状态及对工作台输出的影响。

3.3 多自由度系统

对于复杂的、传动链较长的进给系统，为了便于对该类系统进行结构改进及优化，建立能够体现多环节作用的多自由度系统十分必要。

[14]以一个含有带传动、滚珠丝杠传动的进给伺服系统为研究对象，建立了带轮、带、丝杠的多自由度力学模型，并分析了该进给系统各部分刚度的贡献，最后针对摩擦和间隙两个非线性因素进行了数值仿真及实验研究。

吴子英等[5]以图2所示的进给系统为研究对象，建立了考虑中间各传动环节的系统多自由度力学模型，如图13所示。

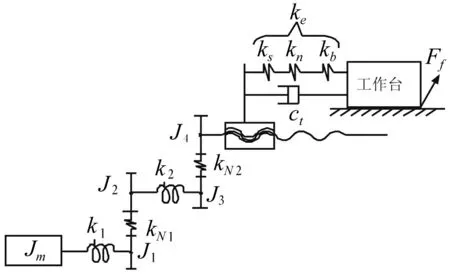
图13 多自由度系统力学模型Fig.13 MDOF mechanical model

根据力学模型，系统的动力学方程为:

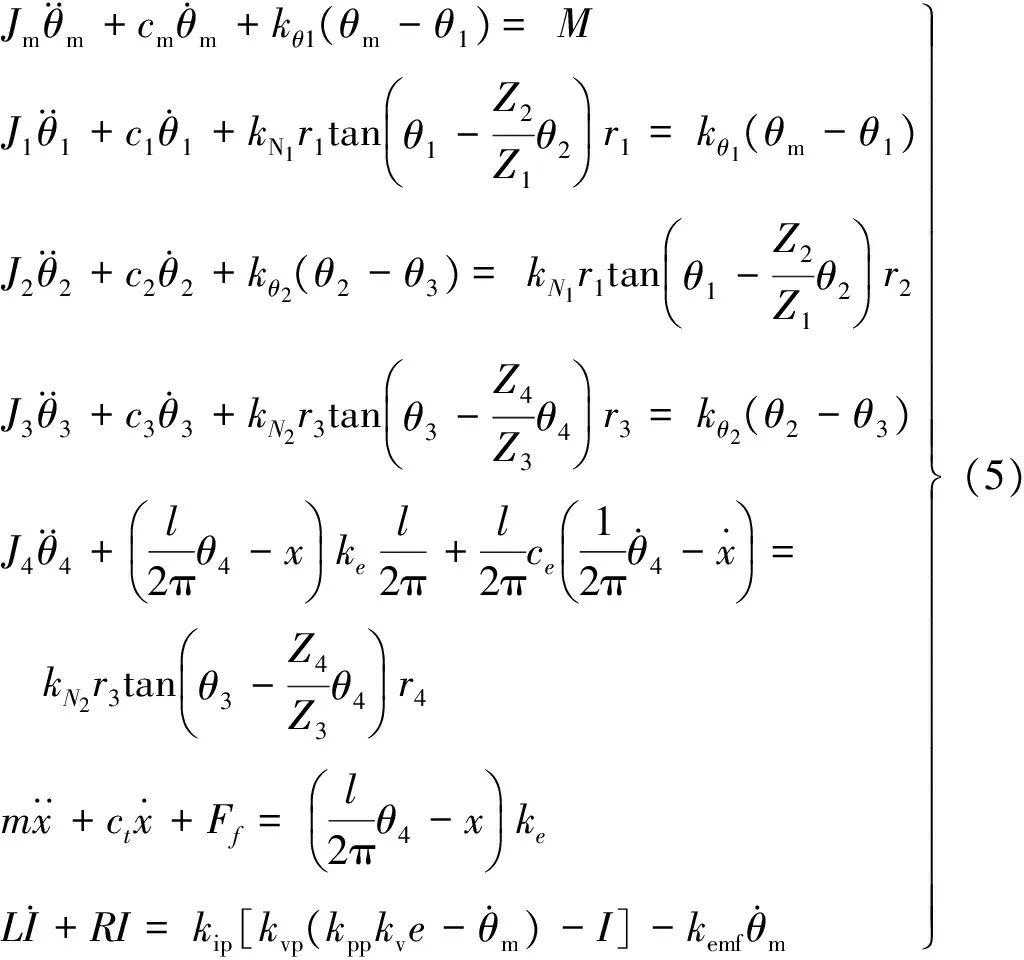
优点：多自由度力学模型能够较为全面的描述进给系统的中间传动环节，如各轴扭转刚度、齿轮啮合刚度等，可观测出各轴动态响应及对工作台输出的贡献。适用于含各种机械传动链的、较为复杂的进给系统或者机电伺服系统

不足：计算量明显加大。在各环节中阻尼是一个非常重要的结构参数，难于确定，文献[5]中各个子系统中阻尼采用了简化的确定方式，直接影响到了理论模型逼近实际模型的程度。在稳定性方面，由于系统自由度多，如再采用Routh判据进行稳定性分析，则会导致多项式的阶次过高，运算量极度膨胀，所以判断稳定性时，可采用其它稳定性理论。

4 典型非线性因素及控制补偿

在进给伺服系统中存在的典型非线性因素主要有滑动导轨处的摩擦和运动副间隙，二者对进给系统动态输出行为均具有重要的影响。

4.1 摩擦因素

存在于进给系统运动副处的非线性摩擦是影响进给定位精度和跟踪精度的主要因素。摩擦可引起极限环振荡、跟踪误差以及爬行运动等。在低速运动及速度换向时，摩擦的作用尤为显著。在众多已建立的摩擦模型中，LuGre模型是一个比较完善的摩擦模型，能够准确地预测摩擦的各种重要特性，而且其对摩擦环节的动态补偿效果较好，已被广泛应用在高精度机械系统的控制中[15]。

LuGre模型的数学表达式为

(6)

(7)

(8)

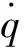
在有关该模型的参数辨识及基于该模型控制补偿方面，国内外学者做了大量工作。如向红标等[16]针对开放式伺服系统，采用Backstepping方法设计自适应摩擦补偿控制器，提出一种基于LuGre模型的自适应摩擦补偿方法；于伟等[17]等对光学精密转台进行基于LuGre模型控制补偿；Chen等[18]以XY直线运动平台为对象，提出了基于LuGre模型的自适应扰动观测器等。

4.2 间隙因素

在机械系统中，为了保证两构件能相对运动，运动副间隙是不可避免的，传动间隙的存在可能导致机构的运动学和动力学特性发生变化。

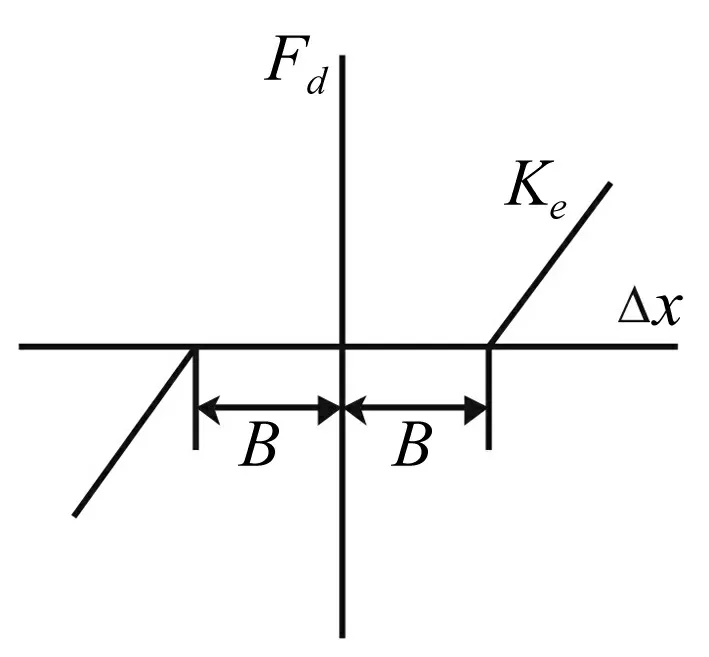
图14 间隙非线性Fig.14 Schematic of nonlinear backlash

对于进给系统来讲，间隙主要是指丝杠和螺母副之间的间隙或齿轮的啮合间隙，由于间隙的存在，系统驱动力Fd将发生变化，假设刚度Ke在间隙区间内为零，间隙非线性特性如图14所示。

参考文献[19-20]主要研究了丝杠螺母副中的间隙，并进行了间隙的控制补偿工作。而文献[13]借助Simulink软件研究了低速进给条件下摩擦和间隙非线性对工作台输出的影响，分析得出了间隙虽不是导致爬行的直接原因，却会令系统在较低的静动摩擦力比值下发生爬行的结论。

4.3 控制补偿方案

近年来，针对机构中摩擦和间隙的研究主要集中在运动控制领域，采用控制补偿方法以解决进给系统中二者引发的定位误差、轨迹跟踪误差等问题。补偿的方法类型较多，如PID控制、神经网络控制、滑模变结构控制、自适应控制等。

(1) PID控制

参考文献[2]将数控机床的进给系统简化为单自由度系统，利用经典的PID控制研究了低速进给时非线性摩擦对系统稳定性的影响，如图15所示。

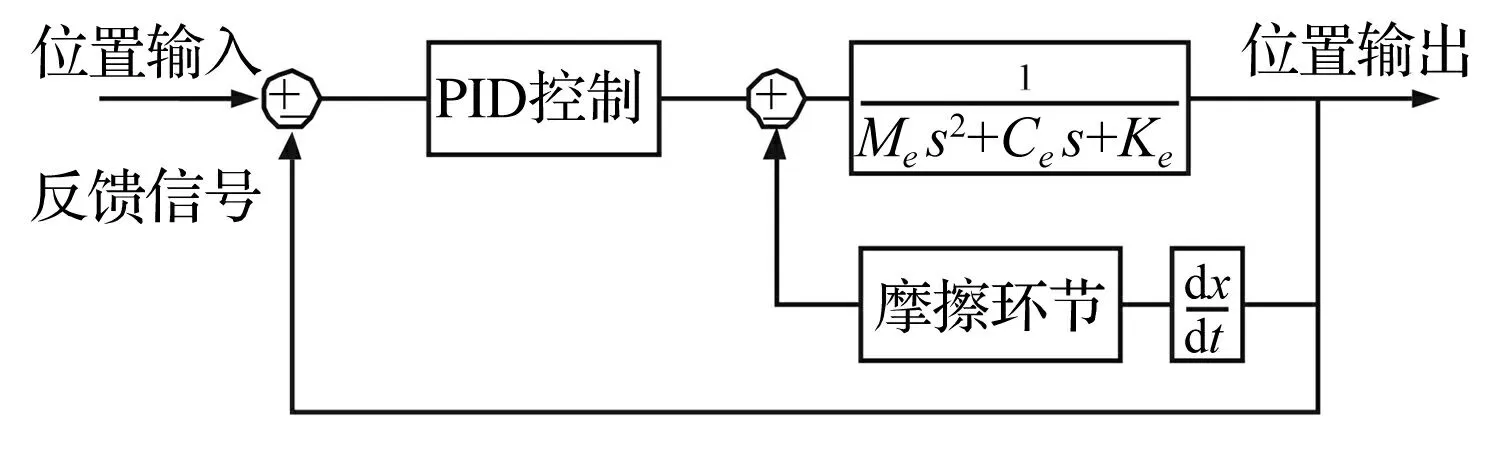
图15 进给伺服系统PID控制框图Fig.15 PID control Schematic of fee servo system

图15所示的PID控制是常规控制方法，但因含有积分环节，导致系统响应从静止到稳态的过渡过程中会产生超调(或振荡)，这会使进给系统的加工精度受到不利影响。

特点：基于误差的控制方法，控制原理简单且易于实现。随着相关学科的发展，自适应PID控制、智能PID控制、模糊PID控制、神经网络PID控制等控制理论相继出现[21]。

(2) 摩擦前馈补偿

前馈摩擦补偿方法是通过对进给系统中的摩擦环节建立适当的数学模型，然后由模型和系统的状态变量信息对摩擦力矩进行估计和补偿，最终消除摩擦环节对系统的影响。由于工况多变，会导致前馈补偿方法不能精确反映摩擦现象的本质，从而引入控制误差。

参考文献[22]为了弥补前馈摩擦补偿的不足，首先采用卡尔曼滤波来辨识系统的位置、速度和扰动，然后利用带极点配置的反馈控制器消除摩擦、切削力及驱动参数变化的影响，以组合前馈补偿的方式消除摩擦等非线性因素的影响，其控制补偿方案如图16所示。

图16 前馈补偿控制方案Fig.16 Control scheme of feed forward compensation

(3) 双环控制补偿

参考文献[23]提出双速度控制器进行非线性摩擦补偿，该控制器分为外部的速度控制器和内部的摩擦力矩补偿器，摩擦力矩补偿器中增加了额外的与伺服系统中摩擦力矩相对应的摩擦力矩，从而使工作台的实际速度能够快速的跟踪参考信号，其控制补偿方案如图17所示。

图17 双速度控制补偿方案Fig.17 Control scheme of dual speed control

(4)自适应控制

针对摩擦前馈补偿的不足，自适应控制无需对进给系统中摩擦模型参数准确辨识，且在摩擦参数随着负载的变化而变化的情况下，通过在线辩识和控制以后，控制系统逐渐适应，最终将自身调整到一个满意的工作状态。

参考文献[18]综合各个补偿器的优点，将前馈摩擦补偿、反馈控制、扰动控制及自适应控制集成在一起，得到了自适应扰动补偿器，如图18所示。

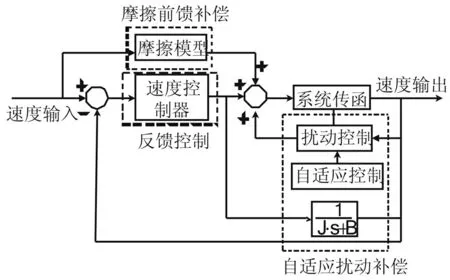
图18 自适应扰动补偿方案图Fig.18 Control scheme of adaptive disturbance control

(5) 滑模控制

滑模控制也叫变结构控制，本质上是一类特殊的非线性控制，可以在动态过程中，根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动。其优点是能够克服系统的不确定性, 适用于进给系统中摩擦力的多变性，鲁棒性强。

参考文献[24]对含间隙和摩擦的闭环控制的电机滚珠丝杠系统进行研究，将再现小波神经网络嵌入到滑模控制器中，其中间隙采用了与输入信号特性相关的非线性模型，并采用三层再现小波神经网络进行近似，该文献同时对摩擦和间隙进行了控制补偿，其控制补偿方案如图19所示。

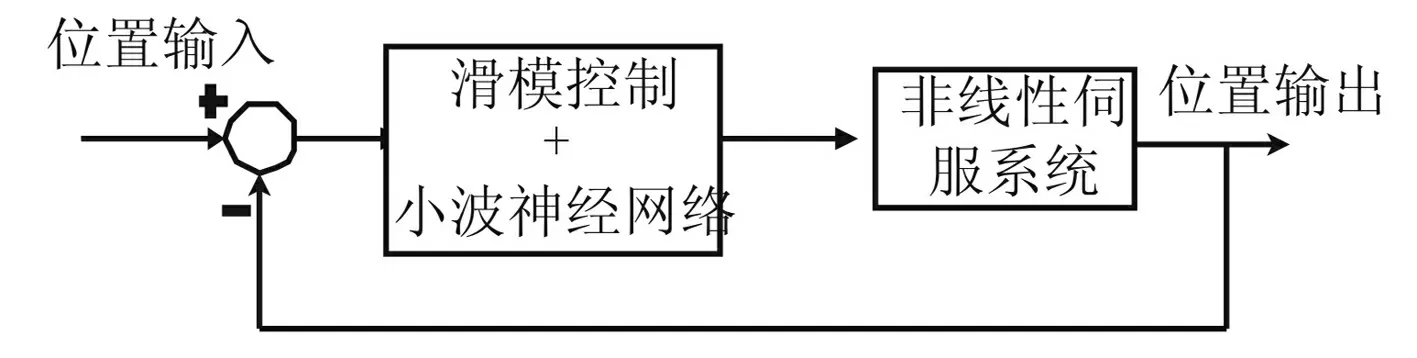
图19 滑模结合再现神经网络控制补偿方案Fig.19 Sliding mode control coupling with recurrent neural network control

(6) 模糊控制

传统的控制理论对于明确系统有很强的控制能力，但对于过于复杂或难以精确描述的系统，则显得无能为力。而模糊控制是利用模糊数学的基本思想和理论的控制方法，适合于复杂的、变量多的进给伺服系统。参考文献[25]以使用Siemens伺服驱动系统的直线电机进给系统为对象，建立了绕组电流和切削力的数学模型，以电流作为反馈控制量，采用模糊控制作为控制方案，如图20所示。

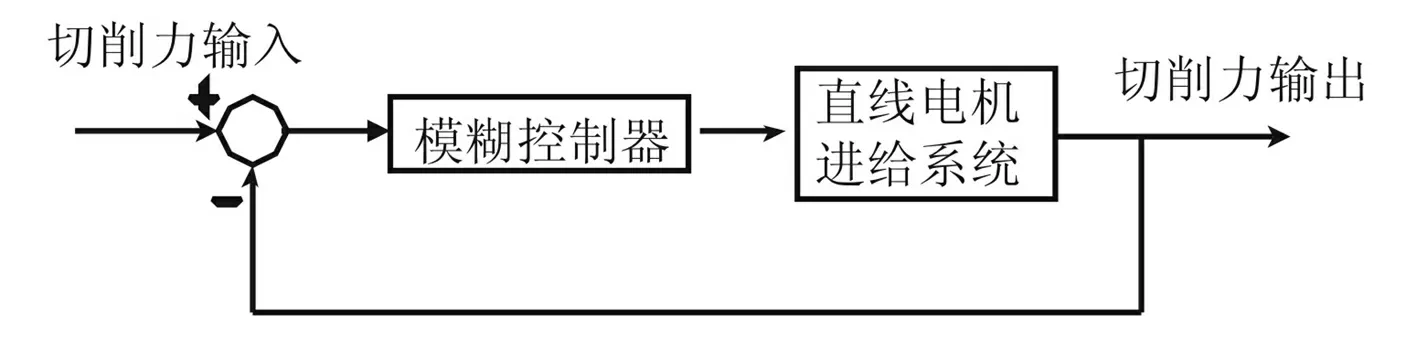
图20 模糊控制方案Fig.20 Control scheme of fuzzy control

总的来看，在进给系统的控制补偿方面的研究工作较多，控制方案各异，各有千秋，在一定程度上已取得了较好的摩擦控制补偿效果。但无论是自适应滑模控制还是模糊神经网络控制，均增加了系统复杂性与物理实现难度，显然，寻找结构较为简单、控制效果较好且易于实现的控制方案显得十分必要。

5 结 论

本文从数控机床进给系统的机械结构、驱动形式、运动性能检测、力学建模、非线性因素及控制补偿等方面做了综合性的概述，可为今后在进给系统结构设计、性能分析及控制补偿等方面提供基本原理和技术参考。

虽然目前关于进给系统建模及控制补偿等方面的研究取得了一定的成果，但是仍存在一些不足，还应在以下几个方面进一步开展工作：

(1)摩擦一直是进给系统性能提高的主要障碍，主要在系统低速运动和换向时作用明显，针对具体的机床进给系统，建立符合实际情况、理论上比较严格且描述低速特性较好的摩擦力模型，给出适用于工况激励下的参数辨识方法及相应的控制补偿方法是数控加工研究领域的一项关键技术。

(2)在进给系统的研究中，为了降低动力学建模及控制补偿的难度通常都将间隙以定常值处理。随着长期运行、润滑状况及工作环境的变化，进给系统传动机构中的运动副的性能会逐渐退化，导致间隙逐渐增大。因此，在进给系统动力学研究中，应将运动副性能退化模型引入到进给系统的动力学方程中，以使进给系统的相关研究更加为生产实际服务。

(3)进给系统动静态性能的好坏，除了机械结构的影响之外，控制补偿方案起了主要作用。目前控制补偿方法众多，难易程度不等，虽然复合控制提高了进给系统性能，但也增加了系统的复杂性及物理实现难度，寻找结构较为简单、控制效果好及物理上容易实现的控制方案仍是目前进给系统及相关伺服系统性能提高的主要研究热点。

参 考 文 献

[ 1 ] David P, Sylvain L, Claire L, et al. Feed drive modelling for the simulation of tool path tracking in multi-axis High Speed Machining [J]. International Journal of Mechatronics and Manufacturing Systems, 2011，4(3-4): 266-284.

[ 2 ] 刘丽兰, 刘宏昭, 吴子英, 等. 低速下机床进给伺服系统稳定性研究[J]. 振动与冲击, 2010, 29(5): 187-190. LIU Li-lan, LIU Hong-zhao, WU Zi-ying，et al. Stability of feed servo system of a machine tool with low feed velocity [J]. Journal of Vibration and Shock, 2010, 29(5): 187-190.[ 3 ] Lantz M A, Cherubini G, Pantazi A，et al. Servo-pattern design and track-following control for nanometer head positioning on flexible tape media [J]. IEEE Transactions on Control Systems Technology, 2012, 20(2): 369-381.

[ 4 ] 刘定强, 黄玉美, 吴知峰,等. 宏微进给系统位置精度的误差补偿[J]. 机械科学与技术，2011, 30(4): 645-648. LIU Ding-qiang, HUANG Yu-mei, WU Zhi-feng， et al. Position error compensation for a macro-micro feed system [J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(4): 645-648.

[ 5 ] 吴子英, 刘宏昭, 刘丽兰. 考虑摩擦影响的重型车床横向进给伺服系统建模与分析[J]. 机械工程学报, 2012, 48(7): 86-93. WU Zi-ying, LIU Hong-zhao，LIU li-lan. Modeling and analysis of cross feed servo system of heavy duty lathe subjected to friction [J]. Journal of Mechanical Engineering, 2012, 48(7): 86-93.

[ 6 ] 宋江波, 刘宏昭, 原大宁，等. 数控机床传动系统精度可靠性研究[J]. 中国机械工程, 2011, 22(7): 785-789. SONG Jiang-bo, LIU Hong-zhao, YUAN Da-ning, et al. Accuracy reliability research of the transmission system of the numerical control machine [J].China Mechanical Engineering, 2011, 22(7): 785-789.

[ 7 ] 王 胜, 刘宏昭. 基于神经网络的重型数控车床定位精度测量与预测[J].机械科学与技术, 2011, 31(4): 604-608. WANG Sheng，LIU Hong-zhao. Laser measurement and prediction of position accuracy for CNC heavy-duty lathe based on neural network [J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 31(4): 604-608.

[ 8 ] 吴子英, 刘宏昭, 原大宁,等. 某重型车床横向进给系统传动刚度分析与实验研究[J]. 实验力学, 2011, 26(4): 457-463. WU Zi-ying, LIU Hong-zhao, YUAN Da-ning, et al.A stude of analysis and experiment on transmission stiffness of the transverse feed system of a type of heavy duty lathe[J]. Journal of Experimental Mechanics, 2011, 26(4): 457-463.

[ 9 ] 周玉清, 梅雪松, 姜歌东, 等. 基于内置传感器的大型数控机床状态监测技术[J]. 机械工程学报, 2009, 45(4): 125-130. ZHOU Yu-qing, MEI Xue-song, JIANG Ge-dong, et al. Technology on large scale numerical control machine tool condition monitoring based on built-in sensors [J]. Journal of Mechanical Engineering, 2009, 45(4): 125-130.

[10] 周玉清, 梅雪松, 邢建辉, 等. 基于ePS的大型数控机床状态监测及其应用[J]. 工艺与检测, 2009, 2: 104-107. ZHOU Yu-qing, MEI Xue-song, XING Jian-hui ，et al. Application of large scale NC machine tools condition monitoring based on ePS network services [J]. China Mechanical Engineering, 2009, 2: 104-107.

[11] 戴曙. 金属切削机床 [M]. 北京: 机械工业出版社, 2000.

[12] 闫占辉, 王大宇. 数控机床运动部件爬行的临界速度计算[J]. 机床与液压, 2012, 40(11): 61-62. YAN Zhan-hui，WANG Da-yu. Critical speed of moving parts creep to NC machine tools [J]. Machine Tool and Hydraulics, 2012, 40(11): 61-62.

[13] 刘丽兰, 刘宏昭, 吴子英, 等. 考虑摩擦和间隙影响的机床进给伺服系统建模与分析 [J]. 农业机械学报, 2010, 41(11): 212-218. LIU Li-lan, LIU Hong-zhao WU Zi-ying et al. Modeling and analysis of machine tool feed servo systems with friction and backlash [J]. Transactions of the Chinese Society of Agricultural Machinery, 2010, 41(11): 212-218.

[14] Ebrahimi M, Whalley R. Analysis, modeling and simulation of stiffness in machine tool drives [J].Computers & Industrial Engineering, 2000, 38(1): 93-105.

[15] 刘丽兰, 刘宏昭, 吴子英, 等. 机械系统中摩擦模型的研究进展 [J]. 力学进展, 2008, 38(2): 201-213. LIU Li-lan, LIU Hong-zhao, WU Zi-ying et al. An overview of friction models in mechanical system [J]. Advances in Mechanics, 2008, 38(2): 201-213.

[16] 向红标, 谭文斌, 李醒飞, 等.基于 LuGre 模型的自适应摩擦补偿[J]. 机械工程学报, 2012, 48(17): 70-74. XIANG Hong-biao, TAN Wen-bin, LI Xing-fei et al. Adaptive friction compensation based on LuGre model [J]. Journal of Mechanical Engineering, 2012, 48(17): 70-74.

[17] 于伟, 马佳光, 李锦英, 等. 基于LuGre模型实现精密伺服转台摩擦参数辨识及补偿[J].光学精密工程, 2011, 19(11): 2736-2743. YU Wei, MA Jia-guang, LI Jin-ying ，et al. Friction parameter identification and friction compensation for precision servo turning table [J]. Optics and Precision Engineering, 2011, 19(11): 2736-2743.

[18] CHEN Chao-yun，CHENG Ming-yang. Adaptive disturbance compensation and load torque estimation for speed control of a servomechanism [J]. International Journal of Machine Tools & Manufacture, 2012, 59:6-15.

[19] Younkin G W. Modeling machine tool feed servo drives using simulation techniques to predict performance [J]. IEEE Transactions on Industry Applications, 1991, 27(2): 268-274.

[20] Suraneni S, Kar I N, Ramana Murthy O V,et al. Adaptive stick slip friction and backlash compensation using dynamic fuzzy logic system [J].Applied Soft Computing, 2005, 6(1): 26-37.

[21] 陶永华 主编. 新型PID控制及其应用(第2版)[M].北京：机械工业出版社, 2005.

[22] Erkorkmaz K, Altintas Y. High speed CNC system design. Part III: high speed tracking and contouring control of feed drives [J]. International Journal of Machine Tools & Manufacture, 2001, 41(11): 1637-1658.

[23] Lee D H, Ahn J W. Dual speed control scheme of servo drive system for a nonlinear friction compensation [J]. IEEE Transactions on Power Electronics, 2008, 23(2): 959-965.

[24] Han S I, Lee J M. Adaptive dynamic surface control with sliding mode control and RWNN for robust positioning of a linear motion stage [J]. Mechatronics, 2012, 22(2):222 238.

[25] HU Pu-xi, QIAN Wei, LIAO jian. Intelligent control system of CNC mill machieing based on the feed-driven linear motor [J]. Computer and Information Science, 2011, 4(5): 53-59.

Advances in research of feed-servo systems of CNC machine tools

WU Zi-ying, LIU Hong-zhao, WANG Sheng, LIU Li-lan

(School of Machinery and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China)

Aiming to developments of feed-servo systems of CNC machine tools, several structural forms of feed systems were described firstly. The characteristics of each kind of structural form and its applicable cases were analyzed. Then, the methods for performance prediction and detection of feed systems were introduced in detail. The mechanical models of several feed systems and their characteristics were presented. Moreover, the effects of nonlinear factors on the dynamic performance of a feed-servo system were considered. The different control and compensation schemes for friction and backlash were presented in detail. Last, some problems to be further studied were pointed out. This review provided a reference for the research of feed-servo systems in the future.

feed-servo system; transmission structure; performance prediction; mechanical modeling; control and compensation

国家自然科学基金(51205307,51275404);陕西省自然科学基金 (2012JQ7011);陕西省教育厅资助项目(2013JK1001);陕西省重点学科建设专项资金资助项目

2013-03-25 修改稿收到日期：2013-04-26

吴子英 男，博士，副教授，硕士生导师，1975年7月出生

TG580.23

A

10.13465/j.cnki.jvs.2014.08.026