非二元条件约束满足问题求解

袁际军，黄敏镁

（1．广东财经大学 金融学院，广东 广州 510320；2．华南师范大学 管理科学系，广东 广州 510006）

0 引言

约束满足问题（Constraint Satisfaction Problem，CSP）由一组具有有限域的变量以及限制变量间取值组合的约束构成。CSP的解是一组对所有变量的赋值，并使得该赋值满足所有的约束［1－2］。近三十年来，CSP因其强大的知识表示能力及丰富的领域独立求解技术，在越来越多的现实领域中得到广泛应用，如调度问题［3－4］、日程安排问题［5］、配置问题［6－7］等。然而，随着上述问题求解规模的扩大、约束维数的多元化以及解空间变化的动态性，使得CSP直接建模并求解上述问题时，易遇到知识表示及求解上的困难。

为了有效处理变量在约束条件支配下动态参与问题求解的特性，如豪华型汽车需要配置天窗而标准型不必配置天窗（即变量“天窗”是否出现在最终解中，依赖于变量“汽车”的取值是豪华型还是标准型），Mittal和Falkenhainer对CSP进行了扩展，提出了经典的动态约束满足问题（Dynamic Constraint Satisfaction Problems，DCSP）模型［8］。DCSP模型将CSP中的变量划分为初始变量和非初始变量两类，并引入激活性约束建模初始变量与非初始变量以及非初始变量间的条件依赖关系；通过激活性约束动态地控制非初始变量的状态，使之依条件动态参与问题求解并出现在最终解集中。为了区别文献中已有的另一类动态约束满足问题［9］，Sabin将Mittal提出的DCSP模型更名为条件约束满足问题（Conditional Constraint Satisfaction Problems，CCSP）［10－11］，并从二元约束的角度进行了系统的研究。尽管条件约束满足问题及其变体，如Sabin提出的复合约束满足问题（composite constraint satisfaction problems）［12］、Esther提出的混合条件约束满足问题（Mixed and Conditional Constraint Satisfaction Problems，MCCSP）［13］、Mouhoub提出的条件复合约束满足问题（Conditional and Composite Constraint Satisfaction Problems，CCCSP）［5］、Dong Yang［14］以及 Lin Wang［15］提出的改进型动态约束满足问题等，在建模问题的动态性方面拥有更强的知识表示力，然而在求解条件约束满足问题及其变体时，上述文献大都假设只考虑二元约束的情形，并给出直接或间接的求解方法。直接求解方法主要是针对CCSP的特征，在直接求解CCSP时嵌入处理CSP相似的弧一致性技术，以实现对CCSP的直接求解，如在回溯求解期间，嵌入前向检查算法（Forward Checking，FC）或维持弧一致性（Maintaining Arc Consistency，MAC）方法［5］。为进一步提高算法的求解效率，针对条件约束满足问题及其变体在处理激活性约束时，新变量的动态引入对问题一致性状态的影响，Lin Wang等［15］提出了前向检查（Forward Checking，FC）算法与后看检查算法（如回跳算法（Backjumping algorithm，BJ））相结合的混合式算法FC－BJ，以增强传统的回溯算法的求解性能；引入最先失败原则的动态变量排序启发式思想，以改进混合式算法FC－BJ的求解效率，即算法FCBJ－FF；实证表明该算法的求解性能显著优于求解条件约束满足问题的传统回溯算法［8，14］。间接求解方法主要是通过将CCSP转化为标准的CSP［13，16］，通过对CSP的求解来实现对CCSP的间接求解。间接求解方法在处理CCSP时，往往会由于新增约束及变量值域规模的显著扩大，导致问题的求解规模过大，影响求解效率；同时这种转化还易引起建模约束问题时知识表示的不自然。Raphael等［16］基于CCSP转换成CSP时存在的上述不足，提出两种新的建模方法（如对象建模语言Alloy及回答集编程（Answer Set Programming，ASP））用于直接建模CCSP并实现其求解。由于CCSP向Alloy或ASP模型的转化是直接自然的，且Alloy模型可转化为可满足性问题（Satisfiability Problem，SAT）以实现其求解，同时ASP模型也可转化为一种被求解器Cmodels可接受的形式以实现其求解，其中求解器Cmodels的内核也是基于SAT的。然而从算法的角度而言，Raphael只是提出了如何直接建模CCSP的方法，但采用何种算法来实现高效的求解却并未明确给出。

上述研究主要针对二元条件约束满足问题，关注回溯算法与一致性技术的结合。然而，在现实问题中，非二元约束出现得非常频繁。利用非二元约束满足问题领域的已有理论，直接拓展二元条件约束满足问题求解方法，以实现对非二元条件约束满足问题的直接求解，是一种可供尝试的求解途径。在非二元约束满足问题求解方面，目前存在一些较好的算法，如非二元弧一致性（non－binary Forward Checking，nFC）算法［17］、广义弧一致性（Generalized Arc Consistency 2001/3．1，GAC2001/3．1）算法［18］、域过滤一致性算法［19］、关系邻域逆一致性（Relational Neighborhood Inverse Consistency，RNIC）算法［20］等。域过滤一致性算法与关系邻域逆一致性算法RNIC具有强局部一致性特征，在大规模难问题求解时具有一定的优势。其中，算法RNIC主要应用于非二元约束满足问题的对偶图上。在问题规模不大时，实施非二元弧一致算法或广义弧一致算法，会因每次约束检查时代价的降低而带来算法总体效率的提高。然而，在求解非二元条件约束满足问题时，不同于二元CSP中的约束传播方法可直接嵌入到二元CCSP的求解过程中，有些适用于非二元CSP的经典约束传播方法［17］，如nFC1、nFC2和nFC3，并不适用于直接嵌入到带有非二元约束的条件约束满足问题的求解过程中。

本文的关注焦点在于实现对非二元条件约束满足问题的直接求解。

1 非二元条件约束满足问题

非二元条件约束满足问题（Non－binary Conditional Constraint Satisfaction Problem，NCCSP）是一个五元组P＝（V，VI，D，C，A），其中：

（1）集合V 表示一组变量，即V＝｛vi｜i∈｛1，2，…，n｝｝，n表示不同变量的个数。对于任一变量vi∈V，存在三种可能状态，即活动变量（active：vi）、非活动变量（⇁active：vi或inactive：vi）与未定义变量（undefined：vi）。处于活动状态的变量参与问题求解，且在求解过程中需指派域值；处于非活动状态的变量在求解过程中禁止指派域值；处于未定义状态的变量指该变量此时尚未激活，不参与问题求解。

（2）集合VI表示一组非空初始变量，且有VI⊆V。对于任一变量vj∈VI，均处于活动变量状态。

（3）集合D表示一组与变量相对应的值域，即D＝｛D（vi）｜i∈｛1，2，…，n｝｝。其中，D（vi）表示变量vi的值域，本文仅研究离散有限域变量。

（4）集合C表示一组兼容性约束，即C＝｛Cj｜j∈｛1，2，…，｜C｜｝∧S（Cj）⊆V｝，｜C｜表示不同兼容性约束的个数，变量集合S（Cj）称为第j个约束Cj的作用范围。对于∀S（Cj）＝｛vji｜i＝1，2，…，｜S（Cj）｜｝，则 有 Cj⊆D（vj1）×D（vj2）× … ×D（vj｜S（Cj）｜）成立。若∃Ci∈C，使得｜S（Ci）｜＞2，则称该Ci为非二元兼容性约束。如果兼容性约束Cj作用范围中所有变量处于活动变量状态，则该约束称为被激活的兼容性约束；在求解过程中，仅被激活的兼容性约束参与问题求解。

（5）集合A表示一组激活性约束。激活性约束分为包含性约束和排斥性约束：①包含性约束形如：（ ，…， ）incl， ，…， ，

Ccondvivj⇒vk其中条件变量为vivj目

标变量为vk，且有vk∉｛v1，…，vj｝，当条件变量（vi，…，vj）的一组指派与约束条件Ccond（vi，…，vj）一致时，目标变量vk将被触发为活动变量状态；②排斥（ ，…， ）excl，性约束形如：Ccondvivj⇒vk其中目标变量vk∉｛v1，…，vj｝。当条件变量（vi，…，vj）的一组指派与约束条件Ccond（vi，…，vj）一致时，目标变量vk将被触发为非活动变量状态。

定义1 非二元条件约束满足问题的解。NCCSP的解是对所有处于活动变量状态的一个指派Ti，并使得该指派Ti必须满足如下两个要求：①在Ti中的所有变量及其赋值必须满足C∪A；②不存在Ti的子集仍然是NCCSP的一个解。

定义2 约束投影。给定一个约束Ci及约束作用范围S（Ci）的子集Sj，将Sj在约束Ci中对应变量的域值组合加以截留，形成一个作用在变量集合Sj上新的约束关系，这种新的约束关系称为约束Ci在变量集合Sj上的约束投影。令Sj⊆S（Ci），则Ci在Sj上的约束投影形成的新约束记为πSj（Ci）。

定义3 非二元弧一致性。若∃t∈Cj，使得dk∈π｛vi｝（t）成立，则称变量vi的域值dk与约束Cj具有一致性。若∀dr∈D（vi），∃t∈Cj，使得dr∈π｛vi｝（t）成立，则称变量vi与兼容性约束Cj具有一致性。若非二元兼容性约束Cj作用范围S（Cj）中的任一变量vk都与约束Cj具有一致性，则称兼容性Cj是非二元弧一致的。若兼容性约束集合C中的任一约束Ci都是非二元弧一致的，则称兼容性约束集合C是非二元弧一致的。

在NCCSP的求解过程中，动态地构建与NCCSP相关的约束网络。在该约束网络中，所有变量均处于活动变量状态，在求解过程中这些变量均需被指派域值，NCCSP的解由约束网络中的所有变量及其相应赋值组成。

2 非二元条件约束满足问题求解算法

非二元条件约束满足问题是非二元约束满足问题 （Non－binary Constraint Satisfaction Problem，NCSP）与二元条件约束满足问题（Binary Conditional Constraint Satisfaction Problem，BCCSP）的进一步泛化。为了处理NCCSP求解过程中约束维数的非二元性及参与求解变量规模的动态可变性，本文借鉴处理NCSP和BCCSP的求解方法［10，11，17］，提出下述两种不同类型的非二元条件约束满足问题求解算法。

2．1 非二元条件约束满足问题求解的回溯算法

回溯搜索方法是求解约束满足问题的基本方法。根据NCCSP的性质，问题中主要存在激活性约束和兼容性约束两种不同类型的约束。回溯过程中，采用深度优先搜索策略；对每一变量赋值时，相继嵌入激活性约束检查与兼容性约束检查，以求解NCCSP。非二元条件约束满足问题求解的回溯算法流程如图1所示。2．1．1 非二元条件约束满足问题回溯算法

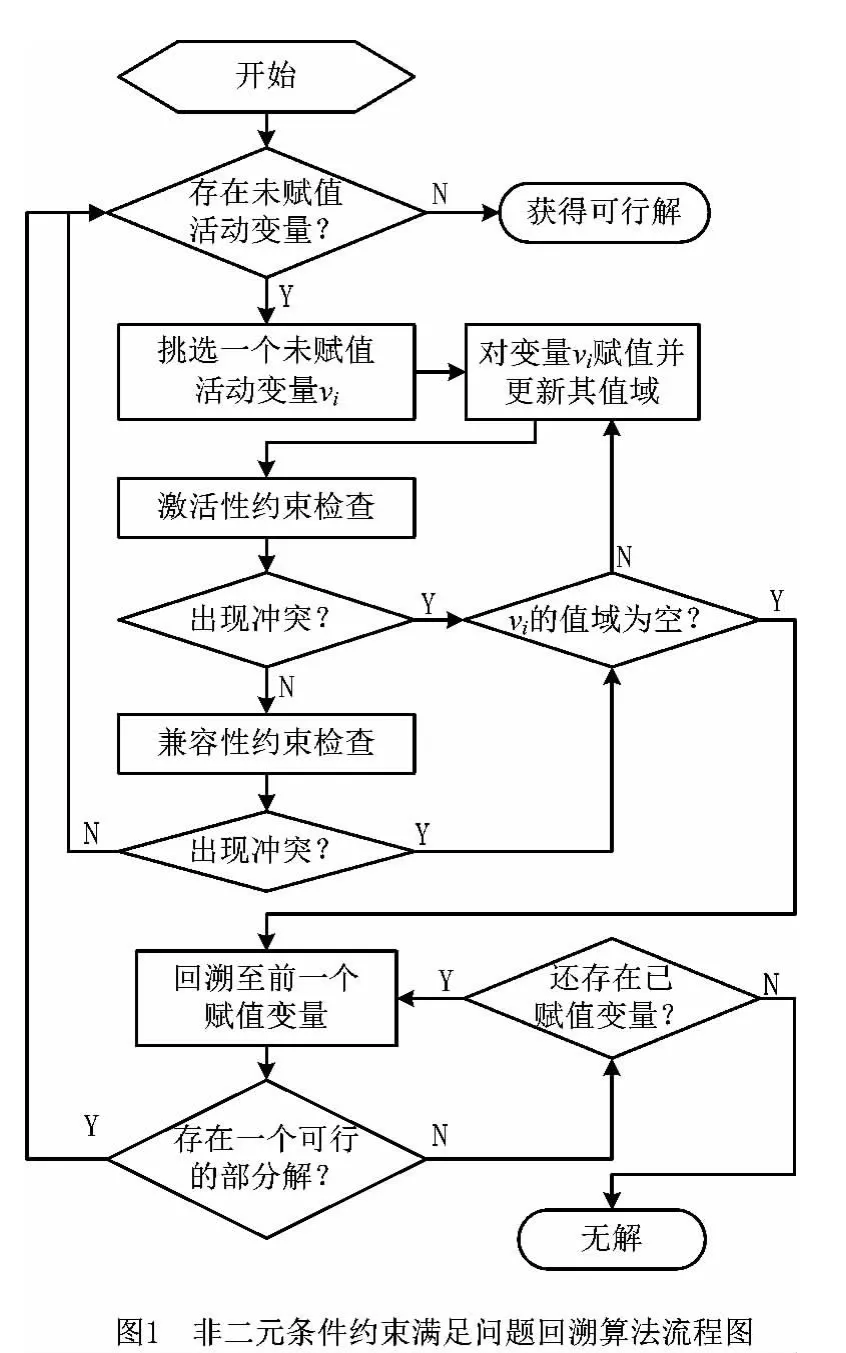
非二元条件约束满足问题回溯算法（Backtrack Search for Non－binary Conditional Constraint Satisfaction Problem，NCCSP－BT）主要采用深度优先方式遍历整个搜索树（算法1）：首先从变量集合Vactive（注：Vactive初始化时所含的变量为NCCSP中的所有初始变量VI）中挑选一个未赋值变量，作为当前变量vrb，并从当前变量值域D｛vrb｝中挑选域值d，实例化该变量vrb；然后针对当前变量的赋值，相继调用子程序激活性约束检查算法activity（）和兼容性约束检查算法compatibility（）进行冲突性检查，若无冲突产生，则从更新后的变量集合Vactive中挑选另一未赋值变量，作为当前变量并进行递归搜索；若出现冲突，则恢复原有信息，再从D｛vrb｝中挑选另一域值，实例化当前变量并重复之前的操作；若D｛vrb｝中的所有域值被遍历后仍有冲突产生，则回溯到上一阶段。程序的终止主要以求解到所需要的解或发现无解为止。

算法1 非二元条件约束满足问题回溯算法（NCCSP－BT）。

boolean NCCSP－BT（i，Vactive，D，C，A，B，values）｛

if（变量i的值大于集合Vactive中元素个数之和）return true//获得一个可行解

vrb←Vactive（i）// 从列表 Vactive中获取当前待赋值变量vrb

for each（d∈D｛vrb｝）｛

将域值d赋予当前变量vrb，并将信息添加到values中

V1←Vactive；B1←B；values1←values；

if（activity（vrb，Vactive，values，A，B）and（compatibility（vrb，Vactive，values，C））｛

i←i＋1；NCCSP－BT（i，Vactive，D，C，A，B，values）；i←i－1｝

Vactive←V1；B←B1；values←values1｝

return false｝//结束 NCCSP－BT（）2．1．2 对激活性约束检查的处理

根据激活性约束的定义，当约束条件中的条件变量未全赋值或条件变量的赋值不满足约束条件时，激活性约束中的目标变量将不会被触发。因此，对激活性约束的检查，仅需要检查约束条件在当前变量赋值下被满足时，其触发的目标变量激活性状态对搜索空间所造成的影响。

在回溯搜索过程中，激活性约束检查算法（算法2）对激活性约束的处理如下：①在激活性约束集合A中，挑选条件变量（包含当前赋值变量vrb）已实例化的所有激活性约束，组成新的约束集合AA。②对激活性约束AA中的每条约束a进行检查：若a的约束条件不被values中的相应条件变量赋值满足时，则当前变量vrb的赋值视为对约束a无影响；若a的约束条件被满足时，当前变量vrb的赋值可能会引发两类冲突而导致该赋值不可行，即包含性约束触发的目标变量已处于活动变量状态，或排斥性约束触发的目标变量已处于非活动变量状态；若无冲突产生，则在结构数组B中记录新触发的活动变量和非活动变量历史信息，并在变量列表Vactive中添加新触发的活动变量。

算法2 激活性约束检查算法。

boolean activity（vrb，Vactive，values，A，B）｛

//Vactive是活动变量列表

令Vactive＝Vassign∪Vunassign

//Vassign是Vactive中已赋值变量列表（包括当前赋值变量vrb）

//Vunassign是Vactive中未赋值变量列表

AA←｛ai｜ai∈A∧cond（ai）⊆Vassign∧vrb∈cond（ai）｝

//A是激活性约束集合，cond（ai）是激活性约束ai的条件变量集

for each（a∈AA）｛

if（a的条件约束被values满足）｛

//values保存迄今已实例化变量的赋值信息

i

f（a是包含性约束）｛i

f（a的目标变量此前已被触发为非活动变量状态）return false else if（a的目标变量此前未被触发）｛

Vactive←Vactive∪｛a的目标变量｝

在结构数组B中添加a的目标变量的历史信息｝｝

else｛//a是排斥性约束

if（a的目标变量此前已被触发为活动变量状态）return false

else if（a的目标变量此前未被触发）｛

在结构数组B中添加a的目标变量的历史信息｝｝｝

return true｝//结束activity（）2．1．3 对兼容性约束检查的处理

在回溯搜索过程中，每次实例化当前变量时，均需进行兼容性约束检查，以检测该变量的实例化是否与相关约束冲突。如果兼容性约束所涉及的受约束变量中不包含当前变量，或除当前变量外还有其他尚未实例化的变量，则对当前变量的实例化不会违反此兼容性约束。因此，约束检查时，只需检查与当前变量相关的兼容性约束。

在兼容性约束检查算法中（算法3），令Vassign是活动变量集合Vactive中的已赋值变量子集，Vunassign是Vactive中的未赋值变量子集，S（Cj）是兼容性约束Cj的约束作用范围，值组values是对迄今已实例化变量的一组指派。算法首先从兼容性约束集合C中，挑选约束作用范围由当前变量vrb和已赋值变量所构成的兼容性约束子集CC（注：CC＝｛Cj｜Cj∈C∧S（Cj）⊆Vassign∧vrb∈S（Cj）｝）；然后对每条兼容性约束CCj∈CC进行冲突性检测，若值组values在约束作用范围S（CCj）上的约束投影π｛S（CCj）｝（values）不满足约束CCj，则表明当前变量vrb赋值与该约束相冲突，使得当前变量赋值不可行。

算法3 兼容性约束检查算法。

boolean compatibility（vrb，Vactive，values，C）｛

令Vactive＝Vassign∪Vunassign

//Vassign是Vactive中已赋值变量列表，Vunassign是Vactive中未赋值变量列表

CC←｛Cj｜Cj∈C∧S（Cj）⊆Vassign∧vrb∈S（Cj）｝

for each（CCj∈CC）｛//vrb是当前赋值变量

if（π｛S（CCj）｝（values）∉CCj）return false｝

return true｝//结束compatibility（）

回溯算法在求解需要较少回溯次数或无回溯次数就能得到解的约束问题时，具有较大的优势。相对其他求解算法而言，在回溯过程中导致搜索失败的相同因素反复出现，是使得回溯算法求解效率低下的主要原因。如果在搜索过程中无视这些因素，将导致过多无效回溯，从而使得算法求解效率低下。因而对回溯算法的改进就在于尽可能早地发现这些影响因素。为此，下面提出一种 “前看”搜索策略，以便提前探测出这些因素并加以处理。

2．2 非二元条件约束满足问题求解的前向检查算法

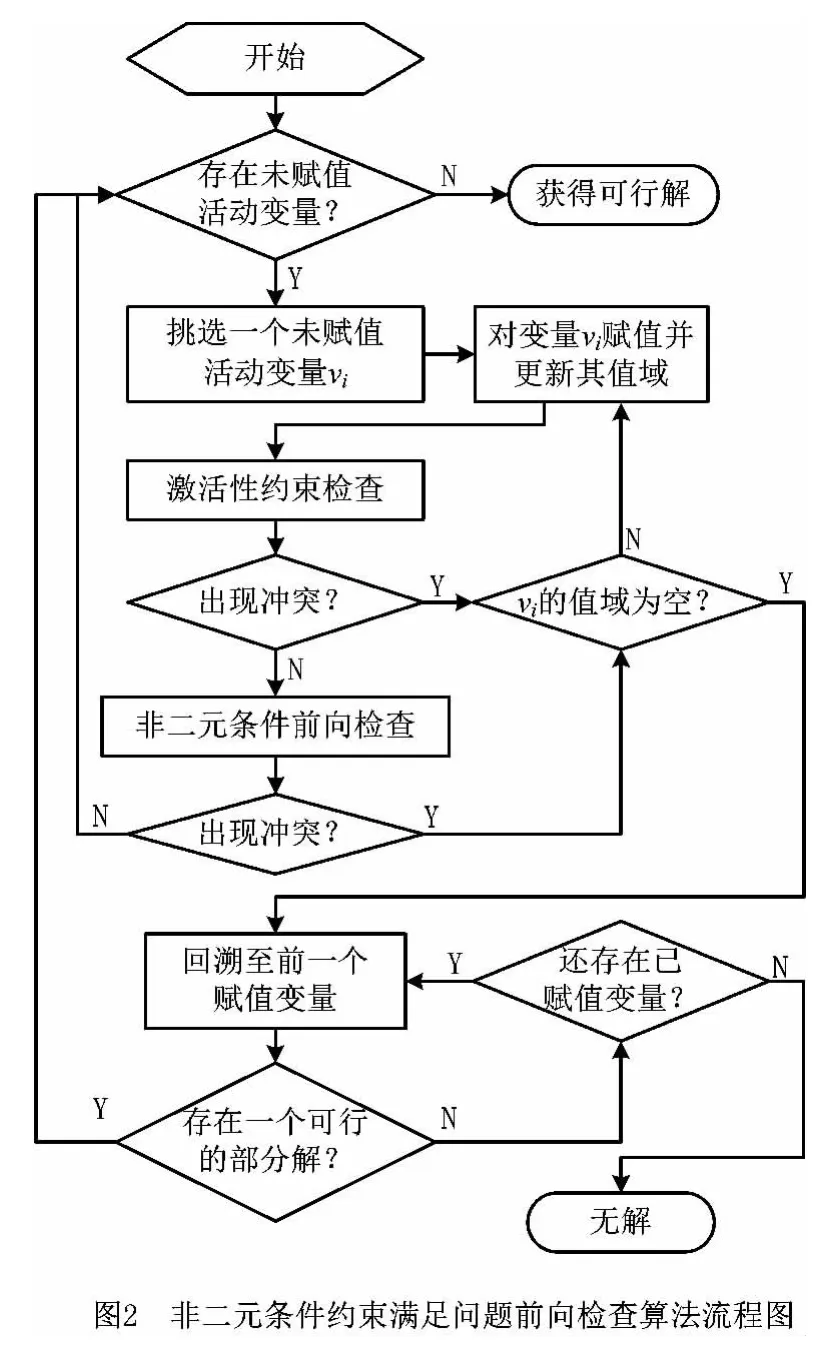
前向约束传播策略［17］是指在求解期间，针对当前变量的赋值，对参与问题求解的变量空间，实施一定程度的局部弧一致性技术，提前剪除所有未赋值变量值域中与已赋值变量（包括当前赋值变量）相冲突的域值，尽早探知无解分支，达到减少搜索空间、提高求解效率的目的。依据非二元条件约束满足问题的特征，结合前向约束传播策略的思想，本文提出求解非二元条件约束满足问题的前向检查算法，如图2所示。

2．2．1 求解NCCSP的前向检查算法

类似于非二元条件约束满足问题回溯算法，前向检查算法同样采用深度优先方式递归遍历整个搜索树。区别在于回溯算法（算法1）采用“回看”的搜索策略，即在每次实例化当前变量后，总是检查当前变量的赋值是否与已赋值变量产生冲突；而非二元条件前向检查算法则采用“前看”的搜索策略，即在每次实例化当前变量后，检查未赋值变量的值域中哪些域值和已赋值变量（包含当前变量）产生冲突，并剔除这些与已赋值变量不一致的未赋值变量域值。根据在前向检查中实施弧一致性程度的不同，前向检查算法又细分为基于NFC4的非二元条件前向检查算法（NCCSP－NFC4）和基于NFC5的非二元条件前向检查算法（NCCSP－NFC5）。NCCSPNFC4算法对搜索过程中每次当前变量赋值后的瞬时状态，通过先后调用子程序activity（）和NFC4（），采用“前看”的搜索策略判断当前的变量赋值是否可行，实施方法见算法4；而NCCSP－NFC5算法则对搜索过程中的每次当前变量赋值后的瞬时状态，通过先后调用子程序activity（）和NFC5（），采用“前看”的搜索策略判断当前的变量赋值是否可行，实施方法见算法5。与回溯算法（算法1）相似，这两类前向检查算法程序主要以求解到所需要的解或发现无解而终止。

算法4 基于NFC4的非二元条件前向检查算法（NCCSP－NFC4算法）。

boolean NCCSP－NFC4（i，Vactive，D，C，A，B，values）｛

if（变量i的值大于集合Vactive中元素个数之和）return true//获得一个可行解

vrb←Vactive（i）//Vactive保存一组被触发的活动变量

for each（d∈D｛vrb｝）｛//vrb是当前赋值变量

将域值d赋予当前变量vrb，并将信息添加到values中；

V1←Vactive；B1←B；values1←values；D1←D；

if（activity（vrb，Vactive，values，A，B）and（NFC4（D，C，Vactive，values））｛

i←i＋1；NCCSP－BT（i，Vactive，D，C，A，B，values）；i←i－1｝

Vactive←V1；B←B1；values←values1；D←D1｝return false

｝//结束 NCCSP－NFC4（）

算法5 基于NFC5的非二元条件前向检查算法（NCCSP－NFC5算法）。

boolean NCCSP－NFC5（i，Vactive，D，C，A，B，values）｛

if（变量i的值大于集合Vactive中元素个数之和）return true//获得一个可行解

vrb←Vactive（i）//Vactive是一组被激活的包含性变量

for each（d∈D｛vrb｝）｛//vrb是当前赋值变量

将域值d赋予当前变量vrb，并将信息添加到values中；

V1←Vactive；B1←B；values1←values；D1←D；

if（activity（vrb，Vactive，values，A，B）and（NFC5（D，C，Vactive，values））｛

i←i＋1；NCCSP－BT（i，Vactive，D，C，A，B，values）；i←i－1｝

Vactive←V1；B←B1；values←values1；D←D1｝

return false

｝//结束 NCCSP－NFC5（）

2．2．2 对激活性约束检查的处理

兼容性约束与激活性约束处理的先后顺序对算法的效率具有较大影响。在面向非二元条件约束满足问题的前向检查算法中，针对当前变量的赋值，如果先进行兼容性约束弧一致操作再进行激活性约束检查操作，则在对激活性约束进行处理后，当有新的目标变量被激活并加入待求解的问题空间时，就需要对这部分被激活的新变量再次实施弧一致性处理，以便在下一阶段挑选出未赋值变量进行赋值时，当前问题已经处于一定程度的弧一致状态。因此，为防止上述繁琐处理过程，本文在求解过程中针对当前变量赋值，均遵循先检查激活性约束、再检查兼容性约束的顺序，以提高算法求解效率。其中，激活性约束检查过程与2．1．2节方法相同。

2．2．3 对非二元条件前向检查中约束传播过程的处理

在非二元条件约束满足问题求解期间，设Vi是变量xi赋值后第i个瞬时状态对应的所有活动变量，Vj是变量xj赋值后第j个瞬时状态对应的所有活动变量，并假定第j个瞬时状态是第i个瞬时状态的后继状态；由于所有非初始变量（V－VI）在求解期间并非总是参与问题求解，可假设Vi≠Vj。令Vi→j＝Vj－Vi，则Vi→j是变量Cactivep，f赋值后所触发的一组新增活动变量。令Cactivej（Cactivej⊆C）是与第j个瞬时状态对应的一组被激活的约束，且有Cactivep，f＝

Cactivec，f∪（Cactivep，f－Cactivec，f）∪Cactivep，p∪Cactivef，f。其中：Cactivec，f 表示包含一个当前赋值变量xj和至少一个未赋值变量的所有被激活的兼容性约束；Cactivep，f表示包含至少一个已赋值变量（当前变量xj也视为已赋值变量）和至少一个未赋值变量的所有已激活的兼容性约束；Cactivep，p表示一组约束范围是已赋值变量构成的被激活的兼容性约束；Cactivef，f表示一组约束范围是未赋值变量构成的被激活的兼容性约束。假设Vi－j中存在变量xj1和xj2，且有xj1∈S（ck）∧ck∈Cactivec，f及xj2∈S（ct）∧ct∈（Cactivep，f－Cactivec，f）；根据文献［17］中的弧一致方法nFC1、nFC2和nFC3，若在约束传播过程中的第j个瞬时状态对约束集合Cactivec，f嵌入弧一致操作，则与约束集合Cactivec，f相关的Vi→j中的变量（如xj1）的域值与已赋值变量具有一致性，但并不能保证与约束集合Cactivec，f无关的Vi→j中变量（如xj2）的域值也与已赋值变量具有一致性。因此，弧一致方法nFC1，nFC2和nFC3不能直接应用于第j个瞬时状态。若在约束传播过程中的第j个瞬时状态以约束集合Cactivep，f为弧一致处理对象，则Vi→j中的变量在弧一致处理后，与已赋值变量不一致的域值将被剔除，从而使变量集合Vj处于一致性状态。因此，文献［17］中的弧一致方法nFC4和nFC5可直接应用于第j个瞬时状态。

根据上述分析，在约束传播过程中提出两种非二元条件弧一致方法，即 NFC4和NFC5（算法NFC4和NFC5的基本思想分别来自于弧一致方法nFC4和nFC5）。其中：①NFC4：仅对集合Cactivep，f中的所有兼容性约束实施一遍非二元弧一致性仅，并剔除未赋值变量值域中与已赋值变量不一致的域值；如果在此过程中发现某个未赋值变量值域变为空集，则表明探测到了一个无解分支，说明当前变量赋值不可行，实施方法见算法6。②NFC5：对集合Cactivep，f中的所有兼容性约束实施非二元弧一致，使所有兼容性约束在实施非二元弧一致性处理后均达到弧一致状态；如果在此过程中发现某个未赋值变量值域变为空集，则表明探测到了一个无解分支，说明当前变量赋值不可行，实施方法见算法7。

算法6 NFC4算法。

boolean NFC4（D，C，Vactive，values）｛

令Vactive＝Vp∪Vf

//Vp是Vactive中已赋值变量（包括当前赋值变量）集合，Vf是Vactive中未赋值变量集合

Cactive← ｛Cj｜Cj∈C∧S（Cj）⊆Vactive

｝p，f0（S（C）－V）S（C）∧ ＜｜jp｜＜｜j｜

for each（c∈Capc，tfive）｛

for each（v∈（S（c）∩Vf））｛

//v是兼容性约束c作用范围中的未赋值变量

for each（val∈D｛v｝）｛

if（not（变量v的域值val与约束c具有一致性））｛D｛v｝←D｛v｝－｛val｝

If（D｛v｝等于空集）return false｝｝｝｝

return true｝//结束NFC4（）

算法7 NFC5算法。

boolean NFC5（D，C，Vactive，values）｛令 Vactive＝Vp∪Vf；

Cactive← ｛Cj｜Cj∈C∧S（Cj）⊆Vactive

｝；p，f0（S（C）－V）S（C）∧ ＜｜jp｜＜｜j｜

CC←Capc，tfive

；while（CC≠∅）｛

CC←CC－｛Cj｝；

for each（v∈（S（Cj）∩Vf））｛

//v是兼容性约束c作用范围中的未赋值变量

revise＝false；

for each（val∈D｛v｝）｛

if（not（变量v的域值val与约束c具有一致性））｛

D｛v｝←D｛v｝－｛val｝；revise＝true｝｝if（revise＝＝true）｛

if（D｛v｝等于空集）return false；CC←CC∪｛Ci｜Ci∈Capc，tfive∧v∈S（Ci）∧i≠j｝｝｝｝return true｝//结束NFC5（）

2．3 算例

变量集V＝｛v1，v2，v3，v4，v5，v6｝，其中初始变量集VI＝｛v1，v2，v3，v4｝。每个变量的值域D都是｛e，f，g｝，兼容性约束｛C1，C2，C3｝与激活性约束｛A1，A2，A3｝分别如表1所示。

为阐述3种算法间的差异，表2和表3分别展示了一个简单算例的处理过程。它由4个初始变量｛v1，v2，v3，v4｝和2个非初始变量｛v5，v6｝组成，每个变量分享相同的值域｛e，f，g｝，服从3个兼容性约束｛C1，C2，C3｝和3个激活性约束｛A1，A2，A3｝。其中：A1和A2是包含性约束，A3是排斥性约束。

表1兼容性约束与激活性约束表示

表2 变量v1 和v2相继实例化时不同算法对约束处理的差异

表3 变量v1和v2相继实例化时不同算法所致的域值过滤

在变量v1赋值e（即（v1，e））之后，没有约束含有两个已实例化的变量（包括当前变量v1）。因此，算法NCCSP－NBT对非初始变量｛v5，v6｝的当前状态无影响，也不过滤任何变量的域值。算法NCCSP－NFC4对激活性约束｛A1，A2，A3｝和兼容性约束C3无影响；在先后对约束C1和C2应用非二元弧一致方法后，从D｛v2｝、D｛v3｝和D｛v4｝中删除了域值g。值得注意的是，如果以不同的顺序处理这些约束，过滤效果将会有所不同。算法NCCSP－NFC5对激活性约束｛A1，A2，A3｝和兼容性约束C3无影响；在对约束集｛C1，C2｝应用非二元弧一致方法后，从D｛v2｝中删除了域值f和g，从D｛v3｝和D｛v4｝中删除了域值g。

在变量v2赋值e（即（v2，e））之后，激活性约束A1和A3的约束条件分别得到满足。因此，算法NCCSP－NBT对A1和A3处理之后，导致变量v5的状态由未定义变为活动状态，变量v6的状态由未定义变为非活动状态；由于约束C1、C2和C3所包含的变量未完全实例化，所有算法NCCSP－NBT对所有兼容性约束无影响，也不过滤任何变量的域值。算法NCCSP－NFC4先对激活性约束A1和A3进行检查，然后对兼容性约束C1、C2和C3实施一遍非二元弧一致；导致变量v5的状态由未定义变为活动状态，变量v6的状态由未定义变为非活动状态；从D｛v3｝中删除了域值f，从D｛v5｝中删除了域值f和g。算法NCCSP－NFC5先对激活性约束A1和A3进行检查，再对约束｛C1，C2，C3｝实施弧一致方法，直至所有兼容性约束达到弧一致状态；导致变量v5的状态由未定义变为活动状态，变量v6的状态由未定义变为非活动状态；从D｛v3｝中删除了域值f，从D｛v4｝中删除了域值f，从D｛v5｝中删除了域值f和g。

3 算法复杂性分析

为了更好地衡量非二元条件约束满足问题回溯算法与两类前向检查算法的性能，本章给出最坏情况下的时间复杂度分析，然后证明其正确性。

定理1 非二元条件约束满足问题回溯算法（NCCSP－BT算法）在每个节点最坏的情况下，所消耗的时间复杂度是O（tam｜A｜＋m｜C｜）。

证明 在实例化变量xi时，令AAi为约束条件包含变量xi的一组激活性约束，CCi为约束范围包含变量xi的一组兼容性约束。

（1）令AAi中激活性约束aij包含的目标变量个数为tij，则D｛xi｝中的每个域值d实例化xi时，若满足激活性约束aij的约束条件，则需进一步检查每个目标变量是否与已知状态产生冲突。因此，实例化变量xi时，对激活性约束aij检查的时间复杂度为O（tij｜D｛xi｝｜）。如果变量的域值规模最大为m，激活性约束所触发的目标变量数目最大为ta，激活性约束AAi最坏情况下的最大规模为｜A｜，则实例化变量xi时，最坏情况下对所有相关激活性约束检查的时间复杂度为O（tam｜A｜）。

（2）实例化变量xi时，对每一条兼容性约束的一致性检查，最坏情况下的时间复杂度为O（m）；若CCi最坏情况下的规模最大为｜C｜，则实例化变量xi时，最坏情况下对所有相关兼容性约束检查的时间复杂度为O（m｜C｜）。由于NCCSP＿BT算法的性能主要由激活性约束检查与兼容性约束检查决定，在最坏情况下，对每个节点所消耗的时间复杂度是O（tam｜A｜＋m｜C｜）。

定理2 非二元条件前向检查算法NCCSPNFC4和NCCSP－NFC5在每个节点最坏的情况下，具有相同的时间复杂度O（tam｜A｜＋（rc－1）mrc－1｜Cactivep，f｜）。

证明 在实例化变量xi时，令Cactivep，f表示包含至少一个已赋值变量（当前变量xi也视为已赋值变量）和至少一个未赋值变量的所有已激活的兼容性约束。设Cactivep，f中的一条兼容性约束ci的约束维数为ri，则算法 NCCSP－NFC4对ci检查时，ci中至多包含ri－1个未赋值变量。因此，在对ci实施弧一致性时，最坏情况下算法NCCSP－NFC4的时间复杂度为O（（ri－1）mri－1）。如果Cactivep，f中兼容性约束的最大维数为rc，则在实例化变量xi时，最坏情况下算法NCCSP－NFC4对兼容性约束检查的时间复杂度为O（（rc－1）mrc－1｜Cactivep，f｜）。由定理1的分析可知，在实例化变量xi时，对激活性约束检查的时间复杂度为O（tam｜A｜）。因此，算法NCCSP－NFC4在每个节点最坏情况下所消耗的时间复杂度为O（tam｜A｜＋（rc－1）mrc－1｜Cactivep，f｜）。

在搜索过程中，对于给定的节点，算法NCCSPNFC4和NCCSP－NFC5的主要区别在于对兼容性约束集合Cactivep，f实施弧一致性程度的不同。算法NCCSP－NFC4仅对Cactivep，f中的约束实施一次弧一致，而算法NCCSP－NFC5对Cactivep，f实施弧一致直到所有约束都处于弧一致性状态。文献［17，21］表明，在嵌入某种优化算法如GAC2001时，算法NCCSPNFC4和 NCCSP－NFC5对Cactivep，f实施弧一致，可具有相同的最坏时间复杂度。

4 应用实例分析与基于随机问题的仿真实验

4．1 评价指标

对非二元条件约束满足问题求解算法性能的衡量，本文主要采用如下评价指标：①求解时间，指在求得问题的一个可行解或无解时所耗费的运行时间；②回溯次数，指在求解过程中遇到一个无解状态而不得不回溯到前一求解状态的次数；③兼容性约束检查次数，指在判断当前变量赋值是否为一个有效赋值而对兼容性约束进行检查的有效次数；④条件约束检查次数，指对当前变量赋值后，判断目标变量是否被触发而对激活性约束进行检查的次数。

4．2 NCCSP的应用实例

4．2．1 应用实例及建模

在产品配置领域，功能与实现该功能的组件间是典型的多对多关系。根据“关键组件理论”［8，22］，每个功能都存在实现其功能的关键组件，该关键组件要么完整地实现该功能，要么和其他非关键组件共同作用实现该功能。一旦实现某一功能的关键组件被确定，则与之相关的非关键组件也需要随之依条件动态确定。另外，关键组件存在不同的组件类型，不同的组件类型所实现的功能也存在差异，从而导致实现某一特定功能所需配套的非关键组件集也不相同。在建模为非二元条件约束满足问题模型时，产品功能可分别建模为变量，实现该功能的关键组件类型建模为该变量的域值，为配合关键组件类型实现某一特定功能的非关键组件，采用激活性约束进行建模，产品功能间的约束可建模为兼容性约束。

根据以上理论，以一个简化的某汽车产品配置问题为例［8，10］，根据该制造商的实际制造能力和客户的要求，建立该配置问题的NCCSP模型。在该配置问题中，有8个可配置对象，其中3个是必选可配置对象，5个是非必选可配置对象。这些可配置对象间存在：①4个兼容性约束，包括2个二元约束和2个三元约束；②11个激活性约束，包括8个包含性约束和3个排斥性约束。这些可配置对象和配置约束均被抽象为非二元条件约束满足问题中相应的变量和变量间的约束，并建立如图3所示的面向该产品配置问题的NCCSP模型。4．2．2 实例模型求解

对4．2．1节的NCCSP模型，分别采用本文提出的三种算法进行求解，实验环境为Windows XP，Intel（R）Core（TM）2Duo CPU T7100 ＠1．80 GHz 1．79GHz，0．99GB 的 内 存，编 程 语 言 为MATLAB 7．1。求解到第一个可行解时的实验结果如表4所示。

由表4可知，在获得第一个可行解时，算法NCCSP－BT和 NCCSP－NFC4具有相似的时间性能，算法NCCSP－NFC5具有最坏的时间性能。进一步分析发现，相对于条件约束检查次数，兼容性约束检查次数对算法的性能影响相对较大。

表4 汽车产品配置问题的NCCSP模型的求解结果

需要指出的是，该实例分析的目的并不在于比较各算法的相对求解性能，而在于通过该实例引出NCCSP的一个应用场景。在现实问题中，变量间经常存在复杂的约束，这些约束很多是以非二元约束的形式存在。在涉及必选变量和可选变量的场合，由于在问题最终解中可选变量允许以非赋值的形式存在，导致在求解期间并非所有变量都参与求解。因此，在建模这类问题时，可利用激活性约束依条件动态引入或剔除参与求解的可选变量，从而增加模型的表示力和求解效率。本例的配置问题便是一种典型的NCCSP的应用。

4．3 基于随机问题的仿真实验

4．3．1 仿真实验数据的产生

在4．2节，由于实例较简单，并不能充分揭示各算法性能的相对差异。为进一步比较本文所提算法的求解性能，需要使用随机发生器生成的NCCSP实例。因此，借鉴文献［10］开发的二元条件约束满足问题随机生成器的方法，采用 MATLAB 7．1开发了一个NCCSP随机生成器。

该随机生成器在生成测试实例时，采用如下参数作为输入变量：①n为全体变量个数；②m为变量的最大域值规模，在生成随机问题时将所有变量的域值规模都固定为m；③rc为兼容性约束的最大维数，在生成随机问题时将兼容性约束的维数都固定为rc；④ra为激活性约束中的约束条件的最大维数，在生成随机问题时将激活性约束中约束条件维数都固定为ra；⑤pnoni为非初始变量生成的概率，随机问题中非初始变量规模为npnoni，初始变量规模为n（1－pnoni）；⑥sc为兼容性约束被满足的概率，随机问题中每个兼容性约束所包含的合法元组规模为scmrc；⑦dc为兼容性约束密度，随机问题中所包含的兼容性约束的规模为dcCrnc；⑧sa为激活性约束被满足概率，具有相同条件变量的激活性约束中，其约束条件的合法元组规模为samra；⑨da为激活性约束密度，具有不同条件变量的激活性约束规模为daCrna；具有相同条件变量的激活性约束，其差异主要取决于条件变量取值的不同，激活性约束的总规模为samradaCrna；⑩pincl为每条产生的激活性约束是包含性约束的概率，排斥性约束生成的概率则为（1－pincl）；○11ta为激活性约束所触发的最大目标变量数目。

4．3．2 仿真实验条件设定与实验结果

在面向非二元条件约束满足问题的回溯算法和前向检查算法中，兼容性约束与激活性约束处理的先后顺序对算法性能存在一定的影响。为了评估本文所提算法性能的差异及不同类型约束处理顺序对算法造成的影响，本文仿真实验由两部分构成：①实验一，衡量在不同类型NCCSP实例下本文所提三种算法的性能差异；②实验二，衡量在调整不同类型约束处理顺序后，原算法及其相应变体的性能差异。4．3．2．1 实验一

在生成的随机非二元条件约束满足问题中，本文设定公共参数为：rc＝3，ra＝2，da＝0．5，pincl＝0．5，ta＝1；其他参数取值可变。在相同的一组实验参数下，每次产生100个随机测试实例，实验结果分别取各评价指标的算术平均值。实验环境为Windows XP，Intel（R）Core（TM）2Duo CPU T7100＠1．80GHz 1．79GHz，0．99GB的内存，编程语言为MATLAB 7．1。

（1）不同约束密度下各类约束被满足概率变化时的算法性能

分别研究在不同兼容性约束密度下，兼容性约束与激活性约束被满足概率变化时，本文三种算法的求解性能。设计两组实验：①n＝15，m＝7，pnoni＝0．5，sa＝0．5，dc＝［0．3，0．5，0．7］，sc＝ ［0．1，0．2，0．3，0．4，0．5，0．6，0．7，0．8，0．9］；实验结果如图4所示；②n＝15，m＝7，pnoni＝0．5，sc＝0．5，dc＝［0．3，0．5，0．7］，sa＝ ［0．1，0．2，0．3，0．4，0．5，0．6，0．7，0．8，0．9］。实验结果如图5所示。

由图4可知，相同兼容性约束密度dc下，三种算法在兼容性约束被满足的概率sc由小变大时，运算时间均经历了由快到慢、进而由慢到快的过程；同时可见，当sc在区间［0．4，0．8］内变化时，运算时间发生了显著变化，问题开始变得难以求解；此时，算法NCCSP－BT具有最坏的求解性能，其次是NCCSP－NFC5，再次是 NCCSP－NFC4。另外，不同兼容性约束密度dc下，当兼容性约束被满足的概率sc在区间［0．4，0．7］变化时，所有 NCCSP问题均开始变得难以求解。上述现象表明：①在兼容性约束被满足概率sc很小时，所产生的随机测试实例以无解问题为主，三种算法均能快速探测到一个无解状态；②在兼容性约束被满足概率sc很大时，所产生的随机测试实例可行解非常多，此时，三种算法均能很容易地将一个部分实例化解扩展为一个有效解；③兼容性约束被满足概率sc在区间［0．4，0．8］内变化时，所产生的随机测试实例变得难以求解，原因在于部分实例化解向有效解扩展的过程中，引起搜索失败的因素反复出现，从而导致求解困难。算法NCCSP－NFC4和NCCSP－NFC5在搜索过程中分别嵌入不同程度的弧一致技术，能够有效地剪去不必要的搜索分支，减少求解过程中的回溯次数，因而在难问题上具有比算法NCCSP－BT更优的时间性能。

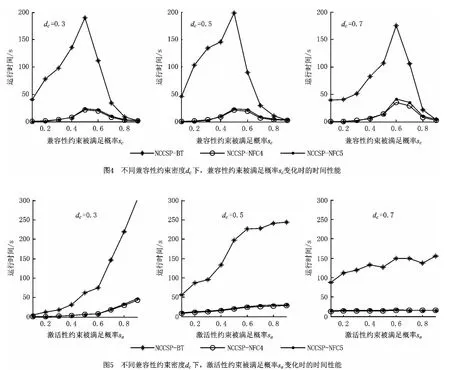
从图5可知，相同兼容性约束密度dc下，三种算法的运算时间均随着激活性约束被满足概率sa的变大而增加；其中，算法NCCSP－BT具有最坏的求解性能，其次是NCCSP－NFC5，再次是 NCCSPNFC4。另外，随着兼容性约束密度dc的增加，三种算法在求解相同问题时，运算时间增加所引起的时间性能曲线均趋向于平缓。上述现象表明：①在激活性约束被满足的概率sa较小时，激活性约束的目标变量被触发的可能性较低；因而在问题求解过程中变量规模的变化不显著，此时问题易于求解；随着激活性约束被满足概率sa的增大，激活性约束的目标变量被触发的可能性也随之增加，从而导致问题求解过程中变量规模的变化愈来愈显著，问题开始变得难以求解。②兼容性约束密度dc的不断增加，使得问题中兼容性约束的规模不断变大，从而增加了一个部分实例化解扩展为有效解的难度。由于在求解过程中，算法 NCCSP－NFC4和 NCCSP－NFC5嵌入了不同程度的弧一致技术，预先剪去后续不必要的搜索分支，提高了求解性能。

（2）不同程度动态性特征时算法性能

由图4和图5可知，算法 NCCSP－NFC4和NCCSP－NFC5在求解NCCSP问题时，其时间性能均显著地优于算法 NCCSP－BT；而算法 NCCSPNFC4和NCCSP－NFC5两者间的求解性能差异却并不显著。下面进一步比较具有不同程度动态性特征 的 NCCSP 问 题 下，算 法 NCCSP－NFC4 和NCCSP－NFC5的相对求解性能。设定实验条件如下：n＝15，m＝7，sa＝0．5，dc＝0．5，sc＝0．5，pnoni＝［0．1，0．2，0．3，0．4，0．5，0．6，0．7，0．8，0．9］，实验结果如图6所示。

非初始变量生成概率pnoni决定了NCCSP中全体变量被划分为初始变量集合与非初始变量集合各自的相对规模。pnoni值越大，变量被挑选作为非初始变量的可能性越大，从而使得解空间的规模也随之增大；在求解过程中，NCCSP问题将展示更强的动态性特征，即更多的非初始变量将频繁动态地被挑选参与到求解过程中。由图6可知，当pnoni值超过0．6的临界点时，算法NCCSP－NFC4和NCCSPNFC5在时间性能上无显著差异；当pnoni＜0．6时，算法NCCSP－NFC4具有比NCCSP－NFC5更佳的时间性能。同时可知，当pnoni值在区间［0．4，0．6］变化时，两种算法的求解性能均发生了显著变化，问题开始变得难以求解。上述现象表明：①pnoni＜0．6时，算法NCCSP－NFC5在求解过程中嵌入更深程度的前看策略所带来的回溯次数减少的收益，并不能弥补求解过程中因实施更深程度前看策略所需要花费的更多兼容性约束检查次数而付出的代价，从而使得算法NCCSP－NFC4在pnoni值小于0．6时具有相对更佳的求解性能；②当pnoni＞0．6时，相对算法NCCSP－NFC4而言，算法NCCSP－NFC5在求解时实施更深程度的前看策略所带来的收益，与其实施该技术所需付出的代价大致相当，因而在此情况下两种算法的相对性能差异并不显著；③从图6还可知，两种算法的时间性能曲线与兼容性约束检查次数曲线的形状非常相似，说明算法的时间性能基本上决定于求解过程中其所执行的兼容性约束检查次数；同时亦说明相对于条件约束检查，执行一次兼容性约束检查需花费更多的时间代价。

（3）问题规模变化时算法性能

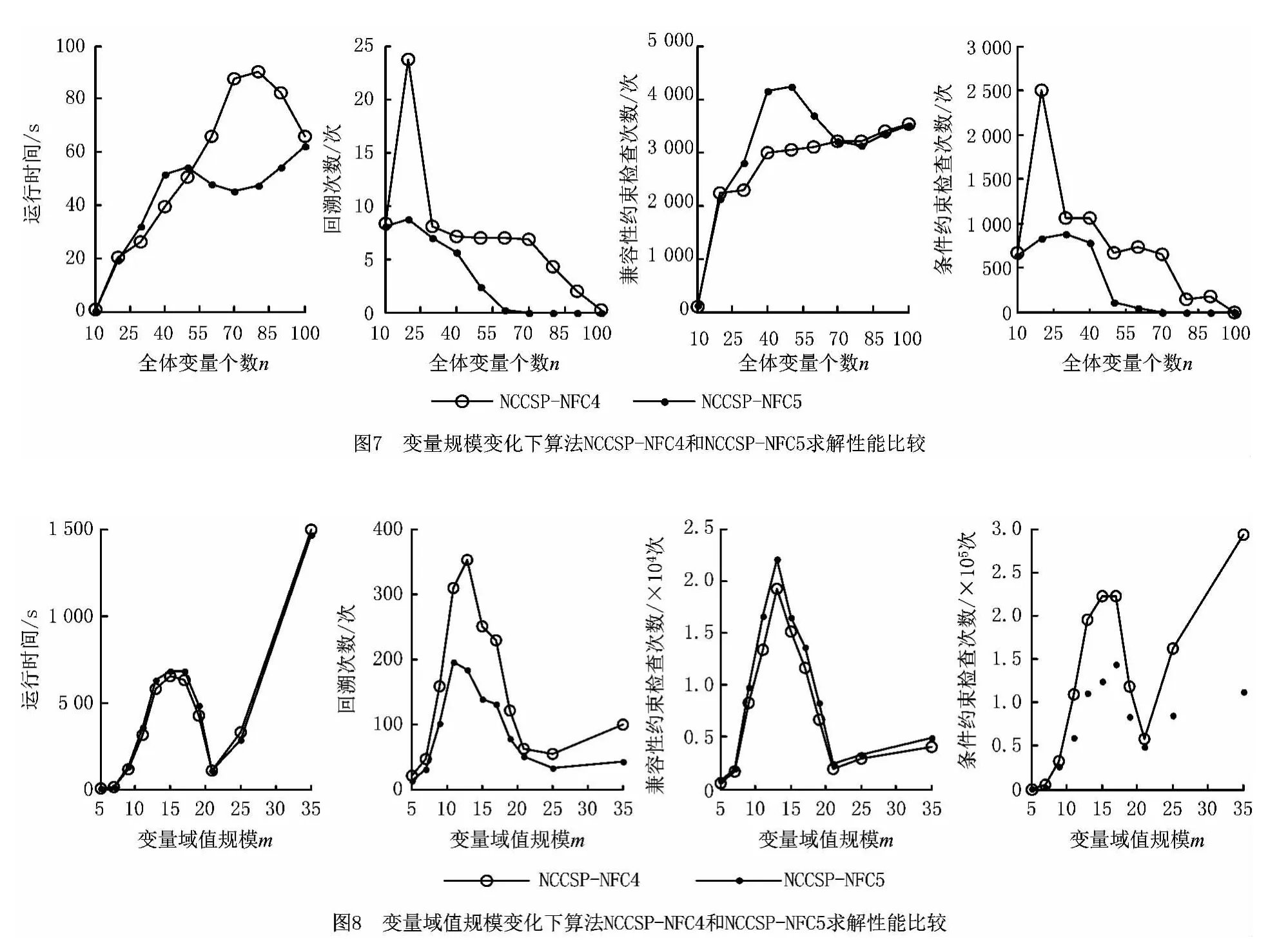
在前述实验中，本文固定变量规模为15和变量域值规模为7，该问题实际上代表了一类规模不大的NCCSP。由于NCCSP解空间规模主要取决于全体变量及其域值的规模，本节分别研究在不同变量规模和变量域值规模下，算法NCCSP－NFC4和NCCSP－NFC5的相对性能。设计两组实验：①n＝［10，20，30，40，50，60，70，80，90，100］，m＝7，pnoni＝0．5，sa＝0．5，dc＝0．5，sc＝0．5；实验结果如图7所示；②n＝15，m＝ ［5，7，9，11，13，15，17，19，21，25，35］，pnoni＝0．5，sa＝0．5，dc＝0．5，sc＝0．5。实验结果如图8所示。

由图7可知，在变量规模小于临界点50时，算法NCCSP－NFC4的时间性能更优；而当变量规模超过临界点50时，算法NCCSP－NFC5的时间性能更优。在回溯次数上，算法NCCSP－NFC5由于在求解过程中实施更深程度的前看策略，删除了更多不必要的搜索分支，具有相对于算法NCCSP－NFC4更优的回溯性能。从图8可知，在变量域值规模小于临界点21时，算法NCCSP－NFC4的时间性能更优；而当变量域值规模大于临界点21时，算法NCCSP－NFC5的时间性能更优。在回溯次数上，算法NCCSP－NFC5始终具有比算法 NCCSP－NFC4更优的回溯性能。上述现象表明：①回溯性能的改善并不一定带来算法时间性能的改善，只有当实施更深程度前看策略所带来的收益大于所付出的代价时，回溯性能的改善才带来算法时间性能的改善；②算法NCCSP－NFC4和NCCSP－NFC5具有不同的适用区间，总体而言，算法NCCSP－NFC4适用于求解中小规模的NCCSP问题；而算法NCCSP－NFC5则适用于求解大规模的NCCSP。4．3．2．2 实验二

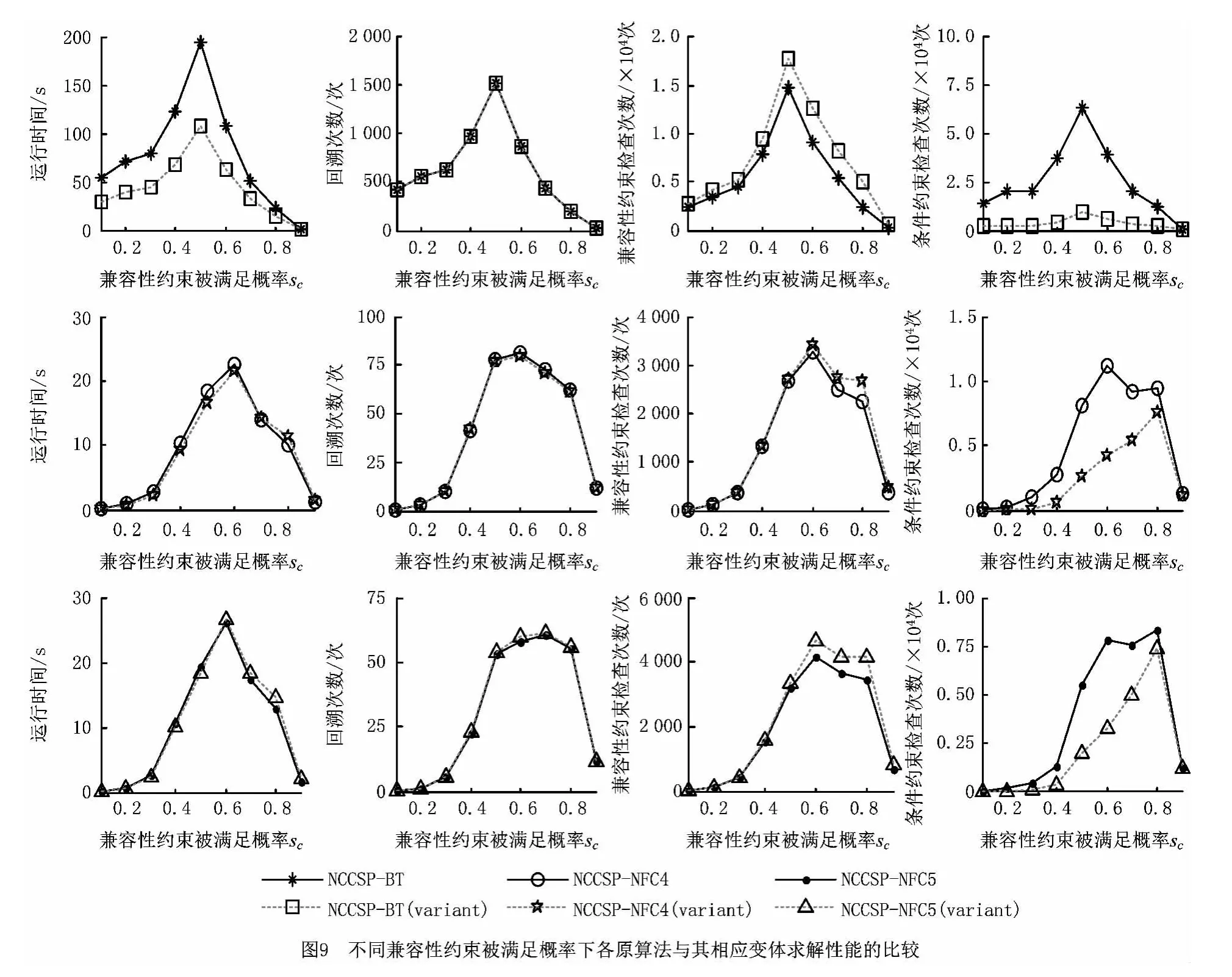
在本文所提的原算法中，对约束的处理均遵循先激活性约束再兼容性约束的顺序。若调整不同类型的约束处理顺序，为保证调整后算法的正确性，需对原算法进行一定的修改。回溯算法NCCSP－BT中，若先处理兼容性约束、再处理激活性约束，则激活性约束所激活的目标变量会改变当前状态问题的拓扑结构；但由于回溯算法对兼容性约束的检查采用“后看”策略，约束处理顺序的改变并不会影响算法的正确性。本文将先处理兼容性约束，再处理激活性约束的回溯算法视为算法NCCSP－BT的变体，称为NCCSP－BT（variant）。在面向非二元条件约束满足问题的前向检查算法中，若进行兼容性约束非二元弧一致操作使得问题处于弧一致状态，则再进行激活性约束处理会导致新激活的活动变量集破坏之前问题的弧一致状态，此时需要在对新产生的活动变量集和已赋值变量集之间进行非二元弧一致操作，以维护所有的未赋值变量与已赋值变量间的弧一致性，从而确保后续阶段赋值操作的正确性。在前向检查算法中先对兼容性约束实施NFC4操作，再在激活性约束处理中对新激活的活动变量集与已赋值变量集嵌入NFC4操作，这种算法视为NCCSP－NFC4的变体，称为 NCCSP－NFC4（variant）。另外，在前向检查算法中，先对兼容性约束实施NFC5操作，再在激活性约束处理中对新激活的活动变量集与已赋值变量集嵌入NFC5操作，这种算法视为 NCCSP－NFC5的变体，称为 NCCSPNFC5（variant）。为衡量各原算法与其相应变体的算法性能差异，限于篇幅，本文仅给出下述设计参数取值时的仿真结果（如图9）：n＝15，m＝7，pnoni＝0．5，sa＝0．5，dc＝ 0．5，sc＝ ［0．1，0．2，0．3，0．4，0．5，0．6，0．7，0．8，0．9］。

从图9可知，不同类型约束处理的先后顺序对算法性能的确具有一定影响。相对原算法而言，先处理兼容性约束、再处理激活性约束，对原算法的求解性能有一定的改善作用。其中，回溯算法NCCSP－BT（variant）相对原算法 NCCSP－BT而言，在约束检查上，以兼容性约束检查次数增加的轻微代价，换取了条件约束检查次数的显著降低，从而节省了搜索成本，使得回溯算法NCCSP－BT（variant）的时间性能比原算法NCCSP－BT得到了明显的改善。在前向检查算法上，原算法变体（NCCSPNFC4（variant）和 NCCSP－NFC5（variant））相对原算法（NCCSP－NFC4、NCCSP－NFC5）而言，其条件约束的检查次数显著减少，也使得其时间性能均获得了轻微改善。

5 结束语

本文对经典二元条件约束满足问题进行了拓展，给出了非二元条件约束满足问题模型。借鉴求解非二元约束满足问题的传统回溯算法及几类前向检查算法思想，结合非二元条件的约束满足问题特征，提出了适于求解非二元条件约束满足问题的回溯算法及前向检查算法。其中，前向检查算法根据其在求解过程中实施局部一致性方法程度的不同，又细分为NCCSP－NFC4和NCCSP－NFC5两种算法。通过一个算例演示了三种算法的求解思想，给出了三种算法最坏情况下的时间复杂性，指出在嵌入某种优化算法（如GAC2001）时，算法NCCSP－NFC4和NCCSP－NFC5最坏情况下具有相同的时间复杂性。通过一个简化的汽车产品配置问题实例阐述了NCCSP的应用场景，开发了随机生成器并生成了NCCSP测试实例，对三种算法的求解性能进行了仿真实验。实验结果发现，在求解难问题时，回溯算法 （NCCSP－BT）性能显著劣于 NCCSPNFC4算法和NCCSP－NFC5算法，而算法NCCSPNFC4和NCCSP－NFC5间的求解性能差异并不显著。进一步分析发现，在中小规模问题中，问题本身所呈现的动态性特征越低，越适用于采用算法NCCSP－NFC4求解，而在高动态性特征问题中，算法NCCSP－NFC4和NCCSP－NFC5之间的求解性能差异并不显著。在大规模问题中，算法NCCSPNFC5在求解性能上优于算法NCCSP－NFC4。总体而言，算法NCCSP－NFC4和NCCSP－NFC5在求解非二元条件约束满足问题时，不存在一个普适区间，某种算法的性能始终优于另一种算法；但在不同的某特定区间，算法 NCCSP－NFC4和 NCCSPNFC5在求解性能上表现出了较显著的差异。需要指出的是，在本文所提的原算法中，若改变不同类型约束的处理顺序，即先处理兼容性约束、再处理激活性约束，则会对原算法的性能带来一定的改善作用。另外，本文所提的三种算法均为直接求解算法，未来将提出适用于NCCSP的间接求解算法和启发式算法，并比较它们与直接求解算法之间的性能差异。

［1］ WANG Ziwen，LI Zhanshan，AI Yang，et al．Algorithm for solving constraint satisfaction problems based on dynamic value ordering heuristic［J］．Computer Integrated Manufacturing Systems，2011，17（4）：832－837（in Chinese）．［王孜文，李占山，艾 阳，等．基于动态值启发式的约束满足求解算法［J］．计算机集成制造系统，2011，17（4）：832－837．］

［2］ LI Zhanshan，LI Hongbo，ZHANG Yonggang，et al．An approach of solving constraint satisfaction problem based on cycle－cut［J］．Chinese Journal of Computers，2011，34（8）：1528－1535（in Chinese）．［李占山，李宏博，张永刚，等．一种基于环切割的约束满足问题求解算法［J］．计算机学报，2011，34（8）：1528－1535．］

［3］ MARIEM T，FEHMI H，PIERRE L．Project scheduling under resource constraints：application of the cumulative global constraint in a decision support framework［J］．Computers ＆Industrial Engineering，2011，61（2）：357－363．

［4］ CHEN Hao，JING Ning，LI Jun，et al．Method for changeable resources in electromagnetic detection satellites dynamic scheduling［J］．Journal of System Simulation，2009，21（24）：7833－7837（in Chinese）．［陈 浩，景 宁，李 军，等．一种适应资源变化的电磁探测卫星动态调度方法［J］．系统仿真学报，2009，21（24）：7833－7837．］

［5］ MOUHOUB M，SUKPAN A．Conditional and composite temporal CSPs［J］．Applied Intelligence，2012，36（1）：90－107．

［6］ ZHANG Lei，LIU Guangfu，HU Di，et al．Green product configuration design based on constraint satisfaction problems［J］．Journal of Mechanical Engineering，2010，46（19）：117－124（in Chinese）．［张 雷，刘光复，胡 迪，等．基于约束满足问题的绿色产品配置设计［J］．机械工程学报，2010，46（19）：117－124．］

［7］ ALDANONDO M，VAREILLES M，DJEFEL M．Towards an association of product configuration with production planning［J］．International Journal of Mass Customisation，2010，3（4）：316－332．

［8］ MITTAL S，FALKENHAINER B．Dynamic constraint satisfaction problems［C］//Proceedings of the 8th National Conference on Artificial Intelligence．Palo Alto，Cal．，USA：AAAI，1990：25－32

［9］ SCHIEX T，VERFAILLIE G．Nogood recording for static and dynamic constraint satisfaction problems［J］．International Journal of Artificial Intelligence Tools，1994，3（2）：187－207．［

10］ SABIN M．Towards more efficient solution of conditional constraint satisfaction problems［D］．Durham，Nh．，USA：U－niversity of New Hampshire，2003．

［11］ SABIN M，FREUDER E C，WALLACE R J．Greater efficiency for conditional constraint satisfaction［J］．Lecture Notes in Computer Science，2833，2003：649－663．

［12］ SABIN D，FREUDER E C．Configuration as composite constraint satisfaction［C］//Proceedings of the Artificial Intelligence and Manufaturing．Palo Ato，Cal．，USA：AAAI Press，1996：153－161．

［13］ ESTHER Gelle．Solving mixed and conditional constraint sat

isfaction problems［J］．Constraints，2003，8（2）：107－141．［14］ DONG Yang，DONG Ming，CHANG Xiaokun．A dynamic constraint satisfaction approach for configuring structural products under mass customization［J］．Engineering Applications of Artificial Intelligence，2012，25（8）：1723－1737．

［15］ WANG Lin，WEE－KEONG N G．Hybrid solving algorithms for an extended dynamic constraint satisfaction problem based configuration system［J］．Concurrent Engineering：Research and Applications，2012，20（3）223－236．

［16］ RAPHAEL F，BARRY O．Reasoning about conditional constraint specification problems and feature models［J］．Artificial Intelligence for Engineering Design，Analysis and Manufacturing，2011，25（2）：163－174．

［17］ BESSIERE C，MESEGUER P，FREUDER E C，et al．On forward checking for non－binary constraint satisfaction［J］．Aritficial Intelligence，2002，141（1/2）：205－224．

［18］ BESSIERE C，REGIN J C，YAP R H C，et al．An optimal coarse－grained arc consistency algorithm［J］．Artificial Intelligence，2005，165（2）：165－185．

［19］ BESSIERE C，STERGIOU K，WALSH T．Domain filtering consistencies for non－binary constraints［J］．Artificial Intelligence，2008，172（6/7）：800－822．

［20］ WOODWARD R J，KARAKASHIAN S，CHOUEIRY B Y，et al．Solving difficult CSPs with relational neighborhood consistency［C］//Proceedings of the Conference on Artificial Inteelligence．Palo Ato，Cal．，USA：AAAI Press，2011：112－119．

［21］ BESSIERE C，REGIN J C．Refining the basic constraint propagation algorithm［EB/OL］．［2012－05－06］．http：//citeseerx．ist．psu．edu/viewdoc/download？doi＝10．1．1．123．8012＆rep＝rep＆type＝pdf．

［22］ MITTAL S，FRAYMAN F．Towards a generic model of

configuration tasks［C］//Proceedings of the 10th International Joint Conference on Artificial Intelligence．San Fancisco，Cal．，USA：Morgan Kaufmann，1989：1395－1401．