汽车减速带的最优设置分析

杨光智,张 琛,张丹丰,赵 娜

(上海理工大学 材料科学与工程学院,上海 200093)

汽车减速带的最优设置分析

杨光智,张 琛,张丹丰,赵 娜

(上海理工大学 材料科学与工程学院,上海 200093)

为了更好地维护城市中小学门口的交通安全,合理设置校门口减速带,根据校门口区域车型和车速的限制条件,分析了减速带基本形状和减速带分布原理;将汽车轮胎视为刚体,对车轮通过一个圆弧形减速带的状况进行几何分析和动力学分析,建立了圆弧模型和减速带分布模型。通过实例求解,给出了最优的减速带设置方案。该方案可为城市中小学校门口设置减速带提供参考。

汽车减速带;圆弧模型;减速带分布模型

汽车减速带是为保障行人安全设置的一种交通设施,在遏制交通事故的发生中发挥了重要的作用。目前减速带的类型有道钉减速带、圆弧式(驼峰式)减速带、水泥台减速带、热塑振动减速带、路面凹槽减速带、沥青混合料减速带、防滑减速带、卵石减速带等,不同减速带的使用条件不同[1]。

汽车减速带减速的基本原理是在公路特殊路段的行车道上设置某种突起设施,对车辆驾驶员起到警示作用,车辆驾驶员根据常识预计到车辆通过减速带时会带来车辆剧烈振动,从而促使车辆驾驶员自觉、主动地降低车速,达到提高特殊路段行车安全性的目的[2]。同时减速带也可对行人起到警示作用,防止交通事故的发生。

随着经济的发展,人民生活水平不断提高,城市私家车数量日渐增加,这给本已拥挤的道路交通带来新的问题。值得关注的是,城市绝大多数中小学校门都面临街道路口,每当上学、放学时段,人、车混杂,险象环生,加上道路上车辆车速快,极易造成未成年人道路交通伤害事故。因此,在中小学校门口合理设置减速带,对确保学校师生道路交通安全非常重要。基于中小学校门行驶的车辆主要为小型车辆,笔者选取圆弧形减速带为研究对象[3-4],用数学分析的方法,通过简化条件建立圆弧模型、减速带分布模型,以定量分析其减速效果,进而给出最优的减速带设置方案。

1 汽车减速带设置数学模型

1.1 减速带形状的选取

对于不同车型,减速带形状选取考虑的因素不同。对大型货车而言,更重的是考虑它的安全性;相对于小车来讲,其舒适性、平稳性、低噪音性更被人们所看重。根据ADAMS/CAR模拟减速带研究结果,对于大型货车较多的路段,选择抛圆相切的横断面形状的减速带;而对于小车较多的路段,应选择圆弧形横断面形状的减速带[3-4]。由于中小学校门口行驶的车辆主要为小型车辆,因此笔者选取圆弧形减速带作为研究对象。

1.2 圆弧模型的建立

假设减速带截面的形状为圆弧形,车辆在过减速带时保持水平方向的速度不变,视减速带与车轮的碰撞为完全弹性碰撞,车轮和车胎为刚体,忽略其在碰撞过程中的变形,忽略一切摩擦损耗。

为了驾驶的安全,设在整个过程中车胎始终与减速带保持良好的接触。通过对车轮与减速带几何分析,利用运动方程求解出速度v、加速度a与横截面高度h和横截面宽度b的关系。

设驾驶员距减速带20 m处看到减速带,并以制动减速度a1进行减速至临界速度vc,以临界速度vc通过减速带。此时减速带与汽车轮胎的接触状态如图1所示。这里,临界速度vc指汽车通过减速带时轮胎不脱离时的最大速度。

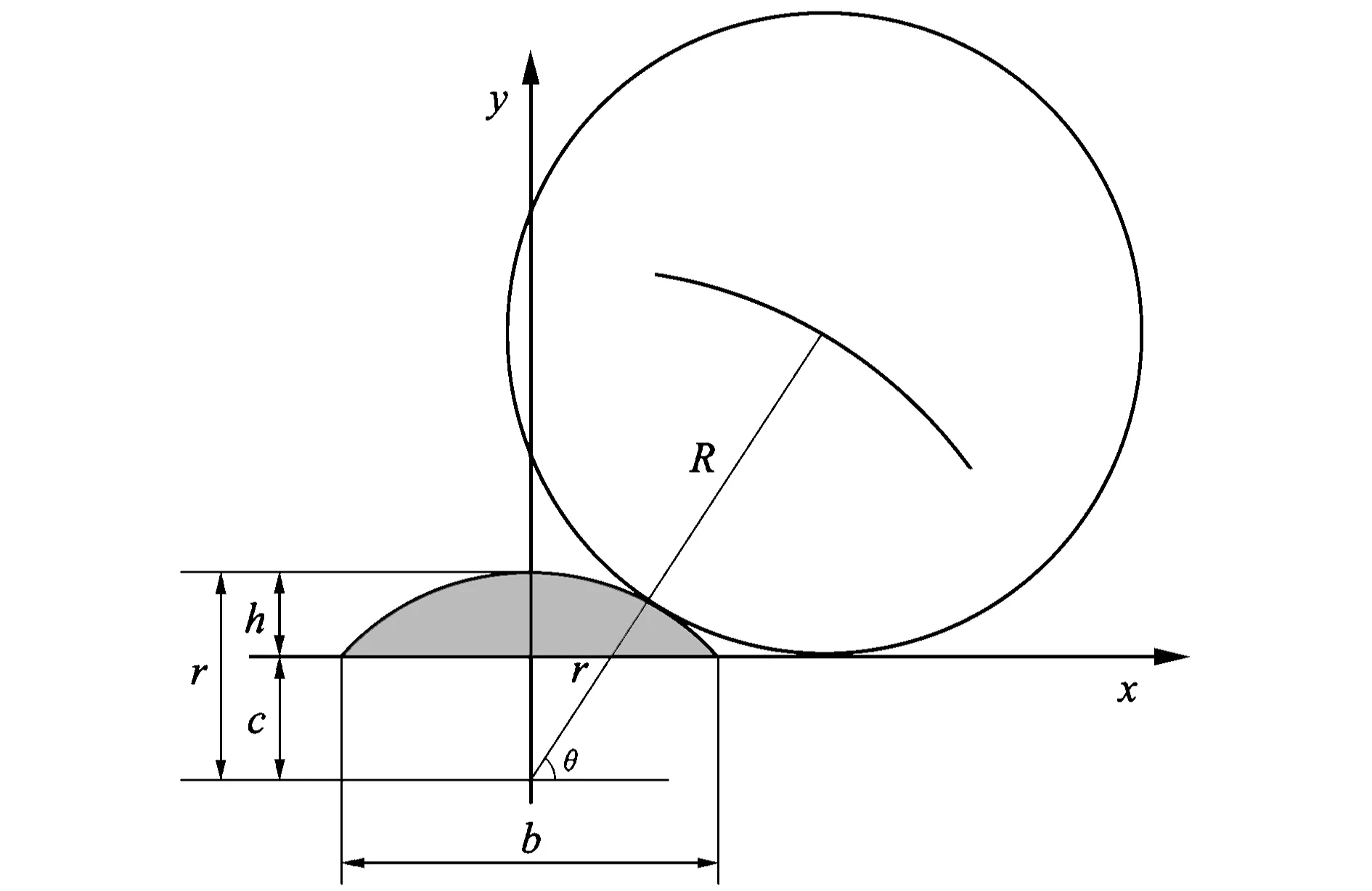
r—减速带圆弧半径,mm;R—汽车轮胎外胎半径,mm;h—圆弧形减速带横截面的高度,mm;b—圆弧形减速带横截面的宽度,mm;c=r-h,mm

由图1减速带与汽车轮胎接触状态的几何分析可知:

化简后得

由

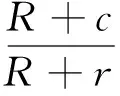
得

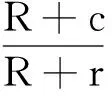
当汽车轮胎从圆弧形减速带滚过时,轮轴的运动轨迹方程为:

x2+(y+c)2=(R+r)2,

求解汽车轮胎从圆弧形减速带上面滚动t秒后,轮轴的运动轨迹方程,得:

对t求导得轮轴速度:

vx=-vc,

vy=vc[(R+r)cosθ-vct]{(R+r)2-

[(R+r)cosθ-vct]2}-1/2.

再对t求导得轮轴加速度:

ax=0 ,

ay=-vc2{(R+r)2-

[(R+r)cosθ-vct]2}-1/2-

vc2[(R+r)cosθ-vct]2{(R+r)2-

[(R+r)cosθ-vct]2}-3/2.

为了保障安全,当车通过减速带时,要求ay≤g(重力加速度),且vy=0,则,临界速度为:

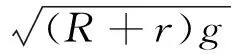
(1)

1.3 减速带分布模型的建立

从汽车动力学的角度出发,以车速不超过道路目标车速为前提[5],建立圆弧形减速带设置间距理论模型。设:

1) 司机在未看到减速带之前做匀速v0直线运动,司机在距离第一条减速带20 m时看到减速带后,开始以一定的制动减速度a1进行减速至临界速度vc,并以临界速度通过减速带;

2) 汽车通过减速带时的水平速度恒定;

3) 忽略过减速带时间;

4) 忽略减速带的带宽;

5) 忽略汽车的车长;

6) 通过减速带后汽车以制动加速度a2进行匀加速直线行驶。

这里,v0为司机在看到减速带之前做匀速直线运动的初速度,m/s。司机在看到减速带后,汽车的减速效果通过减速系数ε衡量,即:

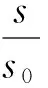
式中:s为设置减速带后从开始减速到恢复原速汽车行驶的路程,m;s0为未设置减速带时,汽车行驶的路程,m。

若汽车通过减速带后加速到的最大速度超过限定速度,则ε越小减速效果越好;如汽车通过减速带后加速到的最大速度未超过限定速度,则ε越大减速效果越好。

图2是汽车通过一个减速带时,速度与时间关系的示意图。

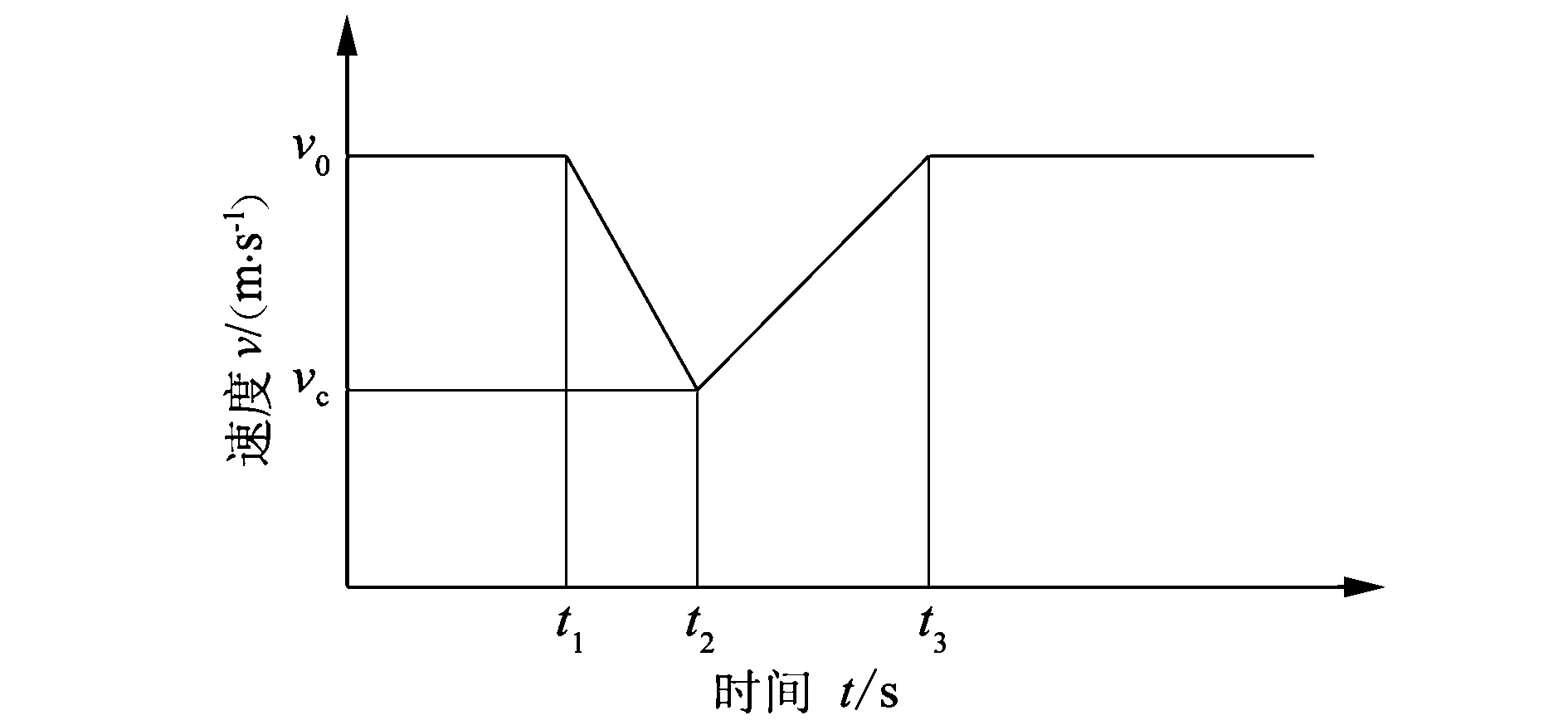
图2 汽车通过一个减速带时速度与时间关系

设置减速带后,汽车在t1～t3时间内行驶的路程为:

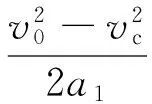
在未设置减速带的情况下,汽车在t1～t3时间内行驶的路程为:

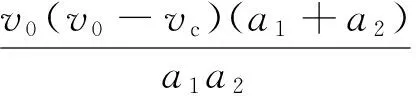
即可得出汽车通过一个减速带的减速系数ε为,

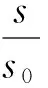
若等距设置n个减速带,则汽车从第一次减速开始到恢复原来速度v0这段时间内(t1～t2n+1)所行使的路程为:

式中:v′为通过一个减速带后,在下一次减速前(准备通过下一个减速带)汽车加速所能达到的最大速度,如图3所示。

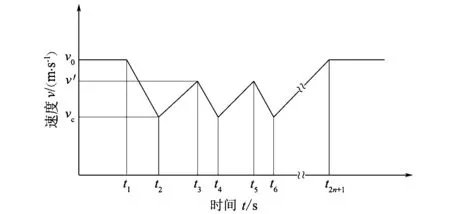
图3 汽车通过n个减速带时速度与时间的关系

在未设置减速带时,汽车在时间t1～t2n+1内匀速行使的路程为:

则,汽车在时间t1～t2n+1内减速系数为:

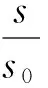
(2)

相邻两条减速带之间的距离L1:

(3)

得出,

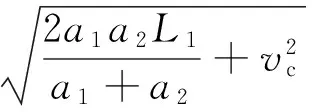
(4)

值得一提的是,由于在建模过程忽略轴距(车长),因此实际相邻两条减速带之间的距离应为L1+L2(轴距)。

设,相邻两条减速带之间的实际距离为L,轴距为L2, 则L=L1+L2, 如图4所示。

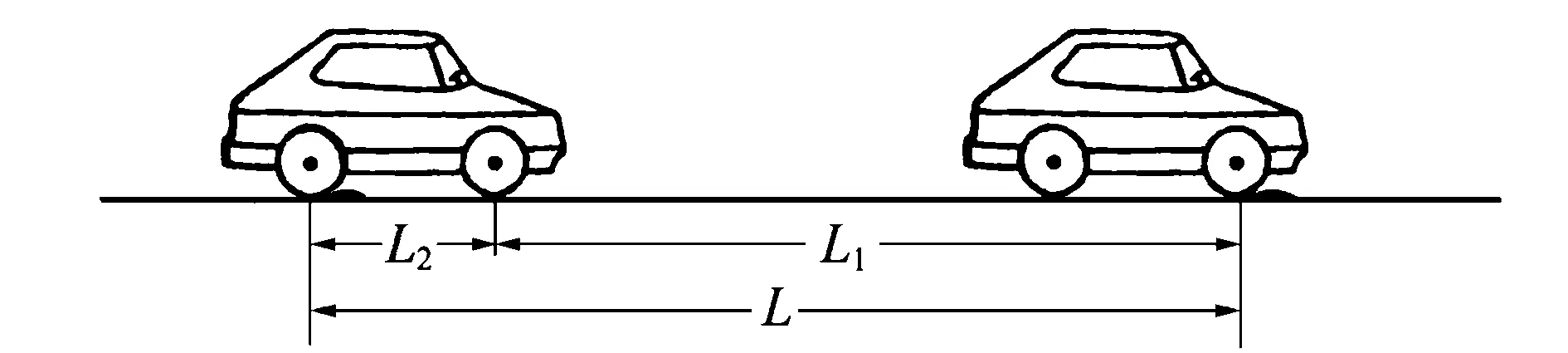
图4 相邻两条减速带之间的距离

2 实例分析

2.1 问题提出

某小学所在路段为双向车道,全天限速40 km/h,仅限小型车辆通行。在早晨上学和下午放学时间,家长和学生在校门口形成人流高峰,虽有交通协管员维护秩序,但来往车辆仍然对学生和家长安全形成威胁。为维护校门口的安全与秩序,学校考虑协同交管部门,决定在该路段设置减速带,使校门口左右各30 m范围内,车速控制在15 km/h以内,达到控制来往车辆速度,保障行人安全的目的。

2.2 问题求解

按照商业圆弧形减速带型号及其规格(表1),采用已建立的圆弧模型进行计算,选择适宜用于小学校门口设置减速带的型号。

表1 几种常用的圆弧形减速带型号及其规格[6]

基于式(1),采用软件EXCEL2013算出的各种型号减速带相应的临界速度vc,计算结果列入表2。这里取汽车轮胎外胎半径R=320 mm。

表2 各种型号圆弧形减速带相应的临界速度

从表2可看出，圆弧A型减速带的vc=2.53 m/s,减速效果最好。

考虑到汽车通过该路段的实际情况——司机希望快速通过该路段,基于正常行驶(未设置减速带的路段)限速40 km/h规定,得v0=11.11 m/s;依据汽车在校门口(设置减速带的路段)的限速15 km/h,可得v′≤4.17 m/s。

设,汽车通过等距分布的圆弧A型减速带时,制动减速度a1=5 m/s,制动加速度a2=2.5 m/s,小车平均车长4.5 m。

已知,vc=2.53 m/s;要求,v′≤4.17 m/s。以轮胎为基准,由式(3)算出相邻两条减速带之间的距离为:

实际相邻两条减速带之间的距离应为:

L+4.5=3.3+4.5=7.8 (m).

需要设置减速带的条数为:

(n-1)×L=60 m,n=8.69(条).

因此,此路段上等距离设置9条减速带较为合理。

利用autoCAD(2008)软件作出小学校门口减速带设置分布示意图(图5)。

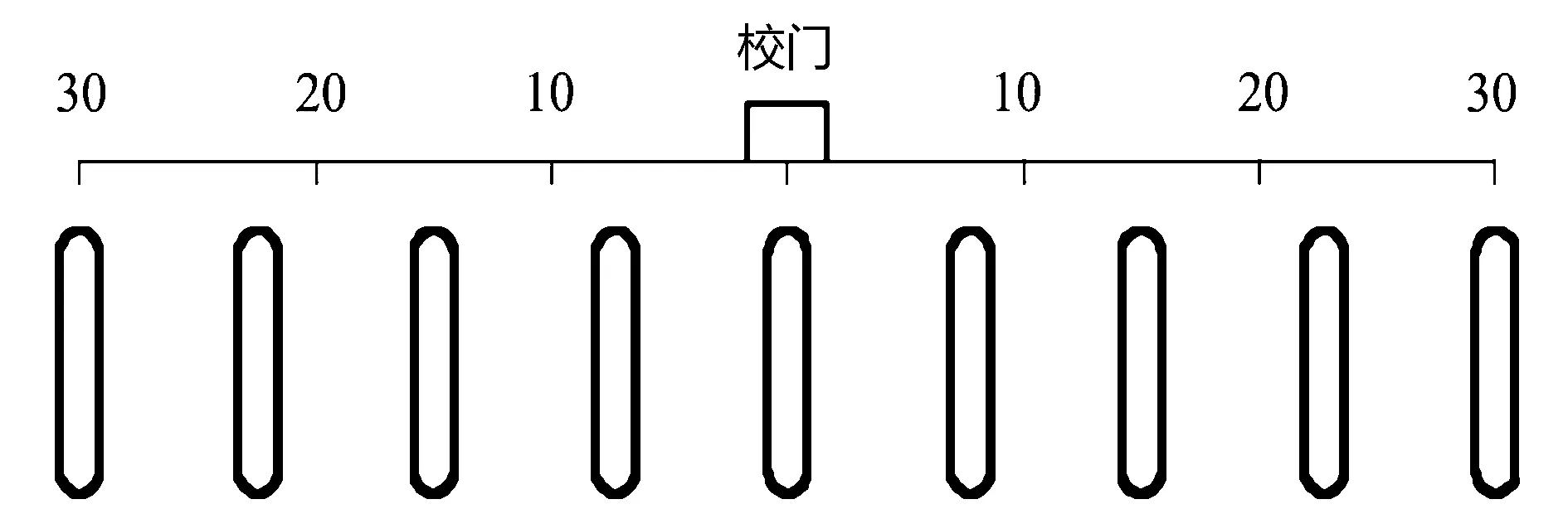
图5 小学校门口减速带设置分布示意图

依据式(2),采用MATLAB(R2010a)作出的圆弧A型减速带条数n与减速系数ε的关系曲线如图6所示。

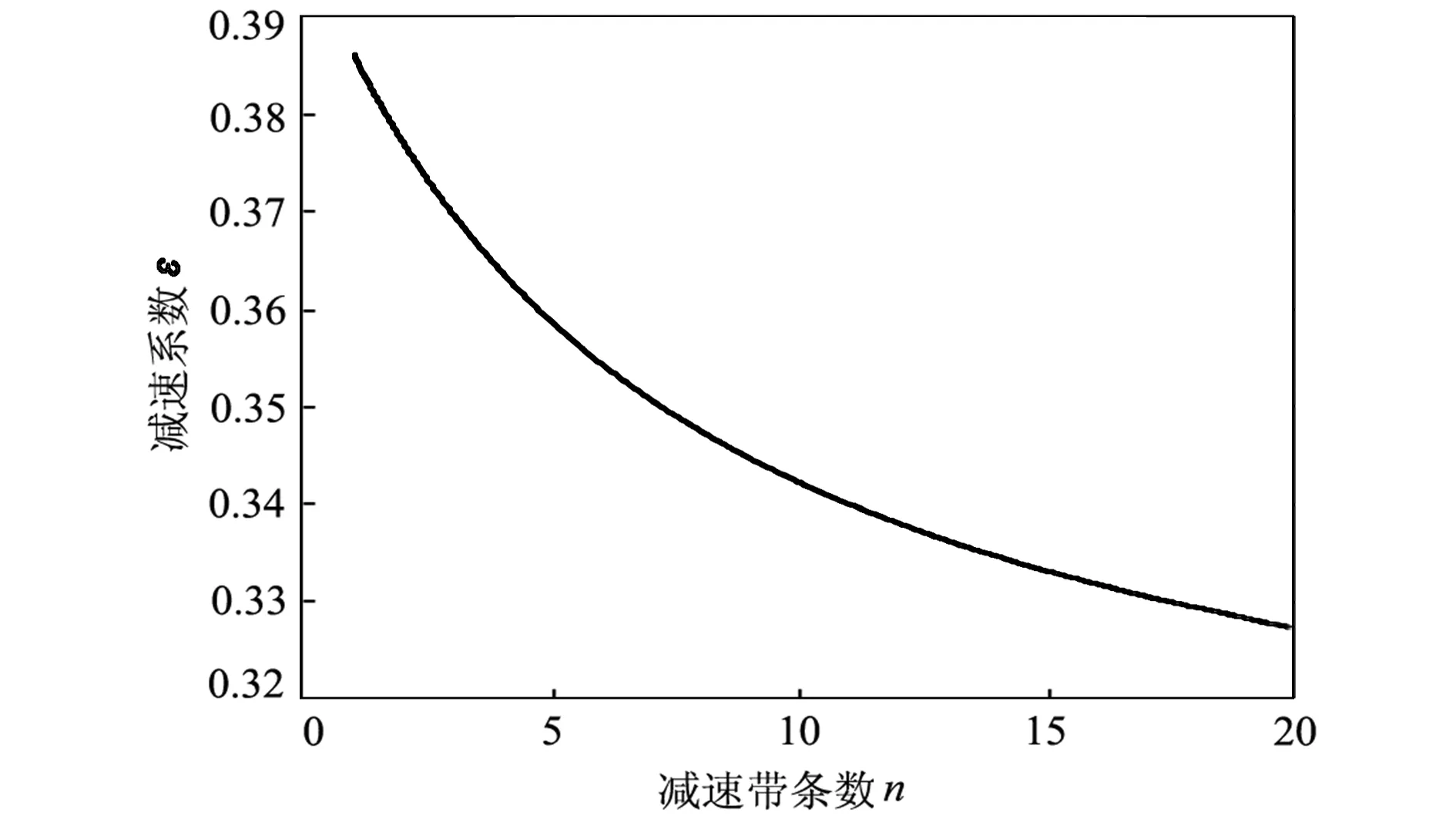
图6 圆弧A型减速带条数与减速系数的关系曲线

由图6可以看出,当圆弧A型减速带条数n=9时,减速系数ε=0.345。可求得,设置减速带后,汽车在校门口左右各30 m范围内的行驶速度v′=40×0.345=13.8 (km/h),达到小学校门口限速15 km/h内的要求。

3 结束语

将轮胎视为刚体,对车轮通过一个圆弧形减速带的状况进行了几何分析和动力学分析后,建立了圆弧模型和减速带分布模型,并利用MATLAB(R2010a)、autoCAD(2008)、EXCEL2013等软件进行求解,得出:在小学校门口左右各30 m范围内设置9条圆弧A型减速带,即可将汽车40 km/h的行驶速度减速为13.8 km/h,达到小学校门口限速15 km/h内的要求。

[1] 李家顺,李淑庆,钱小兵. 减速带在校园交通安全的应用研究[J].交通信息与安全,2011,29(1):64-67.

[2] 杨英武,韩舟轮,王柏生.车辆通过减速带引起的振动分析[J].振动工程学报,2007,20(5):502-506.

[3] 邱望标,黄克,黎熊,等. 减速带形状对汽车振动的影响分析[J]. 橡胶工业, 2008,55(11):675-679.

[4] 黎 熊,刘 彩,邱望标. 道路减速带形状对车辆平顺性影响的研究[J]. 轮胎工业, 2010, 30(1): 54-56.

[5] 许源,朱顺应,彭武雄,等. 基于汽车动力学的震动减速带设置间距研究[J].交通科技,2008(1):101-102.

[6] 李莉娅. 驼峰减速带带宽比对汽车座椅垂直方向上加速度影响研究[J].科技创新导报,2010(19):78-79.

(编辑：庞富祥)

AnalysisofVehicleDecelerationStripOptimalSetting

YANGGuangzhi,ZHANGChen,ZHANGDanfeng,ZHAONa

(SchoolofMaterialsScienceandEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

In order to keep traffic safety near schools, we analyzed the shape of deceleration strip and theory of deceleration strip distribution under specific assumptions. Through the geometrical analysis and dynamic analysis of arc deceleration strip, we set up arc mathematical model and deceleration strip distribution model. Furthermore we provided the best distribution scheme according to an example, which can be a reference of setting deceleration strip near schools.

arc deceleration strip;arc mathematical model; deceleration strip distribution model

2013-06-11

杨光智(1977-),男,陕西渭南人,工学博士,硕士生导师,主要从事城市及环境功能材料的研究，(Tel)021-55271689， (E-mall)yanggzh@usst.edu.cn

1007-9432(2014)01-0123-05

U412.12

:A