顶底复吹条件下不锈钢VOD精炼过程的数学模拟——过程数学模型

魏季和，李 毅

(上海大学 材料科学与工程学院,上海 200072)

顶底复吹条件下不锈钢VOD精炼过程的数学模拟
——过程数学模型

魏季和，李 毅

(上海大学 材料科学与工程学院,上海 200072)

对顶底复吹条件下不锈钢VOD精炼过程提出了一个数学模型。该模型假设低压下顶吹入的氧,部分与逸出熔池的CO反应,部分使生成的钢液滴内各元素氧化,其余经射流冲击坑向钢液渗透和溶解;进入熔池的氧使钢中的碳、铬、硅、锰和铁氧化,生成的FeO是一中间产物。所有可能的氧化-还原反应分别在钢液/熔渣及钢液/气泡界面同时发生,并在竞争中达到其各自的综合平衡。在较高碳含量下,各元素氧化速率主要与吹氧量有关;在低碳含量下,脱碳速率主要取决于钢中碳的传质。吹入钢液未反应的氧不在钢中溶解和积聚,逸出熔池并参与熔池上方炉气内CO的二次燃烧。以多层复合壁的二维瞬态导热处理了炉壁传热,考虑了各操作因素及不等温状态等的影响。

不锈钢;VOD精炼;顶底复吹过程;数学模拟

与不锈钢侧顶复吹AOD精炼一样,顶底复吹条件下的不锈钢VOD精炼也是一个复杂的多相火法冶金过程。由于精炼反应在低压下进行,它可在较低的初始碳含量和温度下不使铬大量氧化，而使碳降至更低的水平,广泛用于超低碳和超低碳氮不锈钢的生产。关于不锈钢VOD精炼过程的数学模拟研究,文献中现有的工作为数不多[1-3]。Ding等[1]基于精炼反应的热力学和动力学,通过逐步比较反应Gibbs自由能计算气-金反应中氧的分布,建立了一个可随钢液、气体和渣量变化，持续估算精炼过程的VOD数学模型。但是,有关参数值的可靠性直接影响该模型的计算精度。Kitamura等[2]针对VD脱氮和脱碳过程提出了相应的数学模型,并用以分析VOD精炼过程,估算了脱氮和脱碳反应在各反应位置的比例。他们将各反应区的传质系数均取为常数,也未考虑搅拌对传质的影响。笔者对顶底复吹条件下不锈钢VOD精炼过程作了数学模拟研究。注意到该过程的物理和化学特性,包括其热力学和动力学特征,考虑到体系的热量和质量衡算,以及各操作因素等的影响,研制和提出了相应的数学模型。应用该模型处理和分析了120 t VOD炉内20炉409L型铁素体不锈钢的整个精炼过程,基于该模型的估计考察了各有关因素的影响及精炼工艺的优化。本文给出该模型的有关细节。

1 精炼过程数学模型

1.1 模型的基本假设

对顶底复吹条件下不锈钢VOD精炼过程提出如下基本假设。

1) 在真空条件下，经顶枪吹出的氧气,一部分与自熔池逸出的CO在熔池上方气相内发生反应,一部分使从熔池溅出的钢液滴内的各元素氧化,其余部分通过由冲击射流在熔池表面形成的凹坑向钢液渗透和溶解。

2) 进入熔池的氧使溶于钢液的C、Cr、Si、Mn、Fe等同时氧化,生成的FeO立即被还原,是精炼过程中的一个中间产物。

3) 在顶底复吹过程中,所有可能的氧化-还原反应分别在钢液/熔渣和钢液/气泡界面同时发生,并在竞争中达到各自的综合平衡;在停止吹氧后的底吹氩过程中,各精炼反应主要在钢液/气泡界面同时发生,并在竞争中达到一综合平衡,精炼过程中总的速率为顶吹过程和底吹过程两者的贡献之和。在还原期,熔渣中各氧化物和钢中各元素在钢液/熔渣界面达到一新的综合平衡。

4) 在较高碳含量下,各元素的氧化速率主要与供氧速率有关;在低碳浓度下,脱碳速率主要决定于钢液中碳的传质。

5) 精炼过程中脱氮、脱氢速率的控制环节是钢液内N、H的传质。

6) 整个精炼过程中熔池的温度和成分连续发生变化,且在任何时刻都均匀分布。

7) 除C、Cr、Si、Mn外,溶于钢中的其他元素的氧化损失不予考虑。

1.2 精炼反应图式

1) 氧化-还原反应。由溶于钢液的C、Cr、Si、Mn和作为钢基体的Fe的直接氧化可得该体系内式(1-4)和(5-8)两组独立平衡,

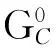
(1)

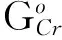
(2)

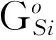
(3)

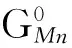
(4)

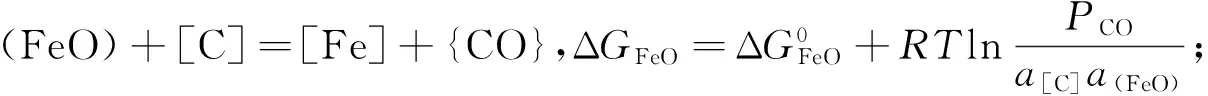
(5)

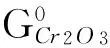
(6)

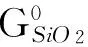
(7)

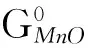
(8)

2) 脱氮反应

(9)

3) 脱氢反应

(10)

1.3 过程速率方程

顶底复吹条件下不锈钢VOD精炼过程的速率方程，包括脱碳和脱气(氢和氮)的速率方程以及所考察的有关元素的氧化或还原过程的速率方程。

在较高碳含量下(相应的吹炼时间为tH),各元素的氧化速率分别为:

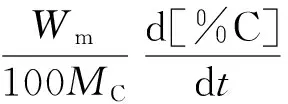
(11)

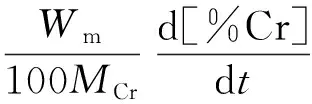
(12)

(13)

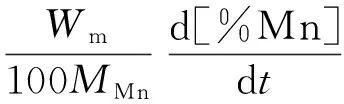
(14)

Ar气泡表面的脱碳速率为:

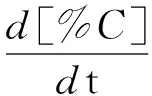
(15)

由此,较高碳浓度下总的脱碳速率为:

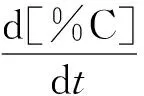
(16)

在低碳含量下(相应的吹炼时间为tL=tT-tH)),顶吹氧过程的平均脱碳速率为:

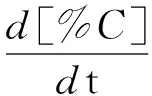
(17)

由该式与式(15),在低碳水平下相应的总平均脱碳速率为:

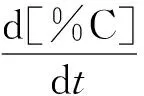
(18)

这时,精炼反应主要为C和Cr的竞争性氧化。考虑如下反应:

(Cr2O3)+3[C]=2[Cr]+3{CO}.

(19)

对低碳水平下的顶吹氧脱碳过程,有下式成立:

(20)

对从底部吹入的Ar的脱碳过程,注意到Ar和生成的气体对CO的稀释作用,

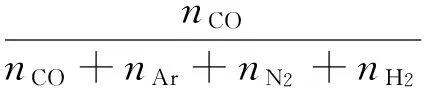
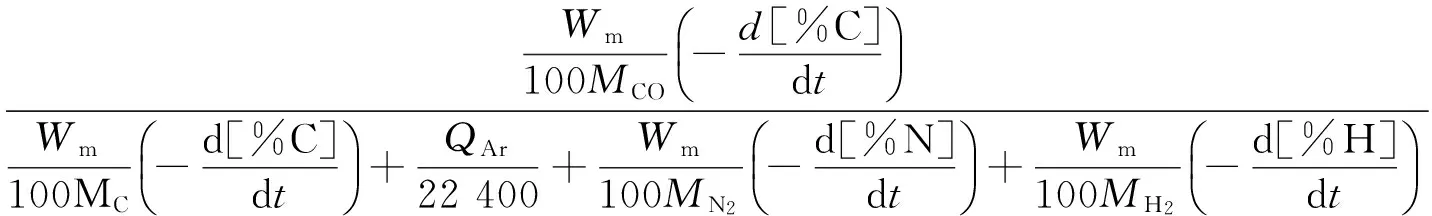
(21)

相应的速率为:

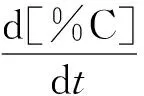
(22)

其中:

(23)

(24)

由此,式(18)可改写为:

.

(25)

对停止吹氧后的真空处理期(相应的吹炼时间为tZ),其平均脱碳速率也由式(22)-(24)给出。

按式(5)-(8),由脱碳速率可得钢液内Cr, Si和Mn浓度的变化速率为:

(26)

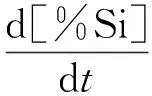
(27)

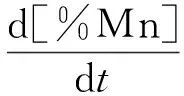
(28)

对式(9)所示的精炼过程中的脱氮,有:

(29)

其中

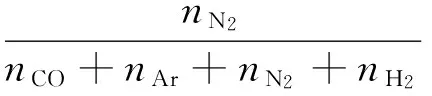
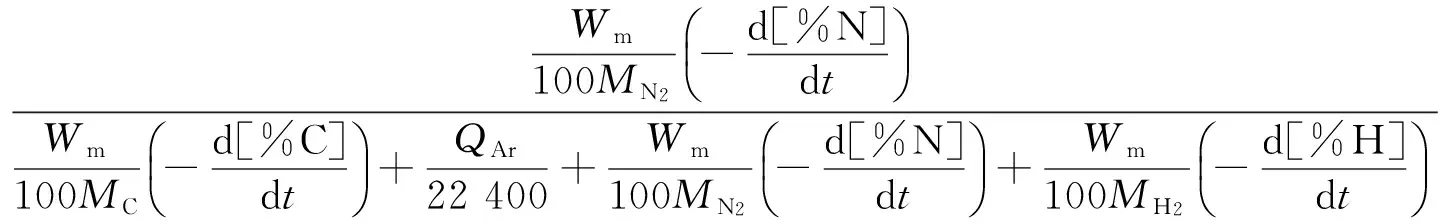
(30)

将式(30)代入式(29),得:

(31)

由此可有:

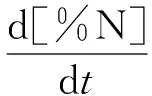
(32)

式中:

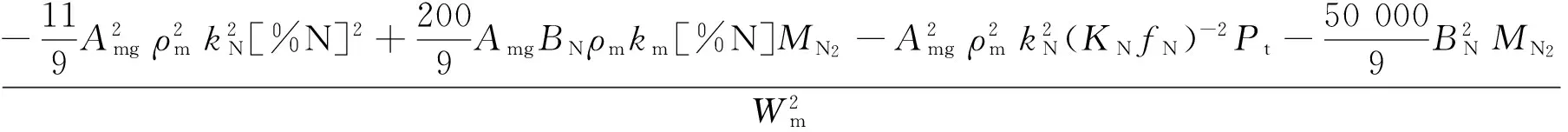
(33)

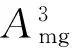
(34)

(35)

对式(10)所示的精炼过程中的脱氢,则有

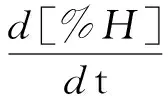
(36)

式中:

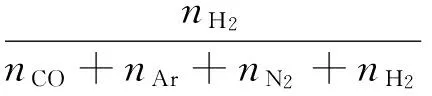
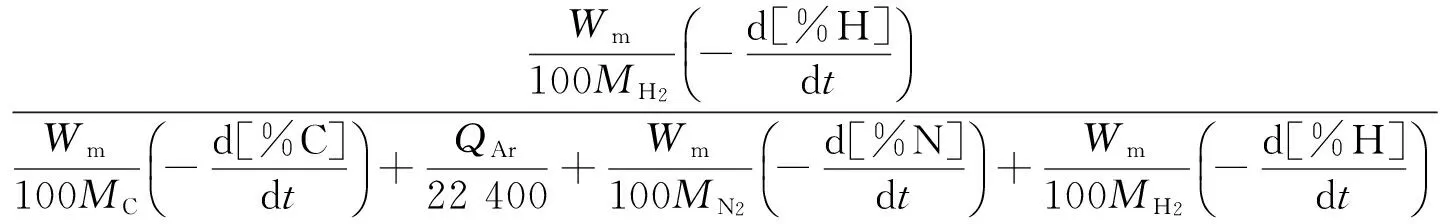
(37)

将式(37)代入式(36),有:

(38)

由此可得:

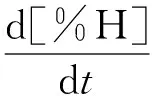
(39)

其中:

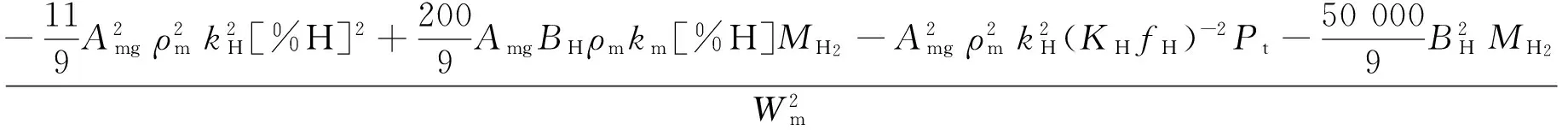
(40)

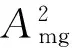
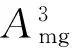
(41)

(42)

1.4 炉衬内的温度分布

本工作按多层复合壁的二维瞬态导热分析和处理了炉体的传热特性。将炉体分为上部(不与熔体接触的部位)、下部(渣线以下位置)和炉底三部分,对每部分耐火炉衬和炉壳内的温度分布都满足下式:

(43)

在实际过程中,炉体与钢液和周围环境的热交换相当复杂,必须按不同部位确定相应的边界条件。在炉内,炉壁与钢液直接接触,可认为其内表面温度等于钢液温度。本工作对炉身下部和炉底均取第一类边界条件;对熔池液面以上的区域和炉壳外表面,采用第三类边界条件,并将由对流和辐射引起的传热系数分别折合成一综合的换热系数。据此,对应于式(43),不同部位的初始条件分别为:

对钢液,

Tm=T0;

(44)

对炉体上部,

Tref(x,y,0)=Trefu10;Tref(x,y,0)=Trefu20;

(45)

对炉体下部,

Tref(x,y,0)=Treft10;Tref(x,y,0)=Trefd20;

(46)

对炉体底部,

Tref(x,y,0)=Trefb10;Tref(x,y,0)=Trefb20.

(47)

相应的边界条件分别为:

对炉壳外表面,

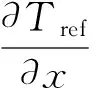
(48)

对炉体上部,

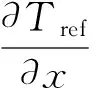
(49)

对炉体下部和底部,

Tref(x,y,t)=Trefm.

(50)

式(45)-(50)中x和y的取值范围根据实际体系而定。在给出的定解条件下求解方程(43)可得炉衬及炉壳内的温度分布,从而可为体系的热量衡算提供必要和可靠的信息及基础。

1.5 体系的热量衡算

考虑全部热量输入和输出以及积累,可得该体系的如下热量衡算方程:

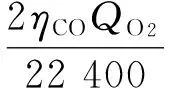
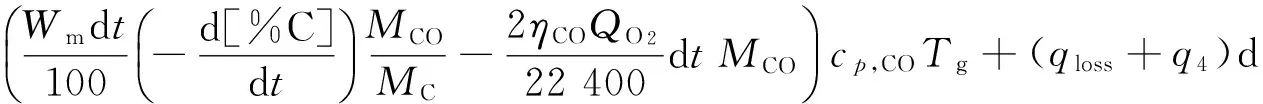
(51)

相应地,熔池升温速率为:

(52)

1.6 模型的初始条件和边界条件

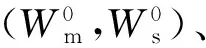
2 模型参数的确定

本工作依然采用以往所作的计算[7-8]确定吹入的氧在溶于钢液的各元素间的分配率(xi)和渣中各氧化物的“供氧率”(xio)[4, 9-12],即两者正比于界面处氧化和还原反应的Gibbs自由能。据此,对各元素的氧化,有:

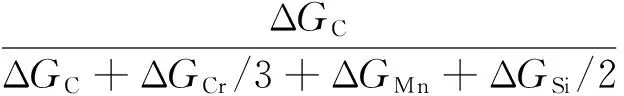
(53)

(54)

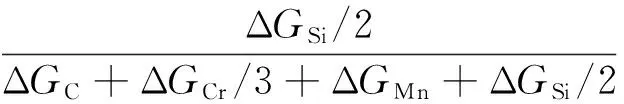
(55)

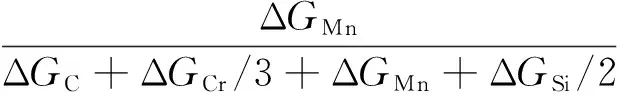
(56)

对各氧化物的还原,有:

(57)

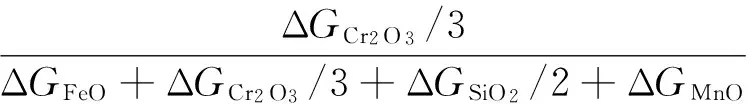
(58)

(59)

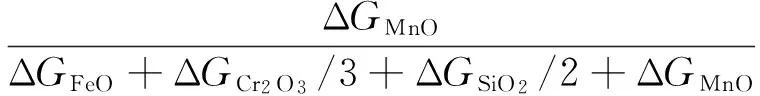
(60)

此外,基于我们以往的研究[4, 7-18]和文献中有关工作[19],确定了钢液和熔渣中各组分的活度,各精炼反应的平衡常数和标准Gibbs自由能,钢液内碳、氮、氢的传质系数,各元素的氧化焓,经三孔氧枪顶吹和经三枪底吹过程中反应界面面积等参数。据实际情况，取定了各种耐火材料和炉壳(钢板)的导热系数及各有关物质的密度和比热等物理常数。参照文献[20]给出的结果,并考虑低压环境,确定了与炉体各部分相关的综合传热系数。由现有结果[21]和复吹VOD熔池内流体流动特性[6],根据各添加剂加入量和加入时熔池温度合理确定了相应的熔化时间,即其冷却效应的持续时间。基于文献[22]的数据,取定了主吹和动吹各期顶吹氧气的利用率和相应的二次燃烧利用率。

3 模型的数值解

基于PHOENICS软件,编制了求解该模型的计算机程序。在开始计算前,先判别是否有顶吹氧操作。如果处于氧化精炼期,由计算得的钢液内各元素氧化反应的Gibbs自由能确定相应的氧气分配率。随后分别计算取决于氧气流量的脱碳速率(dC1/dt)和由钢液内碳的传质控制的脱碳速率(dC2/dt)。比较这两个速率,如果|dC1/dt|<|dC2/dt|,则以|dC1/dt|求钢液内其他元素的氧化速率。反之,以|dC2/dt|计算耗于脱碳的氧量,由剩余氧量及相应的氧气分配率计算铬、硅、锰的氧化速率。然后,求解炉衬温度场,由所得炉衬各部位的温度分布及其热损和体系热量衡算熔池升温速率,并由数值积分得到新的钢液成分和温度,继而再次计算炉衬的温度场。二者相互影响,交替变换。对炉衬温度场的求解,以控制体积法将泛定方程(43)及其定解条件 (式(44)-(50)) 离散化,整个计算域的网格划分为37×128。由体系质量衡算可确定熔渣各组分的浓度。对停止供氧后的还原精炼期,先计算各氧化物还原反应的Gibbs自由能,然后计算渣中各氧化物的供氧率以及(dC2/dt),以求得其还原速率。最后,按同样的步骤和程序计算熔池升温速率以及钢液及渣中各组分的浓度。鉴于FeO被视为吹氧过程的中间产物,其在体系质量及热量衡算中的影响可予忽略。该模型的输出结果包括钢液和熔渣的成分、温度和质量,氧在各元素间的分配率和各氧化物的供氧率,脱碳速率以及炉衬内的温度分布等随精炼时间的变化。

该模型可用以分析顶底复吹条件下不锈钢的整个精炼过程,包括氧化和还原过程。应用该模型于120 t顶底复吹VOD炉内28炉409L型铁素体不锈钢的精炼;基于模型估计考察了各有关因素的影响和吹炼工艺的优化。所得结果将在另文中予以报道[23]。

附：主要符号表

A—反应界面面积，cm2;

agro—炉壳外表面的传热系数, J·cm-2·s-1·K-1;

agru—炉身上部内衬传热系数, J·cm-2·s-1·K-1;

ai—组分i的活度;

[%i]—钢液中组分i的质量分数, %;

[%i]e—反应界面处钢液中组分i的平衡质量分数,%;

cp,i—物质i的等压比热, J·g-1·K-1;

fi—钢液中i组分的Henrian活度系数 ;

ΔGi—物质i的吉布斯自由能, J·g-1;

ΔHi—元素i的氧化焓, J·g-1;

KCr-C—碳还原氧化铬反应的平衡常数 ;

ki—钢液中元素i的传质系数, cm·s-1;

Mi—物质i的摩尔质量, g·mol-1;

ni—单位时间内组分i的摩尔数, mol·s-1;

Pi—气体i的无量纲分压;

Pt—熔池内的无量纲总压 ;

PV—真空室内的无量纲压力 ;

Qi—气体i的流量, cm3·s-1;

q1—炉体上部的传导热损, J·s-1;

q2—炉体下部的传导热损, J·s-1;

q3—炉底的传导热损, J·s-1;

q4—熔池升温过程中耐火材料吸热, J·s-1;

qloss—炉体总热损, J·s-1;

qu—体系不确定热损,J·s-1;

R—气体常数(=8.314), J·mol-1·K-1;

Sr—与体系热衡算有关的源项 ;

T—熔池温度, K ;

Tf—环境温度, K ;

Tg, Tg0—气体温度及其初始值, K ;

Tref—炉衬温度, K ;

tH—脱碳临界点以前的供氧时间, s ;

tL—脱碳临界点以后的供氧时间, s ;

tT—顶枪总供氧时间, s ;

tZ—停止供氧后的真空处理及还原时间, s ;

Wi—物质i的质量, g ;

x—直角坐标, cm ;

xi—氧对元素i的分配率 ;

xiO—元素i的氧化物对碳的供氧率 ;

y—直角坐标, cm ;

η—氧气利用率 ;

ηCO—顶吹氧气中用于二次燃烧部分所占的比率 ;

λi—物质i的导热系数, m·cm-1·K-1;

ρi—物质i的密度, g/cm3;

下标:mg, ms—钢液/气泡和钢液/熔渣界面 ;

g, m—气体和钢液 ;

ref, s—炉衬和熔渣 ;

u, l, b—炉衬的上部, 下部, 底部 ;

1, 2, 0—炉衬各部的上, 下截面,初始态

[1] Ding R,Blanpain B,Jones P T,et al.Modeling of the Vacuum Oxygen Decarburization Refining Process [J]. Metall Mat Trans B, 2000,31(2): 197-206.

[2] Kitamura T,Miyamoto K. Mathematical Model for Nitrogen Desorption and Decarburization Reaction in Vacuum Degasser [J]. ISIJ Int, 1996, 36(4): 395-401.

[3] Reichel J, Szekely J. Mathematical Modeling and Experimental Verification in the Decarburization of Industrial Scale Stainless Steel Melts [J]. Iron & Steelmaker, 1995(5): 41-48.

[4] Zhu Hong-Li, Wei Ji-He,Shi Guo-Min, et al.Preliminary Investigation of Mathematical Modeling of Stainless Steelmaking in an AOD Converter: Mathematical Model of the Process [J]. Steel Research Int, 2007, 78(4): 305-310.

[5] Fruehan R J. Fundamentals and Practice for Producing Low Nitrogen Steels [J]. ISIJ Int, 1996, 36(Sup): 56-61.

[6] Wei Ji-He，Zeng Lin. Numerical Simulation of Fluid Flow in Bath during Combined Top and Bottom Blowing VOD Refining Process of Stainless Steel [J]. Steel Research Int, 2012, 83(11): 1053-1070.

[7] Wei Ji-He,Zhu De-Ping. Mathematical Modeling of the Argon-Oxygen Decarburization Refining Process of Stainless Steel: Part 1. Mathematical Model of the Process [J]. Metall Mater Trans B, 2002, 33(1): 111-119.

[8] Wei Ji-He，Zhu De-Ping. Mathematical Modeling of the Argon-Oxygen Decarburization Refining Process of Stainless Steel: Part 2. Application of the Model to Industrial Practice [J]. Metall Mater Trans B, 2002, 33 (1): 121-127.

[9] Wei Ji-He,Cao Ying,Zhu Hong-Li,et al. Mathematical Modeling Study on Combined Side and Top Blowing AOD Refining Process of Stainless Steel [J]. ISIJ Int, 2010,51(3): 365-374.

[10] Shi Guo-Min,Wei Ji-He,Zhu Hong-Li,et al.Preliminary Investigation of Mathematical Modeling of Stainless Steelmaking in an AOD converter: Application of the Model and Results [J]. Steel Research Int, 2007, 78(4): 311-317.

[11] 曹英. 侧顶复吹条件下不锈钢AOD精炼过程的数学模拟[D]. 上海: 上海大学, 2005.

[12] 舒杰辉. 不锈钢侧顶复吹AOD精炼过程数学模拟研究[D]. 上海: 上海大学, 2004.

[13] Wei Chi-Ho (Wei Ji-He)，Mitchell A. Changes in Composition during A C ESR [C].Proc 3rdProcess Technology Conf，AIME, AISE, Warrendale, PA, USA, 1982(3)：232-254.

[14] Wei Ji-He， Mitchell A. Changes in Composition during A C ESR.: Theoretical Mass Transfer Model and Laboratory Results and Analysis [J]. Chin J Metal Sci Technol, 1986, 2(1): 11-31.

[15] 魏季和, Mitchell A. 工业规模电渣重熔过程的传质模型分析 [J]. 金属学报, 1987, 23(3): B126-B134.

[16] Wei Ji-He. Oxidation of Alloying Elements during ESR of Stainless Steel [J]. Chin J Met Sci Technol, 1989, 5:235-246.

[17] 李毅, 刘 竑, 魏季和. 不锈钢VOD精炼过程数学模拟初探 [J]. 上海金属, 2008, 30(6): 33-39.

[18] 李毅. 顶底复吹条件下不锈钢VOD精炼过程的数学模拟 [D]. 上海：上海大学,2008.

[19] 姚锡仁, 张孟亭. 多孔喷抢的冲击面积[J]. 钢铁, 1979, 6(14): 28-34.

[20] 姚俊峰, 梅炽. 卧式转炉炉衬温度场的数值模拟[J]. 中国有色金属学报, 2000, 10(4): 546-550.

[21] Oeters F. Metallurgy of Steelmaking [M]. Dösseldorf, Germany, Verlag Stahleisen mbH, 1994.

[22] Tohge T, Fujita Y, Watanabe T. Some Considerations on High Blow Rate AOD Practice with Top Blowing System [C]. Proc 4th Process Technol Conf，Iron & Steel Society, Chicago, IL, 1984: 129-136.

[23] 魏季和, 李 毅. 顶底复吹条件下不锈钢VOD精炼过程的数学模拟: 模型的应用及结果[C]. 冶金反应工程学分会，第17届全国冶金反应工程学学术会议论文集，太原, 2013.

(编辑：庞富祥)

MathematicalModelingofVODRefiningProcessofStainlessSteelunderConditionsofCombinedTopandBottomBlowing——MathematicalModeloftheProcess

WEIJihe,LIYi

(DepartmentofMaterialsEngineering,CollegeofMaterialsScienceandEngineering,ShanghaiUniversity,Shanghai200072,China)

A mathematical model for the whole VOD refining process of stainless steel under the conditons of combined top and bottom blowing was proposed and developed. The model is based on the assumptions that one part of the oxygen blown through a top lance at reduced pressure reacts with CO escaped from the bath, another part of the oxygen oxidizes the elements in the molten steel droplets splashed by the jet, and the remaining penetrates and dissolves into the molten steel through the cavity impacted by the jet. The oxygen entering into the bath oxidizes C, Cr, Si, Mn in the steel and Fe as a matrix, but the FeO formed is an intermediate product. In the combined blowing process, all the possible oxidation-reduction reactions take place simultaneously and reach their combined equilibria separately in competition at the liquid/slag and liquid/bubble interfaces. In the Ar stirring period after the top blowing operation is over, the possible reactions occur simultaneously and reach a combined equilibrium in competition at the liquid/bubble interfaces. The overall decarburization rate in the refining process is the sum of the contributions of both the top and bottom blowing processes. At higher carbon contents, the oxidation rates of elements are mainly related to the supplied oxygen rate, and at low carbon concentrations, the rate of decarburization is primarily dependent on the mass transfer of carbon in the molten steel. The un-reacted oxygen blown into the bath does not dissolve and accumulate in the steel but escapes from the bath and takes part in the post-combustion of CO in the exshuat gas. The heat transfer of the vessel was treated in terms of the two-dimensional transient heat-conduction probelms of composite multilayer walls,taking into account the influence of the operationl factors, the non-isothermal conditions and others.

stainless steel; VOD refining; combined top and bottom blowing process; mathematical modeling

2013-05-26

国家自然科学基金和宝山钢铁公司联合资助项目 (50374074)

魏季和(1942-), 男，江苏无锡人，教授,博士生导师,主要从事冶金反应工程、钢铁冶金及其物理化学、特种冶炼及 二次精炼等的研究， (E-mail)jihew@staff.shu.edu.cn

1007-9432(2014)01-0001-09

TF72

:A