一道2013年全国初中数学竞赛题的再研究

●

(秦都中学 陕西咸阳 712000)

题目如图1，已知在四边形ABCD中，AB=DC，E,F分别为AD与BC的中点，联结EF与BA的延长线相交于点N，与CD的延长线相交于点M，求证：∠BNF=∠CMF.

(2013年全国初中数学联赛初二组初赛试题)

文献[1]中作者从不同角度给出了该试题的8种证法及推广，笔者受益匪浅，启发很大.由于本试题中E,F分别是AD和BC的中点及AB=DC的特殊性，才能获得∠BNF=∠CMF.如果E,F的位置不再特殊，当AB≠DC时，∠BNF与∠CMF的关系又会怎样？∠BNF与∠CMF能相等吗？为此笔者对此题作了进一步探究，给出了此题的3种变式.

变式1将原题中条件“E,F分别为AD,BC的中点”变为“AE=λED，BF=λFC”，其他条件不变，∠BNF与∠CMF的关系如何？

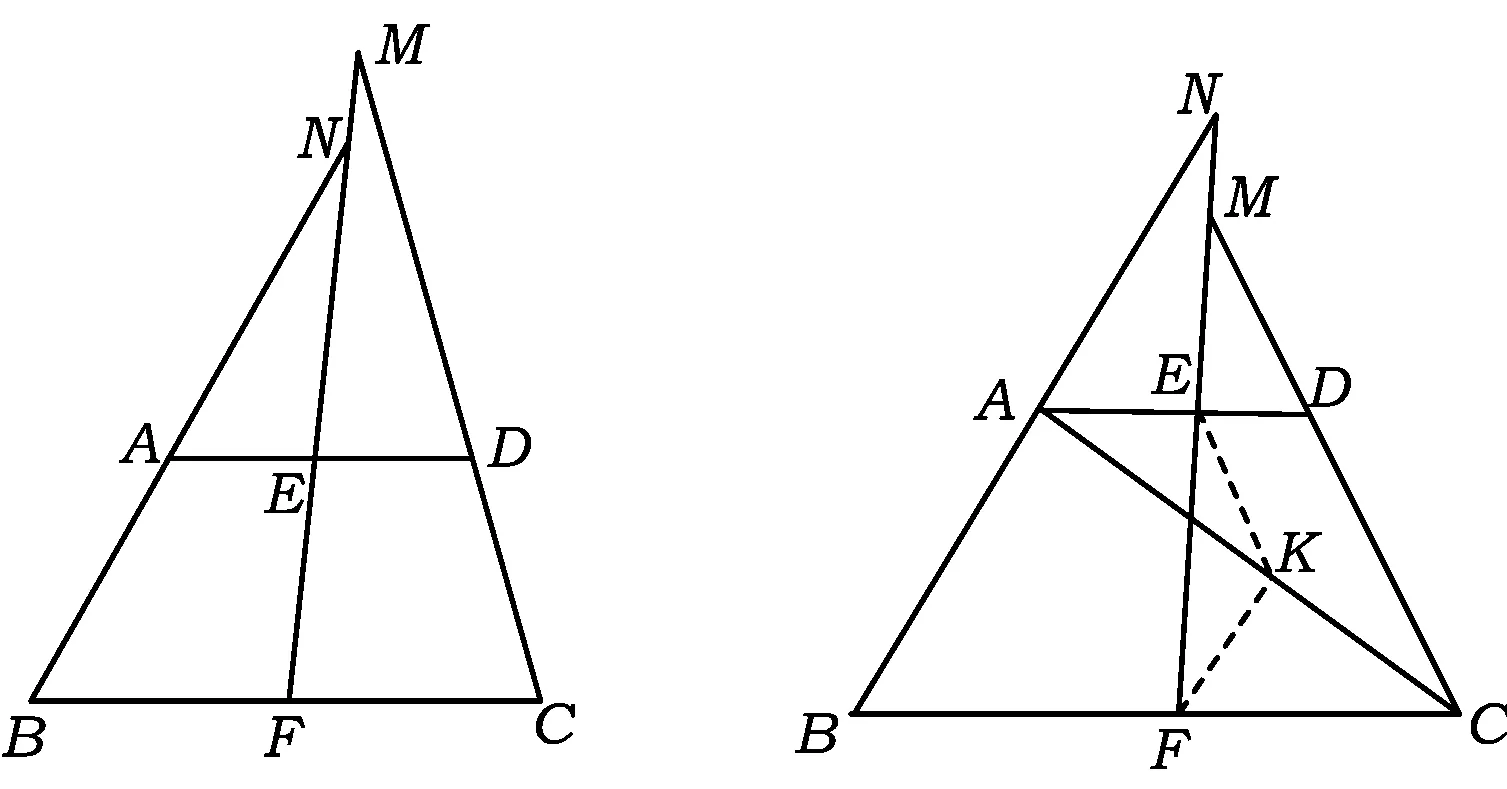
图1 图2

定理1已知四边形ABCD中，AB=DC，E,F分别为边AD和BC上的点，满足AE=λED，BF=λFC，联结EF与BA延长线相交于点N，与CD延长线相交于点M，则sin∠BNF=λsin∠CMF.

分析由于∠BNF和∠CMF及AB和DC都不在同一个三角形中，考虑到AE∶ED=BF∶FC=λ∶1,因此可过点E作EK∥DC交AC于点K，联结KF，将分散的条件集中在△EFK中，利用正弦定理证之.

证明如图2，过点E作EK∥DC，联结FK,因为

从而

KF∥AB,

所以

∠CMF=∠KEF，∠BNF=∠KFE.

在△EFK中，由正弦定理得

即

从而

sin∠KFE=λsin∠KEF,

故

sin∠BNF=λsin∠CMF.

推论1(1)当λ>1时，∠BNF>∠CMF；(2)当λ=1时，∠BNF=∠CMF；(3)当λ<1时，∠BNF<∠CMF.

变式2若条件“AB=DC”变为“AB=λDC”，其他条件不变，这时∠BNF与∠CMF的关系怎样呢？

定理2已知在四边形ABCD中，AB=λDC，E,F分别为AD，BC的中点，则sin∠CMF=λsin∠BNF.

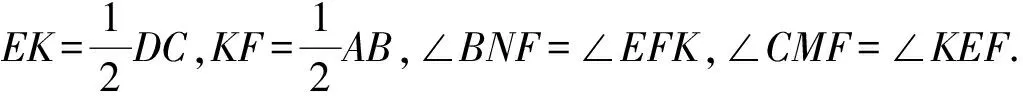
推论2(1)当λ>1时，∠CMF>∠BNF；(2)当λ=1时，∠CMF=∠BNF；(3)当λ<1时，∠CMF<∠BNF.

证明此处略.

变式3若条件“AB=DC”变为“AB=μDC”，“E,F分别为AD，BC的中点”变为“AE=λED，BF=λFC”，这时∠BNF与∠CMF的有何关系？

定理3已知在四边形ABCD中，AB=DC，E,F

分别为AD和BC边上的点，满足AE=λED，BF=λFC，则

μsin∠CMF=λsin∠BNF.

分析过点E作EK∥DC交AC于点K，联结KF，只要证明KF∥AB即可.将∠BNF,∠CMF及AB,DC集中在△EFK中，由正弦定理可证之.

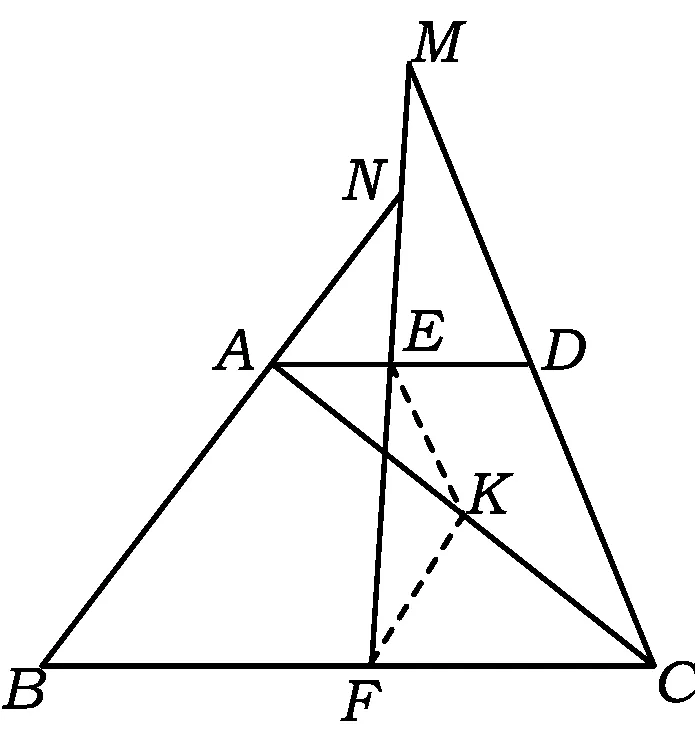
图3

证明如图3，过点E作EK∥DC交AC于点K，联结KF.由EK∥DC,得

又

从而

于是

KF∥AB.

又因为

AE=λED，BF=λFC,

所以

在△EFK中，由正弦定理得

即

故

μsin∠CMF=sin∠BNF.

推论3(1)当μ=λ时，∠CMF=∠BNF；(2)当μ>λ时，∠CMF>∠BNF；(3)当μ<λ时，∠CMF<∠BNF.

在定理3中，若μ=1，即为定理1；若λ=1，即为定理2.可见定理3是定理1和定理2的推广.

参 考 文 献

[1] 章礼抗.对一道2013年全国初中数学竞赛题的剖析[J].中学教研(数学),2013(10)：43-45.