电网主设备经济退役点研究
谢宁,王承民,肖定垚,宋枭楠
(上海交通大学,上海市200240)
电网主设备经济退役点研究
谢宁,王承民,肖定垚,宋枭楠
(上海交通大学,上海市200240)
提出了一种能定量确定电网主设备经济退役点的方法。首先假设设备的累计失效概率符合三参数威布尔分布,构建设备失效模型;其次通过最小二乘法和最大相关系数优化法确定分布参数,由此得到设备的失效率;最后假设运维成本与失效率成正比,在时间-成本坐标系上同时画出运维成本曲线和退役成本曲线,其交点即为设备最佳退役时间。最后以SF6断路器为例,描述了如何使用该方法确定电网主设备的经济退役点。
设备退役;失效率;威布尔分布
0 引 言
电力企业是设备密集型企业,实物资产占总资产的80%~90%,因此主设备的运行绩效直接影响到企业的整体效益。国外先进经验表明,基于设备的全寿命周期成本(life cycle costs,LCC)对采购、运行、检修维护及退役报废的全过程进行科学管理能够提高电力企业的综合效益。LCC是设备在预期的寿命周期内其论证、研制、生产、使用与保障以及退役处置所消耗的所有费用折现后的货币成本[1-2],即设备在整个寿命期内发生的总费用,因此取决于设备的运行年限,而后者则取决于设备的退役时间,所以确定设备经济退役点是电力企业能否进行科学合理的全寿命周期管理活动的关键。
在进行电网主设备全寿命周期管理时,需要在设备尚未入网时即确定其采购策略、运维策略和退役策略。迄今为止,该领域的研究工作大多集中于对前两者[3-6]以及LCC成本计算方法[7-10]的讨论上,而对如何制定退役策略,尤其是确定设备的经济退役点的研究十分有限。由于缺乏对资产退役标准的科学界定,主设备何时退役一直停留在定性分析的层面,在现场则多以设备的设计寿命、使用寿命参考值、在运年限等经验性判断为依据,而没有利用设备在全寿命周期内的状态评估结果来综合判定资产退役的标准和界限。例如,文献[11]认为当故障概率增加到某临界值时,设备达到其技术寿命,但该临界值是根据专家经验获得的。文献[12]以高压断路器为例,根据LCC成本分析结果确定大修和技改优选方案,但没有给出明确的经济退役时间。文献[13]在不同技改类别和运行年限条件下,对变压器技改方案进行经济评估,文中计算了变压器预运行年对应的LCC成本年金,以其最小值对应的年份作为设备经济寿命;文献[14-15]以现役变压器最大年均净收益下降到低于更换新设备的最大年均净收益作为退役标准,但是,存在成本分量多、计算复杂的缺点。
本文提出了一种确定电网主设备经济退役点的方法。在假设设备累计失效概率符合三参数威布尔分布的条件下,构建设备失效模型;其参数通过最小二乘法和最大相关系数优化法确定,由此得到设备的失效率。假设设备运维成本和失效率成正比,当运维成本与设备退役成本相等时所对应的年份即为最佳退役时间。
1 确定设备经济退役点的基本原理
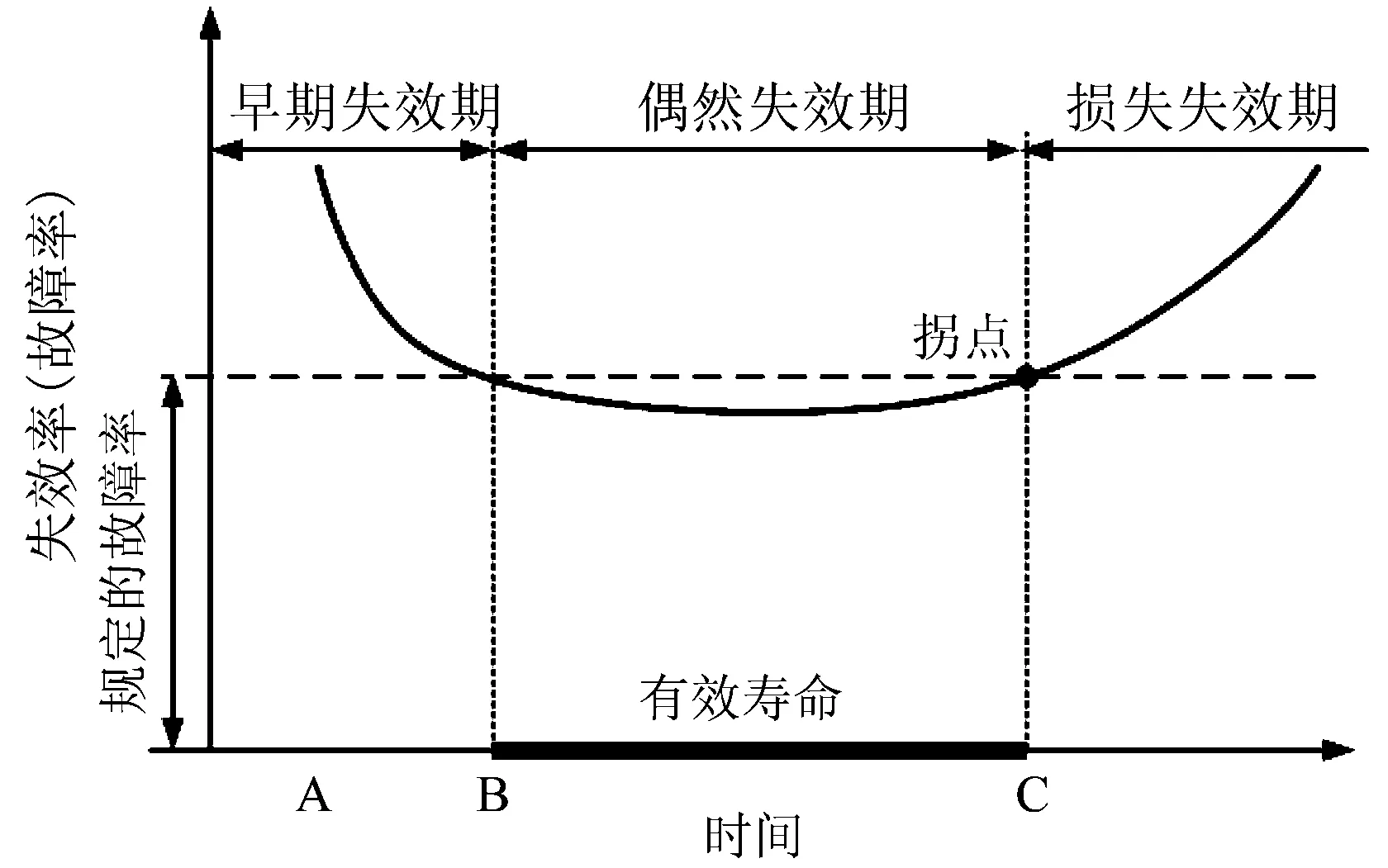
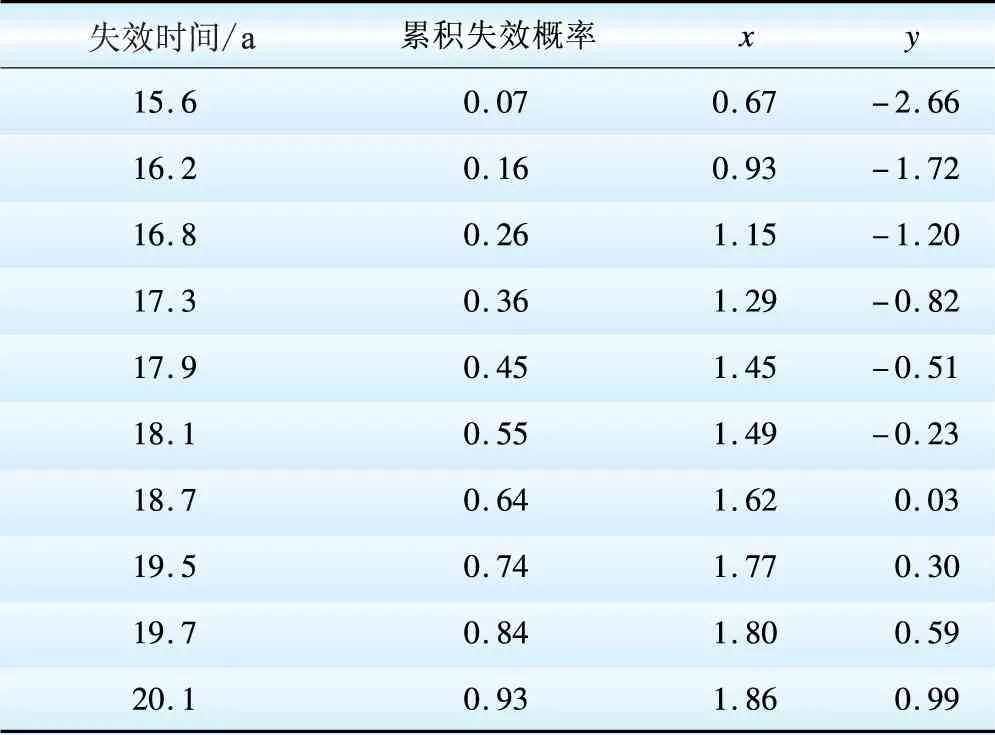
设备的退役处置成本为退役处理费减去残值。按照投资学的观点,必须对退役处置成本终值以一定的社会折现率和通货膨胀率折现,得到设备在全寿命周期内的退役处置成本现值,才能进行各种经济分析比较。显然,折现后的退役处置成本CD(t)随时间增加呈现非线性递减的规律。与之对比,设备的运行成本、维护成本、故障成本等(统称为运维成本CS(t))则随着时间增加因设备逐渐陈旧、性能变差而逐渐增加。显然,当CD(t) 在退役处置成本中,退役处理费包括进行退役处置时的人工、设备费用以及运输费,退役处理费不随时间改变,而残值体现了设备在计算期末的剩余价值,是时间的函数。若采用余额递减法,折旧率δ固定不变,且有: (1) 式中:n为估计使用年限;CI为设备初期投资费用;E(CR)为预计残值。则第t年的残值可用第t -1年的残值计算如下: CR(t)=CR(t -1)(1-δ) (2) 退役处置成本为退役处理费和残值(负值)之和。为了符合设备真实运行情况,运维成本CS(t)计算如下: CS(t)=CIλ(t) (3) 式中:CI为设备初期投资费用;λ(t)为失效率,由第3节所述方法确定。当退役处置成本和运维成本相等时所对应的点即为最佳退役点。 2.1 基于三参数威布尔分布的失效模型 设备累计失效概率F(t)指设备在规定的条件和时间内发生故障的概率,也称为不可靠度,在失效模型中,就是寿命分布函数。 F(t)=1-R(t) (4) 式中:R(t)为设备的可靠度函数。 历史经验表明,在电力设备的寿命分布类型中,指数分布、威布尔(Weibull)分布、正态分布比例占80%以上,而指数分布和正态分布是威布尔分布的特例;另外,威布尔分布应用比较广泛,对各种类型的试验数据的适应能力较强[15],所以不失一般性,本文假定电网主设备的寿命分布符合威布尔分布规律。一个符合三参数威布尔分布的累计失效概率函数为 (5) 式中:m为形状参数,m>0;η为尺度参数,反映了设备的特征寿命,η>0;γ为位置参数,也称最小寿命,表示设备在γ以前不会失效,γ≥0,当γ=0时退化为两参数威布尔分布;t为设备的工作时间,t≥γ。 电网设备在全寿命周期内的失效率(故障率)是工作到t时刻尚未失效的设备在该时刻后的单位时间内发生失效的概率,定义为 (6) 失效率分布规律呈浴盆形状,称为浴盆曲线,如图 1所示,分为早期失效期、偶发失效期和耗损失效期3个阶段。浴盆曲线可以很好地用威布尔分布来拟合,3个阶段分别对应形状参数0 符合三参数威布尔分布的失效率表示为 (7) 通过分析同一类型电气设备历史统计数据,可以对基于威布尔分布的失效率曲线进行分段拟合,求得浴盆曲线各阶段的形状参数m,尺度参数η,以及位置参数γ。 图1 设备失效率浴盆曲线 2.2 模型参数估计 估计模型参数时,首先要对样本数据进行预处理,即对设备寿命试验数据进行筛选,取10~20个设计/制造相同、运行环境相似的设备作为一个样本组,寿命统计区间以3~5年为一段。如此处理,有助于突出在寿命的不同阶段失效率变化的特点。 假设一共有N个设备的寿命试验数据,失效时间顺序为t1≤t2≤…≤tN,对应F(t1)≤F(t2)≤…≤F(tN),则其中第i个设备失效时对应的累计失效概率可利用中位秩法近似求得: (8) 假设位置参数γ已知,则可以利用最小二乘法回归求出形状参数m和尺度参数η,然后利用最大相关系数优化法估算位置参数。 对式(5)两侧同取2次自然对数得 (9) 令 (10) 则式(9)被转换为线性方程 y=mx-B (11) 利用最小二乘法,有 (12) (13) 式中N为设备寿命试验数据总数。 显然,尺度参数 (14) 下面估算位置参数,式(10)中x和y之间的相关系数定义为 (15) 该系数体现了设备寿命服从威布尔分布的程度,显然0 < |R(x,y)|≤1;其值越接近于1,说明服从程度越好,也就是说满足以下条件的位置参数γ即为所求 (16) 经过数学推导,可知γ应满足: (17) 若为两参数威布尔分布,γ退化为0,无须确定;参数m和B仍由式(12)求出;尺度参数由式(14)求出;拟合效果由相关系数式(15)进行检验,|R(x,y)|值越接近1,说明拟合程度越高。 估算出所有参数后,按式(7)求出失效率,再按式(3)计算即可得到设备的运维成本。 本节以SF6断路器为例,说明如何利用所述方法确定设备的经济退役点。选取10 台SF6断路器进行可靠性试验,失效时间列于表 1的第1列。假设失效率服从威布尔分布,样本数据中第i个设备对应的累计失效概率F(ti)按式(8)近似计算(本例中N=10),对应的累计失效概率列于表 1的第2列。xi和yi按式(10)计算,结果列于表 1的第3、4列。 表1算例分析计算结果 Tab.1Calculationresultsofexampleanalysis 假设位置参数γ已知,其初值可选择接近且小于第1个失效时间(15.6年)的值,本例中取γ的初值为13。利用最小二乘法进行回归,求出形状参数m=2.81、尺度参数η=4.47。 下面根据第3节所述最大相关系数优化法来计算位置参数γ。公式(15)对γ一阶求导,令导数为0,得到γ≈ 13.65,因此与所选样本组设计/制造相同、运行环境相似的SF6断路器失效率模型为 (18) 设备最佳退役时间的确定是假设设备运维成本与失效率函数成正比,比例系数为设备初期投资费用。本案例中SF6断路器的投资成本为2.7万元,与上述失效率的乘积得到运维成本曲线如图 2中实线所示,随时间增加呈现非线性递增的规律。 假设SF6断路器预计使用年限为20年,设备原值为2.7万元,预计残值取原值的5%。利用式(1)计算出SF6断路器的折旧率δ=0.139,然后由式(2)得到设备在各年度的残值。该型断路器退役处置费用为1.1万元,与残值(负值)之和即为退役处置成本,如图 2中虚线所示,随时间增加也呈非线性递增的规律,但增加幅度小于运维成本的幅度。在17.3年左右两成本相等,过了这个点,设备的运维成本将高于退役处置成本,所以该点是符合该样本组累计失效概率分布的SF6断路器的最佳退役时间。 图2 确定设备经济退役时间示意图 本文提供了一种基于三参数威布尔分布确定电网设备最佳退役时间的方法,为制定资产全寿命周期管理策略,尤其是运维策略和退役策略,提供科学依据。该方法的主要优点包括:(1)普适性。历史经验表明,电网设备的寿命分布类型中指数分布、威布尔分布、正态分布比例占80%以上,而指数分布和正态分布是威布尔分布的特例,所以以威布尔分布作为电网设备的寿命分布类型具有普适。(2)精度高。相对于二参数威布尔分布而言,三参数威布尔分布对于各种类型的实验数据拟合能力更强,尤其是对那些以损耗失效为特征的电网设备拟合精度更高,更能反映设备失效的实际情况。(3)计算量小。利用最小二乘法和最大相关系数优化法确定威布尔分布系数,计算量小,且能保证一定的精度。 该方法符合全寿命周期管理体系的发展需要,可纳入企业制定实现综合绩效最优的管理策略框架内,具有非常广阔的应用前景。 [1]International electrotechnical commission.IEC 60300-3-3 Second Edition, Dependability management-part 3-3 :Application guide-life cycle costing[S]. Switzerland: IEC,2004 [2]PaulBarringer H. Life Cycle Cost And Good Praetiee[C]//NPRA Maintenanee Conferenee, 1998. [3]殷可,郁东升,李莉华,等.500 kV变压器招标采购中 LCC 方法的应用研究[J].华东电力,2009,37(5): 741-744. [4]滕乐天,陈红兵,王怡风.LCC 在设备采购中的应用实践[J]. 华东电力,2007,35(10): 27-29. [5]章健,张弛,蒋声婴,等.基于LCC的配电站设备检修策略研究[J].华东电力,2012,40(09):1576-1579. [6]朱承治.输变电设备优化检修(OM)若干关键技术研究[D].杭州:浙江大学,2008. [7]Jeromin I, Balzer G, Backes J, et al. Life cycle cost analysis of transmission and distribution systems[C]//PowerTech, 2009 IEEE Bucharest, IEEE, 2009: 1-6. [8]上海市电力公司.一种电力系统LCC控制方法[P].中国专利:CN101446985,2009.6.3. [9]王建.全寿命周期成本理论在电力系统投资决策中的应用研究[D].重庆:重庆大学,2008. [10]周涛.基于全寿命周期的电网主设备成本分析与应用研究[D].北京:华北电力大学,2012. [11]黄炜昭,皇甫学真,陈建福,等.电网主设备运行维护策略辅助决策方法[J].电力系统自动化,2013,37(10):119-123. [12]杜永平,李泓泽,赵宏,等.高压断路器大修与技改项目的优选[J].安徽电气工程职业技术学院学报,2010,15(001): 1-7. [13]郝洵.基于全寿命周期成本的变压器技改评估[D].武汉:华中科技大学,2011. [14]刘有为,马麟,吴立远,等.电力变压器经济失效模型及应用实例[J].电网技术, 2012,36(10):240-245. [15]张晨.基于可靠性的设备经济寿命与预防性维修周期的研究[D].南京: 南京理工大学,2006. (编辑:张小飞) EconomicDisposalTimeofPrimaryElectricityEquipments XIE Ning, WANG Chengmin, XIAO Dingyao, SONG Xiaonan (Shanghai Jiaotong University, Shanghai 200240, China) This paper proposed an approach for the quantitative determination of economic disposal time of primary electricity equipments. Firstly, the failure mode of equipments was constructed under the assumption that the accumulated failure probability could be described by three-parameter Weibull distribution. Secondly, the distribution parameters were determined by the least square method and the maximum correlation coefficient optimization method, so as to obtain the failure rate of equipments. Thirdly, with assuming that the operation-maintenance cost was proportional to the failure rate, the economic disposal time of the equipments was the intersection of the disposal cost curve and the operation-maintenance cost curve in the same time-cost coordinate system. Finally, taking SF6circuit breaker as example, this paper described how to use this method to determine the economic disposal time of primary electricity equipments. equipment disposal; failure rate; Weibull distribution F 407.61 : A : 1000-7229(2014)06-0165-04 10.3969/j.issn.1000-7229.2014.06.031 2013-12-09 :2014-01-10 谢宁(1973),女,博士,副教授,主要从事电力系统安全稳定分析、电力系统经济运行、智能电网的研究工作,E-mail:xiening@sjtu.edu.cn; 王承民(1970),男,博士,副教授,主要从事电力系统安全稳定分析、电力系统经济运行、电力市场的研究工作,E-mail:wangchengmin@sjtu.edu.cn; 肖定垚(1990),男,硕士研究生,主要从事电力系统安全稳定分析、电力系统经济运行、电力市场的研究工作,E-mail:276259574@qq.com; 宋枭楠(1990),男,硕士研究生,主要从事电力系统安全稳定分析、电力系统经济运行、电力市场的研究工作,E-mail:song8922009@163.com。2 设备失效模型
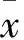

3 算例分析

4 结 语

