风力发电系统液压变桨执行机构的H∞控制

陈金元，李相俊，谢巍

(1.华南理工大学自动化科学与工程学院，广州市510641；2.中国电力科学研究院电工与新材料研究所，北京市100192)

风力发电系统液压变桨执行机构的H∞控制

陈金元1，李相俊2，谢巍1

(1.华南理工大学自动化科学与工程学院，广州市510641；2.中国电力科学研究院电工与新材料研究所，北京市100192)

风力发电中风速的波动将会引起输出功率的波动，基于变桨执行机构快速地跟踪桨距角命令，变桨恒功率控制可平抑输出功率的波动。液压变桨执行机构以其响应频率快、扭矩大、便于集中布置和集成化等优点在目前的变桨距执行机构中广泛应用。常规比例积分(proportional integral, PI)控制的液压变桨执行机构，具备一定的动态响应性能，但其鲁棒稳定性相对不好。为此，针对液压变桨执行机构设计了H∞控制器，不仅能快速有效地跟踪桨距角命令，还能在变桨执行机构存在参数不确定性情况下，保持系统稳定，同时具备优良动态性能，鲁棒性好。仿真分析表明：相比PI控制，H∞控制系统各方面性能较优越。在设计H∞控制器过程中，提出了一种新的加权函数的快速构造方法。研究结果表明：提出的方法能快速地构造所需的加权函数，为H∞控制在工业上的应用提供参考。

风力发电；液压变桨执行机构；H∞控制器；构造方法；加权函数

0 引 言

化石燃料的枯竭问题以及使用这些化石燃料带来的环境问题日益受关注，充分利用可再生的、清洁的风能成为解决这些问题的有效办法。然而，风速的波动将会引起输出功率的波动，给电网带来不利影响[1]。为了平抑这种功率波动，研究人员提出了定桨失速[2]、变桨恒功率[3-4]、变桨变功率[5]、储能平滑[6-7]等控制方法。变桨恒功率控制是在额定风速之上切出风速以下时，改变风机叶片的桨距角，使得风机输出功率保持恒定。

为了达到变桨恒功率的目的，就要求变桨执行机构能够快速地跟踪桨距角命令。液压变桨执行机构以其响应频率快、扭矩大、便于集中布置和集成化等优点在目前的变桨距执行机构中广泛应用。液压变桨执行机构的常规控制策略为比例积分(Proportional Integral, PI)控制，然而PI控制快速性、鲁棒性、抑制干扰方面控制效果不理想，故提出了更先进的鲁棒H∞控制。在设计H∞控制器过程中，加权函数的构造至关重要。文献[8-10]仅仅指出了加权函数应满足的约束条件，未具体指出构造方法，设计的控制器阶次高，无法快速构造加权函数。文献[11]提出了基于约束目标免疫算法的构造方法，但这种方法算法复杂度高，构造时间长，难以推广应用。本文提出一种快速构造加权函数的方法，不仅能快速地构造需要的加权函数，且设计出的控制器阶次低。

1 液压变桨执行机构

1.1 变桨恒功率原理

定桨距风力发电又称作失速型风力发电，其叶片与轮毂的连接是固定的。当风速变化时，叶片的迎风角度不随之变化，即叶片桨距角不能调节。当风速高于额定风速时，叶片必须能够自动地将功率限制在额定点附近，而不能超过风力发电机材料的物理性能使用限度，叶片的这一特性称为自动失速性。其缺点是风电机组的性能受叶片失速性能的限制，启动风速较高，在风速超过额定值时发电功率有所下降，同时需要叶尖刹车装置[12]。

变桨距风力发电机组中，叶片的桨距角可以自动进行调节。在额定风速与切出风速之间，采用变桨的方式使发电系统输出恒定的功率。其变桨恒功率原理可用式(1)来阐述，通过改变桨距角β的大小，改变风能利用系数Cp的值，进而改变输出功率Pω的大小。

(1)

式中：λ=ωωR/Vω，为叶尖速比；ωω为风轮角速度；Vω为风速；R为风轮半径；ρ为空气密度,Γ为中间变量[13-14]。

变桨距调节的优点是机组启动性能好，输出功率稳定，机组结构受力小，停机方便安全；变桨距调节提供了较好的输出功率品质，并且每一叶片调节器的独立调桨技术可看作是一个独立的制动系统，并可以独立调节。显然，变桨距风力发电机更具发展优势。

1.2 液压变桨执行机构及其传递函数模型

根据控制方式的不同，变桨执行机构分为2类，一类是电动变桨执行机构，一类是液压变桨执行机构。

电动变桨距执行机构利用电动机对桨叶进行单独控制，由于其机构紧凑可靠，比液压变桨距传动结构相对简单，不存在泄漏、卡涩等问题，所以也得到许多生产厂家的青睐。但其动态特性相对较差，有较大的惯性，特别是对于大功率风力机。而且电机本身如果连续频繁地调节桨叶，将产生过量的热负荷使电机损坏。关于此产品，国外比较具有代表性的公司有Nordex、Suzlon和GEWindEnergy公司等[15]。

液压变桨执行机构通过液压系统推动桨叶转动，改变桨距角。该机构以其响应频率快、扭矩大、便于集中布置和集成化等优点在目前的变桨距机构中广泛应用。国外著名的风力机厂丹麦的Vestas，德国的Dewind、RePower等都采用液压变桨距方式。

液压变桨执行机构的机械图及工作过程可参见文献[3]。变桨执行机构根据桨距角命令，并监控叶片角度反馈来调整叶片角度的最佳位置。变桨执行机构控制系统框图如图1所示，其中βcmd、β分别为桨距角命令值、桨距角输出值，τ为时间常数。βcmd为基于变桨恒功率原理，根据风速变化给定的量。无控制器作用时，变桨执行机构实际等效于一阶惯性环节，其传递函数为：

(2)

式(2)中τ=10。

图1 变桨执行机构

2 鲁棒H∞混合灵敏度控制

2.1 标准鲁棒H∞混合灵敏度控制

图2为标准鲁棒H∞混合灵敏度控制系统框图。图中：K为H∞控制器；G为控制对象；r、d分别为给定输入和干扰输入，统称为外部输入w；u、y、z分别为控制量、输出、性能评价信号；W1、W2、W3为加权函数[16-18]。

从w到z的闭环传递函数矩阵Tzw(s)可表示为

(3)

式中：S为灵敏度函数，S=1/(1+GK)；R=KS；T为补灵敏度函数，T=GK/(1+GK)。

H∞控制器设计问题为寻找真实有理函数控制器的K，使闭环系统稳定，并且使传递函数阵Tzw(s)的H∞范数极小化即

(4)

将式(4)转化为

(5)

图2 标准鲁棒H∞混合灵敏度控制系统框图

2.2 加权函数设计

在鲁棒H∞混合灵敏度问题中，要求设计加权函数W1、W2、W3使系统有较好的性能。W1是对灵敏度函数S的加权，S是干扰输入d到系统输出y的传递函数，同时也是参考输入r到跟踪误差e的传递函数；W2为控制变量u的加权；W3是对补灵敏度函数T的加权，表示乘性摄动的范数界，反应了鲁棒稳定性要求及高频特性要求[13-15]。

基于频域整形原理，提出了鲁棒H∞混合灵敏度加权函数的新设计方法，包括下列步骤：

(1)构造加权函数W1、W2、W3如下

(6)

式中：K1为被控系统期望的低频增益；K2为W3的放大系数；K3为W3的放大系数；A为W3的剪切频率与ωc的位置关系参数；ωc为被控系统期望的剪切频率。K1、K2、K3和ωc需要同时满足下述约束条件：

(7)

式中：umax为控制量u的上限值；ωd为被控系统中干扰信号的频率上限。

需要说明以下几点：

1)图3是构造W1、W3的频域整形原理图。L为期望系统的开环传递函数，阴影部分表示L的可能取值区域。频域整形原理可表示为

S=I/(I+L)≈L-1

(8)

T=L/(I+L)≈L

(9)

加权函数须满足

(10)

图3 频域整形原理

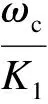
(2)通过Matlab的augtf与hinf函数，利用G、W1、W2、W3即可计算出H∞控制器；若H∞控制器无解或期望加入控制器后的系统具有更佳的动态品质和稳态性能，则返回至步骤(1)重新对K1、K2、K3、A和ωc进行设置。

通过以上方法，设计的控制器阶次将比控制对象的阶次仅多1次，降低了控制器的复杂性、难实现性。

2.3 液压变桨执行机构H∞控制器设计

在液压变桨执行机构中，其广义被控对象为Gopn。作Gopn的bode图如图4所示，其截至频率为0.1 rad/s，故期望截止频率ωc可设为8.13 rad/s。变桨执行机构无干扰、控制量无具体要求，故取满足约束条件的K1、K2、K3、A分别为200、0.01、0.1、5，即加权函数为

(11)

得到控制器为

(12)

控制器阶次为2，阶次较低。

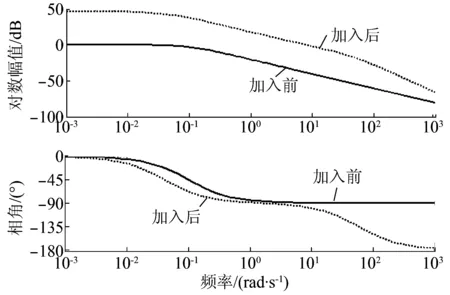
图4 加入控制器前后系统开环bode图

由图4可看出：加入H∞控制器后，系统低频部分得到改善，截止频率增大。

图5为加入H∞控制器后，系统灵敏度函数、补灵敏度函数与加权函数的关系。可见，灵敏度函数范数小于加权函数W1-1范数，补灵敏度函数范数小于加权函数W3-1范数，达到设计要求。

3 仿真与分析

本文基于Matlab/Simulink软件进行了仿真分析。输入桨距角命令为模拟的每3 s变化一次的随机信号，变化范围0～90。PI控制器设计时采用的是闭环极点配置法，配置的系统闭环极点为s1=-10，s2=-3，配置这2个闭环极点一是为使系统有足够的稳定裕度，二是为使系统无共轭复根，达到不振荡的效果。得到控制器参数为Kp=129，Ki=300，PI控制器的传递函数为

图5 灵敏度函数、补灵敏度函数与加权函数关系

(13)

仿真结果见图6、7所示。由图6可以得出：从调节过程上看，H∞控制过程平滑，无振荡过程，PI控制过程出现明显振荡，对于具有延迟特性的桨距角执行机构，振荡不仅给执行机构带来硬件上的损伤，且执行机构很难满足这种高灵敏性要求；从调节时间上看，H∞控制调节时间明显小于PI控制。从图7桨距角跟踪误差统计图可以看出，H∞控制跟踪误差集中在±1内，而PI控制跟踪误差集中在±5内，可见H∞控制跟踪性能优于PI控制。

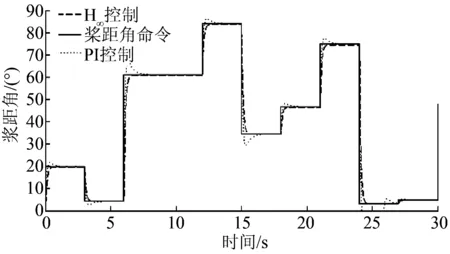
图6 跟踪桨距角命令

本文针对时间常数变动范围为0.8τ～1.2τ的情况，对鲁棒H∞控制器的控制效果作了仿真，其仿真结果见图8、9及表1。为了便于观察结果，图8为截取的时间为0～1 s时间段的桨距角跟踪命令图。可见，即使τ变动-20%～20%，鲁棒H∞控制器依然能使变桨执行机构的跟踪效果良好，其跟踪性能与τ变动前的差别不大。

图7 桨距角跟踪误差统计

在频域内对系统进行分析，鲁棒H∞控制器作用时，对变桨系统的开环传递函数作其bode图，见图9，充分体现了即使τ变动，其频率特性基本一致的特性。图9中5个圆点对应为频率特性中的截止频率所在的点，其详细数据见表1。在频域内，截止频率与相角裕度是非常重要的性能指标；5个点的截止频率与相角裕度都相差不大，更加体现其频率特性基本一致，系统非常稳定。图8、9及表1进一步说明了在鲁棒H∞控制器作用下，即使τ变动，系统的跟踪性能、稳定性都基本一致，体现本文设计的控制器具有良好的鲁棒性。

图8 τ变动时桨距角跟踪命令

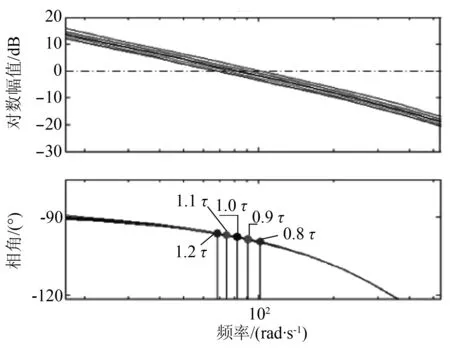
图9 τ变动时bode图

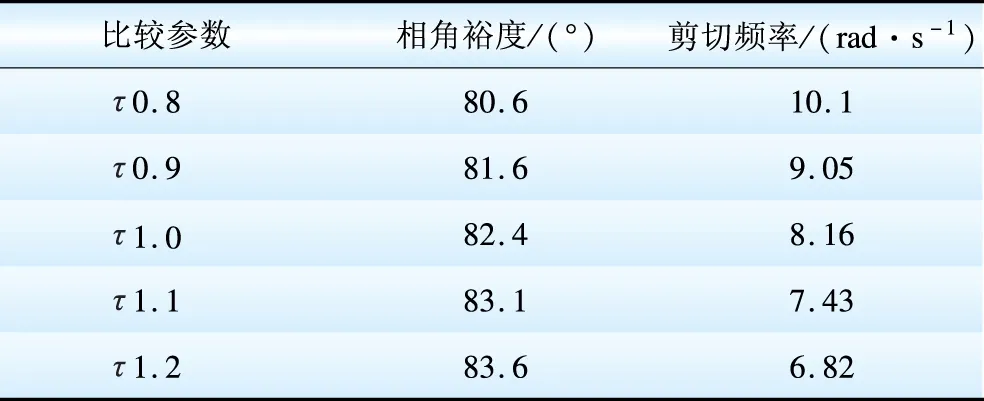
表1 τ变动时频域性能指标

4 结 论

针对风力发电系统中的液压变桨执行机构，运用鲁棒H∞混合灵敏度控制理论，设计了H∞控制器，通过仿真分析，鲁棒H∞控制能快速有效地跟踪桨距角命令，并对比PI控制系统性能，验证了H∞控制器的优越性。并且，通过改变液压变桨执行机构模型参数的变动范围，验证了具有H∞控制器的液压变桨执行机构，能在满足良好的跟踪性能的同时具备鲁棒性。在设计H∞控制器过程中，提出了一种加权函数的快速构造方法，不仅能快速地构造需要的加权函数，且设计出的控制器阶次低，为H∞控制在工业上的应用提供参考。

[1]Sheikh M R I，Muyeen S M，Takahashi R，et al.Minimization of fluctuations of output power and terminal voltage of wind generator by using STATCOM/SMES[C]//2009 IEEE Bucharest.PowerTech，IEEE，2009：1-6.

[2]陈家伟，龚春英，陈杰，等.中小型风力发电机组恒功率软失速控制策略[J].电工技术学报，2013，28(1)：149-156.

[3]林勇刚.大型风力机变桨距控制技术研究[D].杭州：浙江大学，2005.

[4]Maureen H M.Systematic control design methodology for variable-speed wind turbin[R]. Colorado USA： National Renewable Energy Laboratory，2002.

[5]Li X J, Hui D, Lai X K，et al.Control strategy of wind power output by pitch angle control using fuzzy logic[C]//2010 IEEE International Symposium on.Industrial Electronics(ISIE),IEEE，2010：120-124.

[6]Li X J, Hui D, Lai X K.Battery energy storage station(bess)-based smoothing control of photovoltaic(pv)and wind power generation fluctuations[J].IEEE Transactions on Sustainable Energy，2013，4(2)：464-473.

[7]张步涵，曾杰，毛承雄，等.电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术，2006，30(15)：54-58.

[8]吴旭东，解学书.H∞鲁棒控制中的加权阵选择[J].清华大学学报：自然科学版，1997，37(1)：27-30.

[9]黄曼磊. 鲁棒控制理论与应用[M].哈尔滨：哈尔滨工业大学出版社，2007：55-61.

[10]樊树军.H∞混合灵敏度设计问题仿真研究[D].哈尔滨：哈尔滨工业大学，2010.

[11]王杰，王栓，朱晓东，等.基于约束多目标免疫算法的H∞混合灵敏度加权阵选择[J].电力自动化设备，2009，29(1)：37-40.

[12]顾鑫.兆瓦级风力发电机组液压变桨距系统研究[D].无锡：江南大学，2008.

[13]刘玮.风力发电机组液压变桨距系统的建模以及故障诊断[D].北京：华北电力大学，2009.

[14]赵永祥.变速恒频双馈风力发电系统转速控制[D].天津：天津大学，2007.

[15]杨俊华.无刷双馈风力发电系统及其控制研究[D].广东：华南理工大学，2006.

[16]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京：清华大学出版社，2002:41-43.

[17]申铁龙.H∞控制理论及应用[M].北京：清华大学出版社，1996:67-70.

[18]冯纯伯，田玉平，忻欣.鲁棒控制系统设计[M].南京：东南大学出版社，1995:53-56.

(编辑：蒋毅恒)

H∞ControlofHydraulicVariablePitchActuatorinWindPowerGenerationSystem

CHEN Jinyuan1, LI Xiangjun2, XIE Wei1

(1. School of Automation Science and Engineering, South China University of Technology, Guangzhou 510641, China;2.Electrical Engineering and New Material Department, China Electric Power Research Institute, Beijing 100192, China)

Variable wind can cause output power fluctuation in wind power system; however the constant power control with variable pitch can stabilize the output power fluctuation based on that the variable pitch actuator can quickly and efficiently track pitch angle command. Due to the advantages of fast frequency response, big torque, easily focus layout and integration, the hydraulic variable pitch actuator was widely applied. With the conventional PI (Proportional Integral)control, the hydraulic variable pitch actuator had a certain dynamic response performance, but its robust stability was relatively bad. Thus, the H∞controller for the pitch variable pitch actuator was designed, which could quickly and efficiently track pitch angle command, keep system stable under the condition that the parameters of hydraulic variable pitch actuator were uncertain, and have good dynamic performance and robustness. The simulation results show that the performances of H∞control system are superior compared that of PI control. In the design process of H∞controller, a new fast construction method of weighting function was proposed. The research results show that the proposed method can quickly construct needed weighting functions, and provide references for the application of H∞control in industry.

wind power; hydraulic variable pitch actuator; H∞controller; construction method; weighting function

国家自然科学基金项目(51107126)；广东省自然科学基金面上项目(S2013010012537)；河北省重大科技成果转化专项(13044407Z)。

TM 73

： A

： 1000-7229(2014)06-0001-06

10.3969/j.issn.1000-7229.2014.06.001

2014-02-24

：2014-03-07

陈金元(1990)，男，硕士研究生，研究方向为鲁棒控制，新能源与分布式发电，E-mail：chenjinyuan1990@163.com；

李相俊(1979)，男，工学博士，高级工程师，研究方向为电池储能系统控制、新能源与分布式发电、鲁棒控制；

谢巍(1974)，男，教授，博士生导师，研究方向为鲁棒控制。