基于改进遗传算法的光伏发电并网优化配置
包广清,杨国金,杨勇,常勇
(1.甘肃省工业过程先进控制重点实验室(兰州理工大学),兰州市 730050;2.甘肃省电力科学研究院,兰州市 730050)
基于改进遗传算法的光伏发电并网优化配置
包广清1,杨国金1,杨勇2,常勇1
(1.甘肃省工业过程先进控制重点实验室(兰州理工大学),兰州市 730050;2.甘肃省电力科学研究院,兰州市 730050)
光伏发电在未来将成为新增分布式发电系统的主流,为此研究了光伏发电并网的优化配置问题。建立了光伏电源选址和定容的配电网络损耗最小、节点电压偏移最小和接入费用最小的多目标优化模型;提出了一种改进的基于遗传算法的并列选择法;突出优化重点目标,对各目标函数区别对待,在前推回推法计算配电网潮流的基础上,采用该改进的算法求得模型的最优解;最后通过IEEE33节点算例系统对模型和算法进行了测试,结果表明所建模型的正确性和改进算法的优越性。
光伏发电;配电网;潮流计算;遗传算法;优化配置
0 引 言
分布式发电(distributed generation,DG)设备一般是集成或单独使用的、靠近用户的小型模块化发电设备,多为容量在50 MW以下的小型发电机组。分布式电源主要包括风力发电场、光伏电池、燃料电池、微型燃气轮机、地热发电装置、储能装置等[1-2]。分布式发电具有对环境污染少,降低线路损耗,改善供电质量,提高供电可靠性等优点[3],它与大电网系统相结合是电力系统的主要发展方向。但是随着分布式电源渗透率的不断提高,对配电网的稳态电压、线路潮流、短路电流等带来较大影响[4],其影响程度与接入分布式电源的位置和容量大小密切相关[5-6]。因此,合理地规划分布式电源位置和容量对发挥其优点,解决相关问题十分必要。
国内外针对分布式电源的规划问题已经开展了相关研究。文献[7]基于双母线模型,给出了并入分布式电源前后负荷节点电压的变化,并没有给出多负荷节点配电网络电压变化情况,只研究了单个分布式电源的情况。文献[8]讨论了分布式电源出力、接入位置变化对配电网节点电压的影响情况。文献[9]应用遗传算法对配电网扩展规划中分布式电源的位置和容量进行优化,但仅以费用最小为目标函数,未考虑节点电压偏移、网络损耗等因素。
光伏发电在未来将成为新增分布式发电的主流。为促进光伏发电产业的发展,国家实施了“金太阳示范工程”,2013年初又发布《关于做好分布式光伏发电并网服务工作的意见》,规定单个装机容量不超过6 MW的分布式电源可免费接入电网。为此,本文以光伏电源作为接入配电网的分布式电源,以配电网网络损耗最小,节点电压偏移最小和接入费用最小为目标函数,以分布式电源容量和位置为自变量,在前推回推法[10]计算配电网潮流基础上,基于英国设菲尔德(Sheffield)大学推出的MATLAB遗传算法工具箱[11],提出一种改进的并列选择法对多目标函数进行最优求解,以实现对光伏电源接入配电网的位置和容量的最优规划,最后利用IEEE33节点配电系统对优化结果和改进的算法进行验证[12]。
1 光伏电源选址和定容优化规划模型
1.1 光伏电源选址和定容的目标函数
目标函数1:配电网网损最小。设Ploss为系统网损,Ploss可表示为
(1)
则配电网网损最小的目标函数为
(2)
式中:ΔPLi为第i条支路有功功率损耗,kW;Cj为除i节点外所有与j节点相连的节点的集合;Pj为节点j流入的有功损耗,kW;Pjk为与j节点相连的节点k流入的有功损耗,kW;Qj为节点j流入的无功损耗,var;Qjk为与j节点相连的节点k流入的无功损耗,var;Rij为支路i、j的支路阻抗,Ω;Uj为节点j的电压, kV。
目标函数2:节点电压偏移最小。设Umax为各节点电压与额定电压偏差最大值,则Umax可以表示为
(3)
式中:Ui为节点i在接入光伏电源后的电压值, kV;UNi为节点i的额定电压值, kV。
则节点电压偏移的目标函数为
(4)
目标函数3:光伏发电接入费用最小。对于光伏发电并网,以1 MW的光伏发电项目为例,通常接入点需要10个以上,而1个光伏并网接入点的费用就是40万元。
则光伏发电接入费用最小的目标函数为
minf3=min(40m)
(5)
式中m为配电网中光伏电源的接入点个数。
1.2 约束条件
(1)系统功率平衡约束条件。
(6)
式中:PGi、QGi分别为节点i注入的有功功率和无功功率,kW和var;PDGi、QDGi分别为节点i光伏电源注入的有功功率和无功功率,kW和var;PLi、QLi分别为节点i的有功和无功负荷,kW和var;Ui、Uj分别为支路首末节点i和j的电压, kV;δij为首末节点i、j的支路的功率因数角,(°);Gij、Bij分别为对应支路的支路电导和电纳,S。
(2)支路有功功率约束条件。
PLi≤Pimax
(7)
式中:PLi为支路i有功功率,kW;Pimax为支路i允许的最大功率,kW。
(3)分布式电源运行约束。
PDGi≤PDGi,max
(8)
式中:PDGi,max为单个DG接入配电网的最大限制功率,kW;PDGi为i点的DG接入功率,kW。
2 算法的研究
遗传算法具有全局收敛能力强等优点[12],考虑到光伏电源的选址和定容的特点,本文采用一种改进的并列选择法优化光伏电源的位置和容量。
2.1 改进算法的原理
并列选择法的思想是:先将群体中的全部个体按子目标函数的数目均等(m/n)地划分给各子群体,对每个子群体分别进行选择运算得到新个体;然后将这些新个体合并成为一个完整的群体;再对其进行交叉和变异运算;这样不断地重复操作,最终求出多目标优化问题的多目标最优解。很显然,这种均等划分群体的方法,没有区分各目标函数主次。实际中,进行多目标优化时,在综合考虑各目标函数的同时,往往更看重某个或某几个目标函数,所以改进的并列选择法在给各个子目标函数分配子群体时并不进行均等划分,而是给最关注的目标函数分配以较多的个体,以使其有更大的搜索空间,进而在不影响其他子目标函数寻优结果的前提下,能够准确、迅速地找到妥协于最关注目标函数的最优解,交叉与变异运算不变。图1为改进的并列选择法的示意图。

图1 改进的并列选择法
2.2 多目标寻优的流程
(1)编码。采用二进制编,染色体长度为33,基因位元素为1和0。
(2)选择算子。采用的选择(复制)算子使用随机遍历抽样法按照个体在当前种群中的适应度为繁殖概率选择父代。
(3)交叉算子。采用单点交叉法,对个体进行两两随机配对,依设定的交叉概率(Pc)在交叉点处相互交换2个个体的部分染色体,从而产生2个新个体,本文取Pc=0.99。
(4)变异算子。采用离散变异法,指明了染色体个体元素变异的基本字符,用设定的变异概率(Pm)对每个元素进行变异。本文取Pm=0.01。
(5)搜索终止条件。达到最优解连续不变最大代数MAX,或达到遗传操作的最大遗传代数MAXGEN。只要满足2个条件中任何1条搜索就结束。具体流程见图2。

图2 改进的算法流程图
优化过程中,设置种群的大小为NIND=100,MAX=50, MAXGEN=200;接入配电网的光伏发电项目的总容量为1 500~3 000 kVA,单个节点接入容量为100 kVA,光伏电源的功率因数λ=0.9。
3 算例分析
3.1 算例系统
采用文献[12]提供的标准IEEE33节点配电系统为例进行算例验证。潮流计算时取系统三相功率基准值Sb=10 MVA,线电压基准电压Ub=12.66 kV,33母线测试系统如3所示。

图3 IEEE33节点配电网测试系统拓扑图
3.2 目标函数的优化
寻优操作结束后,得出最优个体:
cap=[1 1 1 1 1 1 0 0 1 1 0 0 0 1 0
1 0 1 0 1 0 1 1 1 1 0 0 1 0 0 1 0]
(9)
式中:1表示在相应节点接入光伏电源;0表示在相应节点不接光伏电源。由于光伏电源对支路潮流的影响,可以看出大部分光伏电源都位于辐射线路的中末端或负荷较大的节点处。
3.2.1 配电网网损的优化
图4为标准配电系统接入DG前后各支路损耗的变化情况。可以看出DG接入配电网后,所有支路的有功功率损耗均比未接入DG有所下降,以2号支路最为明显,该支路有功功率损耗由45.61 kW下降到6.49 kW,下降了85.77%。而且,系统的总的网损也由191.88 kW下降到48.17 kW,下降了74.89%,降低了配电网网损率。据统计配电网网损占整个电力系统电能损耗的7%~8%,网损下降74.89%,这对电网节能降损具有重大的意义。

图4 DG接入配电系统前后各支路损耗的变化曲线
3.2.2 节点电压的优化
图5为标准配电系统接入DG前后各负荷节点电压的变化情况。可以明显地看出DG接入配电网后,各节点电压相比未接入DG有显著的提高,其中系统各节点电压的最小电压值(18号节点)由0.913 1(标么值)提高到0.931 2(标么值),显然DG的接入对配电网电压起到很好的支撑作用。也就是说在系统运行的时候,支路17-18为系统最薄弱的支路,当负荷增长因子(load scale factor,LSF)增大时,如果节点18的负荷增大更有可能导致系统发生电压崩溃,但是配电网接入了DG后提高了各节点电压值,尤其是对最小节点电压值的提高效果尤为明显,这样就极大地增强了系统承受负荷增长的能力,使得配电网更加安全可靠。

图5 DG接入配电系统前后各节点的电压变化曲线
3.2.3 接入费用最小的优化
表1为不同接入DG的方式产生的接入费用比较,第(1)、(2)组数据为随机接入1组DG产生的费用,分别是840万元和1 000万元,第(3)组数据为接入优化规划后的DG的费用,为720万元。后者明显要低于前两者,有效地降低了成本。
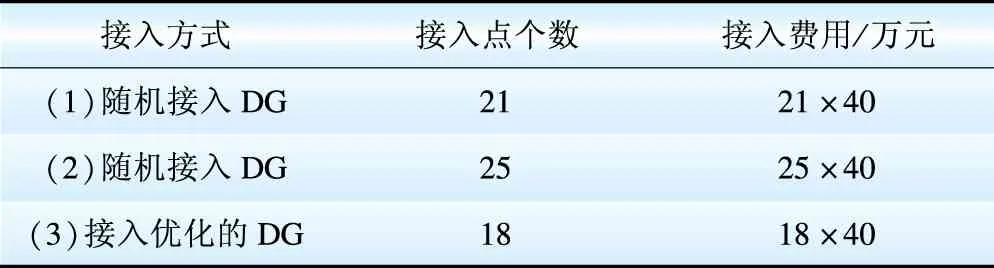
表1 接入DG的费用比较
3.2.4 3种情况下网损与节点电压的变化
为了更好地说明采用遗传算法对DG的位置和容量进行优化规划的必要性,图6以3种情况为代表,以支路损耗和节点电压为参考说明该问题。第1种情况是配电网接入优化后的DG,第2种是配电网接入随机的DG,第3种是配电网不接入DG。
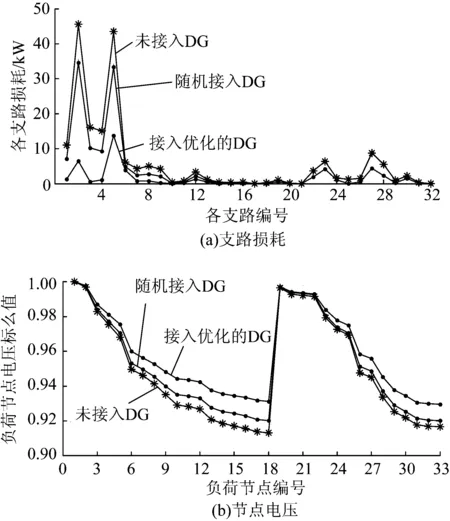
图6 接入优化的DG、随机接入DG以及不接入DG的3种情况下配电网网损和节点电压
对3种情况的2项参考结果分别进行比较,可以明显看出,第1种情况的各项数据最优,第2种情况的数据次之,第3种情况的数据相对前2组较差。网损具体数据分别为48.17,144.65,191.88 kW;配电网各节点电压的最小电压值分别为0.931 2, 0.920 3,0.913 1(标么值)。由此可见在配电网中接入DG时,对DG的位置和容量进行优化是非常有必要的。
3.3 改进的并列选择法
表2以标准IEEE33节点配电系统为例进行算例验证,列出了按标准的并列选择法和改进的并列选择法进行多目标寻优的结果。由表2可以看出,对于目标3两者优化的结果都是一样的;对于目标2标准方法略次于改进的方法,但2种方法配电网节点电压偏移最大值的差值仅为0.000 1,换算为有名值差值为0.001 3 kV,这对基准电压为12.66 kV的配电系统完全可以忽略不计;对于目标1,前者在142代收敛,而后者在107代收敛,且前者网损最小值为49.03 kW,后者网损最小值为48.17 kW,前者优化的结果明显优于后者。

表2 改进算法前后各目标函数值
为了更清楚地说明改进算法的优点,图7显示了改进算法前后对目标函数网损最小进行一次仿真得到的结果。可以看出未改进算法的寻优在152代收敛,改进算法的寻优在92代收敛,前者网损最小值为49.80 kW,后者网损最小值为48.17 kW,改进的算法在求目标函数的最优值时优于后者,而且收敛代数也远小于未改进的算法,效率更高。
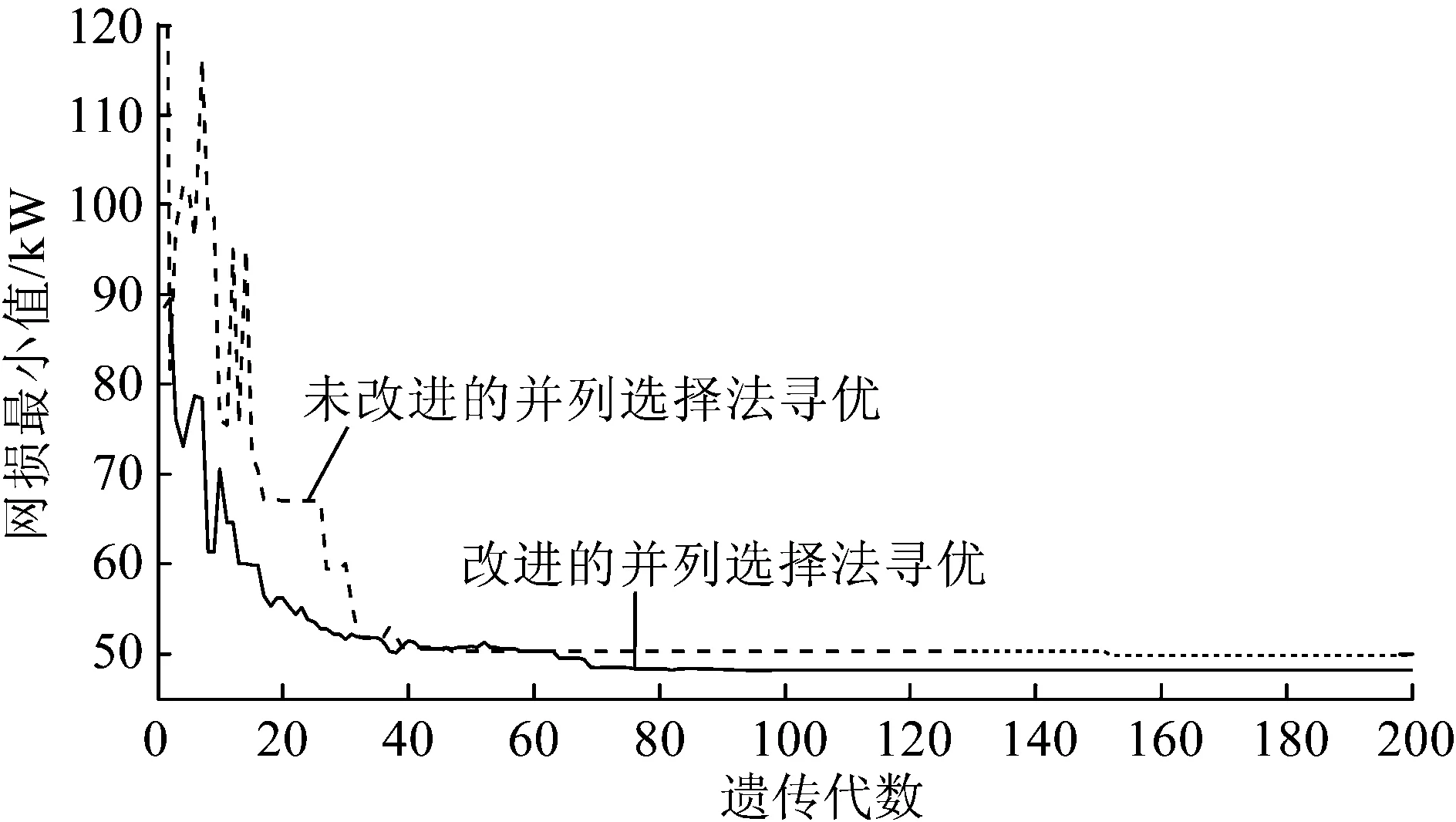
图7 改进算法前后网损最小的仿真结果
4 结 论
本文采用基于MATLAB的遗传算法工具箱,对光伏发电并网优化规划进行了仿真实验,得出以下结论:
(1)建立了以网络损耗最小、节点电压偏移最小和费用最小的多目标优化模型,对光伏电源的位置和容量进行最优规划,结果证明了该模型的正确性,对光伏发电接入配电网的规划设计具有很好的指导意义。
(2)在进行多目标最优求解时,提出的改进并列选择法相比标准并列选择法,能够突出重点优化的目标,不但寻优结果更准确,而且效率也更高。
[1]梁有伟,胡志坚,陈允平. 分布式发电及其在电力系统中的应用研究综述[J].电网技术,2003,27(1):71-75,88.
[2]王成山,王守相. 分布式发电供能系统若干问题的研究[J].电力系统自动化,2008,32(20):1-4.
[3]董慎学, 周羽生, 曹勋伟,等.含分布式电源的配电网线损电压研究[J].电力建设,2011,32(6):22-25.
[4]El-khattam W,Salama M M A. Distribution system planning using distributed generation[C]//Proceedings of IEEE Canadian Conference on Elcetrical and Computer Engineering.Montreal:IEEE,2003:579-582.
[5]崔凯, 李敬如, 赵娟. 法国配电网及其规划管理浅析[J].电力建设,2013,34(8):112-115.
[6]徐玉琴,李雪冬,张继刚. 考虑分布式发电的配电网规划问题的研究[J].电力系统保护与控制,2011,39(1):87-92.
[7]Conti S,Retiere N,Tina G.Small-scale embledded generation effect on voltage profile an analytical method[J]. IEE Proceedings Generation Transmission and Distribution,2003,150(2):78-86.
[8]王志群,朱守真,周双喜. 分布式发电对配电网电压分布的影响[J]. 电力系统自动化,2004,28(16):56-60.
[9]王成山,陈恺,谢莹华,等. 配电网扩展规划中分布式电源的选址和定容[J]. 电力系统自动化,2006, 30(3):38-43.
[10]颜伟,刘方,王官洁,等. 辐射型网络潮流的分层前推回代算法[J].中国电机工程学报,2003,8(23):76-80.
[11]雷英杰,张善文,李续武,等. MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2006.
[12]王守相,王成山. 现代配电系统分析[M]. 北京:高等教育出版社,2007.
(编辑:杨大浩)
OptimalAllocationofGrid-ConnectedPhotovoltaicGenerationBasedonImprovedGeneticAlgorithm
BAO Guangqing1, YANG Guojin1, YANG Yong2, CHANG Yong1
(1. Key Laboratory of Advanced Control for Industrial Process in Gansu Province, Lanzhou University of Technology,Lanzhou 730050, China; 2. Gansu Electric Power Research Institute, Lanzhou 730050, China)
Photovoltaic generation will become the mainstream of new distributed generation systems in the future. This paper studied the optimal allocation of grid-connected photovoltaic generation. The multi-objective optimization model was established for the position and capacity of photovoltaic power, with minimum network loss, minimum node voltage offset and minimum connecting cost; the improved parallel selection method was proposed based on genetic algorithm (GA); the key objectives of optimization were highlighted, each objective function was treated differently, and the optimal solution of model was obtained with using the improved algorithm, based on the power flow calculation with using forward-backward sweeping method. Finally, the model and algorithm were tested through the IEEE33 node example system, whose results proved the correctness of the model and the superiority of the improved algorithm.
photovoltaic generation; distribution network; power flow calculation; genetic algorithm; optimal allocation
国家自然科学基金项目(51267011);甘肃省杰出青年基金项目(1111RJDA007)。
TM 71
: A
: 1000-7229(2014)06-0013-05
10.3969/j.issn.1000-7229.2014.06.003
2013-12-05
:2013-12-28
包广清(1972),女,教授,博士生导师,主要研究方向为可再生能源发电与电能转换、电磁场数值计算与分析、现代电力传动系统设计;
杨国金(1985),男,硕士研究生,研究方向为分布式电源的并网控制, E-mail:eckyfcu@163.com;
杨勇(1968),男,高工,主要研究方向为电网调度及分布式发电并网及故障诊断;
常勇(1988),男, 硕士研究生,研究方向为电气设备故障诊断与信号处理。

