基于滑窗迭代DFT和小波包分析的谐波电流检测方法*

陈 勇， 田 丽， 赵明敏， 杜道昶

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

目前，由于大量的电力电子器件和非线性负载设备接入电网[1]，使电网中的谐波源激增.谐波可使电力设备产生过电压，造成设备故障[2]；使通信线路产生干扰,造成线路损坏；使电网的损耗加大，造成电能利用效率降低等[3].这给电力系统及接入其中的设备的正常运行带来了严重威胁，并对电能质量造成了不良影响.

对电网中的谐波问题进行治理，其前提条件就是对谐波进行检测和分析，因而精确的谐波检测可以作为谐波治理的良好的依据[4].传统的谐波检测方法离散傅立叶变换(DFT)运算过程是一个完整周期内的求和运算，其在时域无局部化特性，还存在着频谱混叠和栅栏效应等问题，不能达到电网谐波检测的要求.滑窗迭代DFT是在DFT的基础上改进得到的，可使系统的运算过程简化，具有较好的时频域特性，但当工频发生小幅振荡时其检测结果含有必不可免的误差.小波变换[5]拥有良好的时频域局部化特性，但其对信号频带的分解是非均匀的，结果出现低频频带窄、高频频带宽的特征，这就造成了高频信号的检测精度降低[6]，不利于精确地检测各次谐波.而小波包分析是在小波变换的基础上发展来的，其对信号进行均匀分解，不仅分解低频频带，还分解高频频带，因而具有更高的检测精度和更加出色的时频特性.现将滑窗迭代DFT和小波包分析的优点结合起来，给出了一种谐波检测组合方法，并利用MATLAB进行仿真验证其有效性.

1 滑窗迭代DFT算法的基本原理

1.1 DFT理论基础

已知周期为T的信号x(t)，且其带宽有限,频带宽度为基波角频率ω到Nmax*ω[7]，则其离散傅氏变换(DFT)的表达式：

(1)

式(1)中：

(2)

(3)

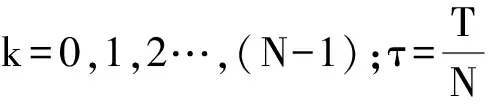
由上面的离散傅氏变换(DFT)公式知，它们的运算过程均需要固定的从(i=0)开始来进行计算，并且整个周期内N个采样点都包含在其中，造成运算量很大，故不能用来快速的检测基波和谐波分量.因此需要对上面的公式进行改进即滑窗迭代DFT算法.

1.2 滑窗迭代DFT算法

滑窗迭代DFT算法的基本思想是：将An和Bn看成一个整体变量，因而无需进行逐点求和运算，这样大大加快了运算速度.依据其基本思想，可对式(3)作下面的改进：

(4)

式中Ncur表示最新的采样数据点，x(iτ)表示i个采样周期前的采样数据[8]，由式(4)知，滑窗迭代DFT算法的新变化是用(i=Ncur)代替了(i=0)，(Ncur-N+1)代替了(N-1)，将采样的最新实时数据用于检测负载电流，同时又舍去了最老的采样数据，使系统的数据更新变得更加迅速，能够更加精准的跟踪负载电流信号的动态.由此可知，将上式化简可以得出基波电流分量：

x(kτ)=A1cos(ωkτ)+B1sin(ωkτ)

(5)

(6)

由式(6)可以看出，如要得到理想的实时基波电流分量，一定要在一个采样间隔周期内将A1和B1的值同时求出，但当系统采样点数(即N)很多时，式(6)的运算量也是非常大的.所以为了精简滑窗迭代过程的运算量，采用软件来完成滑窗迭代过程，算法模型如图1所示.

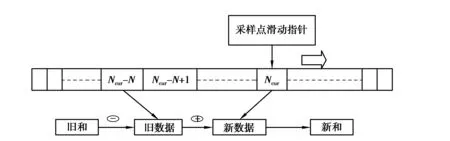
图1 滑窗迭代算法模型

由图1可知，在连续的数据存储单元内，存储着整周期内N个采样点数据与其对应的旋转因子相乘的结果，在运算过程中采样点滑动指针是用来指示当前采样数据的存储位置，当整周期内的N个采样点数据运算完成后，指针返回数据存储空间的起始位置，继续数据的周期循环更新[8].

式(6)中的求加运算可以简化成下面的式(7)、(8)来表示：

(7)

(8)

由式(7)、(8)的变换知，式(6)的求和运算过程就精简为一减一加的运算，再将运算得到的新和重新存储于旧和的数据存储空间中，实现迭代[9].因此，整个滑窗迭代运算过程只须在初始化阶段的一个工频周期内将整个周期的求和运算完成，后面的求和运算在一个采样周期内就可实现.因而，滑窗迭代算法用于分析谐波电流，可使系统的运算过程简化并提高其实时性.

滑窗迭代算法不仅可用于分析整个负载谐波，也可用于单次谐波的检测.现以7次谐波的检测为例：

x(kτ)=A7cos(ωkτ)+B7sin(ωkτ)

(9)

(10)

A7和B7的值也可以运用滑窗迭代算法来求出，再根据式(9)就能求得k时刻对应的7次谐波电流含量.

2 小波包分析的基本原理

小波包分析可以提供一种更加精密的信号分析方法，其对信号进行均匀分解，不仅分解低频频带，还分解高频频带，而且可以依据被分析信号的特性，自适应地选取合适的频带，使之与信号频谱相匹配[10]，以改善信号时频分解率.

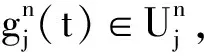
(11)

(12)

(13)

式(3)中hl-2k和gl-2k是小波包重构的低通和高通滤波器组[11].小波包分析分解后的每个频带的带宽均相同，而且每个频带中也含有相同的谐波次数.因此，将小波包分析应用在电网谐波的检测上，能够有效的分离出电网上的各次谐波含量.

3 方法实现框图

将滑窗迭代DFT和小波包分析组合起来，先用滑窗迭代DFT将负载电流信号中的基波分量和谐波分量分离，然后利用小波包对前面得到的谐波分量进一步分析，精确的分离出残余基波和各次谐波含量.方法流程见图2.

图2 方法框图

4 仿真实验与结果分析

为了验证方法的有效性，下面对所给方法进行仿真分析.电力系统中的理想负载电流信号为正弦周期信号，但由于大量非线性负载设备产生谐波接入电网，实际的信号均为不规则的非正弦周期信号，且谐波信号是随机的，时变的.给定了一个负载电流信号x(t)，其工频为50Hz，采样频率为1kHz，仿真时间为0.5s.其信号幅值在0.15s时幅值减少为原来的一半，0.24s时幅值变为原来的二倍，0.35s时变为原来的4倍.图3是用滑窗迭代DFT算法对负载电流信号进行检测得到的仿真图，x表示原始负载电流信号，xj表示基波信号，x-xj表示谐波信号.图4是用DFT对都负载电流信号进行分析得到的频谱波形图，它反映了负载电流信号中含有50Hz基波和5次，7次谐波以及基波和各次谐波的振幅.

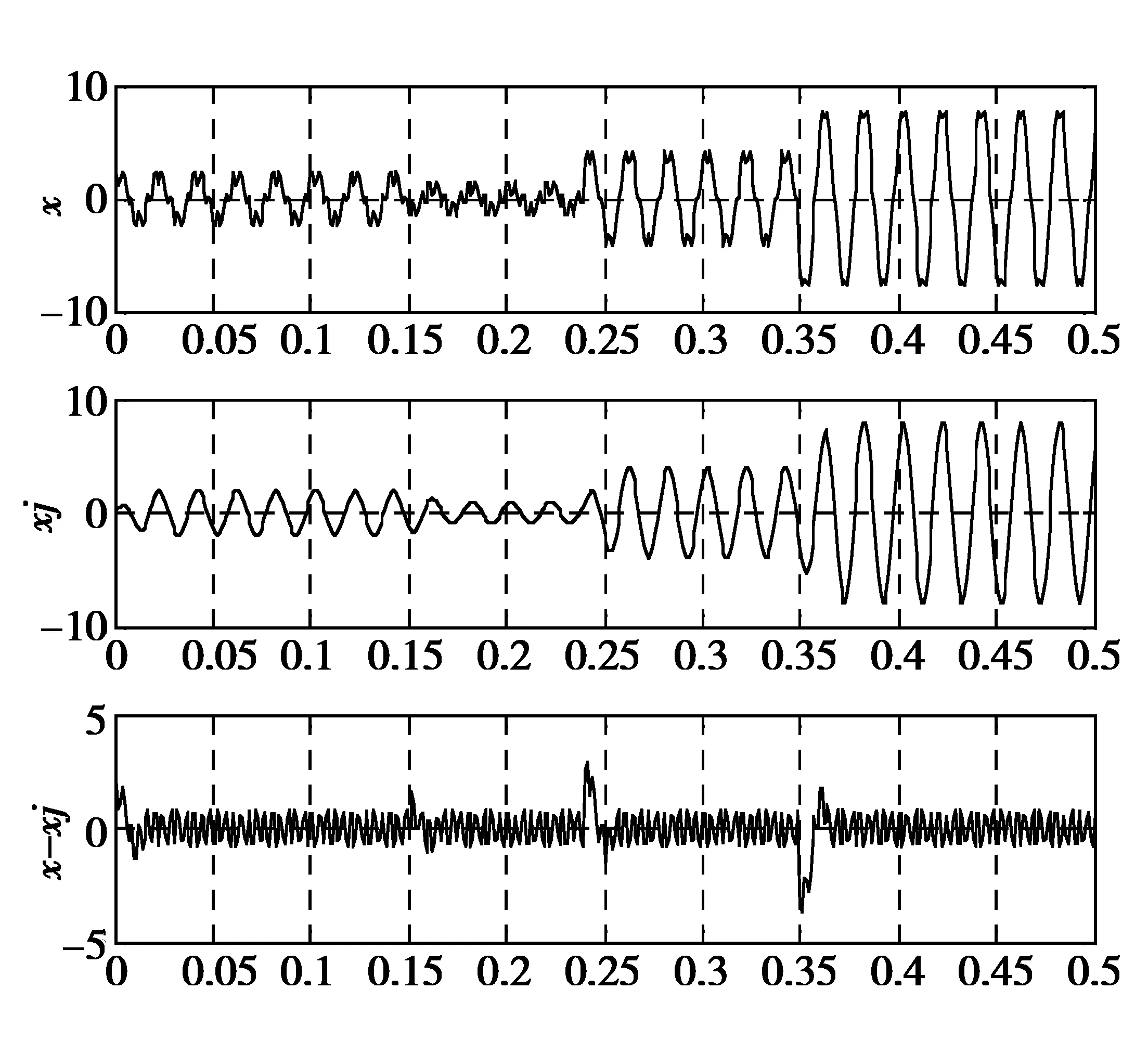
图3 滑窗迭代DFT检测仿真图

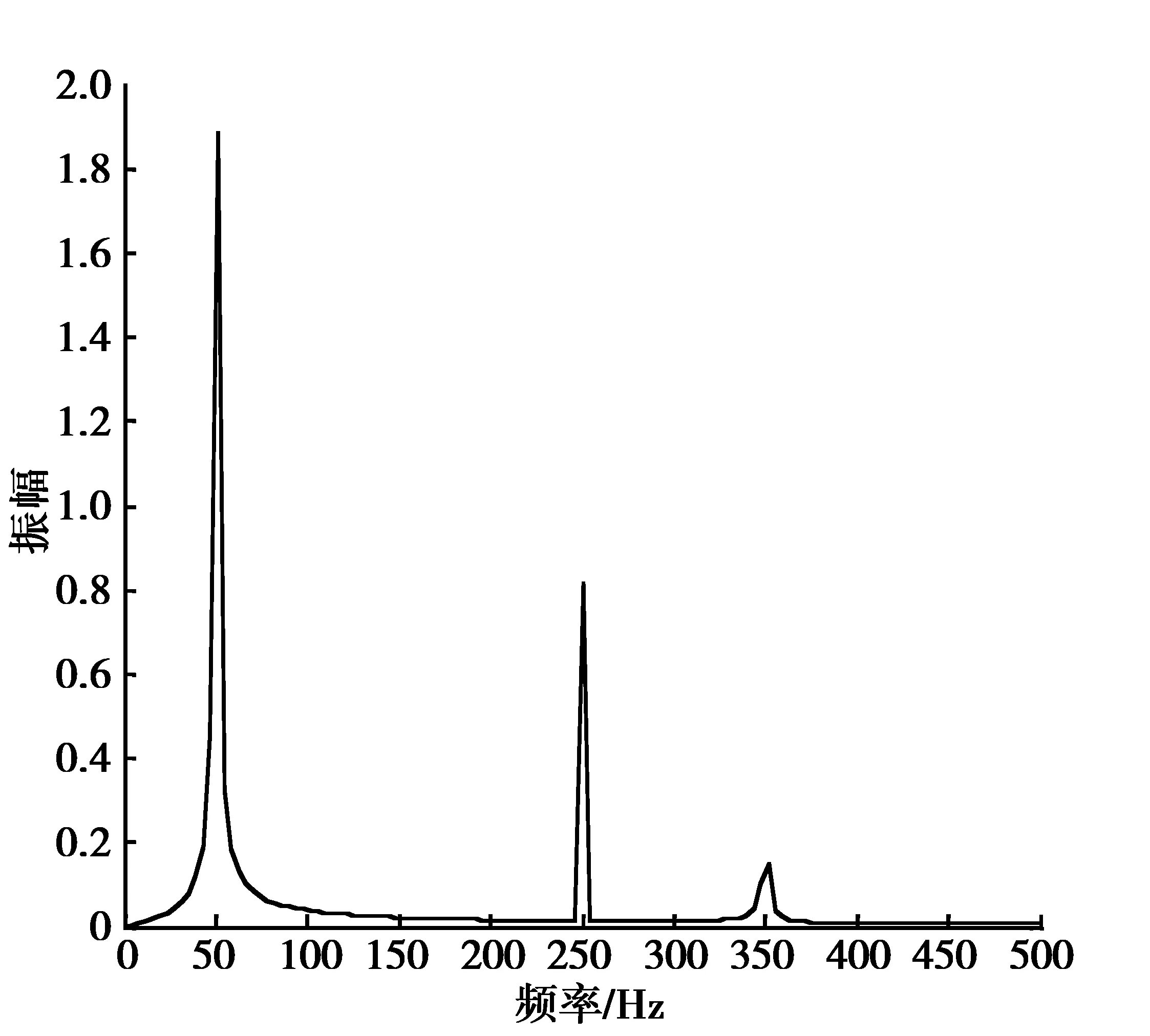
图4 DFT检测方法仿真图

将图3、4的仿真结果进行比较，从图4中可以看出DFT只是将负载电流信号转变为频域的信号，无法反映信号在时域的特征，如起始时刻，持续时间，以及突变点等.而从图3中的滑窗迭代DFT检测仿真图中可以看出方法能将负载电流信号中的基波(xj)和谐波分量(x-xj)分离开来，并且从基波的波形可以看出滑窗迭代DFT算法能够精准地在一个工频周期内跟踪负载电流信号的动态，在负载信号出现突变时能更好的反映其时域特征.因此，与传统DFT分析相比，滑窗迭代DFT检测算法，有着很明显的优势.

滑窗迭代DFT检测算法也有其必不可免地缺陷，由于在进行电流谐波分析时采用的方法是在计算得到基波电流分量后，再用负载电流分量减去它来得到谐波分量(x-xj)，因而得到的谐波分量是各次谐波之和.但在现实的电网中，工频不是始终保持在50 Hz而是围绕着50 Hz小幅波动，工频偏离了50 Hz时，会造成泄漏和栅栏效应，从而基波信号的幅值也会产生偏差，若再用负载电流信号减去此时的基波信号，那么检测到的谐波信号中肯定会有残余的基波信号成分，给检测过程造成一定的误差.

为了弥补滑窗迭代DFT检测算法的缺点，采用db40小波和shannon熵接着对滑窗迭代DFT检测出的谐波信号进行2层小波包分解，采样周期为1 000 Hz，生成的小波包分解树如图5，分解结果如图6.

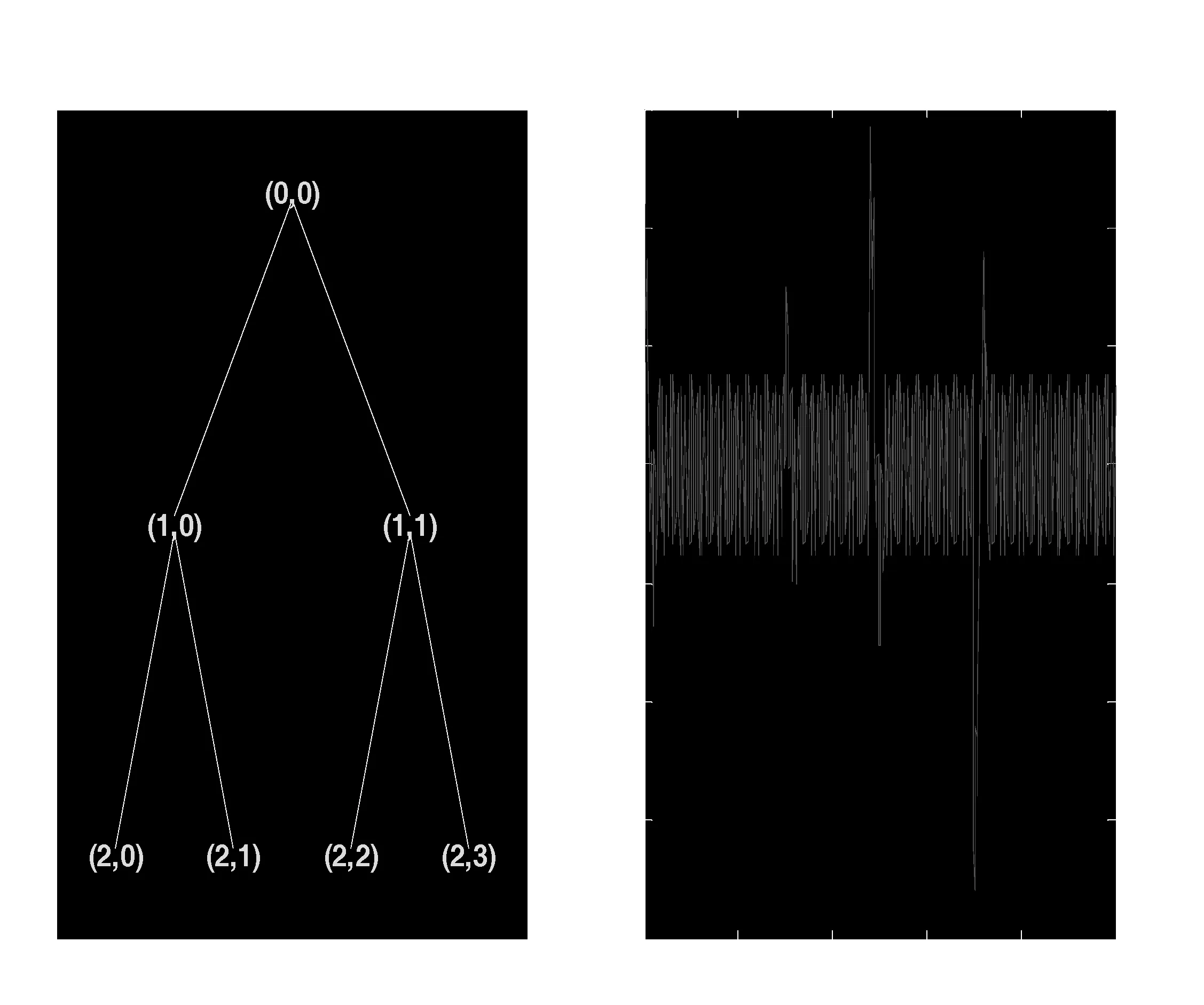
图5 二层小波包分解树仿真图

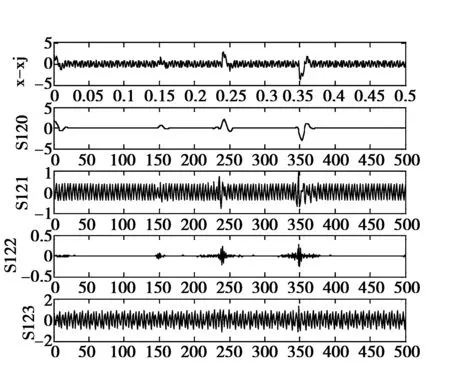
图6 用db40分解谐波信号仿真图

从图5可以看出，谐波信号的频带宽度被分成4个均匀子频带，即(2.0)，(2.1)，(2,2)，(2.3).谐波信号的频带宽度为500 Hz，则2层小波包分解分解后所占的频带分别为(2.0)0～125，(2.1)125～250，(2,2)250～375，(2.3)375～500 Hz；同时也可看出信号也发生了3次突变.从图6可知，S120(2.0)表示重构了的基波电流信号，表明滑窗迭代DFT算法得到的谐波信号之和中含有残余的基波电流信号成分.S123(2.3)和S121(2.1)分别表示重构的5次和7次谐波分量.从S122(2.2)中可以清楚的看出谐波电流信号在0.15、0.24、0.35 s处发生突变.由此可知，小波包分解能进一步的对谐波信号精确分析，将残余基波信号与各次谐波信号分离出来，同时能更好的的反映信号的突变点.

5 结束语

仿真实验结果表明，给出的滑窗迭代DFT和小波包分析组合算法充分的利用了这二种方法的优点，能够有效的分离出基波电流信号和各次谐波电流信号.因此，这验证了该组合算法的有效性，其能对电网中的负载电流信号进行准确检测，体现了信号检测的目标跟踪特性和实时性，可以为电网中谐波信号的治理作为一种前提参考.

参考文献：

[1] 张颖.电力系统谐波与电压扰动检测理论及方法研究[D].长沙：湖南大学，2010

[2] 叶永卫，邵阿红，田二明.供电电网谐波治理措施的探讨[J].重庆工商大学学报：自然科学版，2012,29(10):92-95

[3] 蒋雪峰，李 洁，张沥文，等.关于电力系统中两大谐波检测法的比较分析[J].现代电子技术，2010，313(2)：205-210

[4] 向东阳，王公宝，马伟明，等.基于FFT和神经网络的非整数次谐波检测方法[J].中国电机工程学报，2005，25(9)：35-39

[5] KEAOCHANTRANOND T, BOONSENG C. Harmonics and interharmonics estimation using wavelet transform [C]. IEEE/PES Transmission and Distribution Conference and Exhibition, Asia Pacific,2002：775-779

[6] 吴仕宏，王 宏，初国力，等.基于小波包变换的电力系统谐波检测[J].沈阳农业大学学报，2010，41(3)：372-374

[7] 李益华，段虎，周黎明.基于DFT滑窗迭代算法与小波变换的谐波检测方法[J].电测与仪表，2011，48：6-9

[8] 周柯，罗安，彭剑，等.基于滑窗迭代DFT的电力谐波检测[J].华北电力大学学报，2006，30(3)：27-30

[9] 陆秀令，周腊吾，张松华，等.电力谐波滑窗迭代DFT检测算法的研究与仿真[J].系统仿真学报，2008，20(2)：3 652-3 655

[10] 刘蓉晖.基于小波包变换的电力系统谐波检测[J].上海电力学院学报，2011，37(4)：337-340

[11] 张德丰.MATLAB小波分析[M].北京：机械工业出版社，2009