一类广义Busemann-Petty问题的稳定性

冯 伟

(重庆师范大学 数学学院，重庆 401331)

Busemann-Petty问题是凸几何学中著名的经典难题.它自提出便先后吸引了包括Fields奖获得者J.Bourgain在内的诸多优秀数学家投身到其研究之中.为了解决这一经典问题，数学家们极大地丰富了凸几何学的内容，并发展了许多新的凸几何学研究的方法.

1956年，著名几何学家H.Busemann和C.M.Petty提出Busemann-Petty问题[1]：如果对于Rn中的两个关于原点中心对称的凸体K，L,使得对于单位球面Sn-1上所有单位向量ξ,都有

voln-1(K∩ξ⊥)≤voln-1(L∩ξ⊥)

成立，其中voln-1(·)表示n维体积，ξ⊥={x∈Rn:=0}表示正交于ξ方向上的中心超平面，那么是否voln(K)≤voln(L)必然成立？

1975年，D.G.Larman和C.A.Rogers[2]证明了当n≥12时答案为否定的;1989年，K.Ball[3]证明了当n≥10时答案为否定的;1990年，A.Giannopoulos[4]和G.Bourgain[5]证明了当n≥7时答案为否定的;1992年，M.Papadimitrackis[6]证明了当n≥5时答案为否定的.

这个问题彻底被解决其实归功于E.Lutwak[7]的卓著工作—揭示截面体和Busemann-Petty问题之间存在重要的联系；基于这种联系，1994年，R.Gardner[8]证明了当n=3时Busemann-Petty问题的答案是肯定的；1999年，张高勇[9]证明了当n=4时Busemann-Petty问题的答案是肯定的.

1999年，R.Gardner，A.Koldobsky以及T.Schlumprecht[10]用Fourier变换给出了所有维数的Busemann-Petty问题的一个一致解；F.Barthe，M.Fradelicz和B.Maurey[11]给出了这个一致解的重要的证明；然后就出现了许多与Busemann-Petty问题相关联的有意义的结果.1996年，张高勇[12]首先研究了Busemann-Petty问题的一个几何推广：如果Rn中两个关于原点中心对称的凸体K和L满足

voli(K∩ξ)≤voli(L∩ξ),∀ξ∈G(n,i)

其中G(n,i)表示在Rn中的i维子空间的格拉斯曼流形，那么是否voln(K)≤voln(L)一定成立？

这个问题一般被称作广义Busemann-Petty问题.当i=n-1时，这个问题就是上述所提到的Busemann-Petty问题.已经证明了当33，i=2,3时的广义Busemann-Petty问题的解仍然是公开的(i=1时是明显成立的).

此处研究了广义Busemann-Petty问题一般的稳定性，结果或许对于广义Busemann-Petty问题的公开情形提供了启示.以下是主要结果及推论.

定理1 如果Rn上的一个(i,k)截面体K和一个星体L，对于任意的ξ∈G(n,i)都满足voli(K∩ξ)≤voli(L∩ξ)+ε，那么对于任意的η∈G(n,i+k)就有

在定理1中,k=n-i时的结果就是Koldobsky和马丹在文献[13]中确立的结果.

推论1 如果R4上的一个2维截面体K以及一个星体L，对于任意的ξ∈G(4，2)满足

vol2(K∩ξ)≤vol2(L∩ξ)+ε

(1)

那么就有

(2)

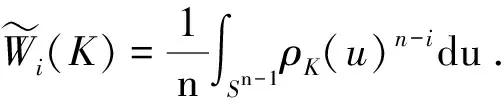
定理2D(n-i,r)={j∈N∩{0}:j

voli(K∩ξ)≤voli(L∩ξ)+ε

(3)

那么对于任意的j∈D(n-i,r)，就有

当j=0以及r=n-i时，定理2就得到Koldobsky和马丹在文献[13]中的结果.

推论2 如果R4中的一个3维截面体K和一个星体L，对于任意的ξ∈G(4,3)，满足：

vol3(K∩ξ)≤vol3(L∩ξ)+ε

那么就有

(4)

回顾到式(1)和式(3)的条件中，和ε相乘的系数都是1，但是在式(2)和式(4)中，和ε相乘的系数却都是小于1的.因此，推论1和推论2实际上从直观上启示了张高勇的广义Busemann-Petty问题的公开情形或许是有正解的.

参考文献：

[1] BUSEMANN H, PETTY C M. Problem on Convex Bodies[J].Math Scand,1956(4): 88-94

[2] LARMAN D G, ROGERS C A. The Existence of a Centrally Symmetric Convex Body With Central Sections That Are Unexpectedly Small[J]. Mathematika,1975(22): 164-175

[3] BALL K. Some Remarks on the Geometry of Convex Sets, Geometric Aspects of Functional Analysis[J]. Ann Math, 1988(17): 224-231

[4] GIANNOPOULOS A A. A Note on a Problem of H. Busemann and C. M. Petty Concerning Sections of Symmetric Convex Bodies[J]. Mathematika, 1990(37):239-244

[5] BOURGAIN J. On the Busemann-Petty Problem for Perturbations of The Ball[J].Geom Funct Anal, 1991(1):1-13

[6] PAPADIMITRAKIS M. On the Busemann-Petty Problem about Convex, Centrally Symmetric Bodies in Rn[J]. Mathematika, 1992(39): 258-266

[7] LUTWAK E. Intersection Bodies and Dual Mixed Volumes[J]. Adv Math, 1988(71): 232-261

[8] GARDNER R J. A Positive Answer to the Busemann-Petty Problem in Three Dimensions[J]. Ann Math, 1994(140): 435-447

[9] ZHANG G. A Ppositive Answer to the Busemann-Petty Problem in Four Dimensions[J]. Ann Math, 1999(149): 535-543

[10] GARDNER R J, KOLDOBSKY A, SCHLUMPRECHT T. An Analysis Solution to the Buseman-Petty Problem on Sections of Convex Bodies[J]. Ann Math， 1999(149): 691-703

[11] BARTHE F， FRADELIZI M， MAUREY B. A Short Solution to the Busemann-Petty Problem[J]. Positivity,1999(3): 95-100

[12] ZHANG G. Section of Convex Bodies[J]. Am J Math, 1996(118): 319-340

[13] KOLDOBSKY A, MA D. Stability and Slicing Inequalities for Intersection Bodies[J]. Geom Funct Anal， 2013(162):325-335