一类推广的迭代泛函微分方程的光滑解

刘 佳

(山东城市建设职业学院 建筑经济管理系，济南 250103)

0 引 言

自Jack Hale的工作[1]发表后，关于泛函微分方程解的研究已有许多工作.形如

x′(t)=H(x(0)(t)，x(1)(t)，…，x(m)(t))

的迭代泛函微分方程，被许多人讨论过，这里x(0)(t)=t，x(1)(t)=x(t)，…，x(k)(t)=x(x(k-1)(t))， k=2，…，m.确切地说，Eder[2]考虑了泛函微分方程x′(t)=x(2)(t)，证明了该方程的每一个解或者恒为零或者严格单调.在文献[3， 4]中，Feckan与王克在不同条件下研究了方程

x′(t)=f(x(2)(t))

(1)

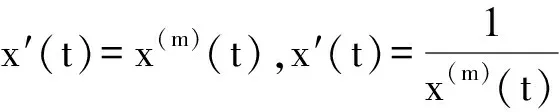
(2)

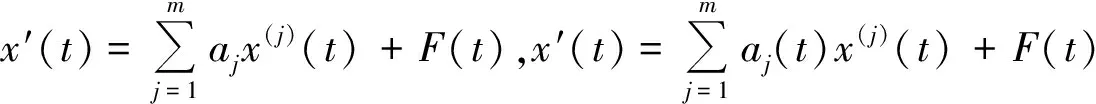
此处利用不动点定理考虑一类更为广泛的迭代泛函微分方程

(3)

光滑解的存在性.显然，当f(t)=1时，式(2)是式(3)的特殊形式.那么，对于式(2)的光滑解的研究便可以看成是此处结论的特殊形式.

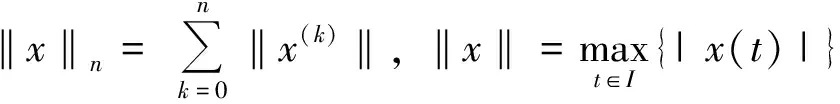
Ω(M1，…，Mn+1；I)={x∈Cn(I，I)：|x(i)(t)|≤Mi，i=1，2，…，n

|x(n)(t1)-x(n)(t2)|≤Mn+1|t1-t2|，t，t1，t2∈I}

为了便于书写，记

xij(t)=x(i)(x(j)(t))，x*jk(t)=(x(j)(t))(k)

其中i，j，k是非负整数.为了寻找式(2)在Cn(I，I)中的解x(t)，使得x(ξ)=ξ，自然会想到在区间[ξ-δ，ξ+δ]中考虑，其中δ>0.定义

Ψ(ξ；η0，…，ηn-1；N1，…，Nn；I)={f∈Ω(N1，…，Nn；I)：f(i)(ξ)=ηi，i=0，1，…，n-1}

X(ξ；ξ0，…，ξn；1，M2，…，Mn+1；I)={x∈Ω(1，M2，…，Mn+1；I)：x(ξ)=ξ0，x(i)(ξ)=ξi，i=1，2，…，n}

其中 ξ0=ξ.

由数学归纳法，对k=0，1，…，n，可以证明

x*jk(t)=Pjk(x10(t)，…，x1，j-1(t)；…；xk0(t)，…，xk，j-1(t))

(4)

(5)

(6)

其中Pjk是系数为非负数的唯一多项式，式(4)-(6)的证明可在文献[8]中找到，I是R上的闭区间.

1 主要定理

这一部分，证明方程(3)光滑解的存在性定理，需要用到下面的事实：对x(t)，y(t)∈X，有

|x(j)(t1)-x(j)(t2)|≤|t1-t2|，t1，t2∈I，j=0，1，…，m

(7)

‖x(j)-y(j)‖≤j‖x-y‖，j=1，2，…，m

(8)

‖x-y‖≤δn‖x(n)-y(n)‖

(9)

不等式(7)-(9)的证明可在文献[9]中找到.

定理1 设I=[ξ-δ，ξ+δ]， 这里ξ，δ满足

(10)

且f∈Ψ(ξ；η0，…，ηn-1；N1，…，Nn；I)，则式(3)在

X(ξ；ξ0，…，ξn；1，M2，…，Mn+1；I)

中有解，其中

(i)

(11)

(12)

其中，k=2，3，…，n；s1+2s2+…+(k-j-1)sk-j-1=k-j-1；s=s1+s2+…+sk-j-1.

(ii)

(13)

其中，k=2，3，…，n；s1+2s2+…+(k-j-1)sk-j-1=k-j-1；s=s1+s2+…+sk-j-1.

(iii)

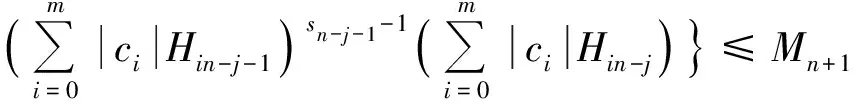
(14)

其中，s1+2s2+…+(n-j-1)sn-j-1=n-j-1，s=s1+s2+…+sn-j-1.

证明利用Schauder不动点定理来完成证明，定义算子

(15)

先证对∀x∈X，有Tx∈X.由式(10)知

(16)

因此，(Tx)(I)⊆I.由FaàdiBruno公式易知

(17)

(18)

其中，k=2，3，…，n；s1+2s2+…+(k-j-1)sk-j-1=k-j-1；s=s1+s2+…+sk-j-1.再注意到(Tx)(ξ)=ξ，及式(11)(12)，有

(19)

(20)

其中，k=2，3，…，n；s1+2s2+…+(k-j-1)sk-j-1=k-j-1；s=s1+s2+…+sk-j-1.

因此，(Tx)(k)(ξ)=ξk，k=0，1，…，n.又因为

(21)

由式(13)(14)有

(22)

其中，k=2，3，…，n；s1+2s2+…+(k-j-1)sk-j-1=k-j-1；s=s1+s2+…+sk-j-1.

(23)

到此，证明了T是一个将X映到自身的算子.

现在证明T的连续性.设x，y∈X，则

‖Tx-Ty‖n=

(24)

经过计算，可以找到一列正数Pk使得

(25)

因此

‖Tx-Ty‖n≤

Γ‖x-y‖n

(26)

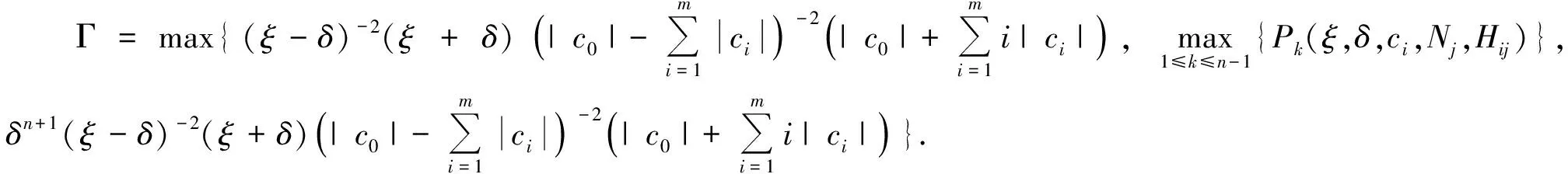
(27)

对式(27)两端求导即可看出x是式(3) 的解.定理证毕.

注意到，如果上面定理中有Γ<1，则表明 T是一个压缩算子.因此，上面证明中的不动点x必是唯一的.进一步可证这个唯一解关于给定的函数f是连续依赖的，即有定理2.

定理2 在定理1的条件下，且Γ<1，则方程(3)在

X(ξ；ξ0，…，ξn；1，M2，…，Mn+1；I)

中的唯一解连续依赖于给定的f.

参考文献：

[1] EDER E. The Functional Differential Equations[J]. J.Differential Equations， 1984(54)390-400

[2] FECKAN E. On Certain Type of Functional Differential Equations[J]. Math Slovaca， 1993(43)：39-43

[3] HALE J. Theory of Functional Differential Equations[M]. New York：Springer Verlag， 1977

[4] STANEK S. On Global Properties of Solutions of Functional Differential Equation[J]. Dynam Systems Appl， 1995(4)：263-278

[5] SI J G， LI W R， CHENG S S. Analytic Solutions of An Iterative Functional Differential Equation[J]. Comput Math Appl， 1997， 33(6) ：47-51

[6] SI J G， CHENG S S. Smooth Solutions of A Nonhomogeneous Iterative Functional Differential Equation[J]. Proceedings of the Royal Society of Edinburgh， 1998， 128(A)：821-831

[7] SI J G， WANG X P. Smooth Solutions of An Nonhomogeneous Iterative Functional Differential Equation with Variable Coefficients[J]. J Math Anal Appl， 1998(226)：377-392

[8] SI J G， ZHANG W N. Analytic Solutions of A Class of Iterative Functional Differential Equation[J]. Journal of Computational and Applied Mathematics， 2004(162)：467-481

[9] WANG K. On the Equation Funkcial Ekvac Skolink M I. Radar Handbook[M]. New York：McGraw-Hill， 1990

[10] ZHAO H Y. Smooth Solutions of a Class of Iterative Functional Differential Equations[J]. Abstract and Applied Analysis， 2012(12)：1-13

[11] ZHAO H Y.一类迭代泛函微分方程的光滑解[J]. 理论数学， 2012(2)：138-143