非凸混合向量均衡问题近似解的最优性条件*
龙宪军, 龚高华
(1.重庆工商大学 数学与统计学院,重庆 400067;2.重庆市綦江区东溪中学,重庆 401434)
近年来,向量均衡问题受到国内外许多学者的广泛关注,作为一种广泛的数学模型,向量均衡问题包括向量优化、向量变分不等式、向量互补以及向量鞍点问题等特殊情形, 而向量均衡问题研究中的一个非常重要的课题是研究其各种解的最优性条件. 在局部凸空间中,Gong[1]利用锥凸性获得了带函数约束的向量均衡问题解的最优性条件. Long等[2]在近似锥次类凸性假设下获得了带函数约束的向量均衡问题Henig真有效解的最优性条件,该结果改进了文献[1]中对应的结果. Gong[3]在Banach空间中利用非线性标量化函数和Ioffe次可微概念获得了非凸向量均衡问题弱有效解、Henig真有效解、超有效解以及全局真有效解的最优性条件. 众所周知,优化问题在非紧的情况下,解集往往是非空的. 然而其近似解集在很弱的条件下都是非空的且利用数值算法求得的解大多是近似解. 因此,研究近似解不仅具有理论价值而且有实际意义. 最近,龙宪军[4]获得了非凸向量均衡问题各种近似真有效解的最优性条件. 此处借助Mordukhovich次可微概念,在没有任何凸性条件下获得了混合向量均衡问题近似弱有效解的必要最优性条件. 此处所得结果推广了文献[4]中对应的结果.
1 预备知识
假设X和Y是两个Banach空间,X和Y的拓扑对偶分别为X*和Y*. 令C为Y中的闭凸点锥,记BX为X中的闭单位球,设K是X中的非空子集,记δK为集合K的指标函数,设K是X中的开凸子集,G为K的稠密子集,Banach空间X称为Asplund空间,如果每一个定义在K上的连续凸泛函在G上每一点处都是Frechet可微的,X是Asplund空间当且仅当X的每个可分子空间的对偶空间是可分的.
令C*={f∈Y*:f(x)≥0,∀y∈C} 为C的共轭锥. 设K为X的非空子集,用intK和clK分别表示集合K的拓扑内部和拓扑闭包.
设K为X的非空子集, 设x∈clK. 称集合
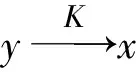
为K在点x0处的Mordukhovich法向锥.
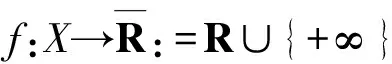
domf:={x∈X:f(x)<∞}
epif:={(x,t)∈X×R:f(x)≤t}
分别为f的有效域和上图像,称映射f为真的,如果domf≠∅.
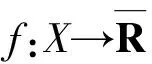
∂Mf(x0)={x*∈X*:(x*,-1)∈NM(epif;(x0;f(x0)))}
称集合∂Mf(x0)为映射f在点x0处的Mordukhovich次微分,显然,NM(K;x0)=∂MδK(x0). 如果x0∉ domf,则∂Mf(x0)=∅. 如果f是凸函数,则f的Mordukhovich次微分与凸分析中的次微分是一致的.

∂M(f1+f2)(x0)⊂∂Mf1(x0)+∂Mf2(x0)
引理2[5]设X和Y是两个Asplund空间,假设映射f:X→Y在x0是严格Lipschitz的,函数φ:Y→R在f(x0)附近是Lipschitz的,则

引理3[6]设C是Y中的闭凸点锥,e∈intC. 泛函φe:Y→R定义为
φe(y)=inf{t∈R:y∈te-C}
则φe是连续的次线性泛函,且对任意的t∈R,有
{y∈Y:φe(y) {y∈Y:φe(y)≤t}=te-C 而且,φe是严格intC-单调的. 定义1[7]设f:X→R是实值函数,ε≥0,称向量x∈K为标量优化问题inf {f(x):x∈K}的ε-拟最优解,如果 f(x0)≤f(x)+ε‖x-x0‖,∀x∈K 设K是X中的非空子集,假设F:K×K→Y,f:K→Y是两个向量值映射,考虑混合向量均衡问题(简记为MVEP):找x∈K,使得 F(x,y)+f(y)-f(x)∉-A,∀y∈K 其中A∪{0}为Y中的凸锥. 定义2 设ε≥0, 设intC≠∅ 以及e∈intC,称x∈K为 问题(MVEP)的εe-拟弱有效解,若 F(x,y)+f(y)-f(x)+ε‖y-x‖e∉-intC,∀y∈K 记问题(MVEP)的εe-拟弱有效解为WE(F,f,K,εe). 当x0∈K取定时,用Fx0(x)表示一元向量值映射,Fx0(x):X→Y定义为 Fx0(x):=F(x0,y),∀y∈K 定理1 设X和Y是两个Asplund空间,K是X中的非空闭集,intC≠∅ 以及e∈intC. 假设x0∈WE(F,f,K,εe)且满足F(x0,x0)=0,映射Fx0和f是严格Lipschitz的,则存在y*∈C*{0}和z*∈C*{0},使得 0∈∂M(y*∘Fx0)(x0)+∂M(y*∘f)(x0)+NM(K;x0)+εBX* 证明设x0∈WE(F,f,K,εe),则 F(x0,y)+f(y)-f(x0)+ε‖y-x0‖e∉-intC,∀y∈K 由引理3可得 φe(F(x0,y)+f(y)-f(x0)+ε‖y-x0‖e)≥0,∀y∈K 由于φe是次线性泛函,故 φe(F(x0,y))+φe(f(y)-f(x0))+ε‖y-x0‖≥0,∀y∈K 注意到φe(F(x0,x0))=0,从而x0是如下标量优化问题式(1)的ε-拟最优解 Minh(x)+φe(g(x)),s.t.x∈K (1) 特别地,x0是如下标量优化问题式(2)的最优解 Minh(x)+φe(g(x))+ε‖x-x0‖,s.t.x∈K (2) 其中h(x)=φe(Fx0(x)),g(x)=f(x)-f(x0),x∈X. 因此,x0是如下无约束优化问题式(3)的最优解 Minh(x)+φe(g(x))+ε‖x-x0‖+δK(x) (3) 由于φe是连续的凸函数,故其为局部Lipschitz的. 又因Fx0和f是严格Lipschitz的,故h和φe∘g也是局部Lipschitz的. 另一方面,由于集合K是闭的,则δK是真下半连续的. 由引理1,2以及文献[5]中的命题可得 0∈∂M(h(·)+(φe∘g)(·)+ε‖·-x0‖+δK(·))(x0)⊂ ∂M(φe∘Fx0)(x0)+∂M(φe∘g)(x0)+∂MδK(x0)+εBX*⊂ ∪y*∈∂Mφe(Fx0(x0))∂M(y*∘Fx0)(x0)+∪z*∈∂Mφe(0)∂M(z*∘f)(x0)+NM(K;x0)+εBX* 因此,存在y*∈∂Mφe(Fx0(x0))和z*∈∂Mφe(0),使得 0∈∂M(y*∘Fx0)(x0)+∂M(z*∘f)(x0)+NM(K;x0)+εBX* 由于φe是严格intC-单调的和凸的,因此很容易证明y*∈C*{0}以及z*∈C*{0}. 注1 如果f=0,则定理1退化为文献[4]中的定理1. 因此,定理2推广了文献[4]中的定理4.1. 参考文献: [1] GONG X H. Optimality Conditions for Vector Equilibrium Problems[J]. J Math Anal Appl,2008(342):1455-1466 [2] LONG X J,HUANG Y Q,PENG Z Y. Optimality Conditions for the Henig Efficient Solution of Vector Equilibrium Problems with Constraints[J]. Optim Lett,2011(5):717-728 [3] GONG X H. Scalarization and Optimality Conditions for Vector Equilibrium Problems[J]. Nonlinear Anal,2010(73):3598-3612 [4] 龙宪军.Asplund空间中非凸向量均衡问题近似解的最优性条件[J].数学物理学报,2014,34(A):2-4 [5] MORDUKHOVICH B S. Variational Analysis and Generalizd Differentiation[M]. Berlin:Springer,2006 [6] GERTH(TAMMER) C,WEIDNER P. Nonconvex Separation Theorems and Some Applications in Vector Optimization[J]. J Optim Theory Appl,1990(67):297-320 [7] LORIDAN P. Necessary Conditions for ε-optimality[J]. Math Program Study,1982(19):140-1522 主要结果


