模糊本体中的模糊相似度计算*

赵白露， 高 炜

(1.滨州职业学院 信息工程学院，山东 滨州 256603；2.云南师范大学 信息学院，昆明 650500)

本体(Ontology) 一词来源于哲学领域，起初是用来描述事物的性质和联系。在被引入计算机领域后，本体作为一种知识表示模型广泛应用于信息查询等各种计算机应用中。相关研究可参考文献[1，2]。但是，传统的本体只能表示确定的知识，从而限制了本体的应用。模糊本体作为本体模型的扩展，可以很好地处理日常生活中广泛存在的不确定知识，进而得到了广泛的关注，并成为近几年来研究的热点。相关研究可参考文献[3-6]。模糊本体应用的本质是计算模糊概念之间的模糊相似度。

1 新模糊本体模糊相似度计算算法

1.1 模糊本体概念

一般意义上的本体可以用一个三元组来表示：O=(C，P，R)，其中C是概念集合，P是属性集合，R是概念之间的关系集合。模糊本体由于用来描述不确定性知识，因此对应的概念集合和关系集合为模糊概念集合和模糊关系集合。即O=(Cf，P，Rf)，其中Cf={o1d1，…，ondn}为模糊概念集合，oi为概念，di是oi隶属与集合Cf的隶属度，因此这里d可理解为隶属度函数；模糊关系Rf⊆P(A1)×…×P(Am)是模糊元组的有限集合，其中Ai是属性集，P(Ai)表示Ai的幂集合。

1.2 模糊边权重计算

类似于一般本体图，模糊本体也可以用一个图来表示，称为模糊本体图。很多情况下这种模糊本体图为有向层次图。本文算法的第一步是计算模糊本体图中每条边的模糊权值。设vi，vj是模糊本体图中两顶点，分别对应模糊概念oi，oj。若vi，vj之间存在边eij，则该边的权值ω(eij)由两模糊概念的语义权值和描述权值决定：

ω(eij)=αsemaωsenantic(eij)+αdescωdescription(eij)

(1)

其中αsema+αdesc=1，ωsenantic(eij)表示语义权值，由基于实例的权值ωinstance(eij)和启发式权值ωheuristic(eij)按照如下加权法则得到：

ωsenantic(eij)=αinsωinstance(eij)+αheuωheuristic(eij)

(2)

其中αins+αheu=1；基于启发式的权值ωheuristic(eij)由领域专家根据领域公理给出。ωinstance(eij)根据两顶点对应实例的关系得到：

(3)

ωdescription(eij)是描述权值，它可根据关系权值和属性权值的加权得到：

ωdescription(eij)=αattωattribute(eij)+αrelωrelation(eij)

(4)

其中αatt+αrel=1。且

(5)

(6)

由此得到模糊权值矩阵W，其元素Wij即为ω(eij)。由此可知，W是对称矩阵。

1.3 计算模糊拉普拉斯矩阵对应次小特征值的特征向量

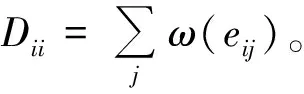
(7)

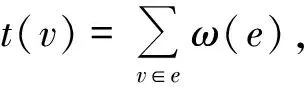
1.4 算法整体描述

由以上分析可以得到模糊本体相似度计算和模糊本体映射算法如下：

算法1：模糊本体模糊相似度计算算法

步骤1：信息的预处理。将模糊本体图中每个顶点的信息用一个向量表示；

步骤2：通过式(1)-式(6)计算边的模糊权重，从而得到模糊权值矩阵W；

步骤3：计算模糊拉普拉斯矩阵次小特征值对应的特征向量，进而将所有模糊概念映射到实数轴；

步骤4：给出模糊本体图G中每对模糊概念顶点对应实数的差值，由此判定它们的模糊相似程度。

算法2：模糊本体模糊映射算法

步骤1：信息的预处理。设模糊本体图G1，G2，…，Gm分别对应模糊本体O1，O2，…，Om，令G=G1+G2+…+Gm，将组合模糊图G中每个顶点的信息用一个向量来表示；

步骤2：通过式(1)-式(6)计算边的模糊权重，从而得到组合模糊图G的模糊权值矩阵W；

步骤3：计算组合模糊图G模糊拉普拉斯矩阵次小特征值对应的特征向量，进而将所有模糊概念映射到实数轴；

步骤4：给出组合模糊图G中来自不同分支的模糊概念对所对应的实数差值，由此判定它们的模糊相似程度。同时选择适当的本体模糊映射策略。

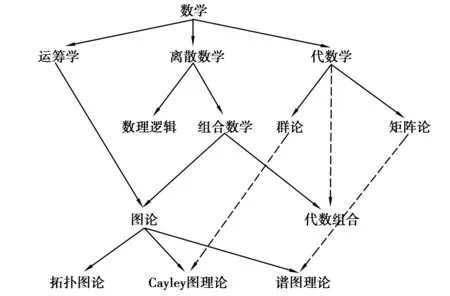
图1 “数学学科”模糊本体结构图

2 实验分析

本试验对文献[7]中构建的“数学学科”本体进行模糊化，如图1所示。由于模糊本算法是通过比较两个模糊概念对应实数的差来判断两个模糊概念的模糊相似度，因此本文算法得到的是相对模糊相似度而非绝对模糊相似度。由此采用传统的P@N[8]准确率对实验精确度进行评价，即首先由领域专家主观评价某模糊概念在本体中模糊相似度最高的的前N个概念，然后由算法计算出与该模糊概念模糊相似度最高的N个概念，看是否与领域专家的评判一致，计算准确率。在图1中，实线箭头代表模糊整体部分关系，虚线箭头代表模糊继承关系。

最后通过计算得到P@1的平均准确率为46.15%，P@3的平均准确率为58.97%，P@5的平均准确率为70.77%. 因此可以判定本文提出的模糊本体模糊相似度计算方法是有效的。

3 总 结

本文在模糊本体的框架下，得到一种新的计算模糊相似度的算法，通过边的权重并利用边的模糊关系得到模糊相似度。该算法最大的优点在于它的直观性。所有模糊概念被最终映射到实直线，两模糊概念之间的模糊相似度直接通过对应实数之间的差值得到。通过具体实验说明本文算法对特定的应用领域具有较高的效率。

参考文献：

[1] 高炜，梁立，徐天伟，周菊香. 半监督k-部排序算法及在本体中的应用[J]. 中北大学学报：自然科学版，2013，34(2)：140-146

[2] 高炜，朱林立，梁立. 基于图正则化模型的本体映射算法[J]. 西南大学学报：自然科学版，34(3)：118-121

[3] KANG D. Description Logics for Fuzzy Ontologies on Semantic Web[J]. Journal of Southeast University，2006，22(3)：343-347

[4] 杨青，陈薇，闻彬. 面向语义信息查询的模糊本体模型[J]. 计算机工程， 2010，36(8)：188-190

[5] 李慧琳，刘宁，李冠宇. 模糊本体构建的概念距离聚类方法[J]. 计算机工程与设计，2012，33(4)：1538-1541

[6] LIU J，MA Y，TANG S，et al. Chinese Fuzzy Ontology Mapping Based on Support Vector Machine[J]. China Communications，2012(3)：134-144

[7] 高炜，梁立，张云港. 基于图学习的本体概念相似度计算[J].西南师范大学学报：自然科学版，2011，36(4)：64-67

[8] CRASWELL N，HHWKING D. Overv iew of the TREC 2003 Web T rack[C]. Proceedings of the Twelfth Text Retrieval Conference. Gaithersburg：NIST Special Publication，2003：78-92