从三个角度证明点到平面的距离公式*

咸 伟 志

(重庆师范大学 数学学院，重庆 401331)

1 预备知识

在证明点到平面的距离公式前，先引入以下预备知识.

定义1[1](点到平面的距离) 一点与平面上的点之间的最短距离，叫做点到平面的距离.

定理1[1](平面基本定理) 空间中任一平面π的一般方程为Ax+By+Cz+D=0(A，B，C不全为0)，且向量{A，B，C}是平面π的一个法向量.

下面将分别从数学分析、高等代数和解析几何这3门课程的角度围绕点到平面的距离问题展开证明.受篇幅所限，在证明过程中所涉及的学科内容均将其作为定理提出，不再赘以证明.

2 数学分析的角度

2.1 问题的表述与涉及的内容[2]

问题的表述1 从数学分析的角度，点到平面的距离问题可叙述为：求平面π：Ax+By+Cz+D=0上的点到空间一点P(x0，y0，z0)的最短距离.问题实质上可以看成是求点与点的距离在某约束条件下的极值问题，即条件极值问题.在解决条件极值问题时，引入拉格朗日乘数法.

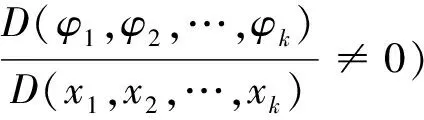
2.2 证法一

设点(x，y，z)是平面π：Ax+By+Cz+D=0上的任一点，则它与P(x0，y0，z0)的距离的平方

d2=(x-x0)2+(y-y0)2+(z-z0)2

(1)

问题转化为了求d2在约束条件Ax+By+Cz+D=0下的极大值.

令L(x，y，z，λ)=(x-x0)2+(y-y0)2+(z-z0)2+λ(Ax+By+Cz+D)，

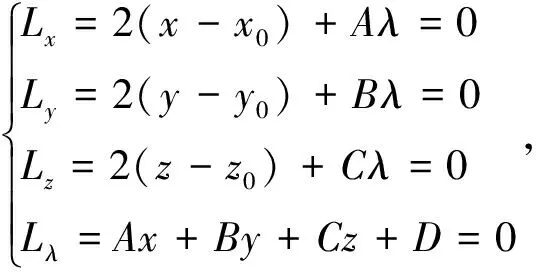
由于问题一定存在最小值，故所得驻点就是L的极小值点，将其带入式(1)中，得

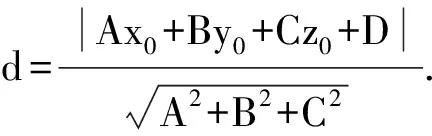
3 高等代数的角度

3.1 问题的表述与涉及的内容

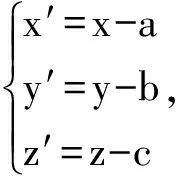
在解决这一问题前，先给出定理.

定理3[3](向量到子空间的距离) 设W是欧式空间V的一个子空间，对于V中的向量α，W中有向量α1是α在W上的正交投影的充分必要条件是|α-α1|≤|α-β|对所有的β∈W成立，称|α-α1|为向量α到子空间W的距离.

定理3说明，一个固定向量和一个子空间中各向量间的距离总是以“垂线最短”.

定理4[4](欧氏空间的几点性质)：

① 在n维欧氏空间V中，dimV1+dimV2=n；

② (α，kβ)=k(α，β)；

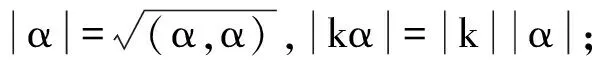
④ (α，β+γ)=(α，β)+(α，γ)；

⑤ V1⊥V2⟺∀α∈V1，∀β∈V2有(α，β)=0.

3.2 证法二

设α=(A，B，C)，则α∈W′⊥.

∵dimW′=2且R3=W′⊕W′⊥，∴dimW′⊥=1，∴W′⊥=L(α).

设ζ′在W′上的正交投影为η，由定理3知|ζ′-η|即为所求.

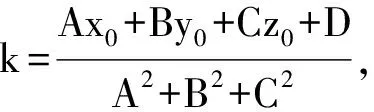
4 解析几何的角度

根据定理3，首先明确，过一点引平面的垂足，那么点与垂足间的距离即为点与与平面间的距离.接着，引入法式方程和离差的概念.

4.1 法式方程的概念

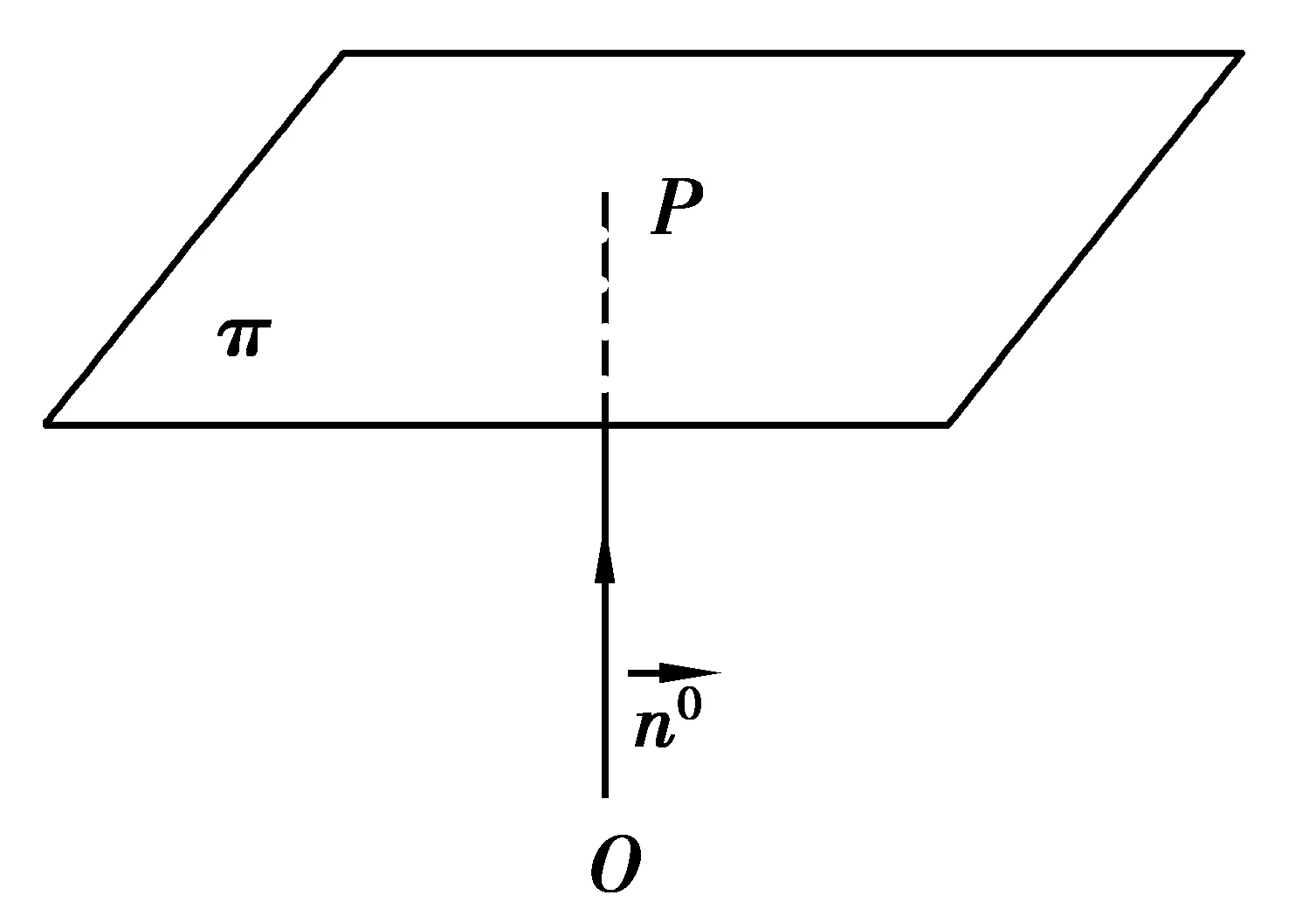
图1 “法式方程”示意图

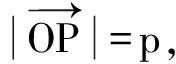
4.2 离差的概念及问题的表述

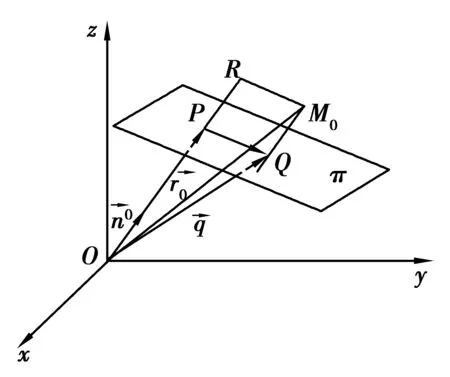
图2 “离差”示意图1

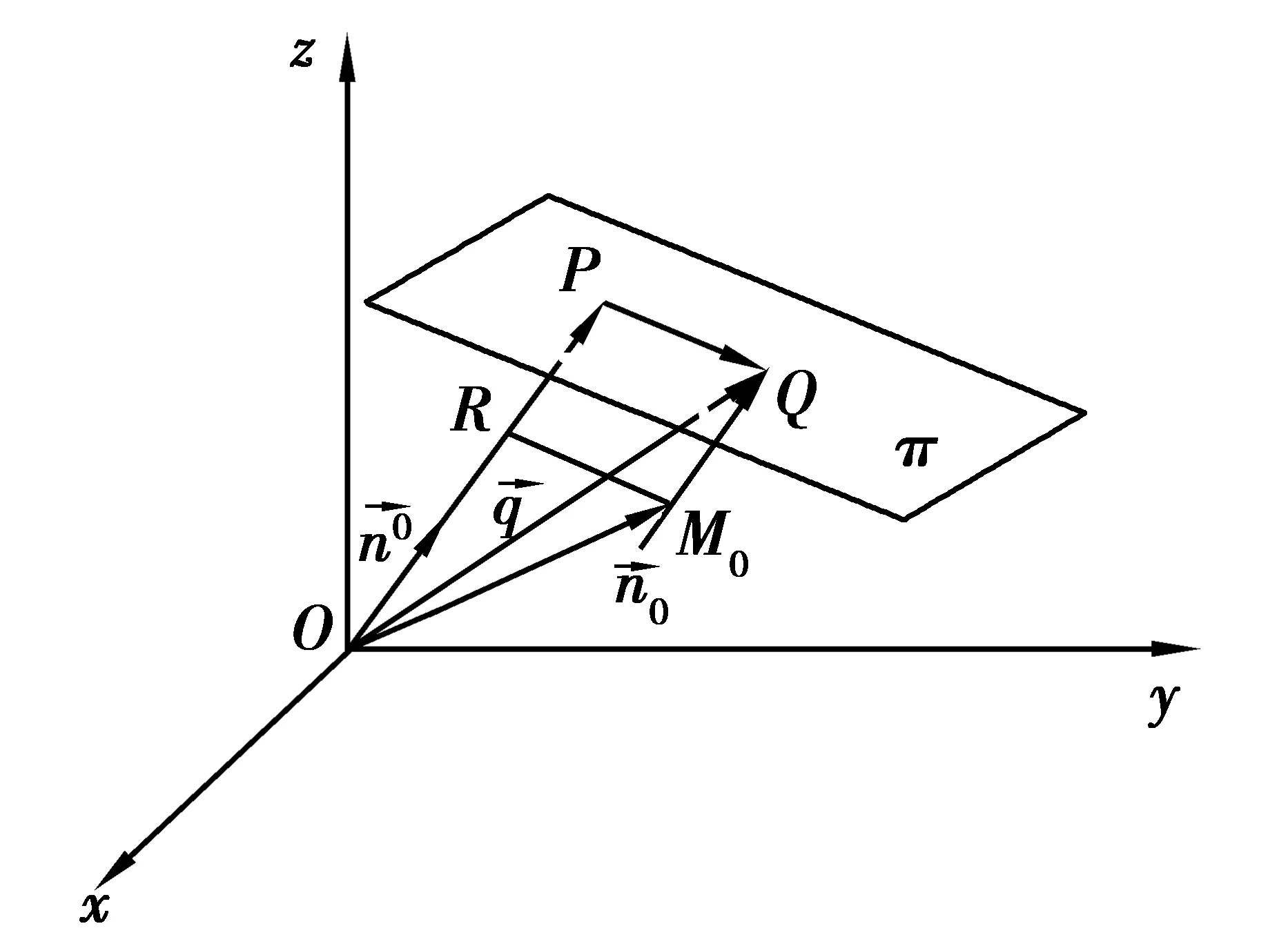
图3 “离差”示意图2

问题的表述3：从解析几何的角度，则点到平面的距离问题可表述为求M0与平面π间的离差δ的绝对值.

4.3 证法三

(1)

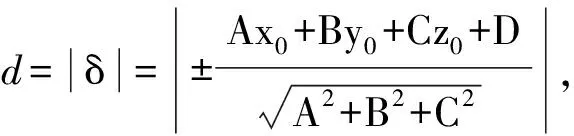
5 结 语

数学分析、高等代数和解析几何是大学数学类专业的3门主干基础课程，即通常所说的“三高”课程.数学分析研究的对象是函数，研究函数的性质、微分和积分等内容，它往往通过函数的模型解决问题.而高等代数所讨论的是代数系统，如多项式环、线性空间等，它的特点是概念的高度抽象性和定理的高度概括性.解析几何则是指借助坐标系用代数方法解决几何问题的学科.一般而言，高等代数与解析几何的关系显得较为紧密，他们本质是“数”与“形”的互动关系，高等代数中的理论可在解析几何中寻找模型，解析几何中的内容需依靠高等代数中的理论来解决.

事实上，虽然“三高”课程的理论和方法不同，处理问题的思想方法也不同，但他们也能相互联系，毕竟殊途同归.所举的关于点到平面的距离公式的3个证明便是一个典型的例子.再例如，最小二乘法公式的证明也可利用多元函数的极值及欧氏空间的距离分别加以证明.建议，在“三高”课程的学习过程中，应经常反思三者的联系渗透之处，找出相关的例子，并从三者不同的视角加以研究，以加深对其的理解.

参考文献：

[1] 吕林根.解析几何[M].第四版.北京：高等教育出版社，2006

[2] 欧阳光中.数学分析：下册[M].3版.北京：高等教育出版社，2007

[3] 易忠.高等代数与解析几何：下册[M].北京：清华大学出版社，2007

[4] 北京大学数学系几何与代数教研室前代数小组.高等代数[M].3版.北京：高等教育出版社，2003