高温气冷堆堆芯流场高效全局求解方法研究

周夏峰，李 富

(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室，北京 100084)

球床模块式高温气冷堆核电站示范工程(HTR-PM)已列入国家科技重大专项，其中HTR-PM堆芯流场的计算模拟是专项的重要部分之一。在高温气冷堆(HTGR)中，由于冷却剂氦气具有温度变化剧烈、密度变化大、流量分配上大流量和小流量并存，以及堆芯内流动区域相互耦合等特点，给HTGR的堆芯流场计算提出挑战[1]。目前用于HTGR的安全分析程序是THERMIX软件包，THERMIX系列程序中的KONVEK程序用于堆芯内流场的计算。考虑到堆芯内各部件的结构形式和流动特性，程序中设置了5种不同结构的流动区供用户选择，分别为不流动区、球床区、竖管一维流动区、换热器区及空腔区，不同区之间的流场相互耦合[2]。该软件包得到了德国GRS评审和我国核安全当局的认可，目前用于HTGR的安全分析[3]。

但由于程序编制年代较早，KONVEK程序采用了分块迭代方法计算相互耦合的全堆芯流场，即上述5种不同结构的流动区分别独立计算各自的流场，之后根据不同结构流动区之间的界面相互传递信息，不断迭代更新，直到收敛。分块迭代方法计算相互耦合的全堆芯流场时，部分工况收敛速度慢，耗时长，甚至会出现不收敛的问题。因此，本工作研究高效的全局求解方法计算HTGR堆芯流场分布。

1 数学物理模型

1.1 堆芯流场模型

HTGR一回路的冷却剂是氦气，由于氦气密度小，流动惯性力也非常小，因此它对流动条件的响应非常快，这意味着在每个短时间段都能调整到新平衡态，因此，在时间间距不太大时，可将堆芯流场按照准稳态处理，忽略时间相关项[4]。最终得到HTGR堆芯流场计算模型：

(1)

其中：Gr和Gz分别为质量流量G在r和z方向上的分量，G=ρu，ρ为气体密度，u为速度矢量；Φ为质量源项；W为流动阻力系数，也依赖于气体流速，W=W(G)，由经验关系式给出，堆芯内不同流动区的W不同；p为相对压力；g为重力加速度。

由式(1)可得压力Possion方程的计算关系式：

(2)

1.2 模型离散

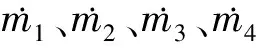
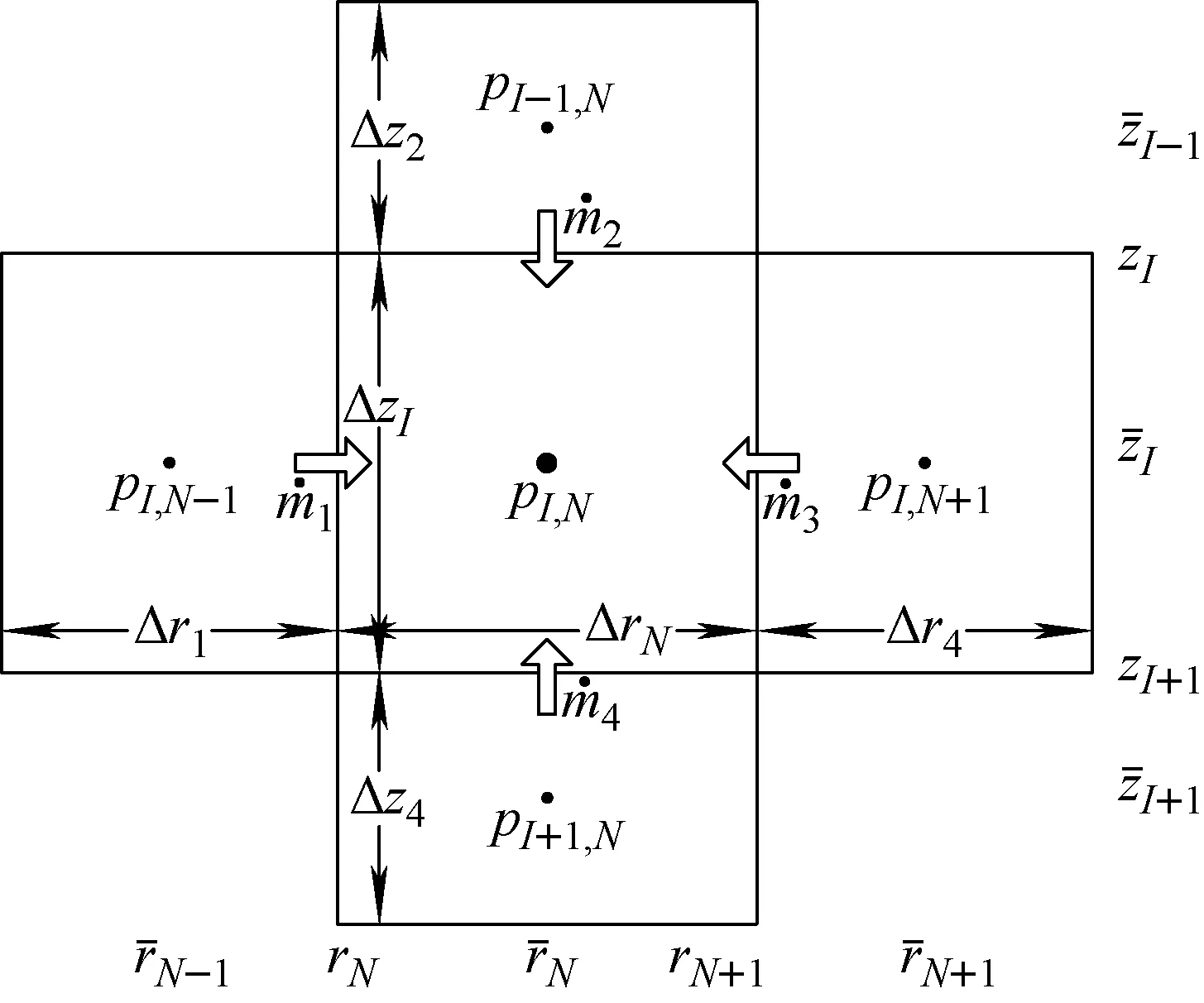
图1 压力控制容积的网格离散示意图

选取第(I，N)个网格，即压力控制容积，对式(2)中的压力场方程进行积分得：

A1(I,N)(pI,N-pI,N-1)+A2(I,N)(pI,N-

pI-1,N)+A3(I,N)(pI,N-pI,N+1)+

A4(I,N)(pI,N-pI+1,N)=ψI,N+

A2(I,N)ρI-1gΔzI-A4(I,N)ρIgΔzI+1

(3)

其中：

A3(I,N)=A1(I,N+1)

A4(I,N)=A2(I+1,N)

1.3 KONVEK程序中堆芯流场计算流程

式(3)中A1(I,N)、A2(I，N)、A3(I，N)含有阻力系数W，W为速度场的函数，因此堆芯流场的计算必然带有迭代性质。HTGR堆芯流场分布和耦合情况示于图2。由图2可知，HTGR堆芯内具有不同结构形式的流动区，各区的流场之间相互耦合，这使得在计算时需考虑耦合问题的求解方法。KONVEK程序采用分块迭代方法计算相互耦合的全堆芯流场，即不同结构流动区分别独立计算各自流场，之后根据不同结构流动区之间界面相互传递信息，不断迭代更新，直至收敛。流场计算流程如图3所示。

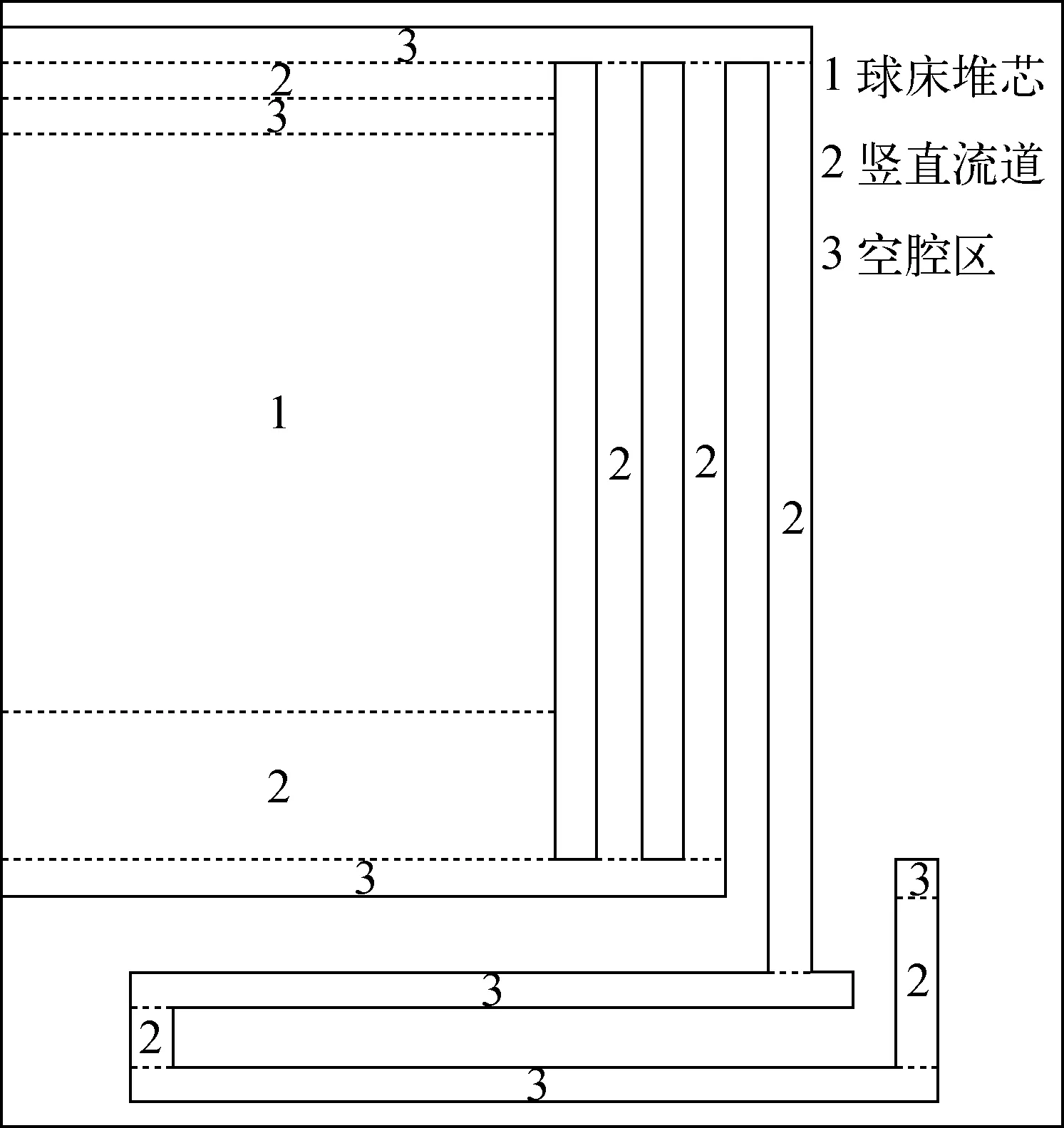
图2 HTGR堆芯流场分布和耦合情况

2 目前计算方法存在的问题

对于如图2所示的堆芯流场分布与耦合情况，堆芯中具有不流动区、球床区、竖直一维流动区和空腔区，各流动区之间通过边界相互耦合。依据堆芯不同结构的流动区，离散后的方程组写成以下形式：

(4)

其中：A为方程离散后形成的矩阵；X1为所有空腔区内各网格点压力所形成的向量；X2为所有球床区内各网格点压力所形成的向量；X3为所有竖直一维流动区内各网格点压力所形成的向量；向量b1、b2、b3分别为X1、X2、X3对应的已知源项。

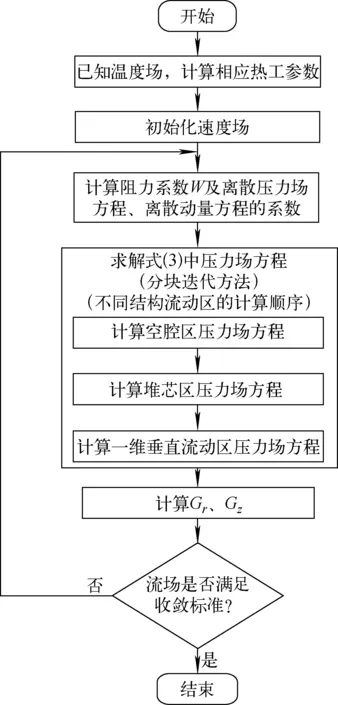
图3 KONVEK程序中堆芯流场计算流程

2.1 分块迭代方法存在的问题分析

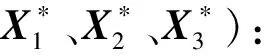
(5)

其中，n为迭代步。

对式(5)进行求解可得：

设G为：

为保持分块迭代的收敛性，需要使G的谱半径ρr(G)<1，且ρr(G)越小，收敛越快[6]，这与传统意义上的Gauss-Seidel迭代方法的原理相同，存在一定局限性。ρr(G)接近1或ρr(G)≥1时，会出现收敛慢，甚至不收敛的现象，计算时间会很长，从而影响计算精度。

2.2 压力场和流场计算方法存在的问题分析

由图3可知，在特定温度场下，首先根据上一步计算出的速度场得到压力方程的相关系数，之后利用分块迭代方法分别求解堆芯内不同结构流动区的压力场，之后得到各网格边界的压力梯度，再根据压力梯度计算网格边界的流量，更新速度场，反复进行上述过程，直到收敛为止。也就是说只要计算出压力场，速度场即可得到，由此可见，速度场的计算精度严重依赖于压力场的求解精度。

此外，压力场轻微变化将会引起堆芯内速度场的较大变化，所以压力场的收敛精度不够或不收敛时，会引起速度场始终有相当大的波动，最终导致速度场收敛较慢，甚至不收敛。

由2.1节分析可知：采用分块迭代方法处理相互耦合的堆芯流场，当分块迭代中迭代矩阵G的谱半径ρr(G)接近1或ρr(G)≥1时，会出现收敛慢，甚至不收敛的现象，这样就很难保证压力场的求解精度；由于KONVEK程序编制年代较早，在分别求解每一堆芯流动区的压力场时，使用了Gauss-Seidel迭代法来进行矩阵求解，部分工况计算时间较长，同样也很难保证计算的收敛性和计算精度。

综上所述，计算HTGR堆芯流场所使用的模型对压力场的求解精度需求很高，每次计算压力场时，需保证压力场计算方法的收敛性，并尽可能准确地求解压力场；分块迭代方法求解相互耦合的问题可能会出现收敛速度慢，甚至不收敛的问题，同时，选用Gauss-Seidel迭代法作为压力场的矩阵求解器，同样会出现上述问题。基于此，选取高效的全局求解方法处理堆芯相互耦合的问题，使用高效的直接求解方法求解压力场方程。

3 全局求解策略

分块迭代方法的本质是采用Jacobi或Gauss-Seidel方法求解式(4)，这样可能出现不收敛或收敛速度慢的问题，从而可能导致很难得到其收敛解。全局求解方法的本质则是将式(4)看作整体，联立求解。

由于直接消去法求解线性方程组时对谱半径和矩阵的条件数不敏感[7]，可得到高精度的数值解，即使对于较为病态的线性方程组，也能得到相对合理的解，同时直接消去法可实现压力场的全局求解。因此，为保证压力场计算的稳定性和准确性，避免谱半径对收敛性的影响，本文选取了选主元的高斯消去法作为堆芯流场计算的全局求解方法。

4 结果与分析

4.1 计算结果

为验证全局求解方法和程序编写的正确性，选取HTR-PM满功率稳态运行状态为计算对象，基本运行参数如下：满功率为250 MW；堆芯系统压力为7×106Pa；堆芯氦气入口温度为250 ℃；堆芯氦气入口流量为96 kg/s。分别用KONVEK程序和新开发的全局求解程序对选取的问题进行计算，图4示出计算的堆芯压力场分布情况。由图4可见：新开发的全局求解程序计算出的压力场分布与KONVEK程序计算结果吻合很好，只有极少数的网格点出现0.1%～0.5%的相对误差，这是由于这些地方的相对压力很小，几乎接近零的缘故。

a——KONVEK程序；b——新开发的程序；c——计算结果的相对误差

4.2 计算效率

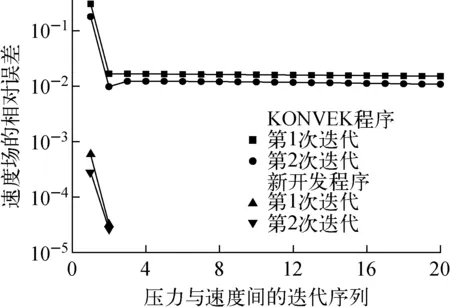
图5 收敛特性对比

为能够充分体现全局求解方法的计算效率，选取HTR-PM瞬态运行状态作为计算对象，基本运行参数如下：堆芯系统压力为7×106Pa；堆芯氦气入口温度为250 ℃(恒定)；堆芯氦气入口流量在0～1 h时为96 kg/s，1～1.5 h时从96 kg/s线性降至0.01 kg/s，1.5～3 h时保持0.01 kg/s不变。通过对比KONVEK程序和新开发的全局求解程序的收敛特性和计算时间，来分析新开发程序的计算效率。图5示出HTR-PM瞬态运行过程中1.407 h工况时间段内流场的收敛特性曲线。在该工况时间段内，温度场与流场之间迭代了2次，每次流场计算的收敛特性如图5所示。由图5可知：当速度场的收敛精度达到0.01附近后，速度场收敛很缓慢，几乎不收敛，很难达到更高的精度；而新开发的程序仅需要2步迭代，速度场的收敛精度就可达到5×10-5。新开发的程序在收敛速率上有明显优势。

将新开发的全局求解模块应用于THERMIX程序包，分析全局求解方法对堆芯流场和温度场总计算效率的影响，表1列出堆芯流场和温度场的最终收敛情况。由表1可知：原THERMIX程序包在计算流场时收敛速度慢，压力场与速度场之间迭代900次仍不收敛，从而导致温度场和流场之间迭代100次也不收敛，在表1所列每个工况时间段的计算效率均相对较低，耗时长；新开发的全局求解程序大幅提高了计算效率，流场和温度场均在最大迭代次数之前很快达到收敛标准，计算效率提高了几十倍，甚至上百倍，说明了该全局求解方法的高效性。

5 总结

对分块迭代方法的收敛性分析研究表明：当分块迭代中迭代矩阵G的谱半径ρr(G)接近1或ρr(G)≥1时，就会出现收敛慢，甚至不收敛的现象，并难以保证压力场的求解精度。本文开发了适用于计算HTGR堆芯流场的高效全局求解方法，并对HTR-PM稳态和瞬态运行状态进行了验证计算，与分块迭代方法相比，高效全局求解方法的收敛性和计算效率均有很大提高。

表1 计算效率对比

参考文献：

[1] 吴宗鑫，张作义. 先进核能系统和高温气冷堆[M]. 北京：清华大学出版社，2004：238-245.

[2] CLEVELAND J C, GREENE S R. Application of the THERMIX-KONVEK code to accident analyses of modular pebble bed high temperature reactors[R]. USA: Oak Ridge National Laboratory, 1986.

[3] 清华大学核能与新能源技术研究院. 华能山东石岛湾核电厂高温气冷堆核电站示范工程初步安全分析报告[R]. 北京：清华大学核能与新能源技术研究院，2008.

[4] 王登营. 高温气冷堆多回路系统的模拟[D]. 北京：清华大学核能与新能源技术研究院，2011.

[5] 陶文铨. 数值传热学[M]. 2版. 西安：西安交通大学出版社，2001：198-203.

[6] HOOPER R, HOPKINS M, PAWLOWSKI R, et al. Final report on LDRD project: Coupling strategies for multi-physics applications, SAND2007-7146[R]. USA: Sandia National Laboratories, 2007.

[7] 关治，陆金甫. 数值分析基础[M]. 2版. 北京：高等教育出版社，2010：35-66.