三种模型级联的比较

张宇楠，曾 实

(清华大学 工程物理系，北京 100084)

同位素在生产与科研中的应用日益广泛，各种同位素的需求量也迅速增长，尤其是利用目前最大规模和最经济的分离铀同位素的离心法分离非铀的稳定同位素，推动了多组分同位素分离级联的研究。相对于理论已相当成熟的双组分分离级联(特别是铀浓缩级联)研究，多组分分离级联这一领域还有很多亟待解决的问题，如在传统的级联形式中无法实现各级之间的交汇点处各组分丰度无混合，难以合理确定各级之间最合适的连接条件；在多组分分离中未能得到公认的价值函数定义，难以利用价值函数和分离功率的概念分析和评价级联的分离性能；一般形式的多组分分离级联的计算牵涉到求解非线性方程组[1]，不方便进行一般性的分析和研究。此外，在涉及生产实际时，由于对稳定同位素的需求在量、种类、丰度方面的要求均不同，需建立不同的分离级联并采用不同的运行方式，而这成本高昂、费时长。故以真实实验的方式研究各种多组分分离不现实。

为解决这些问题，探索高效分离多组分同位素的方法，提出了模型级联的概念。这些模型级联是对一般形式的多组分分离级联提出一些特殊的限制条件后得到的，它们通常具有相对简单的形式，易于计算，又能反映多组分分离级联的一般规律和特性，因此可作为解析或数值分析级联性质的合适对象。模型级联的一典型例子即双组分分离的理想级联，在大规模的铀同位素分离实践中得到检验，目前仍在指导生产实际中发挥重要作用。然而，对于多组分分离，提出不同的要求可得到不同的模型级联，如要求交汇点处来流中某两组分的丰度比相等，则得到相对丰度匹配级联[2](matched abundance ratio cascade，MARC)；要求各级的组分分流比相等则构造出准理想级联[3]；而采用小分离系数、连续流量的假设则构造出Q级联[4-5]。

模型级联无论对于实际级联设计还是分离理论的研究均有重要作用。就前者而言，模型级联可为实际级联设计提供一参考。如Kolokol′tsov等[5]提出可用优化后的Q级联为模板，设计阶梯级联逼近Q级联的形状；宋天明等[6]通过优化MARC分离Si同位素，证实其结果非常接近于直接优化得到的最优解，适合指导实际级联的设计。事实上，直接对多组分分离级联进行优化设计，计算量很大，耗时很长，通常选择相对易计算的模型级联给出一结果，再以此结果为初值或目标，考虑各实际因素后，进一步简化和优化得到所需的实际设计方案，或分析实际情况中的缺陷。此外，模型级联是分离理论研究的重要工具。如谢全新等[7]以准理想级联为模型，研究了存在多个供取料、有物料损失的级联分离行为；Zeng等[8]也以Q级联为模型进行过类似的研究。实际上，无论是理想级联、相对丰度匹配级联，还是准理想级联或Q级联，人们一直在努力探索最优的分离级联，以及最优分离的物理本质。鉴于理想级联在指导铀同位素分离的成功，模型级联无论从理论和实验上均成为了同位素分离研究中的重要对象。

本文针对最常使用的三种模型级联，即Q级联、MARC级联、准理想级联进行分析，并对它们的背景以及关键参数、基本的分离特性等进行总结介绍。以往的研究均发现这几种模型级联之间存在很大的相似性和联系[1，9-10]，但不够明确。本文拟通过较全面和系统的对比分析更明确地揭示其内在的联系，进一步认识这些级联的本质，使对三种模型分别的研究工作能在一定程度上统一起来，避免或减少不必要的分析。

1 三种模型级联

为在相同的条件下进行对比研究，本文以传统的双管道逆流级联结构为研究对象。在级联的两端分别获得精料流量P和贫料流量W，在中间某级引入供料流量F，如图1所示。

图1 连续流量级联结构(a)和离散流量级联结构(b)

1.1 Q级联

Q级联是一种连续流量的模型级联(model cascade of continuous profile，MCCP)，它是从MCCP的一般模型出发，通过给定一组特征函数φi(l)的特殊形式得到的[4]。Q级联的级数为实数，流量是级数的连续函数，因此称其为连续流量级联。MCCP的提出是为在弱分离的情况下，通过适当简化，将多组分分离级联离散形式的级间物质输运关系转化为微分形式，设法求解微分方程得到级联连续形式的近似解。

假如引入一组特征函数φi(l)取代各组分的丰度Ci(l)，通过一些数学手段可将微分输运方程改写成如下积分形式[5，11]：

贫化段

浓化段

(1)

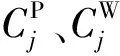
对φi(l)的要求为：

(2)

为导出Q级联，令：

(3)

其中，流量Q满足：

Qi-Qj=εij

(4)

在此条件下，式(1)具有特别简单的形式，可得到：

i=1,2,…,NC

(5)

其中，SW、SP分别为Q级联贫化段和浓缩段的长度。

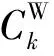
对于离心分离、扩散分离，单级的分离系数满足如下关系：

(6)

其中：γ0为单位摩尔质量差的全分离系数；M为分子量。考虑相对浓缩系数εij：

εij=lnγij=ε0(Mj-Mi)

(7)

其中，ε0=lnγ0为单位摩尔质量差的浓缩系数，可作为衡量分离强弱的标准。

Q通常是人为给定的，因此，设：

Qi=ε0(M*-Mi)

(8)

其中，M*为虚拟组分分子量，数值给定。根据式(4)，有：

Qi∝ε0

(9)

由式(5)可知，决定Q级联取料丰度的是QiSW和QiSP，若随着ε0的变化，Q级联的长度SW和SP也相应变化而使ε0SW和ε0SP不变，则级联的各组分取料丰度就不会变化。对于Q级联的流量分布也有类似的结论。

因此，ε0SW、ε0SP相等的Q级联均可视为相似的，具有相似的丰度和流量分布，这也说明Q级联模型不限于ε0远小于1的弱分离情况。

由于Q级联计算简单，易于分析，为多组分分离级联研究中最广泛使用的模型之一，文献[12-13]以Q级联为模型讨论了多组分分离级联内中间质量组分的丰度分布规律与分离策略；文献[11，14]则讨论了Q级联的优化设计问题。

1.2 MARC级联

寻找实用的多组分同位素混合物的价值函数和分离功率的形式一直是研究的重点，众多学者也提出了多种不同的价值函数定义形式，但均存在各自的问题而无法得到普遍的认可。文献[2]试图通过考察三种组分分离的特殊情况，结合对价值函数一些实用性的要求得到适用于多组分混合物的价值函数定义：设想对于不同丰度组成的多组分混合物，定义一匹配函数，当混合物的匹配函数值相等时，两种混合物可任意混合而不产生总价值的变化。从这样的思想出发，并借助一些数学上的推演，de la Garza等[2]得到了匹配函数与价值函数的关系，并给出了它们必须满足的限制条件，当选取关键组分的相对丰度R作匹配函数值时，得到了三组分情况下各级之间不因混合而产生价值损失的级联形式。由于是以相对丰度作为匹配标准，因此称为相对丰度匹配级联，即MARC。后来又将MARC的概念和相应的价值函数与分离功率定义推广到更多组分的情况下[15]。

要确定一MARC的形式，必须事先定义两种组分：关键组分，记为组分k；参考组分，记为组分n。在MARC的各级之间，要求匹配这两种组分的相对丰度，即：

(10)

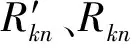
由于每个分离级的分离特性要求：

(11)

其中，αkn为两种组分的浓化系数。结合式(10)，可知：

(12)

即MARC中的关键组分相对于参考组分是对称分离的。根据式(10)、(12)以及各级质量守恒：

(13)

可得式(14)[15]：

(14)

1.3 准理想级联

准理想级联是文献[3]提出的，指各分离级的组分分流比φi为常数的离散级联。

组分分流比的定义为：

(15)

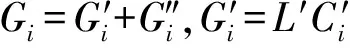
(16)

显然，βi=φi/(1-φi)，准理想级联的组分分流因子也保持为常数。

引入组分分流因子的概念可使多组分分离级联的计算在形式上相对容易[17]，准理想级联的物质输运关系可简化为：

(17)

(18)

(19)

其中，δsNf为Kronecker符号。

当然，与Q级联中的Qi相同，各组分的βi也不是任意的，必须满足一定的约束关系。实际上，只要给定某组分(如关键组分)的组分分流因子，根据1个分离级的分离特性，可直接确定其余各组分的βi：

βi=γikβk

(20)

其中，k为关键组分的编号。应注意，这一关系不仅限于准理想级联。

对式(17)、(18)、(19)的求解结果为：

(21)

准理想级联由于计算简单，也广泛应用于多组分分离研究中。

2 三种模型级联之间的联系

首先要指出的是，式(5)、(14)、(21)在形式上明显类似或完全相同，说明三种级联之间可能有深层的联系。

以往的研究也涉及对三种模型之间的关系分析。文献[1]从Q级联出发，得到了两种组分相对丰度匹配的条件，指出由此可将Q级联得到的组分丰度分布、总流量等结论应用于MARC。文献[9]尝试利用弱分离近似，证明Q级联的组分分流比φi与准理想级联的均为常数，从而将二者归为一类，但其推导方法在级联长度较长的情况下并不合适，仍有待商榷。文献[10]引入组分分流因子的概念简化三组分MARC的计算，但当时尚未有准理想级联的概念，且也未进一步推广到更多组分的情况。

本文将在以往研究的基础上，分析总结三种模型级联之间的相似处以及相互关系，更系统地建立三者之间的联系。

2.1 准理想级联与MARC

根据式(12)，MARC的任一级对于k、n两组分均是对称分离的，即：

(22)

根据组分分流因子的定义，有：

(23)

将式(23)代入式(22)，可得：

(24)

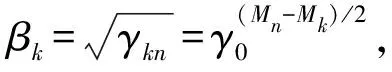
从另一角度看，对于准理想级联，根据式(20)，指定关键组分的βk，其余的组分分流因子就都确定了，由于只要求βk>0，因此，可令：

(25)

其他组分的组分分流因子可写成：

(26)

因此，所有组分分流因子均可由M*确定。

对于MARC，由式(24)可知：M*=(Mk+Mn)/2。因此，MARC只是准理想级联的虚拟组分分子量取特定值时的一种特例。具体来说，M*取两种组分分子量的算术平均值时，这两种组分在各级之间满足相对丰度匹配的条件，准理想级联就成为了一MARC。

2.2 准理想级联与Q级联

准理想级联与Q级联的相似之处可非常明显地从式(5)、(21)中看到。假如作如下对应：

SW→Nf，SP→N-Nf+1，βi→eQi

(27)

则两种模型级联的取料丰度的表达式完全一致。

进一步可证明在一定近似下，Q级联也同准理想级联一样，具有常数的组分分流因子。以贫化段为例，在相邻两级之间，根据物质输运关系，可得：

(28)

利用

(29)

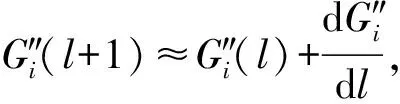
(30)

另外，从Q级联的积分输运方程(式(1))出发，可得到：

(31)

利用边界条件

(32)

可求解式(30)，得到：

(33)

进而可得：

(34)

一般，ε0≪1，而Mi与M*相差不大，故|Qi|≪1，由式(34)近似可得：

(35)

由式(29)、(31)、(35)，可知：

(36)

这说明在近似情况下，Q级联的各组分分流因子恒定为常数，与准理想级联相同。

另外，在Q级联中，同样可引入类似于准理想级联的虚拟组分分子量M*。根据式(4)，考虑εij的定义，可知：

Qi-Qj=ε0(Mj-Mi)

(37)

根据式(8)，式(37)一定得到满足。

M*对Q级联和准理想级联均为重要的控制参数，其取值影响级联的特性，因此，对Q级联或准理想级联的优化是针对M*进行的。但本文重点是比较研究不同的级联，优化设计流程以及对M*参数范围的设置可参考文献[12，14]。从物理意义看，M*的取值决定了级联对不同质量组分的分离特性，这在文献中有分析，但由于其非常重要，在下面对此稍加解释。

在Q级联中，对于轻组分，Qi>0，根据式(36)，βi>1；而对于重组分，βi<1，这也与准理想级联的规律一致。归纳起来，在准理想级联或Q级联中，轻组分经一个分离级后会更多地流向轻端，而重组分则相反，表明M*将所有组分划为轻、重两类，轻组分向着精料端被浓缩，而重组分向着贫料端被浓缩。但在精、贫料端获得同样的目标组分丰度下，M*的取值影响级联的总流量(各级入口流量之和)。为取得最好分离效益，希望用最小的总流量取得同样的分离效果，这样，M*就成为一优化的参数，用来对MARC级联[18]、准理想级联[19]或Q级联优化[11]。

Q级联是一连续级联，而准理想级联却是离散的，二者之间不是严格的对等关系，但已可确定这两种模型级联具有相似的特性，可视为同一类级联模型。

当然，上面的分析也完全适用于描述Q级联和MARC级联之间的关系。

3 小结

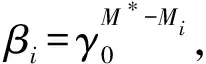
虽然Q级联是一连续级联，无法与准理想级联完全等同，但分析可知，两种级联均可引入虚拟组分分子量M*，且其对于级联的分离特性有相同的影响作用。更重要的是，与准理想级联类似，Q级联的组分分流比在近似条件下可视为常数。认为Q级联和准理想级联是相似的级联模型是合理的。

因此，可将这三种模型级联归为一种级联，根据实际情况针对一种级联进行研究。

参考文献：

[1] SULABERIDZE G A, BORISEVICH V D. Cascades for separation of multicomponent isotope mixtures[J]. Separation Science and Technology, 2001, 36(8-9): 1 769-1 817.

[2] de la GARZA A, GARRETT G A, MURPHY J E. Multicomponent isotope separation in cascades[J]. Chemical Engineering Science, 1961, 15(3): 188-209.

[3] SAZYKIN A A. Quasi-ideal cascades for separation of multicomponent isotope mixtures[C]∥Proceedings of 5th Scientific Conference on Physicochemical Processes in Selection of Atoms and Molecules. Zvenigorod, Russia: [s.n], 2000: 51-57.

[4] KUCHEROV R Y, MINENKO V P. Theory of cascades for separating multi-component isotope mixtures[J]. Soviet Atomic Energy, 1965, 19(4): 1 290-1 300.

[5] KOLOKOL′TSOV N A, MINENKO V P, NIKOLAEV B I, et al. Design of cascades for separating isotope mixtures[J]. Soviet Atomic Energy, 1970, 29(6): 1 193-1 198.

[6] 宋天明，曾实. 多组分气体离心分离级联的解析优化[J]. 清华大学学报：自然科学版，2006，46(12)：2 003-2 006.

SONG Tianming, ZENG Shi. Optimization of centrifuge cascades for the separation of multi-component gas mixtures[J]. Journal of Tsinghua University: Science and Technology, 2006, 46(12): 2 003-2 006(in Chinese).

[7] 谢全新，丛艺坤，邱志恒，等. 带附加供料流和存在损耗的准理想级联模型[J]. 同位素，2013，26(3)：180-185.

XIE Quanxin, CONG Yikun, QIU Zhiheng, et al. Model of quasi-ideal cascade with an additional feed flow and losses of working substances[J]. Journal of Isotopes, 2013, 26(3): 180-185(in Chinese).

[8] ZENG S, SMIRNOV A Y, JIANG D, et al. Isotopically selective mass transfer in the Q-cascade with losses of working substance[J]. Separation Science and Technology, 2013, 48(1): 15-21.

[9] ZENG S, SULABERIDZE G A, JIANG D, et al. The Q-cascade explanation[J]. Separation Science and Technology, 2012, 47(11): 1 591-1 595.

[10] YAMAMOTO I, KABA A, KANAGAWA A. Simple formulae for analyzing matched abundance ratio cascade with constant separation factors for multi-component isotope separation[J]. Journal of Nuclear Science and Technology, 1987, 24(11): 969-971.

[11] BORISEVICH V D, SULABERIDZE G A, ZENG S. New approach to optimize Q-cascades[J]. Chemical Engineering Science, 2011, 66(3): 393-396.

[12] ZENG S, YING C. A method of separating a middle component in multicomponent isotope mixtures by gas centrifuge cascades[J]. Separation Science and Technology, 2000, 35(14): 2 173-2 186.

[13] SMIRNOV A Y, SULABERIDZE G A, BORISEVICH V D. Influence of feed flow profile of cascade stages on the mass transfer of intermediate components[J]. Theoretical Foundations of Chemical Engineering, 2011, 44(6): 888-896.

[14] ZENG S, JIANG D, BORISEVICH V, et al. Use of the Q-cascade in calculation and optimization of multi-isotope separation[J]. Chemical Engineering Science, 2011, 66(13): 2 997-3 002.

[15] WOOD H G, BORISEVICH V D, SULABERIDZE G A. On a criterion efficiency for multi-isotope mixtures separation[J]. Separation Science and Technology, 1999, 34(3): 343-357.

[16] SULABERIDZE G A, BORISEVICH V D, XIE Q. Quasi-ideal cascades with an additional flow for separation of multicomponent isotope mixtures[J]. Theoretical Foundations of Chemical Engineering, 2006, 40(1): 5-13.

[17] YAMAMOTO I, KANAGAWA A. Multicomponent isotope separating cascade composed of elements with large separation factors[J]. Journal of Nuclear Science and Technology, 1978, 15(8): 580-584.

[18] von HALLE E. Multicomponent isotope separation in matched abundance ratio cascades composed of stages with large separation factors[C]∥Proceedings of 1st Workshop on Separation Phenomena in Liquids and Gases. Darmstadt, Germany: [s. n.], 1987: 325-356.

[19] SULABERIDZE G A, XIE Q, BORISEVICH V D. On some properties of quasi-ideal cascades with losses at stages[J]. Ars Separatoria Acta, 2006, 4: 467-477.