RFQ冷却聚束器束流冷却后的性质模拟

朱志超，黄文学，罗 文，周青芝，宋英明,*，王 玥，田玉林，王均英，孙宇梁

(1.南华大学 核科学技术学院，湖南 衡阳 421001；

2.中国科学院 近代物理研究所，甘肃 兰州 730000)

缓冲气体冷却束流被广泛运用于各种核谱仪设备中，如ISOLTRAP[1]、HIPTRAP[2]、JYFLTRAP[3]、LEBIT[4]、CPT[5]、LPT[6]等。为克服束流的横向发射度和纵向能量分散较大的缺点，满足高精度测量的需要，国外一些大型实验室采用在放射性束流线后增加一个旨在降低束流发射度和能量分散的RFQ冷却聚束器，以高效率地收集和冷却经充气反冲质量分离器分离后的次级束流，使其具有非常小的发射度和能量分散，并把冷却后的高品质束流传输至后续设备，为离子的进一步操纵、精细的核结构和核衰变研究及高精度的质量测量提供条件。目前，中国以超重核的合成和衰变性质研究为主的超重核研究谱仪(SHANS)正在建造中[7]。其中RFQ冷却聚束器RFQ1L是SHANS的一关键设备。

束流在RFQ冷却聚束器中的冷却和约束及整个传输过程非常复杂，束流包络及束流性质受到各种参数的影响，因此，得出束流在RFQ冷却聚束器中的运动规律十分重要。RFQ冷却聚束器中的束流完全冷却后的性质与RFQ冷却聚束器调试参数之间的关系，目前少有文献提及。本文拟采用国际上较先进的真实相互作用势(RIP)模型，利用蒙特卡罗方法模拟束流在RFQ冷却聚束器中的运动，得出束流完全冷却后的性质与RFQ冷却聚束器的调试参数之间的关系，为RFQ冷却聚束器的研制提供参考。

1 RFQ冷却聚束器基本工作原理

提供射频(RF)四极电场的典型RFQ冷却聚束器双曲面电极如图1所示。4个双曲面电极对称装配，并在相邻电极加上幅度相同、频率相同、而相位相差180o的射频正弦波信号，从而产生约束束流的RF四极电场。入射束流沿z轴正方向。

离子在RF四极电场中的运动方程称为Mathieu微分方程。标准的Mathieu微分方程为：

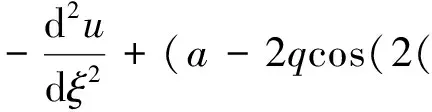
(1)

其中：ξ为相位；ξ0为离子刚开始受到电场作用时的RF四极电场的相位，即初始相位；u代表x或y，离子在x或y方向的横向速度即为du/dξ。

Mathieu微分方程参数为：

(2)

(3)

其中：r0为RFQ冷却聚束器特征半径；U为施加在双曲面电极上的直流电压幅度；V为加在双曲面电极上的RF电压值；ω为RF四极电场角频率(ω=2πf，f为RF四极电场频率)；e为离子的电荷。

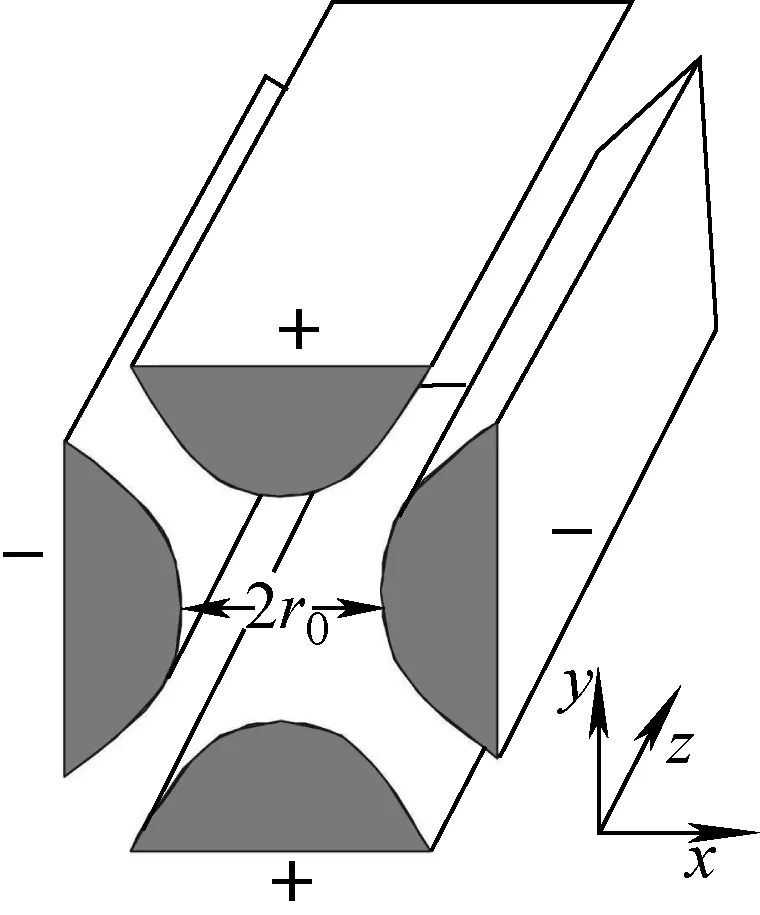
图1 提供RF四极电场的RFQ冷却聚束器的双曲面电极

当RFQ冷却聚束器收集和冷却所有类型的离子时，则不在双曲面电极上施加直流电压(a=0)，从而不对离子进行选择，形成一离子收集系统。研究表明，当q<0.908时，离子运动稳定[8-9]。

Mathieu微分方程稳定运动的通解[9]为：

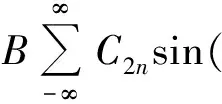
(4)

其中：A和B为常数，取决于离子的初始位置、初始速度和初始相位；C2n与a和q值有关；β与离子的运动频率相关。

由式(4)可知，离子的稳定运动其实是一系列正弦和余弦运动的叠加。当n=0时，即u(ξ)中的第一项，称为宏运动。n=1时的运动称为微运动或RF运动，n=2及更高阶的运动常被忽略。

当q<0.908时，宏运动振幅较微运动的大得多，可近似将总的离子运动视为宏运动，此时离子周而复始地绕RFQ冷却聚束器束流轴线做近似简谐运动，此即离子的约束；当离子与缓冲气体分子发生碰撞，离子的动能将逐渐降低且运动幅度减小，最终与缓冲气体分子达到热力学平衡，此即离子的冷却。

图2为RFQ冷却聚束器整体工作示意图。入射束流经过减速器降能，进入RFQ冷却聚束器，此时束流的发射度和能量分散均很大。在RF四极电场的约束和缓冲气体的降能下，离子的动能将逐渐降低，最后被冷却且被约束于RFQ冷却聚束器中心轴线附近。为引导离子到达引出系统，一般采用分段的轴向电极，在不同段电极之间施加不同的电位以产生轴向电场。

图2 RFQ冷却聚束器整体工作示意图

2 模拟模型

离子与气体分子发生每次碰撞，其相位就发生变化，动能和运动方向也发生变化，且离子与气体分子何时发生下次碰撞不可精确预知，所以离子的具体运动不可能通过解析计算得到，必须通过模拟来计算。目前国际上常用的模拟模型为：黏滞阻力(VDF)模型、硬球碰撞(HSC)模型和RIP模型。VDF模型是一种宏观模型，通过时间平均的作用力来描述缓冲气体对离子的冷却，而HSC模型和RIP模型是微观模型，通过蒙特卡罗方法逐个跟踪离子与缓冲气体分子的碰撞来模拟冷却的整个过程，并记录每个时间步长离子的信息，如速度矢量、加速度、位置、时间等。

VDF模型可很好地预测离子的冷却时间，结合离子能损，可用其来估计RFQ冷却聚束器所要求的尺寸大小，但由于未考虑离子与气体分子的碰撞，故该模型得不到束流冷却后的统计性质，且该模型会过高地估计离子冷却过程的有效性[10-11]。HSC模型把离子与气体分子之间的碰撞看作两个硬球之间的弹性碰撞，离子穿过中性的缓冲气体，与之碰撞并发生弹性散射。HSC模型虽可模拟碰撞的基本性质，但不能给出精确的量的预测，如不能准确预测散射角、标准迁移率等[12-13]。RIP模型中采用的两体相互作用势接近离子与气体分子之间真实的作用势，故该模型能给出精确的量的预测，即能准确预测散射角、散射截面、冷却离子的分布和平均动能等[13-15]。RIP模型的迁移率与实验数据较吻合[16-17]，能量适用范围较其他模型广[18]，目前在缓冲气体冷却领域是非常精准的一种模型。因此，本文选用RIP模型。

RIP模型中离子与气体分子之间的相互作用势[13,15]为：

(5)

其中：r为离子和气体分子之间的距离；C4/r4和C6/r6分别为离子电荷与其引起的电二极矩及电四极矩之间的吸引力作用；B/rn为短程的排斥力作用。此作用势又称(n，6，4)相互作用势。

离子与气体分子相互作用后的散射角可根据碰撞参数b和质心系动能E计算：

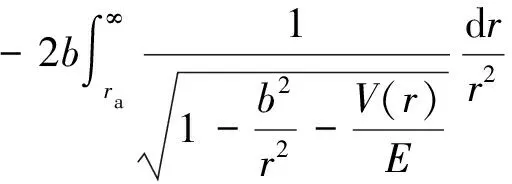
(6)

其中：ra为离子和气体分子碰撞期间最接近的距离，是式(7)的最大根。

(7)

离子与气体分子间相互作用势和碰撞截面之间可通过一系列积分联系起来。碰撞截面Ω(一级近似)可表示为温度的函数：

(8)

其中：Teff为有效温度；kB为玻尔兹曼常数，kB=1.38×10-23J/K。

将离子分子碰撞中的速度用Teff来表示，有：

(9)

其中：Tgas为气体温度；m为离子的质量；vd为离子的速度。

离子迁移率K与Ω(Teff)之间的关系[15]为：

(10)

其中：Q为离子电荷；N为气体分子密度；M为气体分子的质量。

通过上述公式，可将V(r)和Ω(Teff)联系起来，并可通过Ω(Teff)来计算离子迁移率。

3 模拟结果

本文采用RIP模型，结合IonCool程序包[13-14]和SIMION软件对束流在缓冲气体中的运动进行了详细模拟，得出束流完全冷却后的性质与RFQ冷却聚束器的调试参数之间的关系。以下所有模拟基于RFQ1L的几何参数：RFQ冷却聚束器特征半径60 mm；RFQ冷却聚束器约束冷却段长度1 600 mm。

3.1 单个离子模拟结果

为了解离子在RFQ冷却聚束器中的运动性质，模拟了单个离子在RFQ冷却聚束器中的运动。图3为RIP模型模拟得到的单个40Ar+离子在2.5 Pa 的He缓冲气体中的典型运动轨迹(入射沿束流轴线z轴正方向，初始能量为1 keV，q为0.5，RF四极电场频率为500 kHz，T=300 K，无轴向电场)。可看出，初始动能为1 keV的40Ar+离子在RF四极电场的作用下做Mathieu运动，并不断与缓冲气体分子发生碰撞，40Ar+离子的动能逐渐降低，其最终被冷却和约束在束流轴线z轴上。冷却后的40Ar+离子，继续受缓冲气体的碰撞和RF四极电场的约束，长时间在z轴1 400 mm处附近做随机的热力学运动。

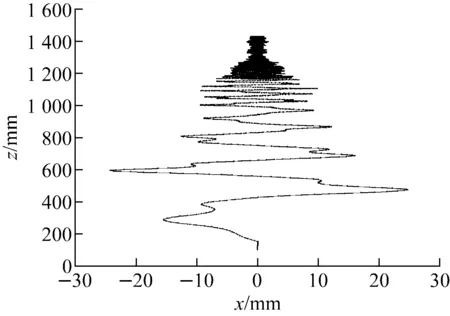
图3 单个40Ar+离子在He缓冲气体中的运动轨迹

图4a、b分别为RIP模型模拟得到的40Ar+离子的运动幅度及能量随时间的变化。为与RIP模型作对比，图4c、d分别示出在相同条件下，采用VDF模型模拟得到的该离子的运动幅度及能量随时间的变化。从图4c可看出，在VDF模型下，运动幅度将持续减少直至接近零，显然是不符合实际的。从图4d可看出，在VDF模型下，40Ar+离子能一直被缓冲气体冷却，其能量已降低至10-9eV附近，这也与实际不符。因此，VDF模型不能正确模拟被缓冲气体冷却后的束流性质。

从图4a可看出，RIP模型下，在0～300 μs时间内40Ar+离子的运动幅度逐渐下降，在300 μs左右下降至最低，在300～2 000 μs时间内，运动幅度并未随时间变化而变化。本次模拟运行时间为2 000 μs，实际上运行时间达1 min或更长，运动幅度并不会更小。

从图4b可看出，40Ar+离子的初始能量为1 keV，经过与缓冲气体的碰撞，在0～300 μs时间内能量急剧下降，在300～2 000 μs时间内40Ar+离子的动能一直保持平衡，在0.04 eV(300 K时He气的平均热力学动能)附近振荡。

通过图4a、b可认为，40Ar+离子的冷却时间约为300 μs，40Ar+离子在冷却后运动幅度保持平衡，平均动能保持与缓冲气体的热力学平衡。

由图4a、b可知，40Ar+束流在完全冷却后，束斑将保持一定，不随时间变化而变化；能量分散与缓冲气体将保持热力学平衡，亦不随时间变化而变化。

3.2 多个离子模拟结果

在本节的所有模拟中，束流离子为40Ar+，缓冲气体为He气，模拟中的离子个数设为1 000，q=0.5，T=300 K，40Ar+离子在3°立体角中随机发射。RF四极电场频率分为250 kHz、500 kHz、1 MHz 3种。RFQ冷却聚束器中的缓冲气体气压远小于大气压。入射束流离子的动能和施加的缓冲气体气压能保证束流在RFQ1L缓冲气体中被完全冷却(1 keV，10 Pa；1 keV，5 Pa；1 keV，3 Pa；500 eV，3 Pa)，同时保证模拟过程中束流不能碰撞到电极。

模拟中，当束流完全冷却后，提取1 000个离子的信息，以离子的x(或y)方向的速度为纵坐标，离子在x(或y)轴的位置为横坐标作图，即束流冷却后的相图(图5～7)。

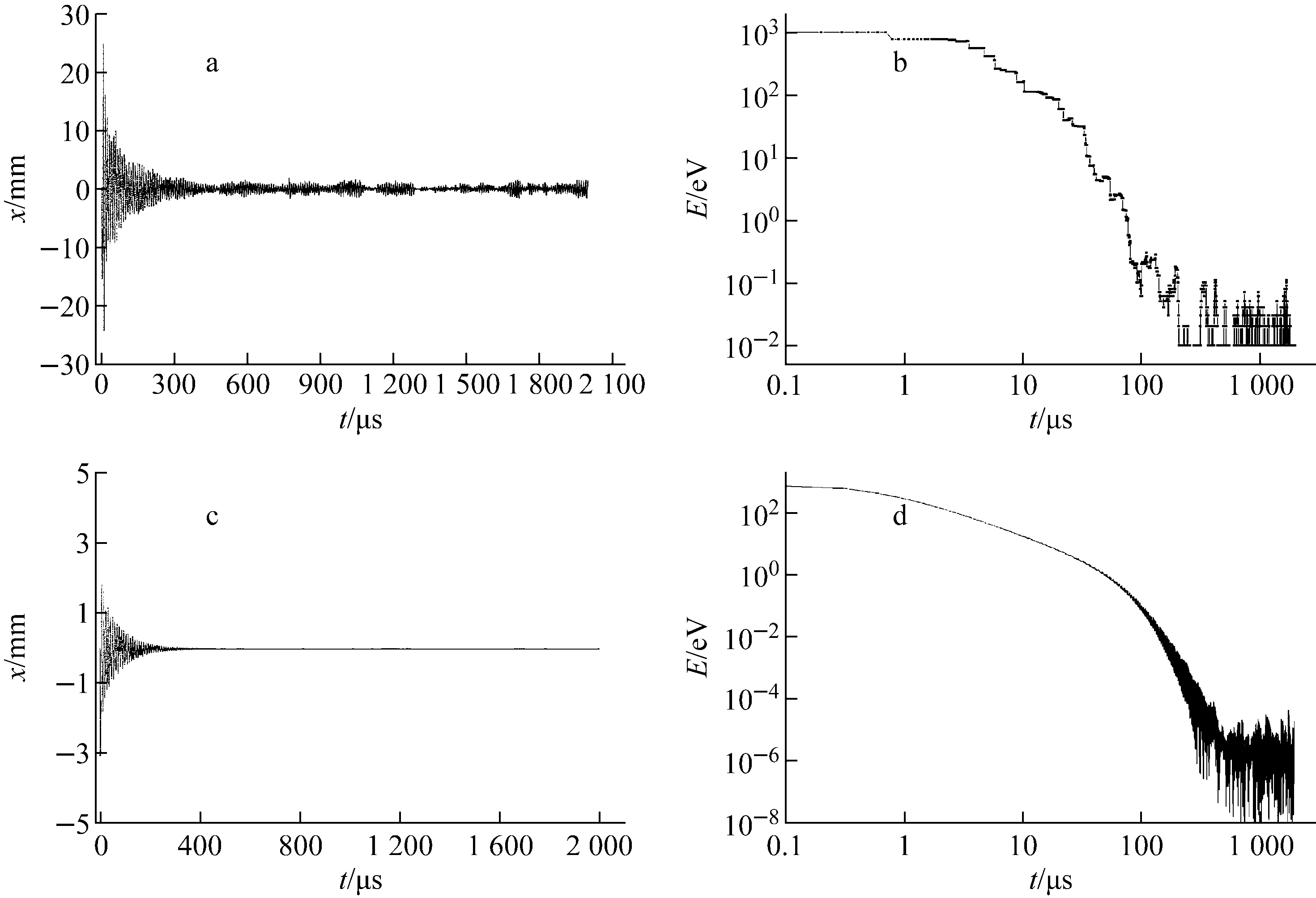
图4 RFQ冷却聚束器中40Ar+离子的运动幅度和能量随时间的变化

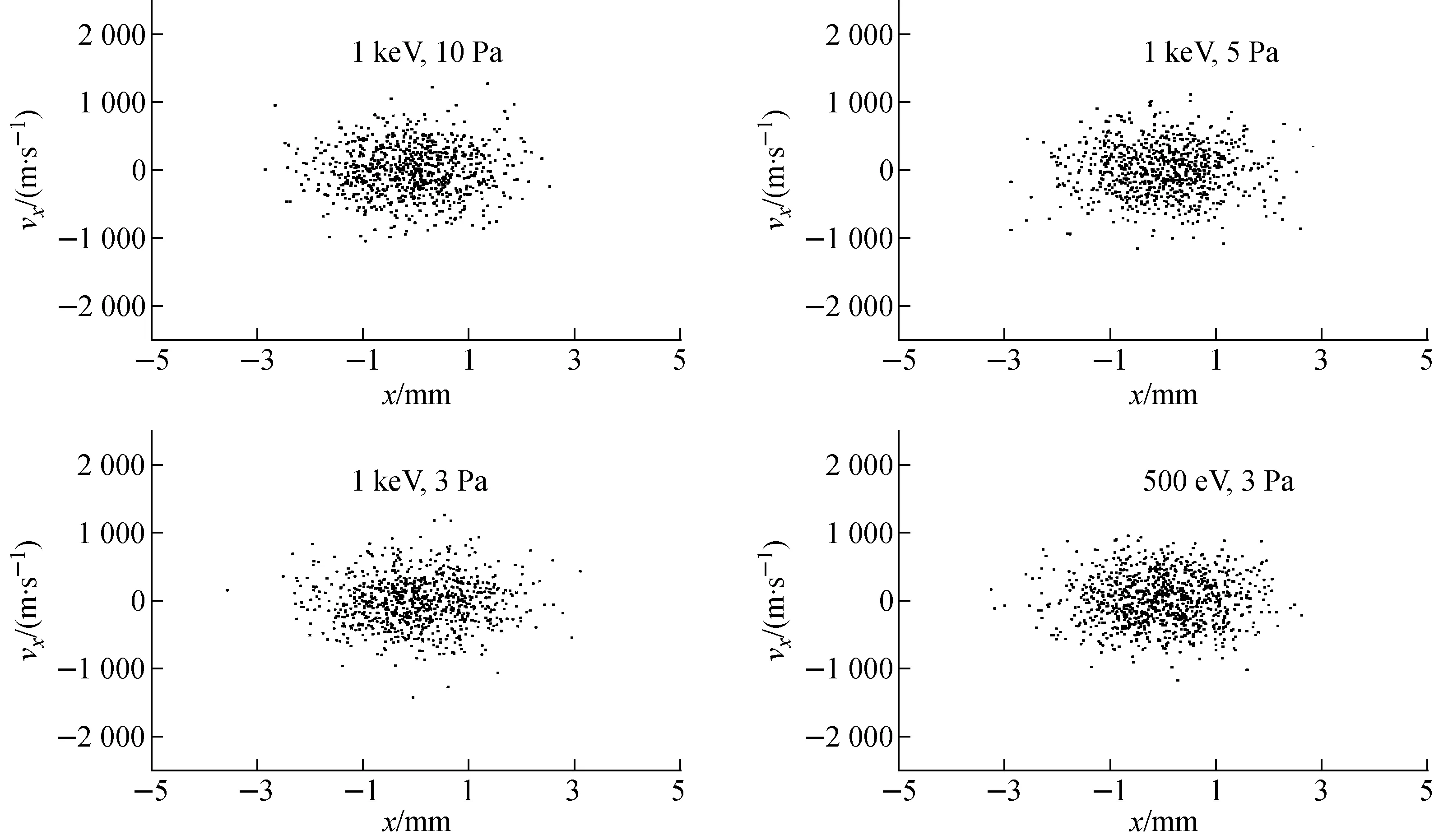
图5 f=250 kHz时不同能量和气压40Ar+束流完全冷却后的相图

从图5～7可看出，RF四极电场频率一定，不同能量的入射离子在不同缓冲气体气压下冷却，束流完全冷却后得到的束斑半径和能量分散相同。这说明，q、RF四极电场频率及T保持不变，即使入射束流能量、缓冲气体气压不同，束流在完全冷却后的能量分散和束斑半径却是相同的。

从图5～7还可看出，在250 kHz、500 kHz和1 MHz下，40Ar+离子束流在He气中冷却后的束斑半径分别约为3、1.5、0.75 mm。因此可得出，当q不变时，冷却后的束流束斑半径与RF四极电场频率呈反比。

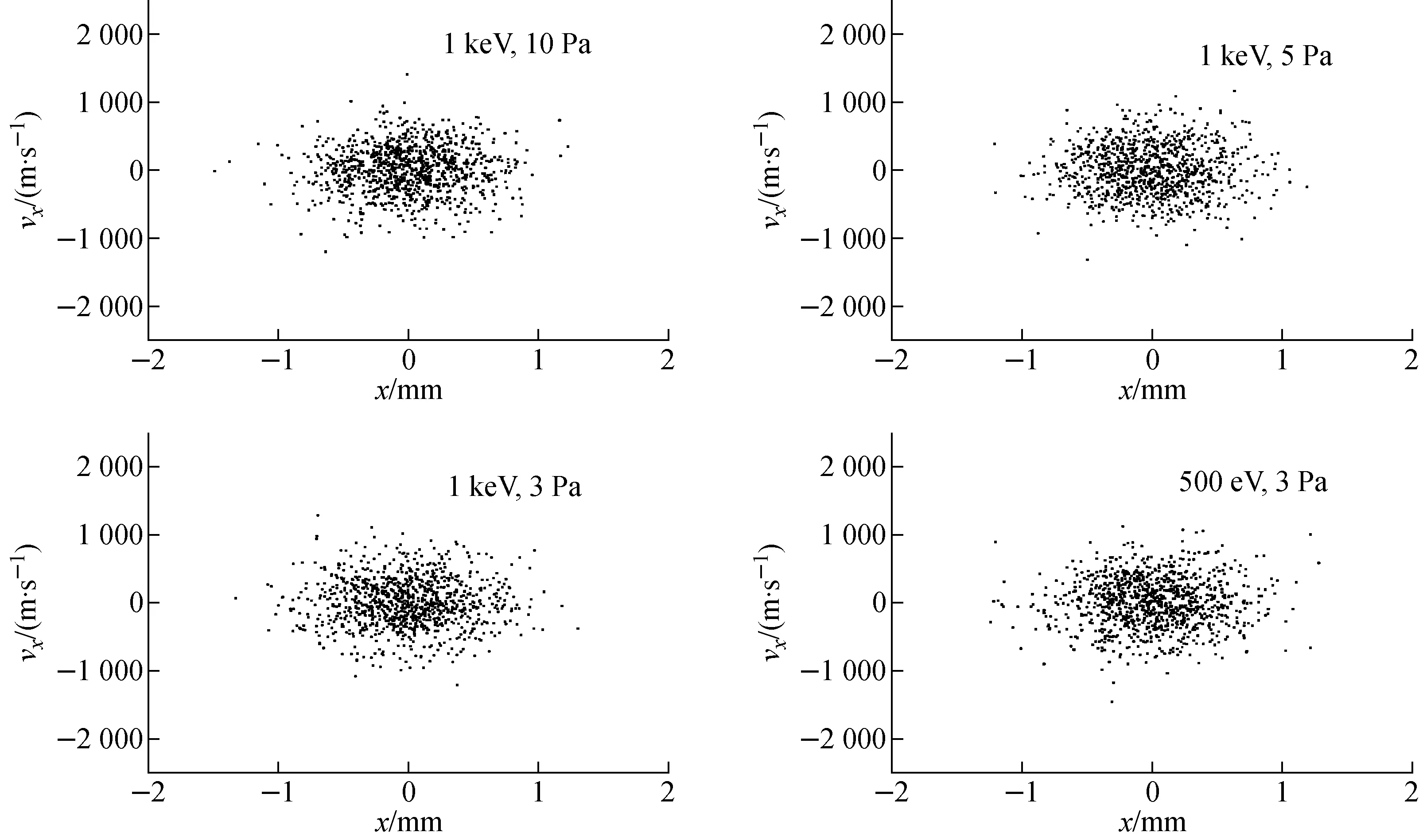
图6 f=500 kHz时不同能量和气压下40Ar+束流完全冷却后的相图

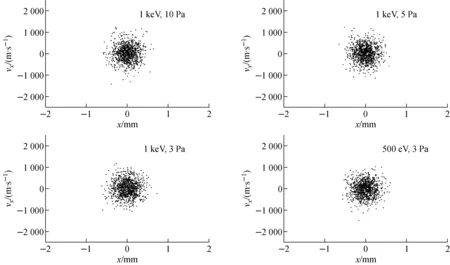
图7 f=1 MHz时不同能量和气压下40Ar+束流完全冷却后的相图

从图5～7还可看出，T=300 K保持不变，40Ar+束流在He气中被完全冷却后，束流的动能不随q、频率、电压、能量、气压的变化而变化。通过大量的模拟发现，当改变气体温度时能量分散会发生相应的变化。因此，完全冷却后的束流的能量分散仅与缓冲气体温度有关。

3.3 结果分析

1) 束流在完全冷却后，束斑保持一定，不随时间变化而变化；能量分散与缓冲气体保持热力学平衡，亦不随时间变化而变化。此结果与VDF模型[11,19]得到的结果不同，原因在于VDF模型过高地估计了离子冷却过程的有效性。在VDF模型下，只要冷却时间足够长，束斑可无限变小，且冷却后的束流能量可无限下降，直至10-12eV甚至更低。实际上，离子与缓冲气体最终会保持热力学平衡，离子只要还有一定动能，就会在RF四极电场的作用下振荡，具有一定运动幅度，且此运动幅度是与离子的热力学动能是相对应的，不随时间而减小。

2) 完全冷却后束流的能量分散和束斑半径与入射离子的能量及缓冲气体气压无关。无论束流的初始能量是多少，只要束流完全冷却，则冷却后束流的平均动能与缓冲气体的热力学平均动能相同，故冷却后束流的能量分散与束流的初始动能无关；而具有一定能量的离子，在RF四极电场中的运动幅度是一定的，故冷却后离子的束斑半径仅与缓冲气体的热力学平均动能和RF四极电场有关。缓冲气体气压的大小对束流传输有影响，但对冷却后束流的能量分散和束斑半径无影响。

3) 当q值不变时，冷却后的束流束斑半径与RF四极电场频率呈反比。冷却后的束流束斑半径与RF四极电场频率呈反比，此模拟结果与理论计算值相符合[20-21]，说明了RIP模型的准确性。高品质的束流要求能量分散小和束斑半径小，当束流完全冷却，其能量分散必然达到最小，此时束斑越小，束流品质越高。

4) 完全冷却后束流的能量分散仅与缓冲气体温度有关。缓冲气体的温度一定，Ar+离子与He气达到热力学平衡时，Ar+离子的平均动能即He气的热力学平均动能，所以完全冷却后束流的能量分散仅与缓冲气体的温度有关，不随其他条件改变而改变。

上述RIP模型得到的结果与理论计算值均相符，说明了RIP模型的准确性。上述模拟结果是40Ar+离子束流在He气中冷却得到的，当在模拟中不断改变离子的种类与缓冲气体的种类时，仍得到与上述一致的结论。

4 结论

本文采用国际上较先进的RIP模型进行蒙特卡罗模拟，得出束流在RFQ冷却聚束器中完全冷却后的性质。结果表明：束流在完全冷却后，束斑半径和能量分散保持一定，不随时间变化而变化；束流冷却后的能量分散和束斑半径不随缓冲气体气压、入射离子能量的变化而变化；冷却后束斑半径与RF四极电场频率呈反比；冷却后束流能量分散仅与温度有关。

参考文献：

[1] BOLLEN G, BECKER S, KLUGE H J, et al. ISOLTRAP: A tandem penning trap system for accurate on-line mass determination of short-lived isotopes[J]. Nucl Instrum Methods A, 1996, 368(3): 675-697.

[2] SIKLER G, ACKERMANN D, ATTALLAH F, et al. First on-line test of SHIPTRAP[J]. Nucl Instrum Methods B, 2003, 204(4): 482-486.

[3] KOLHINEN V S, ERONEN T, HAKALA J, et al. Penning trap for isobaric mass separation at IGISOL[J]. Nucl Instrum Methods B, 2003, 204(4): 502-506.

[4] SCHWARZ S, BOLLEN G, LAWTON D, et al. The low-energy-beam and ion-trap facility at NSCL/MSU[J]. Nucl Instrum Methods B, 2003, 204(4): 507-511.

[5] CLARK J, BARBER R C, BOUDREAU C, et al. Improvements in the injection system of the Canadian penning trap mass spectrometer[J]. Nucl Instrum Methods B, 2003, 204(4): 487-491.

[6] HUANG W X, ZHU Z C, TIAN Y L, et al. Progress on the RFQ1L and LPT[J]. Nuclear Physics Trends, 2010, 1235: 139-143.

[7] 黄文学，王玥，朱志超，等. 超重核研究谱仪的RFQ冷却聚束器RFQ1L[J]. 原子核物理评论，2006，23(4)：383-386.

HUANG Wenxue, WANG Yue, ZHU Zhichao, et al. RFQ cooler and buncher RFQ1L in super-heavy nuclide research spectrometer[J]. Nuclear Physics Review, 2006, 23(4): 383-386(in Chinese).

[8] 黄文学，王玥，徐瑚珊，等. RFQ冷却聚束器研究简介[J]. 原子核物理评论，2005，22(3)：254-260.

HUANG Wenxue, WANG Yue, XU Hushan, et al. Brief introduction of RFQ cooler and buncher[J]. Nuclear Physics Review, 2005, 22(3): 254-260(in Chinese).

[9] DAWSON P H. Quadrupole mass spectrometry and its applications[M]. Amsterdam: Elsevier Scientific Publish Company, 1976.

[10] LUNNEY M D, MOORE R B. Cooling of mass-separated beams using a radiofrequency quadrupole ion guide[J]. International Journal of Mass Spectrometry, 1999, 190(8): 153-160.

[11] KIM T. Buffer gas cooling of ions in a radio frequency quadrupole ion guide[D]. Montreal: McGill University, 1997.

[12] BUI H A, COOKS R G. Windows version of the ion trap simulation program ITSIM: A powerful heuristic and predictive tool in ion trap mass spectrometry[J]. Journal of Mass Spectrometry, 1998, 33(4): 297-304.

[13] SCHWARZ S. IonCool: A versatile code to characterize gas-filled ion bunchers and coolers (not only) for nuclear physics applications[J]. Nucl Instrum Methods A, 2006, 566(2): 233-243.

[14] SCHWARZ S. Simulations for ion traps: Buffer gas cooling, Vol 749[M]. Berlin Heidelberg: Springer-Verlag, 2008: 1-21.

[15] MASON E A, McDANIEL E W. Transport properties of ions in gases[M]. New York: Wiley, 1988.

[16] ELLIS H W, McDANIEL E W, ALBRITTON D L, et al. Transport properties of gaseous ions over a wide energy range, Part Ⅱ[J]. Atomic Data and Nuclear Data Tables, 1978, 22(3): 179-217.

[17] ELLIS H W, THACKSTON M G, McDANIEL E W, et al. Transport properties of gaseous ions over a wide energy range, Part Ⅲ[J]. Atomic Data and Nuclear Data Tables, 1984, 31(1): 113-153.

[18] ZHU Z C, HUANG W X, SUN Y L, et al. Energy limitation for models to simulate the buffer gas cooling[J]. International Journal of Mass Spectrometry, 2012, 309(1): 44-48.

[19] VIEHLAND L A, MASON E A. Transport properties of gaseous ions over a wide energy range, Part Ⅳ[J]. Atomic Data and Nuclear Data Tables, 1995, 60(1): 37-95.

[20] 朱志超. RFQ冷却聚束器RFQ1L的缓冲气体冷却和束流传输[D]. 北京：中国科学院研究生院,2011.

[21] SCHMIDT S. REXTRAP: Ion accumulation, cooling and bunching for REX-ISOLDE[D]. Mainz: Johannes Gutenberg-Universität in Mainz, 2001.