转子/定子碰摩系统的非线性模态及其在干摩擦反向涡动响应预测中的应用

陈艳华,江俊

(西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安)

转子/定子碰摩系统的非线性模态及其在干摩擦反向涡动响应预测中的应用

陈艳华,江俊

(西安交通大学机械结构强度与振动国家重点实验室, 710049, 西安)

为了分析转子/定子碰摩系统中的非线性模态,确定交叉耦合效应对非线性模态的影响以及非线性模态在预测系统干摩擦反向涡动响应中的作用,针对一个考虑了定子运动学特性以及转子和定子间交叉耦合效应的四自由度转子/定子碰摩系统,用解析方法求解了其线性和非线性模态,分析了系统干摩擦反向涡动响应的涡动频率,确定了激发干摩擦反向涡动的临界速度与系统模态之间的关系。分析结果表明:系统存在2个负的线性模态频率;随着碰摩面摩擦系数的增大,其负的非线性模态频率由1个增加到3个;系统的2个负线性模态频率不但是相应非线性模态的边界,也是干摩擦反向涡动频率的上边界;非线性模态存在的最小摩擦系数就是发生干摩擦反向涡动失稳的最小摩擦系数。此项研究可为转子/定子碰摩系统的响应预测提供新的思路。

非线性模态;干摩擦反向涡动响应;临界速度;涡动频率

旋转机械中的碰摩故障是指运行中的转子与定子发生碰撞摩擦,这种故障可以发生在转子的某一处(单点碰摩)或多处(多点碰摩)。碰摩通常是由于机械系统的其他故障引起的,例如转子系统装配误差、定子的变形或运动、转轴的局部弯曲、转子质量不平衡激励等。碰摩故障轻则引起设备的异常振动、磨损,重则造成整个机器破坏甚至灾难性的事故。在现代新型旋转机械中,由于转子/定子间隙的减小、更加柔性的转子结构以及高负荷的工作环境,也使得旋转机械中的碰摩风险大大增加[1]。

鉴于旋转机械中碰摩风险的增大,以及碰摩动力学问题的复杂性和响应行为的丰富性,关于转子与定子碰摩的研究受到了人们的高度重视。文献[2]系统回顾了20世纪90年代之前关于转子/定子碰摩的研究成果,并对转子/定子碰摩过程的建模和碰摩动力学响应行为进行了归类。文献[3]对转子/定子碰摩研究中有关特定系统参数对碰摩响应的影响、碰摩效应(碰摩对系统性质的影响)和典型响应行为进行了粗略的归纳。文献[4]从转子/定子碰摩响应的典型非线性动力学响应特征出发,对相关的转子与定子碰摩的研究成果进行了综述。

在转子/定子系统中,当激励力的方向与转子涡动速度切向相同时,就可能引起转子失稳。若这类切向力的大小与转子的径向位移成比例,就称为交叉耦合刚度力。透平机中的气尖力或轴承油膜力都可以带来交叉耦合效应[5-6]。Day在研究了含轴承间隙和交叉耦合刚度系数的Jeffcott转子系统后指出:由于交叉耦合刚度系数的存在,系统存在非线性固有频率[7]。

在针对碰摩反向涡动响应的研究中,假设自激响应的解为待求频率的谐波解的形式,并去掉方程的激励项,则以自由振动的方式可以求解转子/密封件耦合系统的固有频率[8]。江俊在文献[9]中给出了一类转子与定子耦合系统的非线性固有频率,揭示了系统准周期碰摩响应演变为干摩擦反向涡动响应的物理机制——转子系统在负的非线性固有频率处发生了共振,并且发现,转子与定子耦合系统的非线性固有频率正是反向全周涡动响应在临界激励转速下的涡动频率。他还研究了转子/定子耦合系统的线性和非线性模态的相互作用机制,发现非线性模态频率与线性模态频率在转速-摩擦系数参数平面内存在交点,该交点对应的摩擦系数值是发生干摩擦反向全周涡动响应的最小值[10]。针对含交叉耦合效应的四自由度转子/定子碰摩系统,Shang等分析了其同频全周碰摩解的稳定性,得出了交叉耦合效应对全周碰摩响应的影响规律[11]。

对转子/定子碰摩系统的非线性模态进行分析,目的之一是使其发挥类似于线性模态的作用,用于了解系统的激励与响应的关系,防止碰摩失稳的发生。Childs等将Black反向涡动模型[12]推广到多模态的转子/定子模型,并对Bartha的实验模型[1]进行了预测,预测所得系统的涡动频率与实验结果非常接近[13]。江俊等在研究转子/定子碰摩时,在含有阻尼项的非线性自由振动方程中,得到了非同步通过平衡位置和最大位置的非线性模态[14]。陈艳华等解析求解了二自由度转子/定子碰摩系统的非线性模态,并用数值模拟进行了验证[15]。上述研究成果为进一步探索用非线性模态预测碰摩响应提供了基础。

本文针对考虑了定子运动学特性及交叉耦合效应的转子/定子系统,分析其非线性模态,着重研究交叉耦合刚度对系统非线性模态的影响,并使用非线性模态来预测系统干摩擦反向涡动响应的特性。

1 系统模型与运动方程

本文研究的转子/定子碰摩系统考虑了定子的运动学特性,如图1所示。系统转轴的刚度为kr,由轴承支撑,不考虑转轴的质量;质量为mr的刚性转子放置在轴承跨距中间,转子质心对其几何中心的偏心距为e;定子的径向刚度为ks,质量为ms,定子内环面的接触刚度为kc,表面的摩擦系数为μ;转子和定子之间的间隙为δ。

考虑定子运动学特性的转子/定子系统意味着定子的支撑是弹性的,并且要考虑定子的质量。在实际情况下,定子的转动惯性非常微小,可以忽略不计。在计及交叉耦合效应时,系统的运动方程可以表示如下

(1)

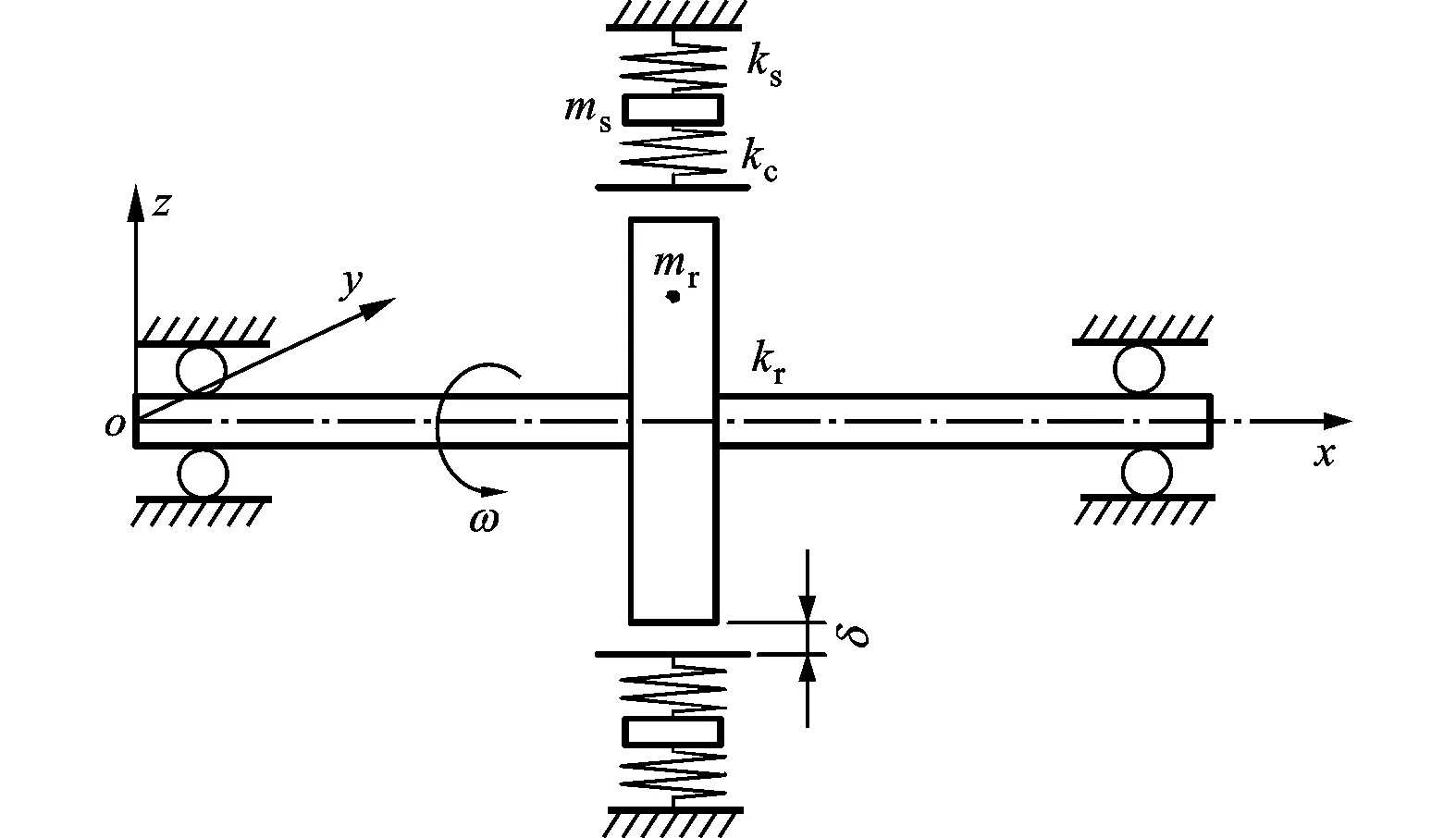
(a)转子/定子系统的主要参数

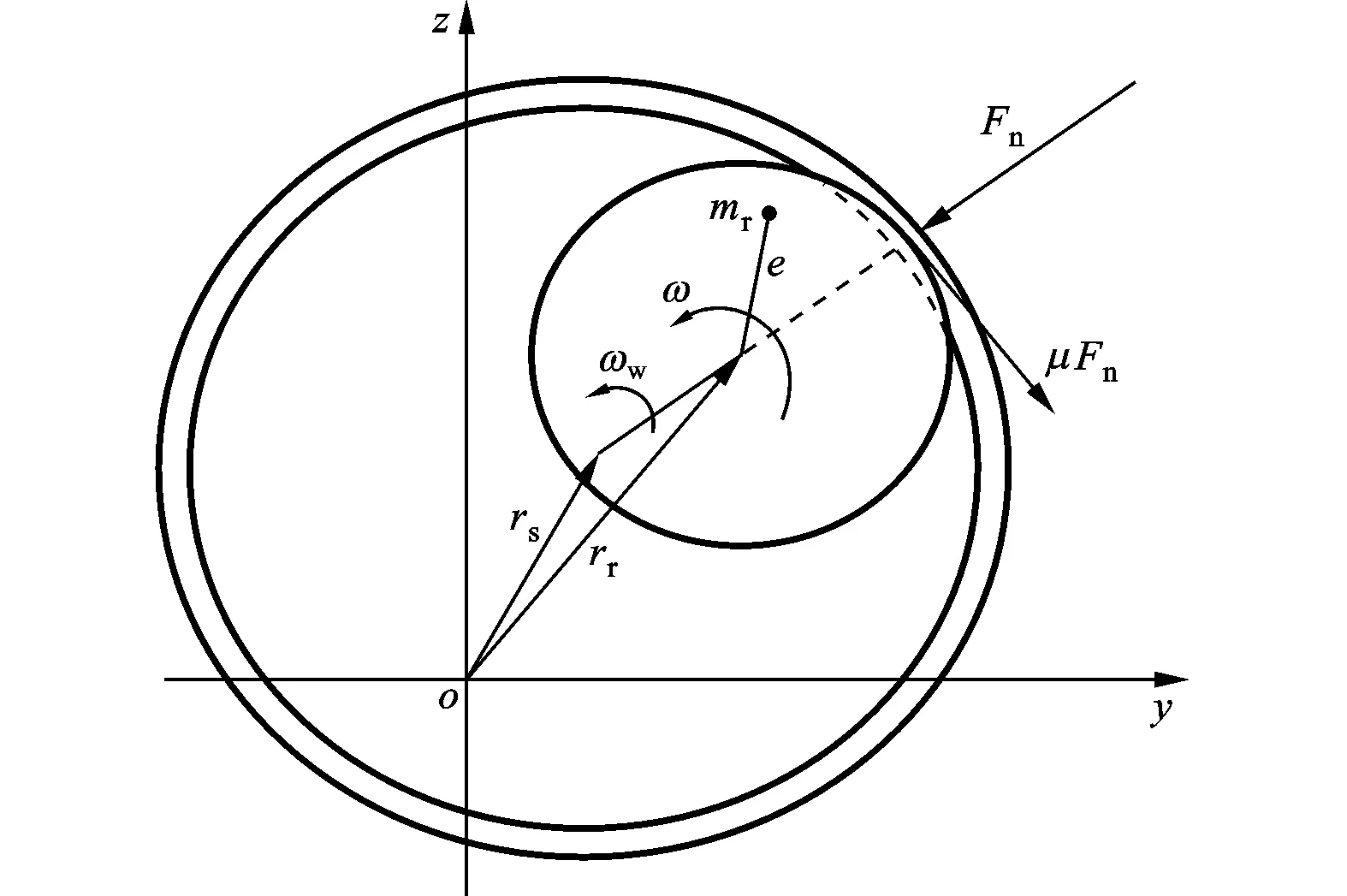
(b)碰摩转子系统的受力情况

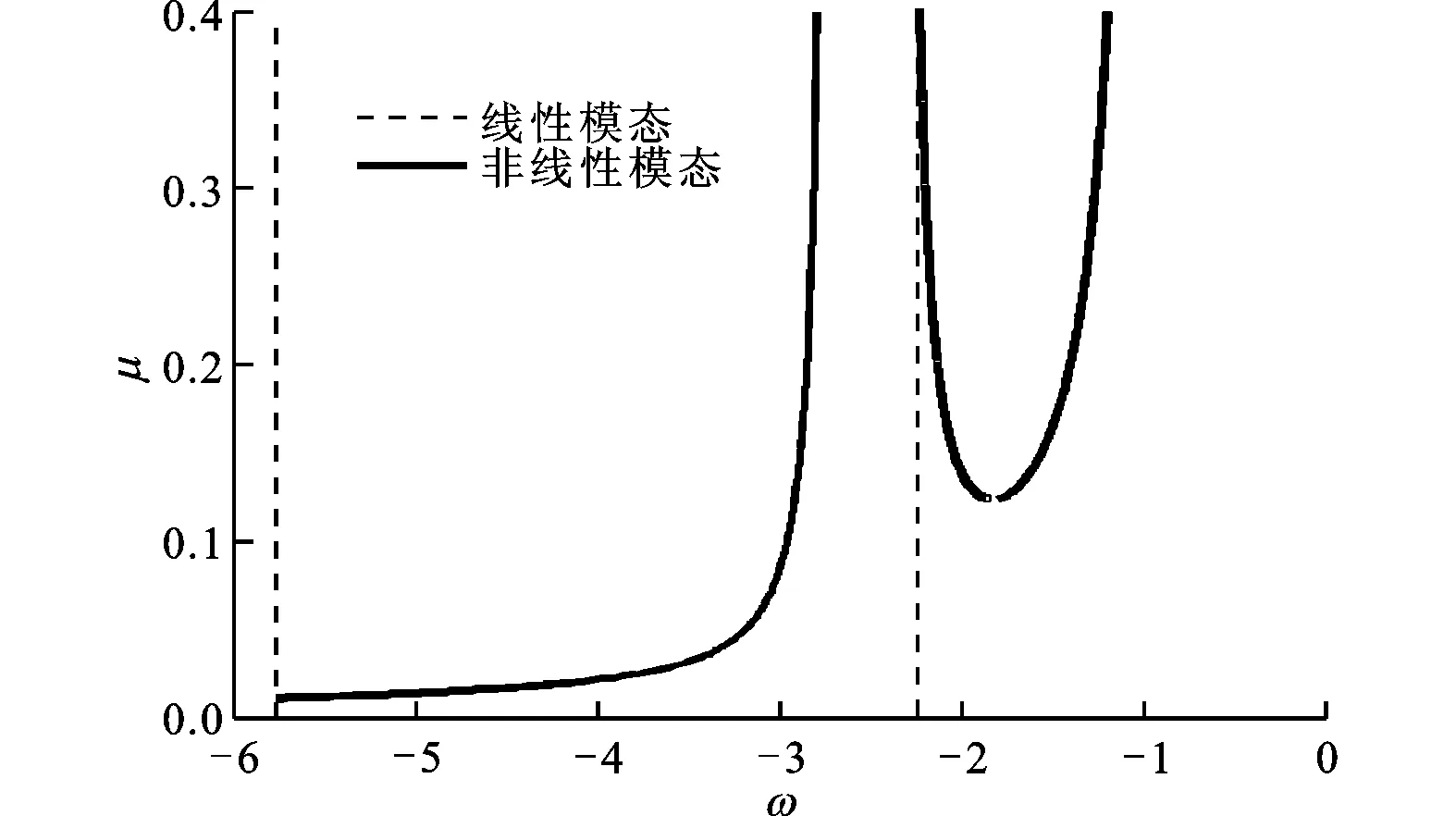
式中:转子与定子碰摩力的合力

vrel=rdiskω+|rr-rs|ωw

rr=yr+jzr和rs=ys+jzs分别表示转子、定子的总变形;νr和νs分别表示转子、定子的交叉耦合阻尼项,Qr和Qs分别表示转子、定子的交叉耦合刚度项,这4个参数组合起来表达交叉耦合效应;Θ为Heaveside函数

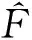
(2)

式中各归一化变量定义如下

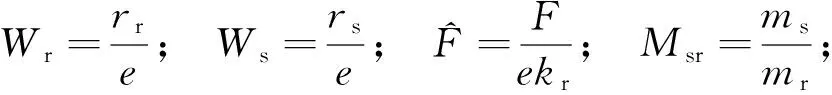
2 耦合系统的模态频率

2.1 线性耦合系统的模态频率

将方程中的交叉耦合效应略去,并设转子/定子间的间隙为0,使转子与定子能耦合到一起。为了将方程简化为线性碰撞系统,略去干摩擦效应,并将碰摩力简化为简单的线性形式,同时略去激励项,可以得到转子/定子线性耦合时的模态方程

(3)

方程(3)的解可以假设为如下形式

Wr=Arejωlτ;Ws=Asejωlτ

式中:ωl为线性模态频率。将解代入方程(3),可以得到关于模态频率的特征方程

βsrβcr+βsr+βcr=0

(4)

求解方程(4),可以得到转子/定子耦合系统的线性模态频率

式中

S1=Msr(1+βcr)+(βsr+βcr)

S2=4Msr[βsrβcr+(βsr+βcr)]

求得的模态频率成对出现,符号相反。在转子/定子碰摩系统中,模态频率为正意味着转子的振动或涡动方向与其自转的方向一致,模态频率为负则表示转子的振动或涡动方向与其自转方向相反。

2.2 非线性耦合系统的模态频率

从方程(2)出发来分析系统的非线性模态。首先省略激励项,并假设转子/定子的非线性模态频率及振幅分别为ωn、Hr和Hs,因此方程的模态解可以写为

Wr=Hrejωnτ;Ws=Hsej(ωnτ+φ)

式中:φ为转子/定子振动的相位差。将解代入方程(2)并合并同类项,可得

(5)

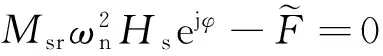
(6)

将式(5)与式(6)相加,可求得Hr与Hs的关系

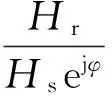
(7)

式中

将式(7)代入式(6)并化简可得

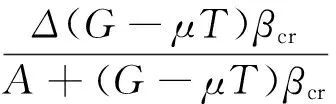
(8)

式中

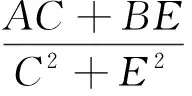
联立式(6)、式(7)和式(8),可求得非线性模态频率的特征方程(9)。当此方程的实数根满足碰摩条件(即|Wr-Ws|>δ)时,它就是有意义的非线性模态频率。因此,只要给定系统参数,就可以求解其非线性模态频率。

(9)

式中

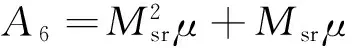
根据方程(4)和(9)的解可以绘制系统的线性模态与非线性模态。图2展示了系统线性模态与非线性模态之间的关系，鉴于本文的研究内容，此处只绘制了负的非线性模态频率。

从图2中可以看出,系统存在2个负的耦合线性模态频率,而系统耦合的非线性模态频率数量随着摩擦系数的增大而增多。当摩擦系数在[0.01,0.12]的范围内时,系统只存在1个非线性模态频率;当摩擦系数大于0.12时,系统有3个负的非线性模态频率共存。另一方面,线性模态频率可以作为对应非线性模态频率的下边界。

ζr=0.02; ζs=0.01; Msr=2.052 6; βsr=15.319;Rdisk/Δ=2.66; βcr=20; κr=0.12; κs=γr=γs=0

3 干摩擦反向涡动响应特性

3.1 反向涡动频率

在转子/定子系统中,干摩擦反向涡动是一种自激振动响应形式,此时转轴的涡动方向与转速方向相反。由于存在质量偏心,系统响应中仍然包含正向涡动频率成分,但是与反向涡动相比较而言,正向涡动响应的幅值很小,几乎可以忽略。

设Wb、Wf分别表示自激反向涡动响应与受迫正向涡动响应,则系统总的响应可以写成

Wi=Wbi+Wfi,i=r,s

(10)

式中:Wbi=Hie(α+jωb)τ+jφi;Wfi=GiejΩτ;ωb为反向涡动频率;r和s分别表示转子和定子;Hieατ是随时间变化的幅值成分,当α大于0时,系统处于干摩擦的反向涡动状态。在转子/定子碰摩系统中,定子与转子之间的相位差对了解系统状态很有价值,不失一般性,设φr=0,φs=φ。另一方面,由于本文主要研究干摩擦反向涡动响应的特性,因而忽略由于不平衡质量引起的同向涡动频率成分,所以系统的响应可以简化成如下形式

Wbr=Hre(α+jωb)τ;Wbs=Hse(α+jωb)τ+jφ

(11)

此外,当系统出现干摩擦反向涡动响应时,可以近似认为转子与定子之间保持纯滚动,即满足

|Wr-Ws|=|(Wbr+Wfr)-(Wbs+Wfs)|=

(12)

将式(11)、式(12)代入方程(2)并省略不平衡质量的激励项,就可以得到转子/定子系统干摩擦反向涡动响应的控制方程

(α+jωb)2Hr+(1-jκr)Hr+

(2ζr-jγr)(α+jωb)Hr+

βcr(1+jμ)(1+EΔ)(Hr-Hsejφ)=0

(13)

Msr(α+jωb)2Hsejφ+(βsr-jκs)Hsejφ+

(2ηs-jγs)(α+jωb)Hsejφ-

βcr(1+jμ)(1+EΔ)(Hr-Hsejφ)=0

(14)

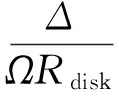
将方程(13)、(14)相加,可以得到转子与定子涡动响应下的幅值关系

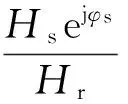
(15)

式中:P、Q、M、N都是与系统干摩擦反向涡动频率相关的参数。

Q=2αωb+2ζrωb-γrα-κr

N=2αωbMsr+2ωbηs-αγs-κs

将方程(15)代入方程(13),可得

(16)

分离方程(16)的虚部、实部可得

(17)

将P、Q、M、N的表达式代入方程(17),可以得到包含ωb与α的方程组,在给定激励频率Ω的情况下,求解此方程组就可以求得ωb与α。当α>0时,所对应的ωb即为系统在此激励下的反向涡动频率。在转子/定子碰摩系统中,碰摩面间的摩擦系数是影响反向涡动响应特性的重要参数。当不考虑转子/定子之间的交叉耦合效应时,在较大的摩擦系数下,对应同一个激励转速,系统会存在2个反向涡动响应状态,且2个状态之间会发生跳跃[16]。针对不考虑定子动力学特性的二自由度转子/定子系统的研究发现,如果转子/定子间存在交叉耦合刚度效应,则系统在较大的摩擦系数下才会出现干摩擦反向涡动失稳[15]。

图3给出了不同激励转速下系统的干摩擦反向涡动频率。图3b中虚线所对应的正是耦合系统的线性模态频率,可以作为系统的反向涡动频率的上界。从图3a、3b的对比中可以看出,当转子上存在交叉耦合刚度效应时,系统的低阶反向涡动只是在Ω<2.5的转速范围内存在,而当系统中不存在交叉耦合刚度时,这一反向涡动频率能在很大的转速范围内存在。这说明,转子上的交叉耦合刚度系数可以有效抑制低阶反向涡动响应的范围。

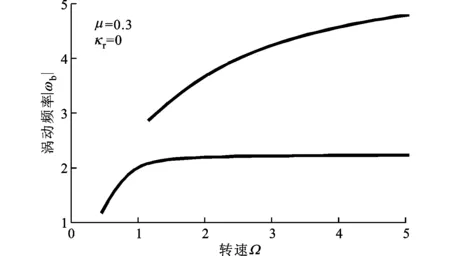
(a)不考虑交叉耦合效应[16]

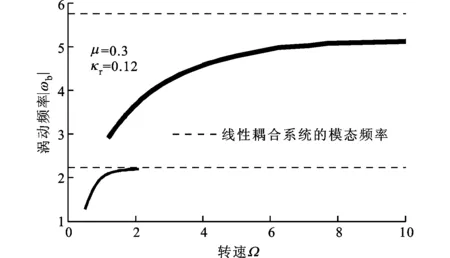
(b)考虑转子上的交叉耦合刚度μ=0.3; ζr=0.02; ζs=0.01; Msr=2.052 6; βsr=15.319;Rdisk/Δ=2.66; βcr=20; κr=0.12; κs=γr=γs=0

3.2 反向涡动响应的激励转速边界

从前面的分析可以看出,当α>0时系统出现干摩擦反向涡动,则α=0所对应的转速即为干摩擦反向涡动响应出现的临界转速。本文在推导方程(17)时,将受迫激励引起的正向涡动幅值Wfr和Wfs略去,主要是考虑在干摩擦反向涡动这种自激响应状态下,受迫激励的幅值相对很小,即使是在转速较高的情况下亦很小。因此,将α=0代入方程(17),消去C后可以得到α=0条件下的频率ωb方程(18),求得ωb之后将其回代入方程(17)中的任意一式可以求得C,再根据C即可求解出临界转速Ω的值。

(18)

式中

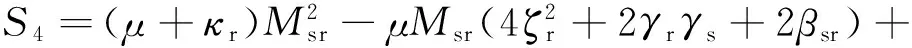
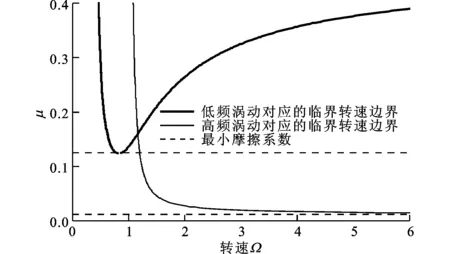
κr=0.12; ζr=0.02; ζs=0.01; Msr=2.052 6; βsr=15.319;Rdisk/Δ=2.66; βcr=20; κr=0.12; κs=γr=γs=0

图4给出了摩擦系数对临界转速边界的影响。从图中可以看出,系统有2个干摩擦反向涡动状态,其临界转速边界分别由粗实线和细实线表示。通过数值模拟发现,即使在较高的转速下,本文方法预测的临界转速边界的精度依然很高。图中粗实线对应的临界转速边界表明,当系统的摩擦系数大于0.125时,低涡动频率的反向涡动响应只在一个“U”形的转速范围存在。图中细实线对应的临界转速边界是一个“L”形的区间,当摩擦系数大于0.01时,在L形曲线内的区域存在着高涡动频率的反向涡动响应。对应2种干摩擦反向涡动响应出现的2个最低的摩擦系数值,正是系统出现非线性耦合模态频率所需的最小摩擦系数值,也是线性模态频率曲线与非线性模态频率曲线交点处的摩擦系数值。

4 结 论

本文建立了考虑定子的运动特性以及转子与定子之间的交叉耦合效应的转子/定子碰摩模型,求得了系统线性、非线性模态频率的解析解。通过分析发现,此系统存在2个负的线性模态频率,而非线性模态频率的数量与摩擦系数的大小有关:当摩擦系数较小时,只存在1个负的非线性模态频率;当摩擦系数大于0.12之后,系统存在3个负的非线性模态频率。系统的2个线性模态频率都可以作为对应非线性模态频率存在的约束边界。

本文求得了转子上存在交叉耦合刚度效应时系统的干摩擦反向涡动频率。在选定的系统参数下,系统存在2个干摩擦反向涡动频率,而系统的线性模态频率就是干摩擦反向涡动频率的上限值,这为干摩擦反向涡动频率的初步估计提供了依据。与不考虑交叉耦合刚度效应的情况相比,交叉耦合刚度可以明显抑制低频的干摩擦反向涡动响应范围。

本文还确定了干摩擦反向涡动响应的激励速度边界。此速度边界对应的最小摩擦系数正是系统出现非线性模态频率的摩擦系数,也是非线性模态与线性模态频率交点处的摩擦系数。

[1] BARTHA A R. Dry friction backward whirl of rotors [D]. Zurich, Switzerland: Swiss Federal Institute of Technology Zurich, 2000.

[2] MUSZYNSKA A. Rotor-to-stationary element rub- related vibration phenomena in rotating machinery: literature survey [J]. Sound and Vibration Digest, 1989, 21(3): 3-11.

[3] SAGHEER A. Literature survey: rotor casing contact phenomenon in rotor dynamics [J]. Journal of Vibration and Control, 2010, 16(9): 1369-1377.

[4] 江俊, 陈艳华. 转子与定子碰摩的非线性动力学研究 [J]. 力学进展, 2013, 43(1): 132-148. JIANG Jun, CHEN Yanhua. Advances in the research on nonlinear phenomena in rotor/stator rubbing systems [J]. Advances in Mechanics, 2013, 43(1): 132-148.

[5] JIANG J, ULBRICH H. Stability analysis of sliding whirl in a nonlinear Jeffcott rotor with cross-coupling stiffness coefficient [J]. Nonlinear Dynamics, 2001, 24(3): 269-283.

[6] CHU Fulei, ZHANG Zhengsong. Periodic, quasi-periodic and chaotic vibrations of a rub-impact rotor system supported on oil film bearings [J]. International Journal of Engineering Science, 1997, 35(10/11): 963-973.

[7] DAY W B. Asymptotic expansions in nonlinear rotordynamics [J]. Quarterly of Applied Mathematics, 1987, 44(4): 779-792.

[8] MUSZYNSKA A. Whirl and whip-rotor/bearing stability problems [J]. Journal of Sound and Vibration, 1986, 110(3): 443-462.

[9] JIANG Jun. The physical reason and the analytical condition for the onset of dry whip in rotor-to-stator contact systems [J]. ASME Journal of Vibration and Acoustics, 2005, 127(6): 594-603.

[10]JIANG Jun. The interplay of linear and nonlinear modes on the dynamics of a rotor/stator contact system [C]∥Proceedings of the 8th IFToMM International Conference on Rotordynamics. Seoul, Korea: KIST, 2010: 12-15.

[11]SHANG Zhiyong, JIANG Jun, HONG Ling. The influence of the cross-coupling effects on the dynamics of rotor/stator rubbing [M]∥Dynamical Systems, Discontinuity, Stochasticity and Time-Delay. Berlin, Germany: Springer, 2010: 121-132.

[12]BLACK H. Interaction of a whirling rotor with a vibrating stator across a clearance annulus [J]. Journal of Mechanical Engineering Science, 1968, 10(1): 1-12.

[13]WILKES J C, DYCK B J, CHILDS D W, et al. The numerical and experimental characteristics of multi-mode dry-friction whip and whirl [C]∥Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea and Air GT2009. Orlando, Florida, USA: ASME, 2009: 8-12.

[14]JIANG Jun, WU Zhiqiang. Determine the characteristics of a self-excited oscillation in rotor/stator systems from the interaction of linear and nonlinear normal modes [J]. International Journal of Bifurcation and Chaos, 2010, 20(12): 4137-4150.

[15]CHEN Yanhua, JIANG Jun. Determination of nonlinear normal modes of a planar nonlinear system with a constraint condition [J]. Journal of Sound and Vibration, 2013, 332: 5151-5161.

[16]JIANG Jun, SHANG Zhiyong, HONG Ling. Characteristics of dry fiction backward whirl: a self-excited oscillation in rotor-to-stator contact systems [J]. Science China: Technological Science, 2010, 53(3): 674-683.

(编辑 葛赵青)

DeterminationofNonlinearNormalModeswithApplicationstoPredictionofDryFrictionBackwardWhirlMotionofaRotor/StatorRubbingSystem

CHEN Yanhua,JIANG Jun

(State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

To determine the nonlinear normal modes(NNMs) and investigate the influence of cross-coupling effect on the NNMs as well as the function of NNMs in predicting dry friction backward whirl response in rotor/stator rubbing systems, a four-degree freedom rotor/stator rubbing system with the consideration of dynamics of the stator and the cross-coupling effects is investigated. Linear and nonlinear normal modes of the system are derived analytically, and the relationship between the whirl frequency and the critical rotating speed of the dry-friction backward whirl is exploited. It is found that the system possesses two linear normal modes and its negative NNMs vary from one to three with the increasing friction coefficient on the contact surface; the linear modal frequencies work not only as the existence boundaries of NNMs, but also as the upper limits of the whirl frequencies of the dry-friction backward whirl motion. Moreover, the minimal friction coefficient for the existence of the nonlinear normal modes is just the minimal friction coefficients for occurrence of the dry friction backward whirl motion. The results may facilitate providing a new prospective method for response prediction in rotor/stator rubbing systems.

nonlinear normal mode; dry friction backward whirl motion; critical rotating speed; whirl frequency

10.7652/xjtuxb201405015

2013-09-21。 作者简介: 陈艳华(1985—),男,博士生;江俊(通信作者),男,教授,博士生导师。 基金项目: 国家自然科学基金资助项目(11172223)。

时间: 2014-03-05 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140305.1118.005.html

TM301.4;O327

:A

:0253-987X(2014)05-0082-07