三参数边界强度过程模型及其在数控机床可靠性评估中的应用
任丽娜,芮执元,李建华,李海燕
(1.兰州理工大学机电工程学院, 730050, 兰州; 2.电子科技大学机械电子工程学院, 611731, 成都)
三参数边界强度过程模型及其在数控机床可靠性评估中的应用
任丽娜1,2,芮执元1,李建华1,李海燕1
(1.兰州理工大学机电工程学院, 730050, 兰州; 2.电子科技大学机械电子工程学院, 611731, 成都)
为提高数控机床可靠性评估的准确性,基于边界强度过程理论,提出一种初始时刻故障强度不为零的三参数边界强度过程模型。通过对故障强度函数进行求导运算,证实了模型的特性,并推导了三参数边界强度过程和齐次泊松过程之间的关系。利用极大似然估计法和优化方法,给出了模型参数及可靠性指标的计算公式。分别以单台数控机床故障截尾数据和多台数控机床时间截尾数据为例对模型进行验证,对数似然函数及拟合优度计算结果均表明:三参数边界强度过程模型优于边界强度过程模型,而且更符合工程实际,可为制定合理的维修策略提供一定的理论依据。
三参数边界强度过程;极大似然估计;数控机床;可靠性评估
数控机床是由众多零部件组成的复杂机电系统,是典型的可修复系统。对于可修复系统,维修行为贯穿于其使用的全过程,且不同的维修行为对系统的可靠性有不同程度的影响。通常情况下,系统维修活动仅涉及其中部分零部件,从而使系统修复后处在与故障前近似相同的状态[1],在这种最小维修情况下,通常采用幂律过程[2-4]和对数线性过程[5]等非齐次泊松过程(non-homogenous Poisson process,NHPP)来描述可修系统的故障过程,但这两种过程模型的共性问题是随着工作时间的增加,故障强度均无限增大。实际上,当可修复系统进入耗损期后,随着可靠性的下降,维修频次也相应地增加,由于频繁地对系统故障零部件进行最小维修,使得系统的故障强度有时为有界增函数,而非无限增大[6]。针对这种维修频繁的可靠性恶化系统,Pulcini提出了一种边界强度过程(BIP)模型[7],该模型是二参数非齐次泊松过程模型的一种,其故障强度随系统运行时间的增加渐近于某一常数,适用于评估处于耗损期可修复系统的可靠性。文献[8]通过实例验证了BIP模型适用于描述处于耗损期的数控机床故障过程。但是,该模型在零时刻时故障强度为零,这与工程实际不符,因为开始对现场故障数据进行采集时,机床已经或即将进入耗损期,由于磨损、疲劳及老化等的存在,数据采集初始时刻故障强度一般不为零,即此时的机床一般不是“完美无缺”的。因此,若按该模型建模,可能会导致评估结果准确度低、易造成制定不合理的维修策略等问题。
为提高数控机床可靠性评估的准确性,本文根据数控机床故障机理,在边界强度过程模型的基础上,引入位置参数,建立三参数边界强度过程模型,实现了最小维修假设下数控机床可靠性的有效评估。
1 三参数边界强度过程模型
1.1 模型建立
边界强度过程模型是数控机床可靠性分析的备选模型之一,其强度函数λ(t)定义为
λ(t)=α(1-exp(-t/β)),α,β>0,t≥0
(1)
λ(t)为一有界增函数,表示系统在单位时间内发生故障的次数。当t=0时,λ0=0,表示系统在该时刻是“完美”的,当t→∞时,λ(t)|t→∞=α,α即为系统最大故障强度。
考虑到浴盆曲线的损耗阶段之前是偶然故障阶段,故障强度不为零,为更好地解决工程实际问题,本文在BIP模型的基础上,通过引入位置参数,提出三参数边界强度过程模型,其故障强度函数λ(t)定义为
(2)
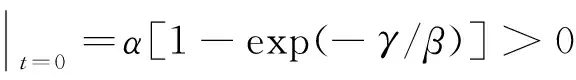
系统在[0,t]区间内的期望故障数,即累积故障强度函数为
α,β,γ>0,t≥0
(3)
1.2 模型特性
首先,对模型故障强度函数λ(t)求一阶导数得
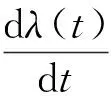
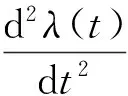
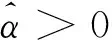
模型中参数α、β的意义如下:α为系统故障强度函数λ(t)的最大值,β为故障强度从初始强度增加到渐近值α所经历的时间,且其大小决定故障强度的初始增加速率,β值越小,故障强度增加的越快,直至增加到接近α值。
设单一系统在故障观察区间[0,T]的故障时间为t1,t2,…,tn,其中tn=T时为故障截尾试验,tn≠T时为时间截尾试验,则故障时间ti的条件概率密度函数为
f(ti|ti-1)=α[1-exp(-(ti+γ)/β)]·
exp{-α[(ti-ti-1)-β(exp(-(ti-1+γ)/β)-
exp(-(ti+γ)/β))]}
(4)
按照文献[9]中的理论,用w(t)表示系统在任意时刻t至下一次故障发生所需的时间,即w(t)=TN(t)+1-t,式中TN(t)+1为第N(t)+1个故障发生的时间,则

当t=0时,E{w0}与平均首次故障时间E{t1}相等,即有



exp(-(t+γ)/β))]}dt
(5)
下面证明故障间隔时间所服从的分布情况。
对于任意t≥0,有[1-exp(-t/β)]<1,所以
β[exp(-γ/β)-exp(-(t+γ)/β)]=
βexp(-γ/β)[1-exp(-t/β)]<βexp(-γ/β)
即
t-β[exp(-γ/β)-exp(-(t+γ)/β)]>
t-βexp(-γ/β)
因此得

exp[αβexp(-γ/β)]/α
从而可以得出,对于任意α,β,γ>0,E(t1)存在极限。相应地,对于t≥0,E(wt)存在极限[10]。
2 模型参数及可靠性指标的极大似然估计
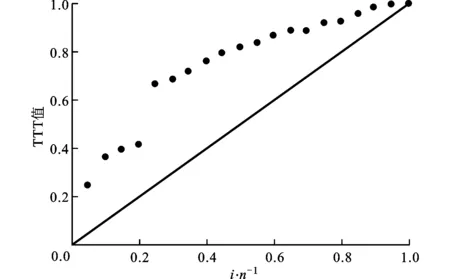
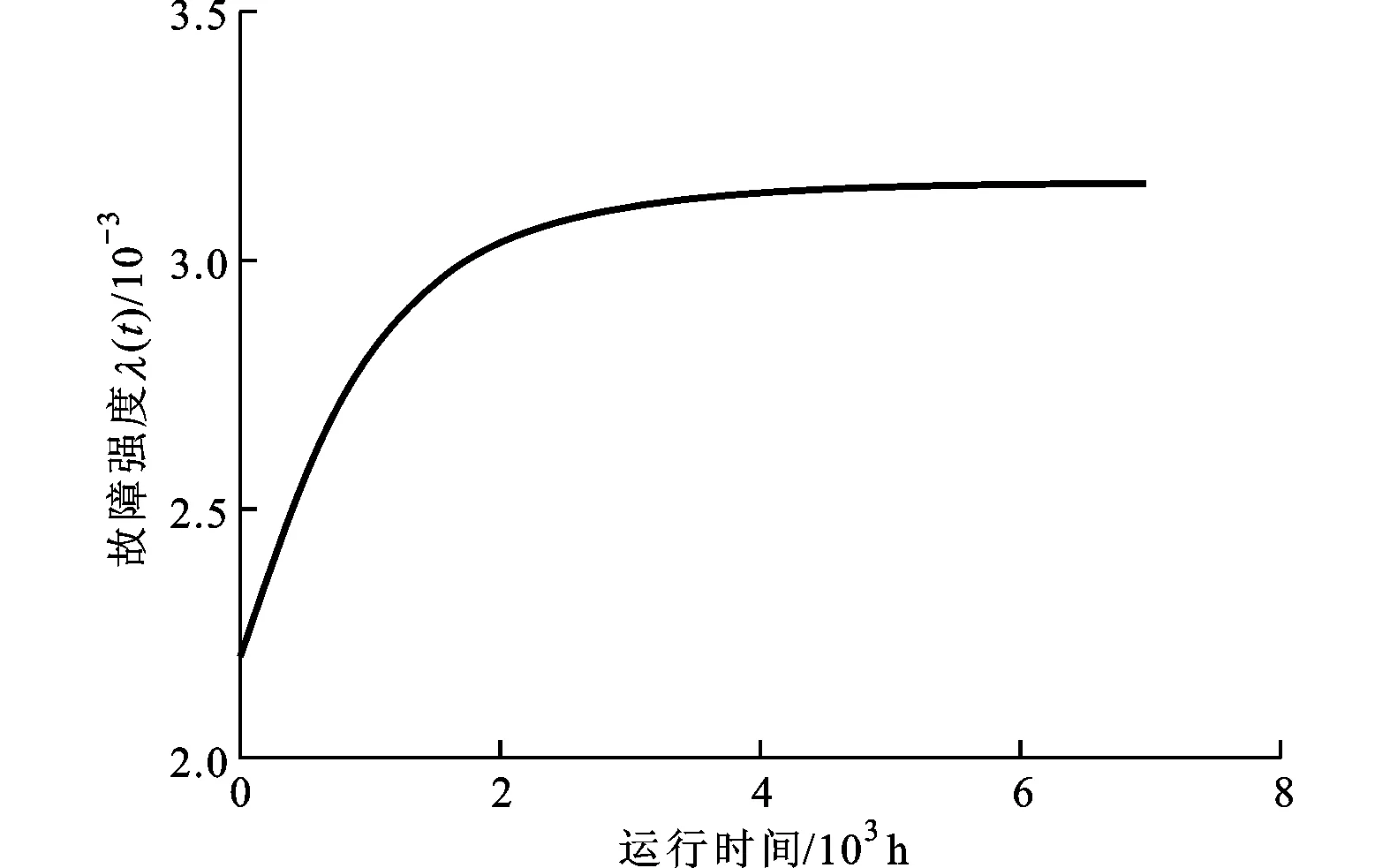
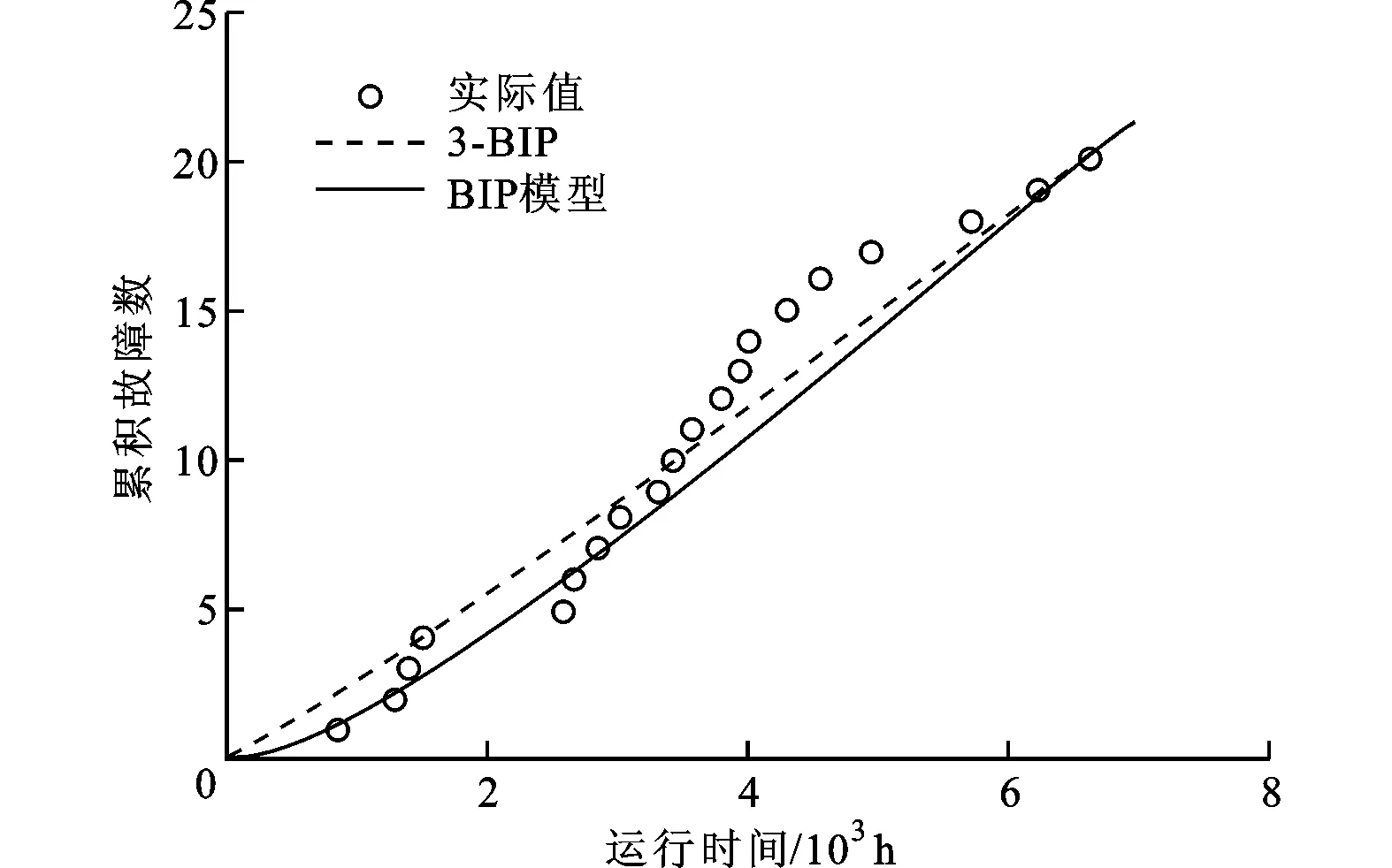
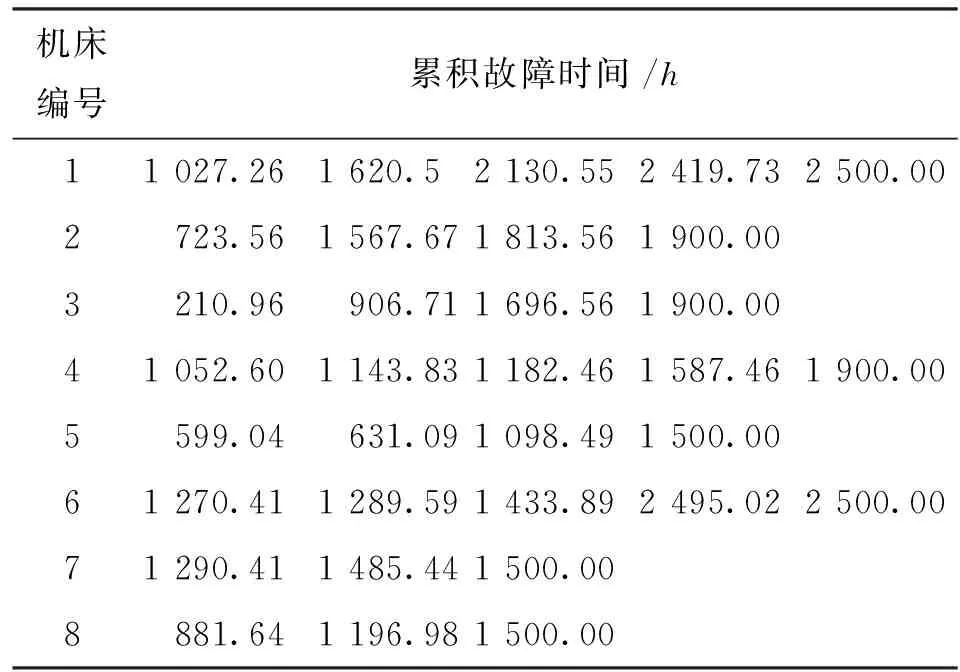
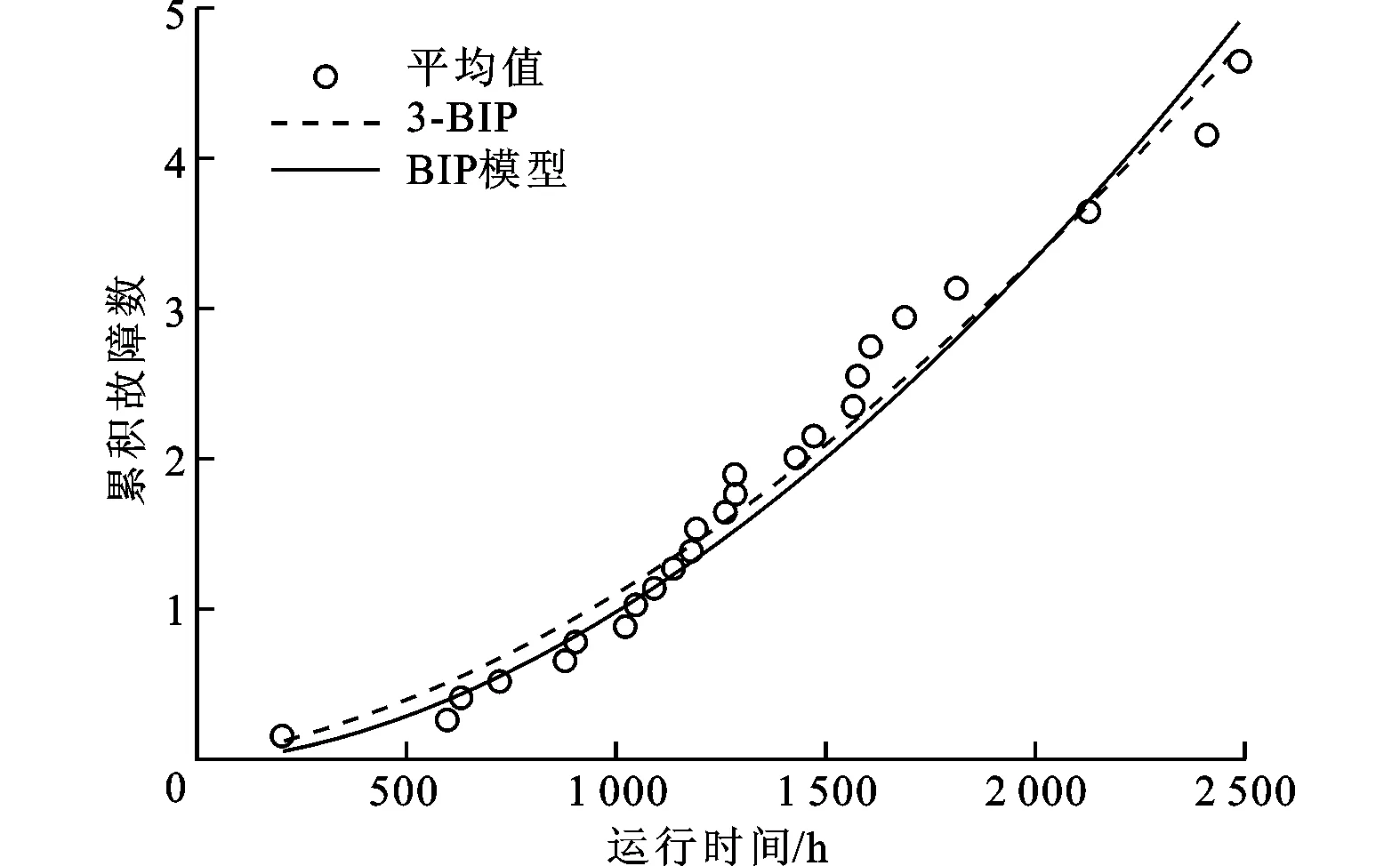
假定共有m台工作环境相近的同型数控机床,第j台机床在观测时间[0,Tj]发生了nj个故障,且第i个故障发生时间是tji(i=1,2,…,nj;j=1,2,…,m),按照时序的故障时刻为0 exp(-(ti+γ)/β)]}exp{-α[T-β(exp(-γ/β)- exp(-(T+γ)/β))]} (6) 对于故障截尾试验,只需令T=tn。 对于m台同型数控机床,其似然函数及对数似然函数分别为 exp(-(tj,i+γ)/β)]} (7) exp(-(Tj+γ)/β)]} (8) 对式(8)参数α求一阶偏导数,并令其为零,可得 (9) 将(9)式代入(8)式中可以得到一个含有两个参数的对数似然函数 exp(-(tj,i+γ)/β)]}-N (10) 累积故障强度M(t)、瞬时平均故障间隔时间tIMTBF、累积平均故障间隔时间tCMTBF及给定时刻的可靠度R(t)等可靠性指标的极大似然估计为 (11) (12) (13) (14) 实例1:对文献[11]中某一机床故障数据,通过求出早期故障期与偶然故障期转折点并进行转换,得到某机床厂一台加工中心的故障时间数据(单位为h)依次为:836.5,1 291.24,1 401.96,1 497.44,2 595.37,2 683.46,2 840.26,3 039.91,3 332.24,3 429.15,3 592.53,3 809.97,3 960.94,4 012.37,4 313.44,4 546.03,4 947.2,5 726.61,6 231.34,6 628.99。最后一个数据为故障截尾时间。 首先,按照TTT(total time on test)图检验方法[12],对上述加工中心故障数据进行趋势检验,结果如图1所示。图中i/n为第i个故障数与总故障数的比值,纵坐标为TTT值,具体计算方法见文献[12]。从图中可以看出,所有散点均分布在单位正方形对角线的上方,表明数控机床故障强度增大,正处于“耗损期”的阶段。 图1 加工中心故障截尾TTT图 另外,若采用威布尔过程模型建模,得模型参数b=1.329 2,也表明数控机床已进入损耗阶段。因此,可以采用本文提出的3-BIP模型对其进行可靠性分析。不同模型的计算结果如表1所示,由表中lnL值可以看出,3-BIP模型优于BIP模型,说明机床在数据采集初始时刻至少运行了1 123.72 h,且相应的故障强度λ0=0.002 169,说明机床初始时刻发生一次故障所需时间约为461 h,而BIP模型假设初始时刻发生一次故障的时间为无穷大,显然不合理,因此,3-BIP模型更符合工程实际。3-BIP模型的故障强度曲线如图2所示。 图2 3-BIP模型的故障强度曲线 为进一步验证3-BIP模型即为最佳模型,还需进行拟合优度检验。定义拟合优度评价指标[13]为 经计算,不同模型的拟合优度检验结果如表1所示,累积故障数拟合曲线如图3所示。显然,3-BIP模型的拟合效果优于BIP模型,说明在评估处于耗损期的数控机床可靠性时,考虑磨损、疲劳及老化等因素对信息采集初始时刻机床可靠性的影响是必要的。 图3 累积故障数拟合曲线 3-BIP模型和BIP模型可靠性指标的点估计结果如表2所示。从表中可以看出,机床运行至6 628.99 h时,3-BIP模型和BIP模型的累积平均故障间隔时间虽近似相等,但前者的平均可靠度低于后者,因此,若按BIP模型描述该数控机床的故障过程,可能会造成制定不合理的维修策略,从而影响企业生产效率。 实例2:文献[8]分别采用BIP模型及PLP模型分析了8台同型号数控机床(编号为1~8)一年的33个时间截尾故障数据,如表3所示。 表1 不同模型的计算结果 表2 3-BIP模型和BIP模型可靠性指标的点估计结果 表3 8台同型号数控机床的故障数据 文献[8]经计算证明,该8台同型数控机床已进入耗损阶段,因此,可以采用本文提出的3-BIP模型对上述数控机床故障过程进行分析。不同模型的计算结果如表4所示,累积故障数拟合曲线如图4所示,不难看出,3-BIP模型优于BIP模型。由表4说明机床在数据采集初始时刻已至少运行了193.49 h,且相应的故障强度λ0=3.42×10-4,表明故障信息采集初始时刻机床有突发故障的风险,但该值相对系统最大故障强度α=4.58×10-3稍小,这可能是因为机床刚刚进入耗损期,系统各零部件损伤的程度相对较小或机床刚刚经历过维修,及时更换了部分损伤零部件的缘故。 图4 累积故障数拟合曲线 表5给出了3-BIP模型和BIP模型可靠性指标的点估计结果,可以看出,在机床运行至2 500 h时,3-BIP模型的平均可靠性水平低于BIP模型的水平,因此,为优化使用机床,应以3-BIP模型给出的结果作为参考来制定维修策略。 表4 不同模型的计算结果 表5 3-BIP模型和BIP模型可靠性指标的点估计结果 对于处于耗损期的可修复系统,为更准确地描述其故障过程,本文在建模时考虑系统故障机理及维修等因素的影响,提出一种新的三参数边界强度过程模型。该模型是非齐次泊松过程模型的一种,其故障强度在零时刻为一常数,在系统工作时间较长时,有一渐近边界,更适合描述处于耗损期的可修系统故障过程。但是,由于位置参数的引入,增加了模型参数估计的难度,为此本文将参数估计问题转化为优化问题,给出了模型参数及重要可靠性指标的极大似然估计,并以2组数控机床现场故障数据为例,对模型进行了验证,结果均表明本文模型能够更加准确地评估数控机床的可靠性,从而可为合理地制定机床维修策略提供一定的理论参考。 [1] 康锐, 李瑞莹, 王乃超, 等. 可靠性与维修性工程概论 [M]. 北京: 清华大学出版社, 2010. [2] 张英芝, 申桂香, 薛玉霞, 等. 随机截尾数控机床故障过程 [J]. 吉林大学学报: 工学版, 2007, 37(6): 1346-1348. ZHANG Yingzhi, SHEN Guixiang, XUE Yuxia, et al. Failure process for numerical control machine with random ending method [J]. Journal of Jilin University: Engineering and Technology Edition, 2007, 37(6): 1346-1348. [3] MARSHALL S E, CHUKOVA S. On analyzing warranty data from repairable items [J]. Quality and Reliability Engineering International, 2010, 26(1): 43-52. [4] 王智明, 杨建国, 王国强, 等. 多台数控机床最小维修的可靠性评估 [J]. 哈尔滨工业大学学报, 2011, 43(7): 127-130. WANG Zhiming, YANG Jianguo, WANG Guoqiang, et al. Reliability assessment of multiple NC machine tools with minimal repair [J]. Journal of Harbin Institute of Technology, 2011, 43(7): 127-130. [5] WANG Z M, YU X. Log-linear process modeling for repairable systems with time trends and its applications in reliability assessment of numerically controlled machine tools [J]. Proceedings of the Institution of Mechanical Reliability Engineers: Part O Journal of Risk and Reliability, 2013, 227: 55-65. [6] ASCHER H, FEINGOLD H. Repairable systems reliability: modeling, misconceptions and their causes [M]. New York, USA: Marcel Dekker, 1984. [7] PULCINI G. A bounded intensity process for the reliability of repairable equipment [J]. Journal of Quality Technology, 2001, 33(4): 480-492. [8] 王智明, 杨建国. 数控机床可靠性评估中的边界强度过程 [J]. 上海交通大学学报, 2012, 30(10): 1622-1626. WANG Zhiming, YANG Jianguo. Bounded intensity process and its applications in reliability assessment of NC machine tools [J]. Journal of Shanghai Jiaotong University, 2012, 30(10): 1622-1626. [9] THOMPSON W A. On the foundation of reliability [J]. Technometrics, 1981, 23(1): 1-13. [10]ENGELLHARDT M, BAIN L J. On the mean time between failures for repairable systems [J]. IEEE Transactions on Reliability, 1986, 35(4): 419-422. [11]许彬彬, 杨兆军, 陈菲, 等. 非齐次泊松过程的数控机床可靠性建模 [J]. 吉林大学学报: 工学版, 2011, 41(S2): 210-214. XU Binbin, YANG Zhaojun, CHEN Fei, et al. Reliability model of CNC machine tools based on non-homogeneous Poisson process [J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(S2): 210-214. [12]LOUIT D M, PASCUAL R, JARDINE A K S. A practical procedure for the selection of time-to-failure models based on the assessment of trends in maintenance data [J]. Reliability Engineering and System Safety, 2009(94): 1618-1628. [13]舒继森, 郭兵兵, 张俊阳, 等. 基于拟合优度指标评价的岩土参数概率分布研究 [J]. 采矿与安全工程学报, 2008, 25(2): 197-201. SHU Jisen, GUO Bingbing, ZHANG Junyang, et al. Research on probability distribution of parameters of rock and soil based on fitting optimization index [J]. Journal of Mining & Safety Engineering, 2008, 25(2): 197-201. [本刊相关文献链接] 杨军,施虎,梅雪松,等.双驱伺服进给系统热误差的试验测量与预测模型构建.2013,47(11):53-59.[doi:10.7652/xjtuxb201311010] 冯斌,梅雪松,杨军,等.数控机床摩擦误差自适应补偿方法研究.2013,47(11):65-69.[doi:10.7652/xjtuxb201311012] 陈晓光,徐光华,梁霖,等.一种电流弱信号特征提取方法.2013,47(9):83-87.[doi:10.7652/xjtuxb201309014] 赵飞,梅雪松,姜歌东,等.数控机床进给系统模态参数的自激振辨识方法.2013,47(5):88-92.[doi:10.7652/xjtuxb 201305016] 李学伟,赵万华,卢秉恒.轨迹误差建模的多轴联动机床轮廓误差补偿技术.2012,46(3):47-52.[doi:10.7652/xjtuxb 201203009] 吴沁,芮执元,杨建军.考虑非线性弹性力的滚珠丝杠系统分岔与混沌特性分析.2012,46(1):70-75.[doi:10.7652/xjtuxb201201013] 蔡改改,陈雪峰,陈保家,等.利用设备响应状态信息的运行可靠性评估.2012,46(1):108-113.[doi:10.7652/xjtuxb2012 01020] (编辑 赵炜) Three-ParameterBoundedIntensityProcessModelandItsApplicationinReliabilityAssessmentofNCMachineTools REN Lina1,2,RUI zhiyuan1,LI Jianhua1,LI Haiyan1 (1. School of Mechanical and Electronic Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. School of Mechatronics Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China) To improve the reliability assessment accuracy of NC machine tools, a three-parameter bounded intensity process (3-BIP) model by intensity function with non-zero initial condition is proposed. The characteristic of the model is confirmed by differentiating with respect to the failure intensity function, and the relationship between the three-parameter bounded intensity process and the homogenous Poisson process is derived. The calculating formula for model parameters and reliability indexes are deduced by the maximum likelihood estimation and optimization. Two examples of the failure truncated data from single NC machine tool and the time truncated data from multiple NC machine tools are taken respectively to verify the proposed method. The results of log-likelihood function and goodness-of-fit show that the 3-BIP model is better than the BIP model, so the 3-BIP model accords with practical engineering well and provides a theoretical basis for making a reasonable maintenance strategy. three-parameter bounded intensity process; maximum likelihood estimation; NC machine tool; reliability assessment 10.7652/xjtuxb201405019 2013-09-13。 作者简介: 任丽娜(1981—),女,讲师,电子科技大学博士生;李建华(通信作者),男,副教授,博士。基金项目: 国家重大数控专项资助项目(2010ZX04001-032);国家自然科学基金资助项目(51165018)。 TG659;TB114 :A :0253-987X(2014)05-0107-06
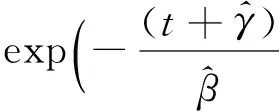
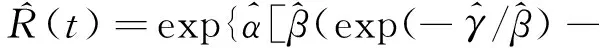
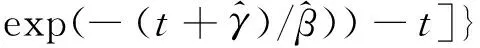
3 模型应用




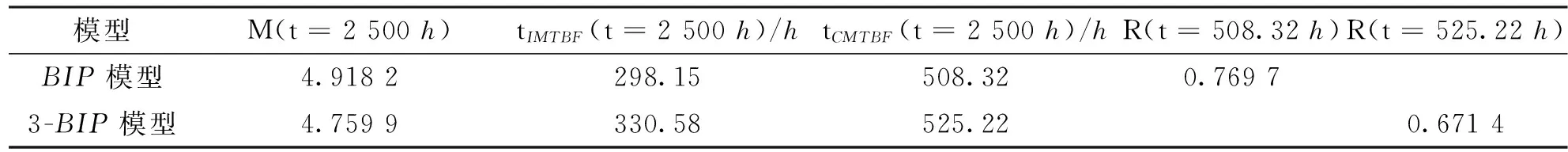
4 结 论

