高瑞利数下封闭腔内自然对流的数值模拟

阳祥,陶文铨

(1.国家核电技术有限公司北京研发中心, 100190, 北京; 2.西安交通大学能源与动力工程学院, 710049, 西安)

高瑞利数下封闭腔内自然对流的数值模拟

阳祥1,陶文铨2

(1.国家核电技术有限公司北京研发中心, 100190, 北京; 2.西安交通大学能源与动力工程学院, 710049, 西安)

为了推广应用高瑞利数下的自然对流换热技术,有必要对自然对流流动与换热特性进行深入研究。采用不引入人工扰动的直接数值模拟方法,对发生在高宽比为4的封闭腔内的自然对流流动与换热进行了研究,分析了平均温度、平均主流速度、涡量和局部努塞尔数的分布特性。研究结果表明:从静止等温流体初始条件出发,不引入任何人工扰动自然对流可以顺利发展到湍流,节约了计算资源;即便瑞利数等于1010,自然对流的平均温度、平均主流速度、涡量和局部努赛尔数分布都具有边界层型流动和换热的特征;在普朗特数为0.71～500的范围,当封闭腔内自然对流换热出现湍流换热特征时,局部瑞利数处于107～108量级。

封闭腔;湍流;自然对流;直接数值模拟

竖直封闭腔内的自然对流是传热与流动学科中的一个经典问题,有很多工程应用背景,如核反应堆中的换热、放射性废料的冷却、房间通风、太阳能集热器和电子器件冷却等。竖直壁面存在温差的封闭腔内沿高温、低温竖直壁面会分别形成上升流动和下降流动,并且在腔内形成回流,高瑞利数Ra流动会形成层流、过渡和湍流区域。Tian和Karayiannis对弱湍流自然对流进行了实验研究,首次发表了加热封闭腔内温度等值线分布和速度矢量分布的实验结果[1-2]。Giel等对几种高宽比的封闭腔内自然对流传热(高Ra)进行了试验研究,测量了速度和温度的平均值和脉动值分布,并进一步获得了脉动速度和温度的频谱图;在分析试验结果的基础上他们认为高宽比大于等于4的封闭腔内发生湍流自然对流时展向的尺寸大小对流动和换热影响很小[3]。在数值模拟方面的研究要少得多,尤其是直接模拟和大涡模拟的研究更少,竖直壁面自然对流通常在高Ra下才会转变为湍流,并且从层流过渡到湍流很难处理,对计算技术和资源要求很高。Paolucci首次对竖直壁面存在温差的方腔自然对流问题进行直接模拟,他采用有限差分法对二维封闭方腔内湍流自然对流进行了模拟,证实了自然对流从层流到湍流直接模拟的可行性[4]。Trias等采用直接数值模拟方法研究了高Ra下二维封闭腔和三维封闭腔的自然对流,结果表明二维和三维计算在模拟封闭腔内自然对流和换热的一般特征时基本没有差别,二维计算更为经济实用,三维计算具有更丰富的信息,特别是在湍流高阶统计量方面[5]。

本文对几种物质(不同普朗特数Pr)在高宽比为4的封闭腔内发生的自然对流采用经济实用的二维直接数值模拟,分析了包括速度场、温度场、涡量场和局部努塞尔数Nuy分布的特点,揭示了自然对流从层流到湍流的流动与换热特性。

1 物理模型和数学模型

1.1 物理模型

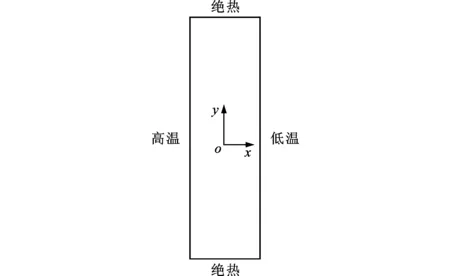
图1 物理模型示意图

本文采用如图1所示的物理模型,x坐标轴沿水平方向,y坐标轴沿竖直方向,坐标原点在二维封闭腔的中心,方腔高宽比为4,水平壁面绝热,两竖直壁面温度分别保持恒定,并且左壁面温度高右壁面温度低。

1.2 数学模型

采用Boussinesq假设,归一化的二维质量守恒方程、动量守恒方程和能量守恒方程如下

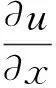
(1)

(2)

RaPrΘ

(3)

(4)

1.3 控制方程的离散及数值方法

采用分步算法求解非稳态N-S方程,采用有限差分法离散控制方程,对流项和扩散项都采用二阶相容中心差分格式,在时间离散上采用二阶半隐半显的混合Adams-Bashforth/Crank-Nicholson格式。

湍流自然对流的直接数值模拟需要满足空间和时间尺度要求。根据George等给出的经验公式[6]来估算自然对流中的导热次层厚度,如下式所示

λ≈1.7(PrRam)-1/3

(5)

式中:Ram是基于ΔTm=Th-T0定义的,其中T0=0.5(Th+Tc)。时间尺度也应满足一定的要求,根据Paolucci的经验[3],时间尺度满足下式要求

Δt≤8π(Ra3Pr)-1/4

(6)

按照上述要求,本文中选取的网格数沿x和y方向分别为160×320,x方向的最大网格距离为9.8×10-3,y方向最大网格距离为1.96×10-2,最小网格距离在贴近壁面处,沿竖直壁面和水平壁面的最小网格距离均为1×10-5,选取的时间步长为Δt=1×10-8。

速度采用无滑移边界条件,高温壁面的温度边界条件为Θ=0.5,低温壁面为Θ=-0.5,水平壁面上绝热。计算初场为0,为了得到统计解,在完全进入湍流状态后,再进行至少200万步左右的时间推进,每隔1万步进行数据采集,对采集到的瞬时数据进行时间平均,得到统计解。在数据处理中首先完成了数值结果对网格数量的依赖性,文中展示的计算数据都是完成网格无关性考核后的结果。

1.4 程序验证

图2 边界层外区域归一化主流速度分布

2 计算结果及分析

2.1 流场和温度场

图3给出了不同Pr下的等温线分布,由图可知等温线的拓扑结构关于x=0反对称。沿着竖直高温壁面流体朝上呈边界层型流动,在底部区域温度在很薄的流体层内变化,超过封闭腔一半高度后等温线明显朝上凸出,温度边界层明显增厚,自然对流失稳并进入湍流状态。低温壁面侧流体的温度变化与高温侧相似,但是方向发生了变化。在封闭腔的中心区域内等温线沿x方向的变化较小,随着Pr增加沿水平方向温度变化满足∂Θ/∂x≈0,流体呈明显的分层状态。这是因为随着Pr增加,流体黏滞作用相对增强,温度边界层减薄的缘故。

图4给出了平均主流速度V和平均温度Θ沿y=0的分布,V和Θ关于x=0反对称,文中只给出高温侧的温度和速度分布。在y<0的区域内自然对流已经完成从层流到湍流的过渡,因此图中的速度和温度分布都是湍流状态下的。从图4a可看出,速度分布定性上与竖直平板自然对流的速度分布相似:当-0.5-0.35时主流速度几乎为0。图4b中是平均温度的分布,温度在-0.5-0.46时温度已降至0。比较图4b与图4a可知,温度边界层厚度明显小于速度边界层厚度。

图5是某一时刻封闭腔内自然对流的涡量分布,涡量的定义为ω=∂v/∂x-∂u/∂y,图中深色表示涡量大,浅色表示涡量小。涡量的分布展现了在浮升力驱动下流体运动沿竖直壁面的发展轨迹,下面以高温壁面(每幅图的左侧壁面)流动为例进行说明。在高温表面下部,涡量分布很规律,流动处于层流状态;靠近中间高度处,涡量分布变化较剧烈,流体呈抛射状向上运动,流动已经失稳伴有湍流的特征;超过中间高度后有明显的间歇性涡结构出现,涡量变化剧烈,表现出明显的湍流特征,流动已发展成旺盛的湍流;在靠近顶部的区域,由于上顶面的阻挡作用,涡量变化较剧烈,流体的脉动性减弱。在低温壁面,边界层型流动向下发展,壁面附近流体的涡量分布特性与高温壁面侧相似。随着Pr的变化,涡尺度发生了较明显的变化:Pr=0.71时湍流边界层内的涡尺度较大,可以清楚地观察到流体边界层在空间的演变,在左右两个流动边界层交汇的地方流体边界层之间发生了轻微的干涉;当Pr≥10时,涡尺度明显变小且呈长条状,数量增多,但流动边界层从层流到湍流的发展过程仍清晰可辨,涡量在中心区域内较弱,流体处于分层状态。

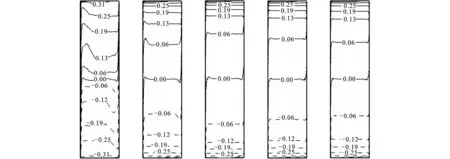
(a)Pr=0.71(b)Pr=10(c)Pr=50(d)Pr=100 (e)Pr=500

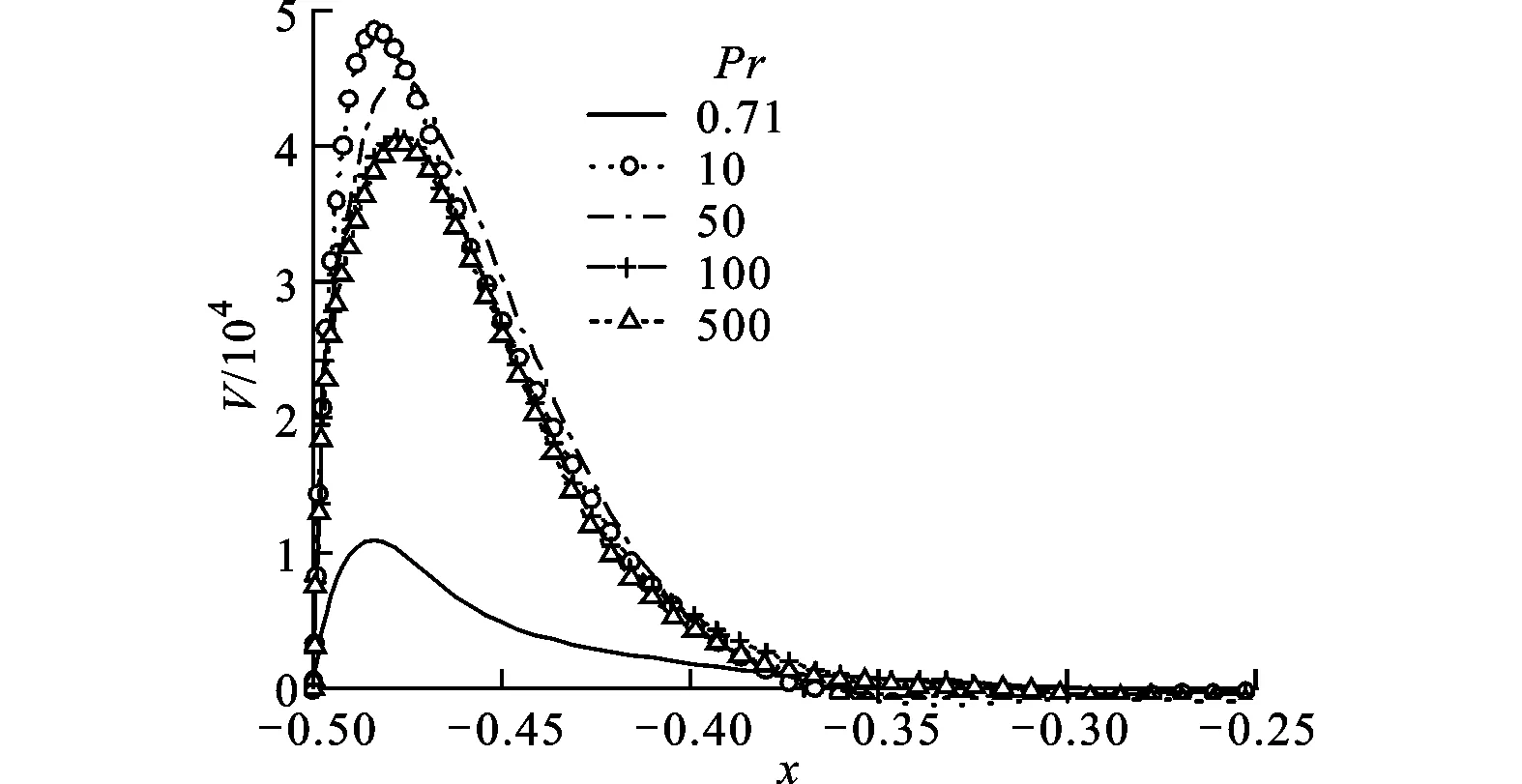
(a)V沿y=0水平线的分布

(b)Θ沿y=0水平线的分布

2.2 传热特性

图6展示了沿高温壁面局部努塞尔数Nuy随局部瑞利数Ray的变化曲线,Nuy定义为Nuy=hy/k,Ray定义为Ray=gβΔTy3/αν。由图可知,每条Nuy-Ray曲线都由层流区、过渡区、旺盛湍流区、顶部区4个区间组成。图6a给出了Pr=0.71时Nuy随Ray的变化情况,从高温壁面的底部起的一段区域内,流动为层流状态,Nuy呈线性下降;流动发展到过渡状态后,Nuy曲线发生振荡但频率较低、幅度较小;随着流动发展到旺盛湍流,Nuy曲线出现明显的高频次振荡;随着高度的进一步增加,壁面阻挡作用开始显现,流体脉动减弱,Nuy曲线又重新回归到接近直线分布,并且Nuy值急剧下降。随着Pr的增加,Nuy曲线振荡的幅值和频率都有所下降,这是因为黏滞作用相对增加了;在接近上壁面区域内,Nuy值下降得更快,并有层流化趋势。

根据Nuy-Ray曲线的分布特点,发现了一个非常有意思的现象:在Pr=0.71～500的范围内,Nuy都在Ray=107～108这个范围内开始发生振荡,此Ray范围对应的高度与温度、速度和涡量分布图中出现湍流特征的高度是一致的。因此,通过观察Nuy-Ray曲线,可以粗略地判断在Ray=107～108范围内,自然对流换热具有湍流换热的特点。

(a)Pr=0.71 (b)Pr=10(c)Pr=50(d)Pr=100 (e)Pr=500

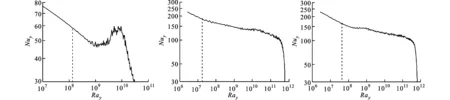
(a)Pr=0.71 (b)Pr=10 (c)Pr=50

(d)Pr=100 (e)Pr=500

3 结 论

本文对高宽比为4的封闭腔内自然对流进行了直接数值模拟,研究了自然对流从层流到湍流的流动与传热特性,得出以下结论:

(1)实现了从静止等温流体初始条件出发,在不引入任何人工扰动的情况下完成了封闭腔内自然对流的直接数值模拟,大大缩短了计算时间,节约了计算资源;

(2)封闭腔内自然对流的主要物理量沿等温壁面的分布,包括平均温度、平均主流速度、涡量和局部努赛尔数,具有边界层型流动和换热的特点,这些物理量的分布都展示了封闭腔内自然对流从层流到湍流的发展演变过程;

(3)不同Pr下封闭腔内自然对流换热有一定的共性,在Pr=0.71～500的范围内,当Ray=107～108量级时,自然对流换热具有明显的湍流换热特征。

[1] TIAN Y S, KARAYIANNIS T G. Low turbulence natural convection in an air filled square cavity: Part I The thermal and fluid flow fields [J]. International Journal of Heat and Mass Transfer, 2000, 43(6): 849-866.

[2] TIAN Y S, KARAYIANNIS T G. Low turbulence natural convection in an air filled square cavity: Part II The turbulence quantities [J]. International Journal of Heat and Mass Transfer, 2000, 43(6): 867-884.

[3] GIEL P, SCHMIDT F. An experimental study of high Rayleigh natural convection in an enclosure [C]∥Proceedings of the 8th International Heat Transfer Conference. San Francisco, USA: Hemisphere Publishing Corporation, 1986: 1459-1464.

[4] PAOLUCCI S. Direct numerical simulation of two-dimensional turbulent natural convection in an enclosed cavity [J]. Journal of Fluid Mechanics, 1990, 215: 229-262.

[5] TRIAS F X, SORIA M, OLIVA A. Direct numerical simulations of two-and three-dimensional turbulent natural convection flows in a differentially heated cavity of aspect ratio 4 [J]. J Fluid Mech, 2007, 586(3): 259-293.

[6] GEORGE W K. A theory for natural convection turbulent boundary layers next to heated vertical surfaces [J]. International Journal of Heat and Mass Transfer, 1979, 22(6): 813-826.

[7] FARHANGNIA M, BIRINGEN S, PELTIER L J. Numerical simulation of two-dimensional buoyancy-driven turbulence in a tall rectangular cavity [J]. International Journal for Numerical Methods in Fluids, 1998, 23(12): 1311-1326.

(编辑 荆树蓉)

NumericalSimulationsforNaturalConvectionwithHighRayleighNumberinaTallRectangularCavity

YANG Xiang1,TAO Wenquan2

(1. Beijing R&D Center of State Nuclear Power Technology Corporation, Beijing 100190, China;2. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To generalize heat transfer technology of natural convection with high Rayleigh number, it is necessary to extensively investigate the characteristics of fluid flow and heat transfer by natural convection. For a tall rectangular cavity of an aspect ratio 4, direct numerical simulations are carried out without any artificial perturbations on the flow field, and the distributions of averaged physical quantities such as temperature, mainstream velocity, vorticity and local Nusselt number are analyzed. The results show that: 1) Starting under quiescent and isothermal flow conditions, the flow can be driven to turbulence without any artificial perturbations, which saves computational resources; 2) As Rayleigh numbers up to 1010, the distributions of temperature, mainstream velocity, vorticity and local Nusselt numbers for natural convection in the tall cavity are endowed with the similar features of those in boundary-layer flow on a heated vertical plate; and 3) With Prandtl number in range of 0.71-500 and local Rayleigh number of magnitudes 107-108, heat transfer on the isothermal surfaces of tall cavity already presents the characteristics of turbulent flow.

enclosure; turbulence; natural convection; direct numerical simulation

10.7652/xjtuxb201405005

2013-08-21。 作者简介: 阳祥(1980—),男,工程师。 基金项目: 国家自然科学基金重点资助项目(51136004)。

时间: 2014-02-26 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140226.1203.031.html

TK124

:A

:0253-987X(2014)05-0027-05