四次拟Bézier旋转曲面的构造技术

胡钢,宋伟杰

(1.西安理工大学理学院,710054,西安; 2.西北工业大学理学院,710072,西安)

四次拟Bézier旋转曲面的构造技术

胡钢1,宋伟杰2

(1.西安理工大学理学院,710054,西安; 2.西北工业大学理学院,710072,西安)

为了方便解决传统旋转曲面计算复杂和形状难以调节的问题,研究了一种带多形状参数的四次拟Bézier旋转曲面的构造技术。首先,基于二元超限向量值有理插值函数的重要思想,利用带多形状参数的四次拟Bézier曲线作为母线进行旋转曲面的设计;其次,推导了生成整个四次拟旋转曲面的一个显式函数表达式。该方法生成的旋转曲面不仅计算简单而且具有良好的形状可调性,同时还保留了传统Bézier旋转曲面的许多几何特性。最后,对所设计的旋转曲面进行了形状与性质分析,并给出了形状控制参数对旋转曲面形状的影响规律。造型实例表明,所提方法不仅直观、高效,而且易于调整旋转曲面的局部形状,在各种旋转曲面的构造与外形设计中将得到十分广泛的应用。

四次拟Bézier曲线;形状参数;旋转曲面;超限向量值有理插值函数

Bézier曲线由于具有许多优良的特性,如今已成为CAD/CAM领域用于描述产品形状信息的主要方法之一。近年来,为了弥补Bézier曲线曲面造型技术的缺点,人们另辟新径,构造了许多非有理形式的带形状参数的Bézier曲线[1-10]。其中,四次拟Bézier曲线作为一种新颖的曲线造型方法[9-10],不仅保留了传统Bézier曲线的所有优点,同时具有计算复杂度较低和形状灵活可调的特点,所以该曲线在CAD/CAM领域中将得到广泛的应用[9-10]。

为了增强四次拟Bézier曲线的造型能力,人们继续研究了该曲线的一些关键技术,如拼接技术[9]、形状修改[10]等。然而,在航天航空、机械加工、工业产品设计以及3D动画设计等领域会经常遇到旋转曲面的快速生成问题,在现有的CAD系统中通常将旋转曲面表示为Bézier的参数形式,所以研究Bézier旋转曲面的构造技术无疑具有重要理论价值和实际意义。

生成旋转曲面的常用方法一般有基于三维坐标变换法[11]、B样条曲线理论[12]、散乱数据三角剖分[13]以及轮廓约束的旋转曲面绘制[14]等。上述方法生成的旋转曲面存在如下2个缺点:①形状可调性有限,即没有考虑旋转曲面局部或整体的形状调整问题,一旦旋转曲面生成,若要修改其形状需要重新设计旋转曲面,操作麻烦且费时、费力,无法更好地满足实际需要;②缺乏显式函数表达式,且计算复杂度较高。

为此,本文基于超限向量值有理插值函数的重要思想,利用带多参数的四次拟Bézier曲线,研究了一种带多形状参数的四次拟Bézier旋转曲面的几何构造问题。所提方法不仅能够快速、简便地生成任意旋转式曲面,而且可以对所生成的旋转曲面进行整体(或局部)形状调整,较好地解决了旋转曲面形状难以调节的问题。

1 四次拟Bézier曲线

四次带参Bézier曲线[6-8]虽然继承了Bézier方法几何上的一些优良性质,且形状参数可调,但由于只含单个形状参数使得其形状可调性有限。为此,文献[10]在四次带参Bézier曲线的基础上给出四次拟Bézier曲线的概念。

若给定4个控制顶点向量Pj∈Rd(d=2,3;j=0,1,2,3),四次拟Bézier曲线定义如下[10]

(1)

式中:0≤t≤1,λ、μ∈[-3,1]称为形状参数;四次基函数bj,4(t)(j=0,1,2,3)为

(2)

显然,当λ=μ时,式(1)便退化为文献[6-8]中的四次带参Bézier曲线,这表明该曲线是四次拟Bézier曲线的一个特例。不难证明,四次拟Bézier曲线同样具有端点性质、凸包性以及几何不变性等几何性质。此外,形状参数λ、μ对四次拟Bézier曲线形状的影响规律也十分明显,即为:①不改变μ值,将λ的值慢慢变小(或变大),曲线会慢慢远离(或靠近)它的控制顶点P1;②不改变λ的值,将μ的值慢慢变小(或变大),曲线会慢慢远离(或靠近)它的控制顶点P2;③λ、μ的值同时慢慢变小(或变大),曲线会慢慢远离(或靠近)其控制多边形。

类似于传统曲线的光滑拼接,可以推导四次拟Bézier曲线间G1、C1连续的充要条件。

定理1相邻2段四次拟Bézier曲线P(t;λ1,μ1)和Q(t;λ2,μ2)间G1连续的充要条件为

(3)

式中:α>0为任意常数;Pi和Qi(i=0,1,2,3)分别为P(t;λ1,μ1)和Q(t;λ2,μ2)的控制顶点。

显然,若假设式(3)中α=1,则曲线G1连续的充要条件退化为曲线C1连续的充要条件。四次拟Bézier曲线间光滑拼接的一个显著优点是:不用修改曲线G1、C1连续的条件,仅通过修改形状参数(无需调整控制顶点的位置)就可修改拼接后曲线的局部形状。

2 超限向量值有理插值函数

对于给定的d维复向量V∈Cd,它的Samelson逆定义为[15]

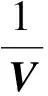
(4)

式中:V*为V的共轭向量;‖V‖为向量V的模。

根据式(4)中向量的Samelson逆,给出如下形式的二元超限向量值有理插值函数[15]

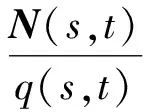
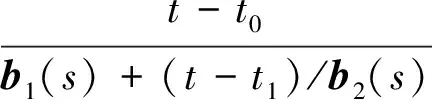
(5)

其满足如下的插值条件

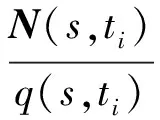
(6)

式中:N(s,t)={λ1(s,t),λ2(s,t),λ3(s,t)}是三维向量值函数,而λj(s,t)(j=0,1,2)和q(s,t)都是变量s、t的实函数;Vi(s)、bi(s)(i=0,1,2)都是s的三维向量值函数;ti(i=0,1,2)是实常数。

3 四次拟Bézier旋转曲面的构造

3.1 算法的描述

本节讨论如何利用二元超限向量值有理插值函数的思想,结合一条分段的四次拟Bézier曲线给出一种旋转曲面构造算法,可以快速生成空间任意形状的旋转曲面。下面给出算法的基本步骤。

步骤1在空间直角坐标系的xoy平面(其他平面可类似讨论)上,首先构造一条以Pi,0、Pi,1、Pi,2、Pi,3(i=1,2,…,n)为控制顶点的分段组合四次拟Bézier曲线S0,并将S0写成向量的形式为

Vi,0(s;λi,μi)={xi,0(s),yi,0(s),0}

i=1,2,…,n

(7)

式中:Vi,0(s;λi,μi)按式(1)定义,它表示四次拟Bézier曲线S0的第i段曲线,其控制顶点为Pi,0、Pi,1、Pi,2、Pi,3;λi、μi为形状参数。曲线S0的相邻两段Vi,0(s;λi,μi)和Vi+1,0(s;λi+1,μi+1)间通常要达到G0、G1或C1连续。

其次,在xoz平面(其垂直于xoy平面)上作曲线S1,写成向量函数形式为

Vi,1(s;λi,μi)={xi,1(s),0,zi,1(s)}=

{xi,0(s),0,yi,0(s)},i=1,2,…,n

(8)

式中:Vi,1(s;λi,μi)表示曲线S1的第i段,该曲线段是由曲线S0的第i段Vi,0(s;λiμi)绕着x轴顺时针旋转90°得到的。

最后,以x轴为对称轴L,在xoy平面上作曲线S0关于L对称的曲线S2,记为

Vi,2(s;λi,μi)={xi,2(s),yi,2(s),0}=

{xi,0(s),yi,0(s),0},i=1,2,…,n

(9)

式中:Vi,2(s;λi,μi)表示曲线S2的第i段。从而,得到位于2块相互垂直平面(xoy平面和xoz平面)上的3条参数曲线如下

(10)

步骤2将曲线Vi,0(s;λi,μi)、Vi,1(s;λi,μi)和Vi,2(s;λi,μi)作为3个插值条件函数,可构造形如式(5)的超限向量值有理插值函数,步骤如下。

(1)令t0=0,t1=0.5,t2=1,并定义向量函数

bi,0(s;λi,μi)=Vi,0(s;λi,μi),i=1,2,…,n

(11)

(2)由向量Samelson逆的定义,令

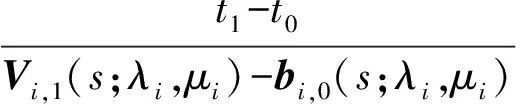
并将Ri,1(s,t1;λi,μi)记为

bi,1(s;λi,μi)=Ri,1(s,t1;λi,μi),i=1,2,…,n

(12)

(3)分别定义

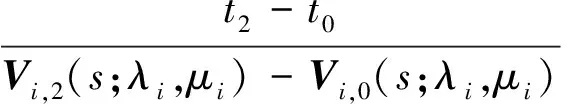
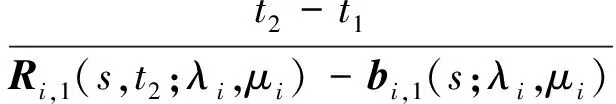
并将Ri,2(s,t2;λi,μi)记为

(13)

(4)将bi,j(s;λi,μi)(j=0,1,2;i=1,2,…,n)代入式(5),即可得

(14)

且满足如下插值条件Ri(s,tj;λi,μi)=Vi,j(s;λi,μi)

j=0,1,2;i=1,2,…,n

(15)

步骤3对函数Ri(s,t;λi,μi)进行由后向前的有理化,可以得到该函数的显式表达式

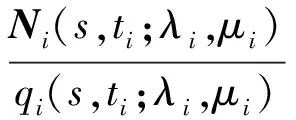
{ri,1(s,t;λi,μi),ri,2(s,t;λi,μi),ri,3(s,t;λi,μi)}

(16)

式中ri,1(s,t;λi,μi)=xi,0(s)

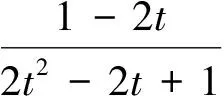
由文献[16]中的结论易证明,式(16)所表示的曲面是以参数曲线S0为母线的旋转曲面的一半(证明过程这里不再赘述)。

步骤4为了生成一个完整的旋转曲面,还需要进一步将Ri(s,t;λi,μi)(i=1,2,…,n)中的分量ri,3(s,t;λi,μi)取反号,即可生成剩余一半的旋转曲面,记为

{ri,1(s,t;λi,μi),ri,2(s,t;λi,μi),-ri,3(s,t;λi,μi)}

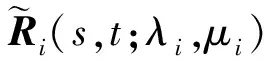
3.2 旋转曲面的性质

本节讨论四次拟Bézier旋转曲面继承的四次拟Bézier曲线的许多相关基本性质。

性质1边界插值性质。由四次拟Bézier曲线的端点性质可知,旋转曲面母线S0的每一段曲线Vi,0(s;λi,μi)(i=1,2,…,n)均插值它的始末控制顶点Pi,0、Pi,3,且Vi,0(s;λi,μi)和Vi+1,0(s;λi+1,μi+1)的控制顶点满足Pi,3=Pi+1,0(i=1,2,…,n-1)。从而,四次拟Bézier旋转曲面会插值于由控制顶点Pi,0、Pi,3(i=1,2,…,n)分别绕着x轴旋转一周生成的n+1个圆。

性质2凸包性。四次拟Bézier旋转曲面位于一个空间的立体凸包之中,该空间立体凸包是由母线S0的凸包(凸包由母线的控制顶点生成)绕着x轴旋转一周生成的。

性质3光滑性。如果旋转曲面的母线S0满足每相邻2段Vi,0(s;λi,μi)和Vi+1,0(s;λi+1,μi+1)间要达到G0、G1或C1光滑拼接,则旋转曲面沿其母线方向也必然达到G0、G1或C1光滑拼接。

性质4逼近性。当λ、μ同时逐渐增大时,四次拟Bézier曲线逐渐逼近它的控制多边形。所以,随着参数λi、μi同时逐渐增大,四次拟Bézier旋转曲面会逐渐地逼近由其母线S0的控制多边形绕x轴旋转一周生成的旋转曲面。

3.3 形状参数对旋转曲面形状的影响规律

旋转曲面中形状参数的影响规律为:①当μi保持不变,λi慢慢变小或变大时,Ri(s,t;λi,μi)逐渐地远离或靠近由母线控制顶点Pi,1绕x轴旋转一周生成的圆;②当λi保持不变,随着μi慢慢地变小或变大,Ri(s,t;λi,μi)会慢慢远离或靠近其母线的控制顶点Pi,2绕x轴旋转一周生成的圆;③当形状参数λi、μi同时逐渐地变小或变大时,旋转曲面Ri(s,t;λi,μi)逐渐地远离或靠近由母线S0的控制多边形绕x轴旋转一周生成的控制旋转曲面。

4 数值实例

实例1:给定xoy平面上的8个控制顶点,生成2段四次拟Bézier曲线Vi,0(s;λi,μi)(i=1,2),试求以Vi,0(s;λi,μi)为母线,绕x轴旋转一周生成的旋转曲面。这里,母线的控制顶点坐标为

(17)

解:由式(1)可知,以Pi,j(i=1,2;j=0,1,2,3)为控制顶点生成的母线Vi,0(s;λi,μi)(i=1,2)的参数方程为

Vi,0(s;λi,μi)={xi,0(s),yi,0(s),0},i=1,2

(18)

式中

x1,0(s)=(15+5λ1)s-(15+15λ1)s2+

(10+15λ1-5μ1)s3-(5λ1-5μ1)s3

y1,0(s)=5+(15+5λ1)s+(3-15λ1)s2-

(3-15λ1+4μ1)s3-(5λ1-4μ1)s4

x2,0(s)=10+(30+10λ2)s-30λ2s2+

(30λ2-10μ2)s3-(10λ2-10μ2)s4

y2,0(s)=20-(15+5λ2)s-(15-15λ2)s2+

(20-15λ2-5μ2)s3+(5λ2+5μ2)s4

由3.1小节中的结论可知,以Vi,0(s;λi,μi)为母线绕x轴旋转一周所得旋转曲面方程为

(19)

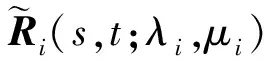
(20)

式中:xi,0(s)、yi,0(s)取式(18)中的值。

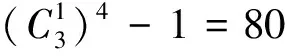
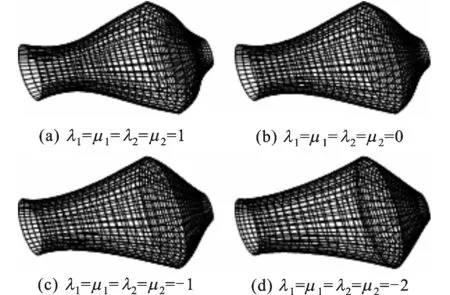
图1 同时改变参数λi、μi时的旋转曲面

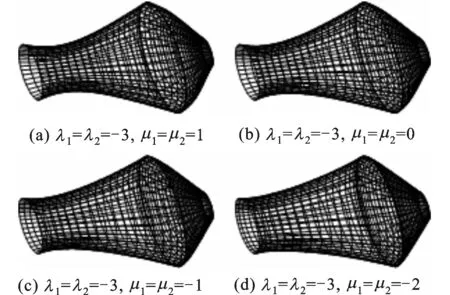
图2 固定参数λi、改变参数μi时的旋转曲面

图1～图4中的旋转曲面沿其母线方向只能达到G0光滑连续。若要使旋转曲面达到G1光滑连续,可按式(3)中的G1光滑拼接条件进一步修改式(17)中母线Vi,0(s;λi)(i=1,2)的控制顶点坐标。

图3 固定参数μi、改变参数λi时的旋转曲面

图4 参数λi=μi时的旋转曲面

实例2:试调整实例1中旋转曲面母线的控制顶点坐标,使得生成的旋转曲面沿其母线方向达到G1光滑连续。

解:为了使旋转曲面沿其母线方向达到G1光滑连续,根据定理1中的结论,首先需要将实例1中母线Vi,0(s;λi,μi)(i=1,2)的控制顶点调整为

(21)

图5给出了实例2中当形状参数取不同值时的沿母线方向达到G1连续的旋转曲面。从图5中可以看出,由于旋转曲面具有4个独立的形状参数,故其具有较好的形状可调性。

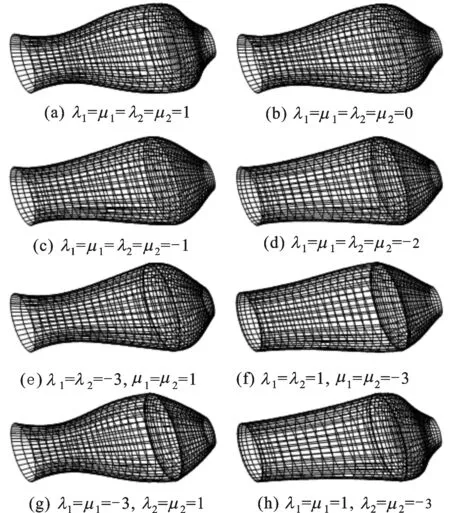
图5 沿母线方向G1连续的旋转曲面

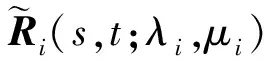
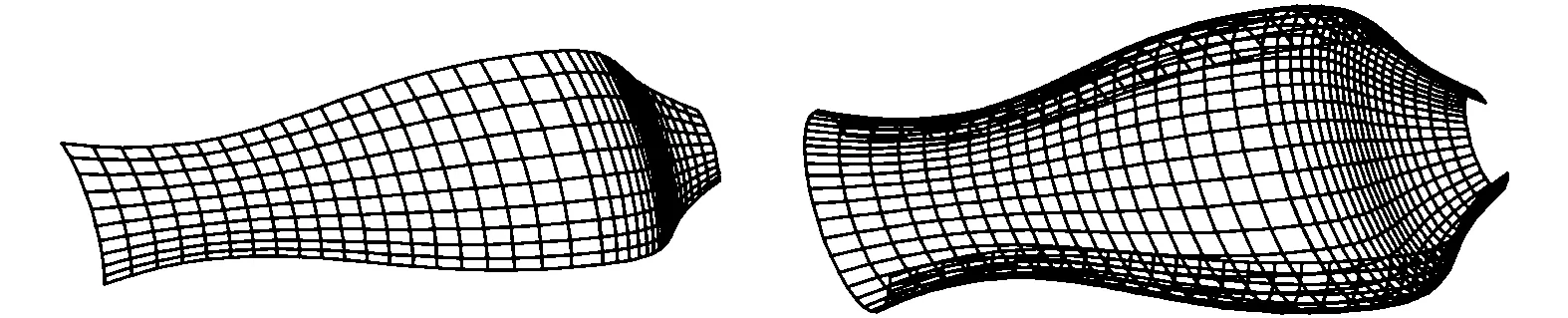
(a)θ=0.5π (b)θ=1.5π

5 结 论

基于超限向量值有理插值函数的重要思想,提出了一种设计四次拟Bézier旋转曲面的新方法。该方法具有如下优点:①通过引入形状参数可以修改旋转曲面的形状,极大地增加了旋转曲面造型的自由度;②克服了传统旋转曲面设计方法计算复杂的缺点,算法简单、高效;③给出了生成旋转曲面的显式函数表达式,不仅方便计算旋转曲面上点的坐标,而且有利提高旋转曲面的生成速度。理论分析与造型实例表明,本文方法在各种CAD/CAM造型系统中将有着十分广泛的应用价值。

[1] CHEN Q Y,WANG G Z.A class of Bézier-like curves [J].Computer Aided Geometric Design,2003,20(1): 29-39.

[2] ORUC H,PHILLIPS G H.q-Bernstein polynomials and Bézier curves [J].Journal of Computational and Applied Mathematics,2003,151(1): 1-12.

[3] HAN Xian,MA Yichen,HUANG Xili.The cubic trigonometric Bézier curve with two shape parameters [J].Applied Mathematic Letters,2009,22(3): 226-231.

[4] 檀结庆,王燕,李志明.三次H-Bézier曲线的分割、拼接及其应用 [J].计算机辅助设计与图形学学报,2009,21(5): 584-588.

TAN Jieqing,WANG Yan,LI Zhiming.Subdivision algorithm,connection and applications of cubic H-Bézier curves [J].Journal of Computer Aided Design & Computer Graphics,2009,21(5): 584-588.

[5] HAN Xian,MA Yichen,HUANG Xili.A novel generalization of Bézier curve and surface [J].Journal of Computational and Applied Mathematics,2008,217(1): 180-193.

[6] 胡钢,戴芳,秦新强,等.四次带参Bézier曲线曲面的光滑拼接 [J].上海交通大学学报,2010,44(11): 1481-1485,1490.

HU Gang,DAI Fang,QIN Xinqiang,et al.On continuity conditions for quartic Bézier curves and surfaces with shape parameters [J].Journal of Shanghai Jiaotong University,2010,44(11): 1481-1485,1490.

[7] 吴荣军,彭国华,罗卫民,等.四次带参Bézier曲线的形状分析 [J].计算机辅助设计与图形学学报,2009,21(6): 725-729.

WU Rongjun,PENG Guohua,LUO Weimin,et al.Shape analysis of quartic Bézier curve with shape parameter [J].Journal of Computer Aided Design & Computer Graphics,2009,21(6): 725-729.

[8] 胡钢,段献葆,秦新强,等.4次λ-Bézier曲线的近似合并算法 [J].华中科技大学学报,2011,37(9): 45-49.

HU Gang,DUAN Xianbao,QIN Xiqiang,et al.Approximate merging of a pair of quarticλ-Bézier curves with shape parameters [J].Journal of Huazhong University of Science and Technology,2011,37(9): 45-49.

[9] 胡钢,秦新强,韩西安,等.拟三次Bézier曲线曲面的拼接技术 [J].西安交通大学学报,2010,44(11): 46-50,60.

HU Gang,QIN Xinqiang,HAN Xi’an,et al.Continuity conditions for cubic quasi-Bézier curves and surfaces [J].Journal of Xi’an Jiaotong University,2010,44(11): 46-50,60.

[10]韩西安,马逸尘,黄希利.拟三次Bézier曲线的形状调整 [J].西安交通大学学报,2007,41(8): 903-906.

HAN Xi’an,MA Yichen,HUANG Xili.Shape modification of cubic quasi-Bézier curve [J].Journal of Xi’an Jiaotong University,2007,41(8): 903-906.

[11]FARIN G.Curves and surfaces for CAGD: a practical guide fifth edition [M].San Diego,USA: Academic Press,2002: 229-303.

[12]BOURGUIGNON D,CANI M P,DRETTAKIS G.Drawing for illustration and annotation in 3D [J].Computer Graphics Forum,2001,20(3): 114-122.

12].http:∥citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.104.8535&rep=rep1&type=pdf.

[14]韩丽,RAFFAELE D A.Cubic B样条旋转曲面的自由绘制技术 [J].小型微型计算机系统,2009,30(7): 1141-1144.

HAN Li,RAFFAELE D A.Rotation surface modeling technique by cubic B-spline free drawing [J].Journal of Chinese Computer Systems,2009,30(7): 1141-1144.

[15]檀结庆.连分式理论及其应用 [M].北京: 科学出版社,2007: 337-392.

[16]朱晓临.一种快速构造圆弧的新方法 [J].合肥工业大学学报,2002,25(2): 269-272

ZHU Xiaolin.A new method for constructing circular arc [J].Journal of Hefei University of Technology,2002,25(2): 269-272.

(编辑 杜秀杰)

NewMethodforConstructingQuarticQuasi-BézierRotationSurfaceswithMultipleShapeParameters

HU Gang1,SONG Weijie2

(1.School of Science,Xi’an University of Technology,Xi’an 710054,China;2.School of Science,Northwestern Polytechnical University,Xi’an 710072,China)

To deal with the problems in adjusting and controlling shapes of rotation surfaces,a new efficient method for quick constructing rotary surfaces with local shape parameters is proposed.Following the essence of transfinite vectored rational interpolating function,the quartic quasi-Bézier rotary surfaces with multiple shape parameters are constructed and the explicit function for quartic quasi-Bézier rotary surfaces is presented.The so constructed surfaces inherit the outstanding properties of the Bézier rotary surfaces with good performance in adjusting local shapes by changing the shape parameters.Some properties of the quartic quasi-Bézier rotary surfaces and applications to surface design are discussed.

quartic quasi-Bézier curve; shape parameter; rotary surface; transfinite vectored rational interpolating function

2013-09-28。

胡钢(1979—),男,副教授。

国家自然科学基金资助项目(51305344);国家自然科学基金重大研究计划培育项目(91120014);陕西省教育厅基金资助项目(2013J K1029)。

时间:2014-03-06

10.7652/xjtuxb201406013

TP391.4

:A

:0253-987X(2014)06-0074-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140306.1027.002.html