数控机床基础大件精度保持性研究

胡敏,余常武,张俊,赵万华,寸花英,袁胜万

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.沈机集团昆明机床股份有限公司,650203,昆明)

数控机床基础大件精度保持性研究

胡敏1,余常武1,张俊1,赵万华1,寸花英2,袁胜万2

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.沈机集团昆明机床股份有限公司,650203,昆明)

针对国产机床生产厂家振动时效工艺不规范导致数控机床基础大件精度保持性较差这个问题,提出了一种振动时效工艺参数选择方法。该方法通过模态分析和谐响应分析的方法对振动时效的工艺参数进行合理选择。在此基础上,对两个相同床身分别在原振动时效工艺和新振动时效工艺下进行振动时效的效果评价试验,结果表明,新工艺下的振动时效平均应力消除率为65.1%,原工艺下为38.5%,新振动时效工艺下床身的应力消除率是原振动时效工艺下的1.69倍。由此验证了提出的新振动时效工艺的正确性和有效性,表明该方法能够显著提升数控机床基础大件的精度保持性。

机床基础大件;精度保持性;几何误差模型;振动时效;盲孔法;应力消除率

国产数控机床的精度会随着时间慢慢变差,而数控机床基础大件的精度保持性是影响其精度变差的主要原因之一。数控机床的基础大件在铸造过程中,由于结构复杂以及铸造技术等因素的影响,导致铸件冷却不均而在铸件内部产生残余应力[1]。目前,我国机床生产厂家通过人工时效的方法减小和均化大型铸件的残余应力,但是由于人工时效工艺不规范以及未对时效后的铸件应力消除效果进行评价,目前我国数控机床上大型铸件的精度保持性普遍比较差。

本文通过对某卧式加工中心的床身部分进行应变监测,得到床身随时间的变形关系。同时,通过对各零部件的几何要素进行表征,并通过零部件上用于表征几何要素的3个最高点确定基准平面的方法,确定两零部件之间的坐标转换关系,从而建立起床身变形和工作台面与地基理想平面的平行度误差的传递关系。在此建立的几何误差模型中提到的两零部件之间的坐标转换关系与基于多体运动学理论的几何误差模型所使用的齐次坐标变换[2-5]有一定的区别。由于工作台面与地基理想平面的平行度误差是该卧式加工中心的主要几何误差,同时床身变形是引起该平行度误差变化的主要原因,因此以该平行度误差作为本文的研究对象。通过理论计算值与实测值对比表明,该卧式加工中心床身在3个月内的变形是导致其工作台面与地基理想平面的平行度误差变化的主要原因,而导致床身变形的主要因素是人工时效不充分,残余应力消除效果不佳。

目前,消除铸造残余应力的方法主要有自然时效、热时效以及振动时效。文献[6]表明热时效后工件疲劳寿命下降了43%,而振动时效后工件疲劳寿命则增加了17%～30%。由于热时效能耗大、成本高、大件处理困难,以及自然时效耗时长、效率低,目前国内机床生产企业更多的选择振动时效工艺来进行铸造内应力的消除。国内机床生产厂家对振动时效工艺参数一般依据经验进行选择,但是经过企业振动时效工艺后的基础大件,在机床装配过程中精度会发生明显的、不可逆的变化。这说明企业目前采用的振动时效工艺的效果不佳,铸造内应力消除不够充分,导致零件在内应力释放作用下发生变形。此外,虽然目前有很多振动时效效果测量和评价方法[7-8],但是企业并未对工艺效果进行评价,导致企业未能认识到自身工艺的问题。Li等采用有限元仿真方法得到各阶阵型,从而确定振动时效的工艺参数,但只是简单地采用一阶阵型作为确定振动时效工艺参数的依据,未对阵型作合理的选择,同时最后振动时效的效果也仅作了定性的分析,未作定量的应力消除评价[9]。

本文提出了一种振动时效工艺参数的选择方法,可以实现振动时效工艺参数的合理选择,并通过试验验证了新工艺能够显著降低基础大件的残余应力,从而提高数控机床基础大件的精度保持性。

1 机床基础大件精度衰退情况

1.1 几何误差模型

某卧式加工中心Z轴的结构如图1所示,由于轴向径向轴承和导轨滑块属于标准件,其精度等级高于其他结构件,因此在分析尺寸链时不考虑,另外由于机床安装的地基随时间几乎不发生变化,因此不影响几何误差分析。由此,可以得到工作台面与地基平面之间平行度的尺寸链,如图2所示,其主要组成环包括工作台、工作台底座以及床身。

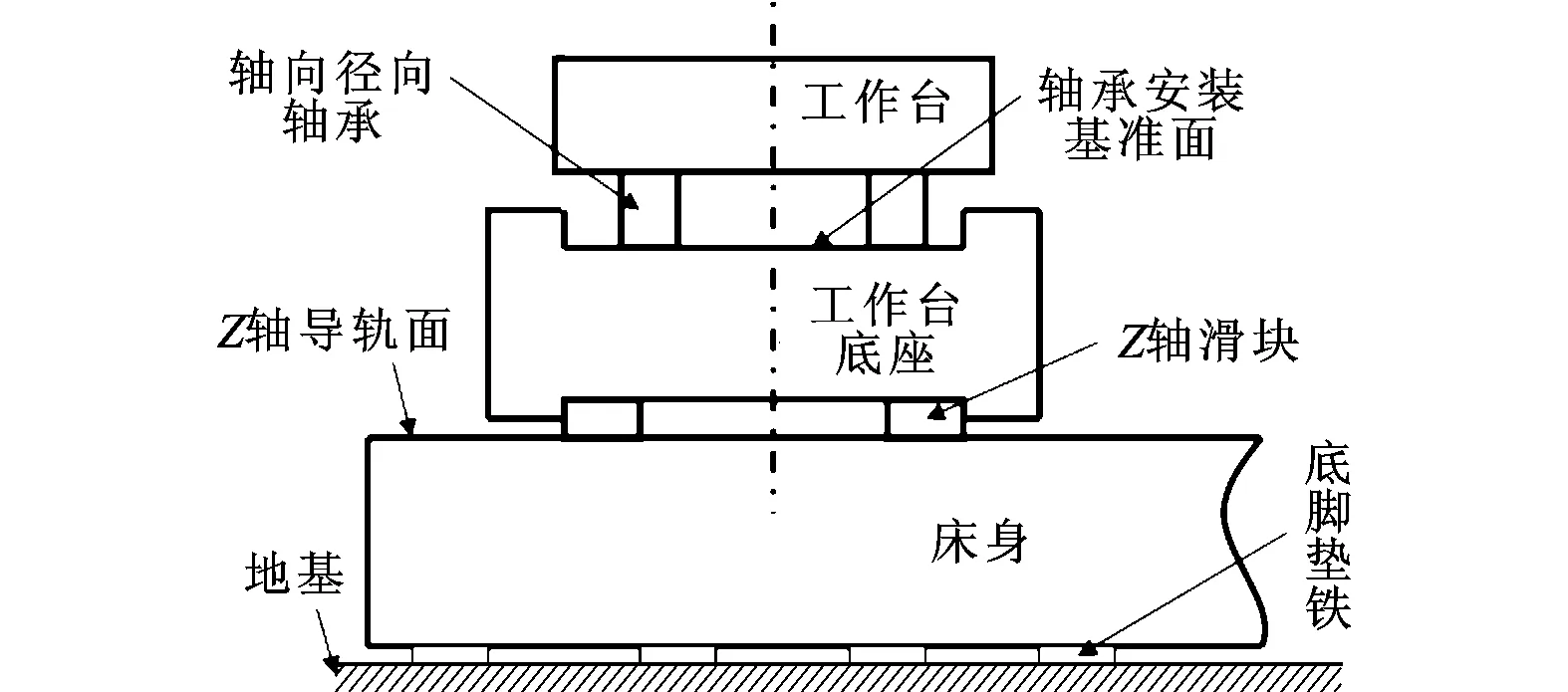
图1 某卧式加工中心的Z轴结构示意图

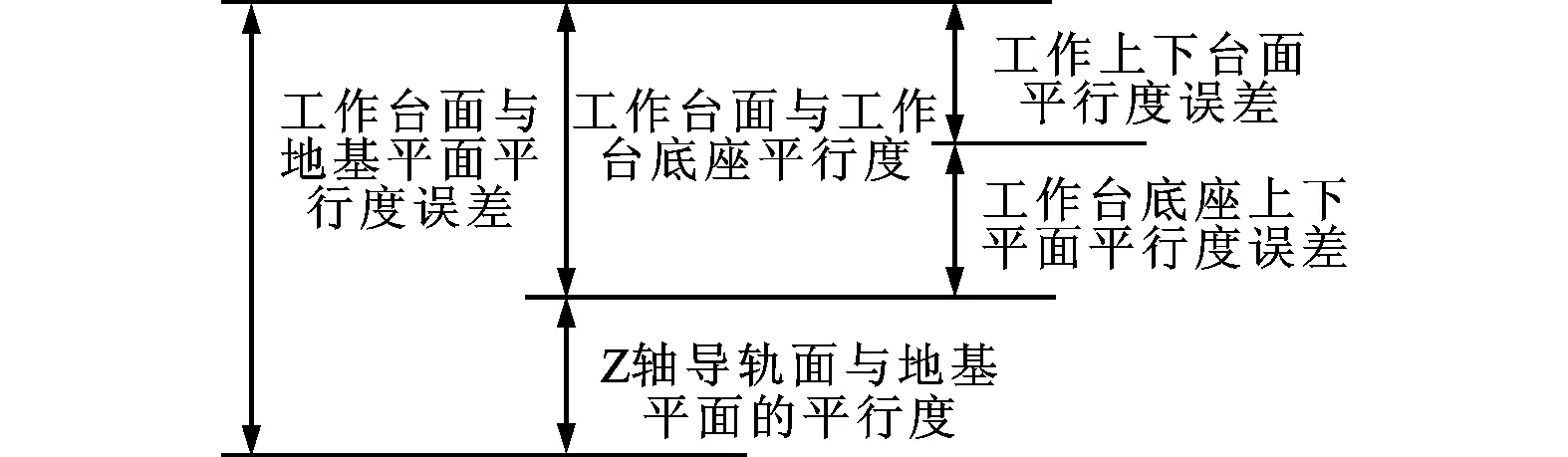
图2 工作台面与地基理想平面的平行度尺寸链示意图

1.1.1 误差表征 各组成环上误差分布对最终的几何误差会产生影响,因此首先需表征出各组成环中的误差信息。在各组成环中分别建立坐标系,其上误差信息与坐标位置有关,因此采用坐标点的形式表示误差

δ=(X,Z,Y+δY,1)T

(1)

式中:X、Z为坐标点的位置;δ为相应坐标位置处的误差;Y为组成环尺寸;δY为组成环尺寸的变动量。

由此可以得到各组成环上误差表示方法,床身、工作台底座以及工作台坐标系见图3,各部件的误差信息为

δ1=(X1,Z1,Y1+δY1,1)T

(2)

δ2=(X2,Z2,Y2+δY2,1)T

(3)

δ3=(X3,Z3,Y3+δY3,1)T

(4)

式中:Y1为床身导轨面到地基的高度;Y2为工作台底座上下面间的距离;Y3为工作台上下面的距离。

(a)床身 (b)工作台底座 (c)工作台

1.1.2 坐标转换关系 各组成环之间的装配关系可以表示为其坐标系之间的转换关系,如图4所示,而坐标系之间的相对位置关系又是由其装配工艺决定的,具体取决于两构件相互结合的基准面,这里采用构件结合面上的最高3点确定的平面作为基准平面。

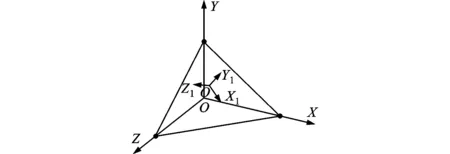
图4 坐标系之间的转换关系

设结合基准面上的最高3点坐标分别为(X1max,Z1max,δi)、(X2max,Z2max,δj)和(X3max,Z3max,δk),则由此3点得到平面上两向量分别为

a=(aX,aZ,aY)=

(X1max-X2max,Z1max-Z2max,δi-δj)

(5)

b=(bX,bZ,bY)=

(X1max-X3max,Z1max-Z3max,δi-δk)

(6)

由此可以得到基准平面法向量为

c=a×b=(cX,cZ,cY)

(7)

基准平面的方程如下

(x-X1max)cX+(z-Z1max)cZ+(y-δi)cY=0

(8)

根据组成环的装配关系,O1X1Y1平面与三点确定的基准平面相重合,而O1Z1或O1X1与理想坐标系OXYZ的位置关系取决于装配过程中的定位面,装配过程中工作台面与地基理想平面的平行度是以YOZ平面作为基准面,因此O1Z1一定在YOZ平面内,O1Z1与Z轴之间的夹角计算式为

γ=-arctan(cZ/cY)

(9)

γ在坐标系OXYZ中的位置为(0,sinγ,cosγ),O1X1决定于O1Y1和O1Z1,在OXYZ坐标系中的位置为

X01=(X01X,X01Z,X01Y)=

(cX,cZ,cY)×(0,sinγ,cosγ)

(10)

1.1.3 某卧式加工中心的几何误差模型 采用坐标点形式表示出各组成环上的误差信息后,结合坐标之间的位置关系可以得到相应的几何误差模型,由式(5)～式(10),可以得到坐标变换矩阵为

(11)

式中:(α1,α2,α3)、(β1,β2,β3)和(γ1,γ2,γ3)分别表示O1X1、O1Y1、O1Z1坐标轴与OXYZ坐标系3个坐标轴的夹角;ΔY表示两坐标系原点之间的距离

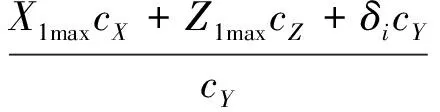
(12)

由此得到工作台面与地基理想平面的平行度尺寸链中各个组成环之间的转换矩阵A01、A12和A23,那么工作台面上各点在地基坐标系中的坐标为

δ=A01A12A23δ3

(13)

由此建立了某卧式加工中心工作台面与地基理想平面的平行度的几何误差模型,结合工作台面与地基平面平行度的测量方法,可计算出相应的误差。

1.2 基础大件精度衰退监测及数据分析

在建立的几何误差模型的基础上,可以利用长期自然状态监测到的某卧式加工中心床身应力应变信息,分析床身变形对工作台面和Z轴线运动间平行度的影响。

对某卧式加工中心床身部分在3个月内的应变跟踪监测,采用应变片监测床身随时间的应变变化情况,从而间接反映出床身各处的变形情况如图5所示。图6所示为3个月内应变(标幺值,全文同)的变化情况,根据弯曲变形特点,应变值为正表示床身向上凸、为负表示床身向下凹,可以间接反映出床身各点的变形信息。这一变化对工作台面与地基平面间平行度产生影响,但二者没有直接对应关系,需要根据建立的几何误差模型,由状态监测数据得出床身变形对平行度产生的影响。

图5 床身在3个月内的应变监测示意图

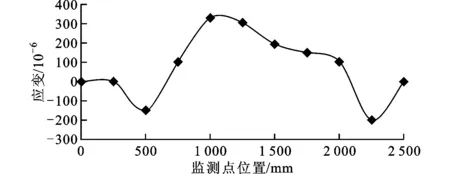
图6 床身状态监测点在3个月内的变化

图7为测量工作台面和Z轴线运动间平行度的示意图,在工作台中间位置沿Z轴线放置平尺,在主轴箱上固定指示器,沿Z轴线移动工作台检验各处读数。由于测量位置在工作台中间,可以将前述得到的几何误差模型进一步简化到YOZ平面内进行分析,而且是在工作台台面上搁置平尺进行测量,因此最终得到的数据还与平尺的测点位置相关,其几何误差模型示意图如图8所示。由于平尺的精度等级高于被测量,可以不考虑它的误差因素,另外,这里主要分析床身变形对平行度的影响,因此将工作台和工作台底座组合考虑。

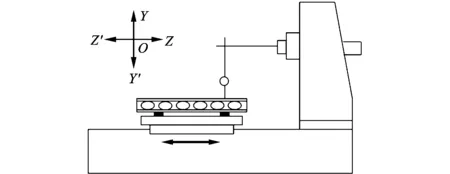
图7 工作台面和地基平面间平行度测量示意图

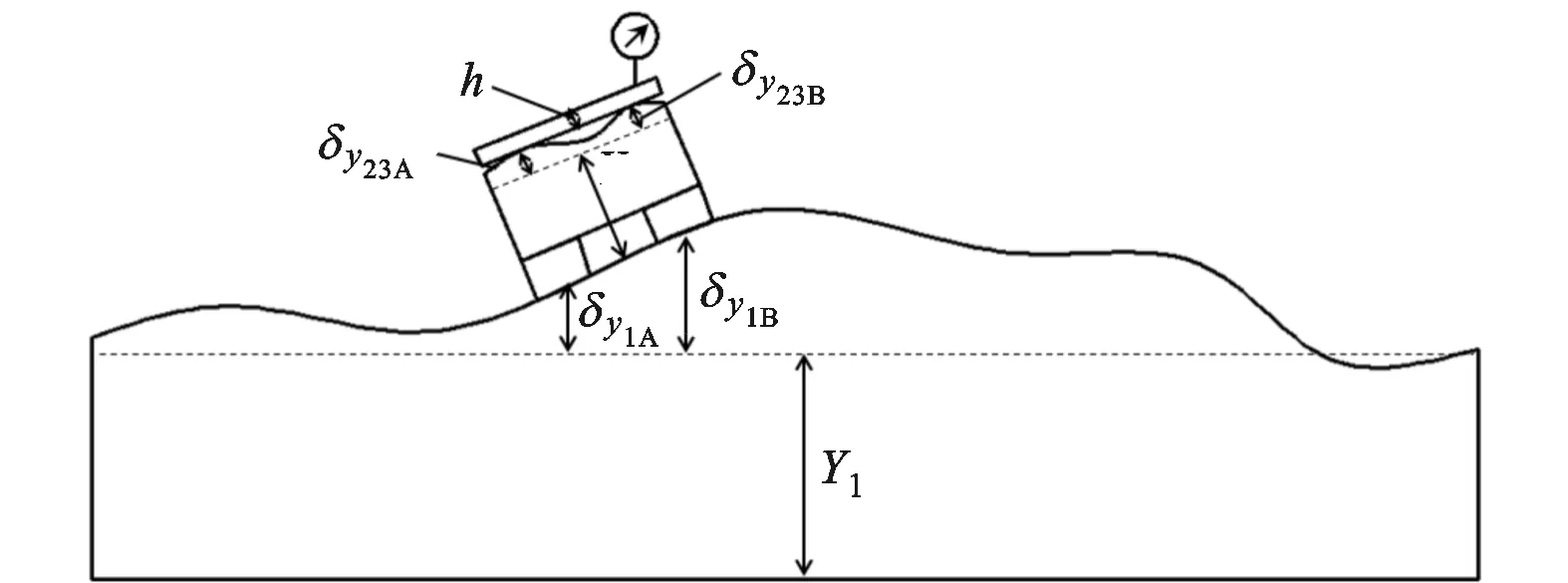
h表示平尺的高度;Y1和Y23分别表示床身和工作台部分相关的尺寸;δy1A和δy1B表示滑块所在位置导轨的误差;δy23A和δy23B分别表示工作台最高两点的误差

根据几何误差模型,在二维情况下可以得到平尺测量点在地基坐标系中的位置,忽略高阶小量,则结果为

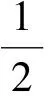
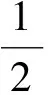
(14)

式中:k是与平尺上测点位置相关量。由于与床身和工作台部分相关的尺寸以及平尺尺寸不随时间变化,一段时间后,测点位置的变化可以表示为

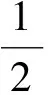
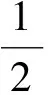
(15)

式中:Δδy1A和Δδy1B为床身状态监测的数据点,代入监测数据可以得到床身变形对工作台面与地基平面间的平行度产生的影响,如图9a所示。在床边应变监测试验开始前和结束后,分别对工作台面与地基平面的平行度误差进行测试,得到的平行度变化情况见图9b。

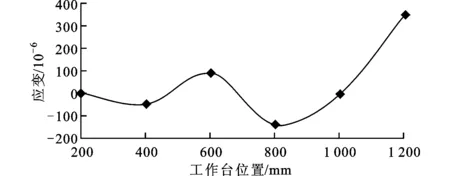
(a)床身变形产生的影响

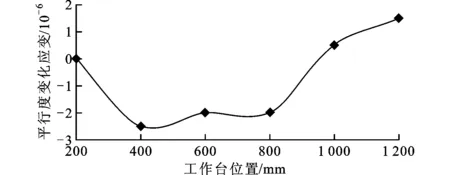
(b)3个月内的变化情况

从图9中可以看到,工作台面与地基平面的平行度误差变化趋势与床身应力变化趋势相同,这初步表明床身变形是影响平行度变化的主要因素。

2 振动时效工艺参数选择方法

在实际制造过程中,企业采用的振动时效工艺的效果不佳,铸造内应力消除不够充分,导致基础大件在内应力释放作用下发生变形,上述的应变监测试验很好地证明了这一点。虽然目前有很多振动时效效果测量和评价方法,但是企业并未对振动时效工艺的效果进行评价,导致企业未能认识到自身工艺存在的问题。目前对机床基础大件进行振动时效分析时,其主要工艺参数为:激振频率、激振点和拾振点、支撑点、激振力以及激振时间。

2.1 振动时效机理

从振动时效消除铸件残余应力的机理角度分析,振动时效消除铸件残余应力应满足的条件是动应力(激振力)和残余应力之和大于材料的屈服极限。若以σd表示动应力(激振力)、σr表示残余应力、σs表示屈服极限,则振动时效应满足

σd+σr≥σs

(16)

当式(16)成立时,在铸件内残余应力的某些高峰值点处将产生局部屈服,引起局部微小塑性变形,使铸件内部残余应力高峰值降低并使铸件内部残余应力重新分布并均化,提高了铸件特别是机床基础大件精度的保持性。除了满足式(16)以外,动应力σd应小于铸件的疲劳极限,即满足

σd≤σ-1

(17)

通过激振仪器提供的动应力应满足

σs-σr≤σd≤σ-1

(18)

由于机床基础大件内的残余应力大小不等,因此为了尽可能地降低并均化铸件内的应力,式(18)中的σr取平均值,而铸造后的残余应力可通过仿真分析得到,并通过试验验证了其正确性。

2.2铸造残余应力σr的获取

2.2.1 铸造残余应力的仿真分析 如图10所示的床身大件,床身材料为HT250,材料参数如表1所示。灰铸铁材料弹塑性转变温度范围为350～450℃,在初步仿真分析中,近似认为在弹性变形阶段,灰铸铁材料参数为常值。仿真软件采用Solidworks中的Simulation仿真模块。

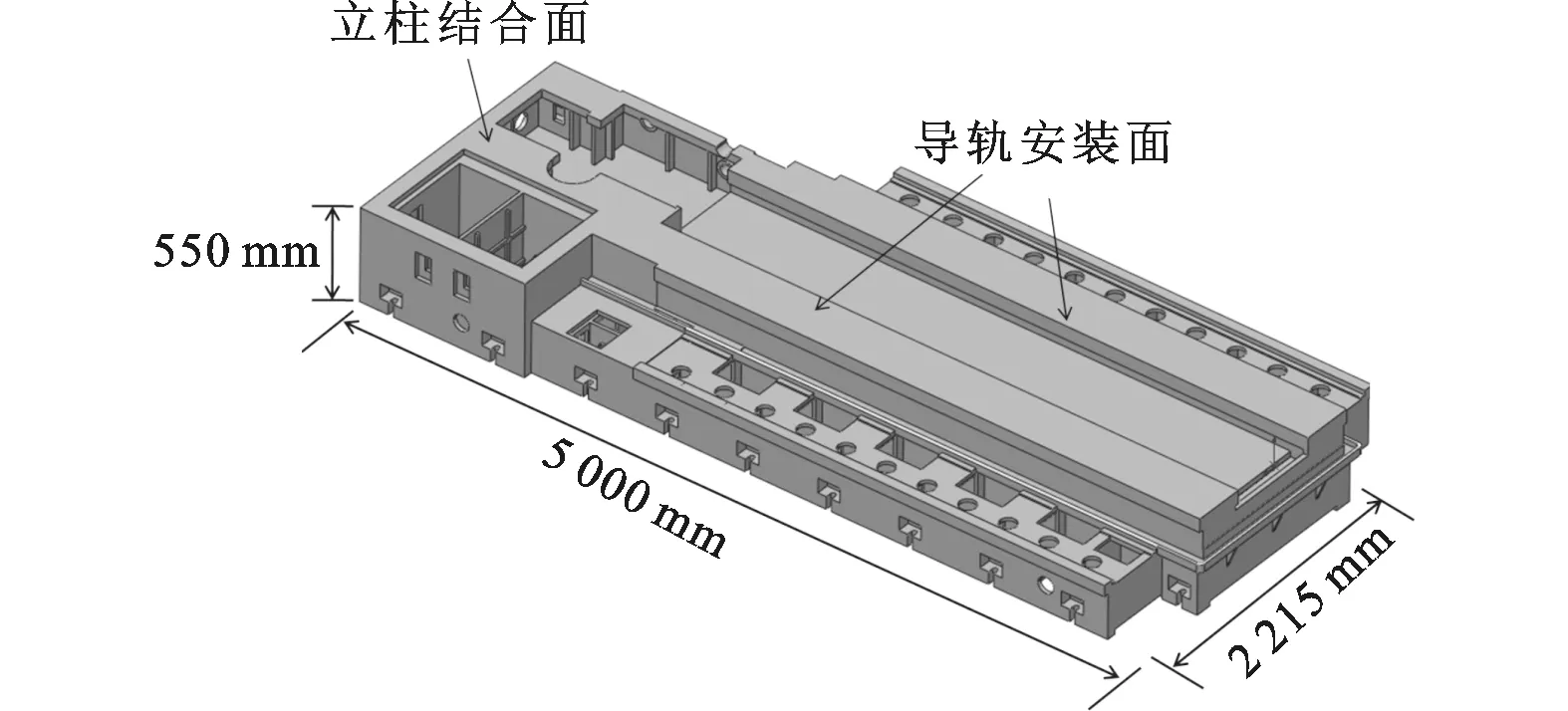
图10 床身结构示意图

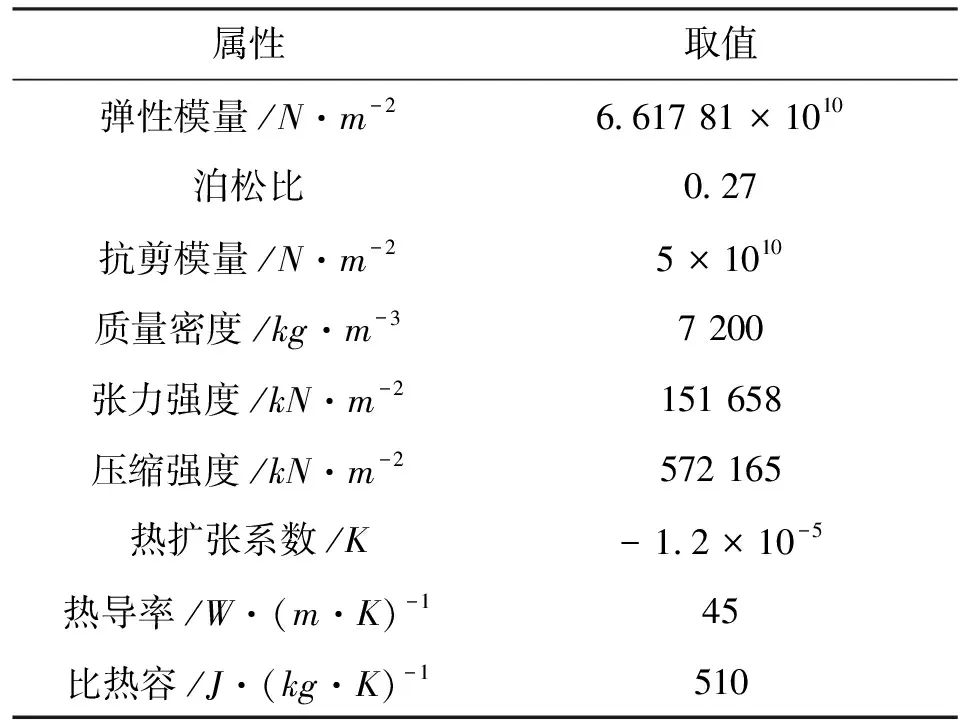
表1 HT250材料参数

在热载荷里设置初始浇注温度为1 350℃,由于要使铸件的收缩方向一致,对铸件两个对称的中性面进行固定约束,选择弹塑性温度区间在350～450℃之间。床身在铸造冷却过程中,各部分都处于弹性变形阶段时的温度场如图11所示,导轨面处的温度为400～450℃,符合灰铸铁的弹塑性转变温度。

图11 床身各部分均处于弹性变形阶段的温度场

将图11中的温度场作为载荷施加到床身上,得到床身在铸造过程中由热应力的影响形成的铸造残余应力见图12,用各处的第一主应力σ1表示。

此外,对床身残余应力进行检测,得到导轨面一条线上的各节点的第一主应力如图13所示,可以看到第一主应力主要在110MPa左右波动。

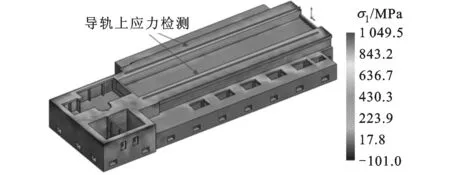
图12 床身残余应力分布情况

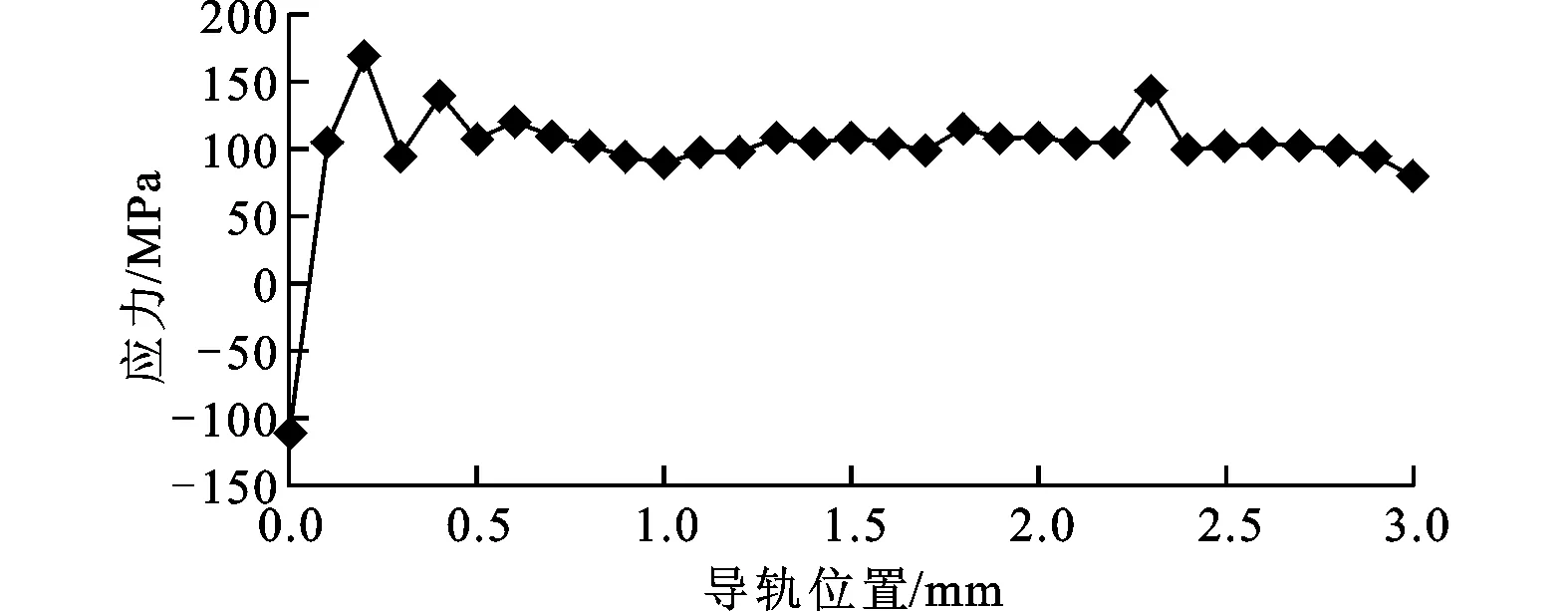
图13 导轨面检测线上的应力情况

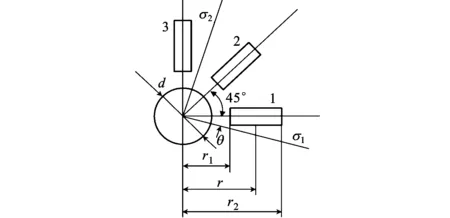
图14 盲孔法测应力原理

2.2.2 试验验证 图14所示为盲孔法测内应力的原理,在铸件上钻一不通孔,使被测点处的应力得到释放,并由事先贴在孔周位的应变计测得释放的应变量,根据弹性力学原理,计算测试点处的主应力

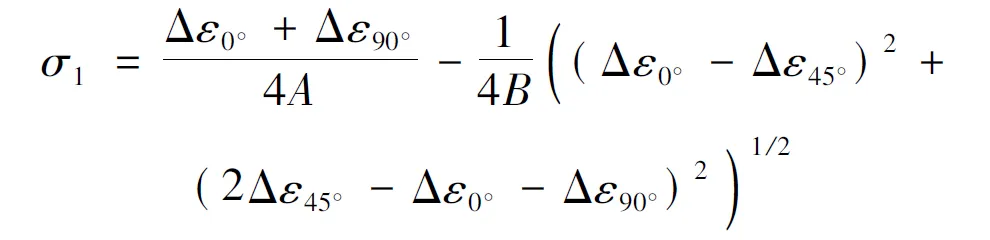
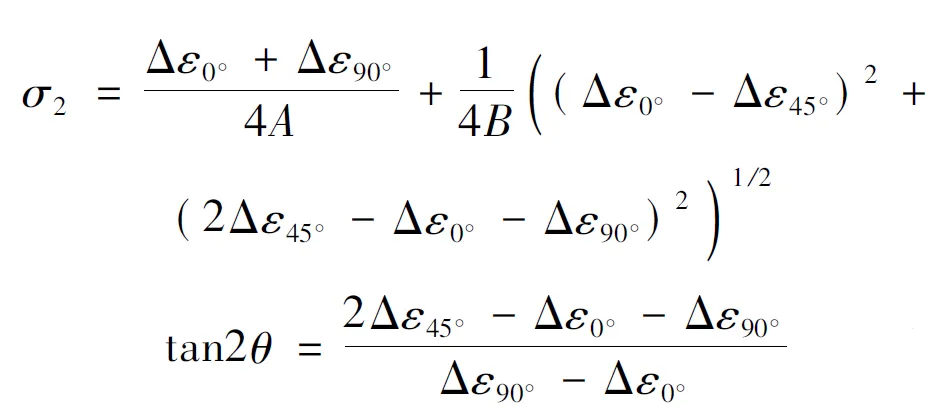
(19)

式中:Δε0°、Δε45°和Δε90°为3个方向应变变化值;θ为两主应力之间的夹角。

根据美国材料学会制定的ASTM标准[10]E 837—81,利用盲孔测应力方法,分别对床身导轨面上的内应力进行测试,6个测点的位置如图15所示,测试现场如图16所示。

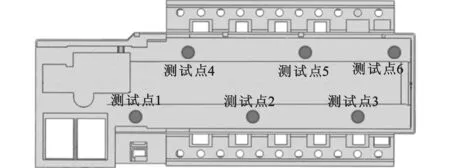
图15 盲孔法测内应力的位置布局

图16 盲孔法测内应力的测试现场

由仿真得到的导轨面上应力为110MPa以及文献[11]的结论,对于此床身,可以确定试验中选用的应力释放系数A、B分别为-0.021 05和-0.2702,通过式(19)计算的床身导轨面应力见表2,其中Δε1、Δε2、Δε3分别为测量点0°、45°、90°三个方向的应变。

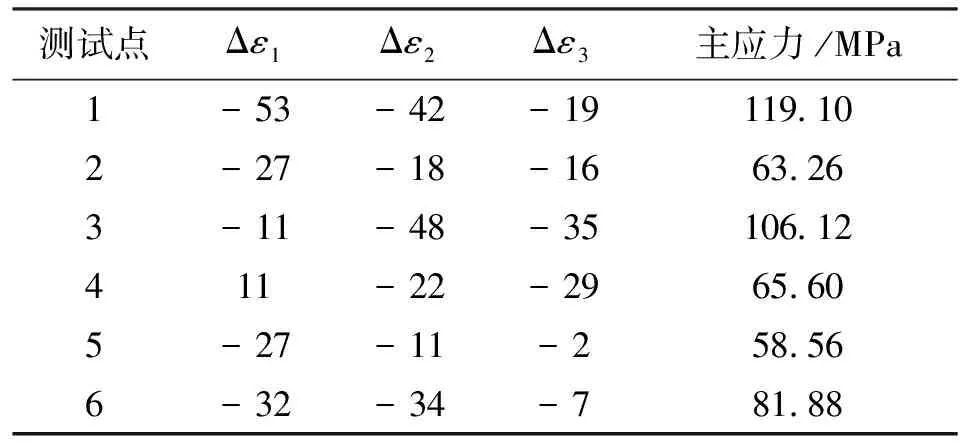
表2 床身导轨6个测点的应力情况

对实际铸造工艺下的床身导轨面的残余应力进行测试可知,导轨面的平均残余应力为82.24MPa,而仿真值为110MPa,验证了有限元仿真理论具有一定的可信性,在振动时效工艺参数的选择方法中,床身的残余应力σr记为110MPa。

2.3 振动时效工艺参数选择

振动时效机理是:通过外部施加应力与内部残余应力叠加,超过材料屈服极限,从而使材料局部发生塑性变形,这种塑性变形首先发生在残余应力最大处,使该处的约束变形得以释放,从而达到工件残余应力降低、尺寸稳定的目的[12]。因此,振动时效参数主要为:激振点及拾振点的选择、支撑点布局、激振频率、激振力和激振时间。

目前,企业在进行振动时效工艺参数选取时主要依据经验进行,参数的选取如表3所示。选择表3所示的参数能够实现对铸件的共振,也能起到一定的内应力消除作用,但其效果不好,在实际使用过程中多次发生过由于床身变形导致加工精度下降,被迫采用刮研导轨面来保证最后的加工精度。

表3 企业现场振动时效参数选择

本文提出依据铸件模态仿真分析以及谐响应分析的振动时效参数选择方法,以图10所示的床身为例,进行振动时效工艺参数选择方法说明,具体如下。

(a)一阶阵型 (b)二阶阵型 (c)三阶阵型

(1)模态仿真分析。对图10所示床身进行自由模态分析,得到其前三阶的振型及振动频率,如图17所示。床身的第一阶阵型为两个对称角的翘曲,第二阶阵型为垂直面内的波浪振动,第三阶阵型为床身4个角及较薄边缘的翘曲振动。床身的前三阶固有频率分别为63.6、82.6和122.7Hz。床身的第二阶振型是整体波浪振动,且振动方向适合激振,因此选择第二阶振型为时效参数选择的基础,由此得到支撑位置、激振点及拾振点的位置如图18所示。

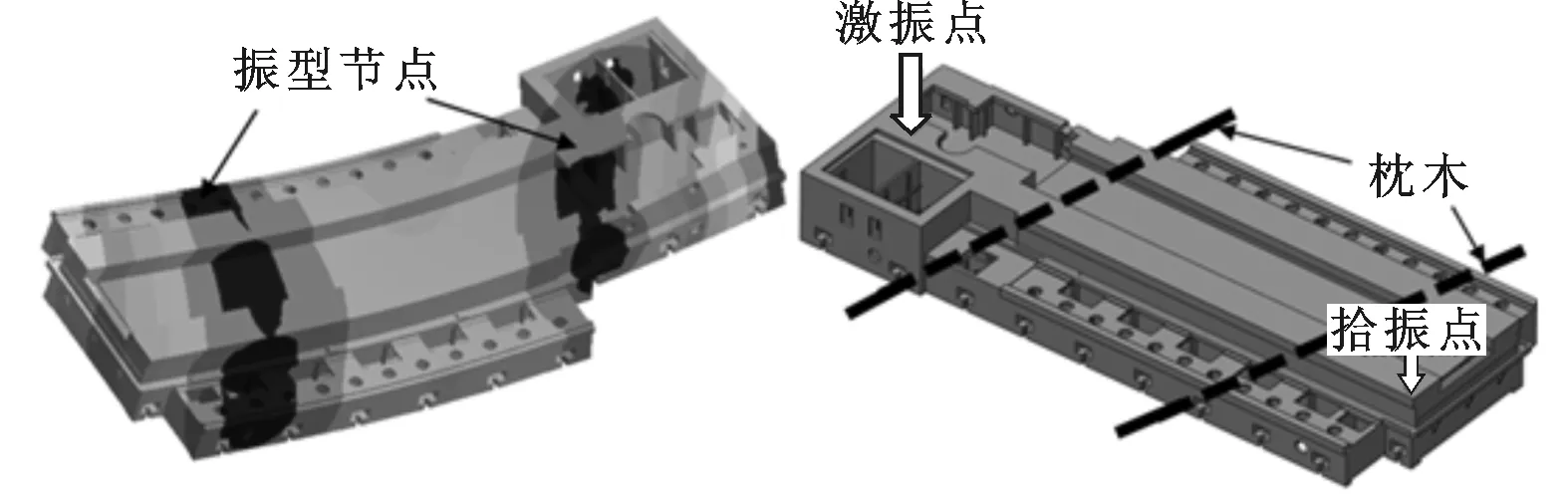
图18 最佳的支撑点、激振点和拾振点布局示意

随着振动的进行,铸件的固有频率会降低,且在固有频率下的振动在激振时不稳定,故选用亚共振区的品级进行激振,表达式为

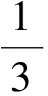
(20)

式中:ω0、ω1为固有频率,ω0-ω1=ζω0,ζ为材料阻尼比。由于床身的二阶固有频率为82.6 Hz,按式(20)计算得到激振频率为81.5 Hz。同时,铸件重6.7t,因此激振时间应为40min。

(2)谐响应分析。为了确定振动时效过程中应该施加多大的激振力,必须分析所施加的激振力与铸件内的动应力的关系,根据铸件需要的动应力决定激振力的大小。由于振动时效仪器施加的力为简谐力,因此对铸件进行谐响应分析,模拟振动时效过程,分析激振力和动应力的关系。

对床身激振点施加F=F0cos(wt)的简谐激振力,得到F0分别为30、40、50、60kN时的最大动应力与激振力的对应关系,如图19所示。由图可知,在激振力分别为60、50、40、30kN时,床身的最大动应力分别为150、125、98.5和73.9 MPa。由式(18)可知,动应力应满足如下条件:60MPa≤σd≤130MPa,其中σs=180MPa,σr=110MPa,σ-1=130MPa。结合图18,可知激振力应取50kN,以使激振效果最佳。

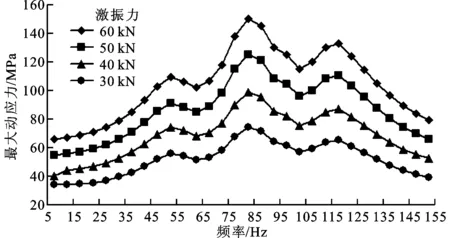
图19 不同激振力下的谐响应曲线

3 振动时效参数选择方法的验证试验

3.1 振动时效效果评价方法

通过模态仿真分析方法以及谐响应分析方法对某床身的振动时效工艺的参数进行定量的选择,其应力消除效果由试验进行定量的评价,试验的目的在于验证两种参数选择方法的振动时效效果。为了对振动效果进行评价,本文采用盲孔测应力法,对试验用床身导轨面的应力进行测试,试验流程如图20所示。选择刚铸造完毕但未进行振动时效的两个相同床身,分别记为床身A和床身B,其三维模型如图10所示,利用盲孔法分别对两个床身进行导轨面的应力测试,得到两床身振动时效前的应力。然后,对床身A和床身B分别利用本文提出的振动时效工艺参数和原振动时效工艺参数进行试验,再利用盲孔法进行时效后的应力测试。最后,对比两种工艺参数下时效前后的应力消除率,对两种方法的振动时效效果进行了对比验证,其中测点的布置如图15所示。

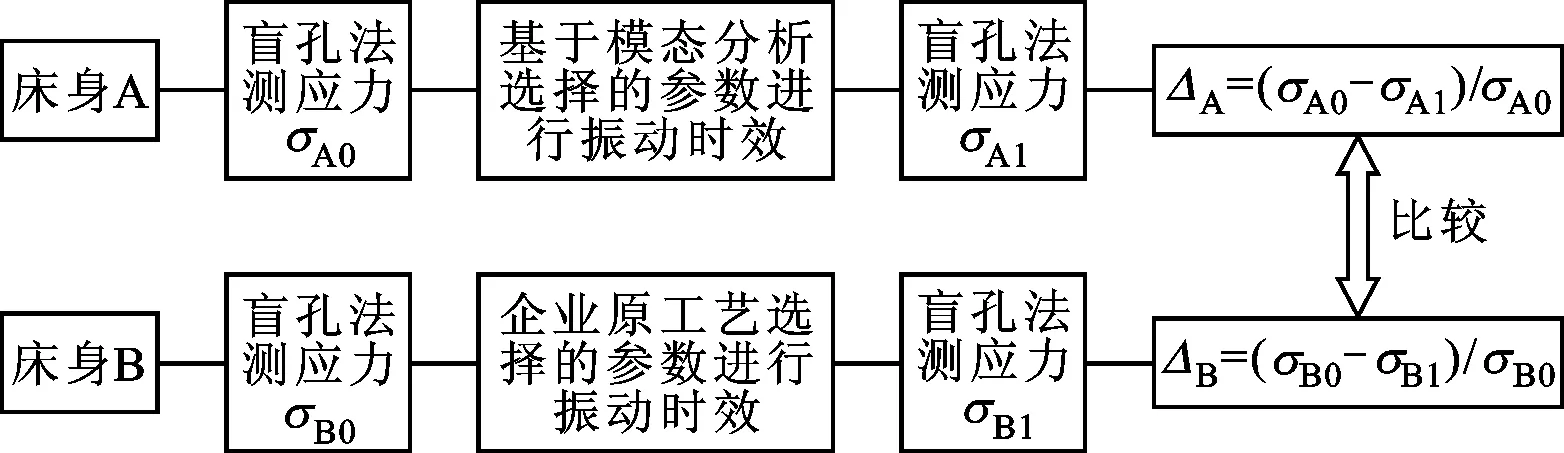
图20 验证试验流程图

3.2 振动时效工艺参数选择

(1)利用本文提出的工艺参数选择方法,对激振频率、激振点和拾振点、支撑点以及激振时间进行选择,各参数位置见图18,参数值见表4。本文选择对床身A的激振力为50kN,振动时效现场如图21所示,由于现场环境限制床身的支撑不能拍摄到。

图21 新工艺振动时效现场

(2)利用原工艺参数对床身B进行振动时效。企业选择的工艺参数中,支撑位置、激振点及拾振点位置如图22所示,激振频率和激振时间如表4所示,选择激振力为30kN,对床身B进行振动时效的现场如图23所示。

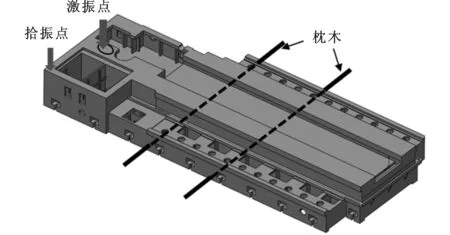
图22 振动时效支撑点、激振点和拾振点布局示意图

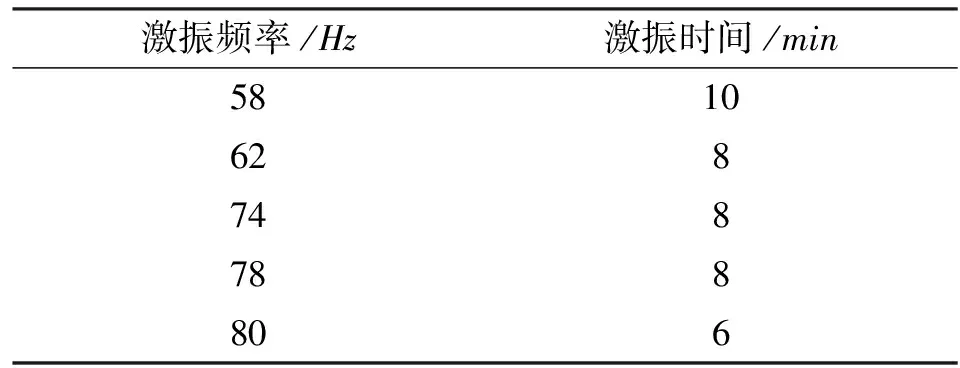
表4 企业现场对该床身振动时效参数的选择

在振动时效前后,分别对床身A和B再次进行盲孔法残余应力测试,钻孔位置与振动时效前位置相近,约相距5 cm。

图23 原工艺振动时效现场

3.3 试验数据及结果

通过静态应变测试仪测得床身A、B在振动时效前后导轨面各测试点处的应变变化情况,利用文献[10-11]方法计算得到两床身时效前后的应力值,从而计算出各测试点处的应力消除率,见表5和表6。

如表5所示,按照本文工艺参数选择方法,床身A的6个测试点处的主应力值均有所下降,平均的应力消除率为65.1%。如表6所示,按照原工艺时效参数处理的床身B,有5个测试点的主应力值下降,这5个点的平均应力消除率为38.5%,但测试点4处的主应力值有所增加。在本文工艺参数下,应力消除率明显优于原工艺,结果如表7所示。

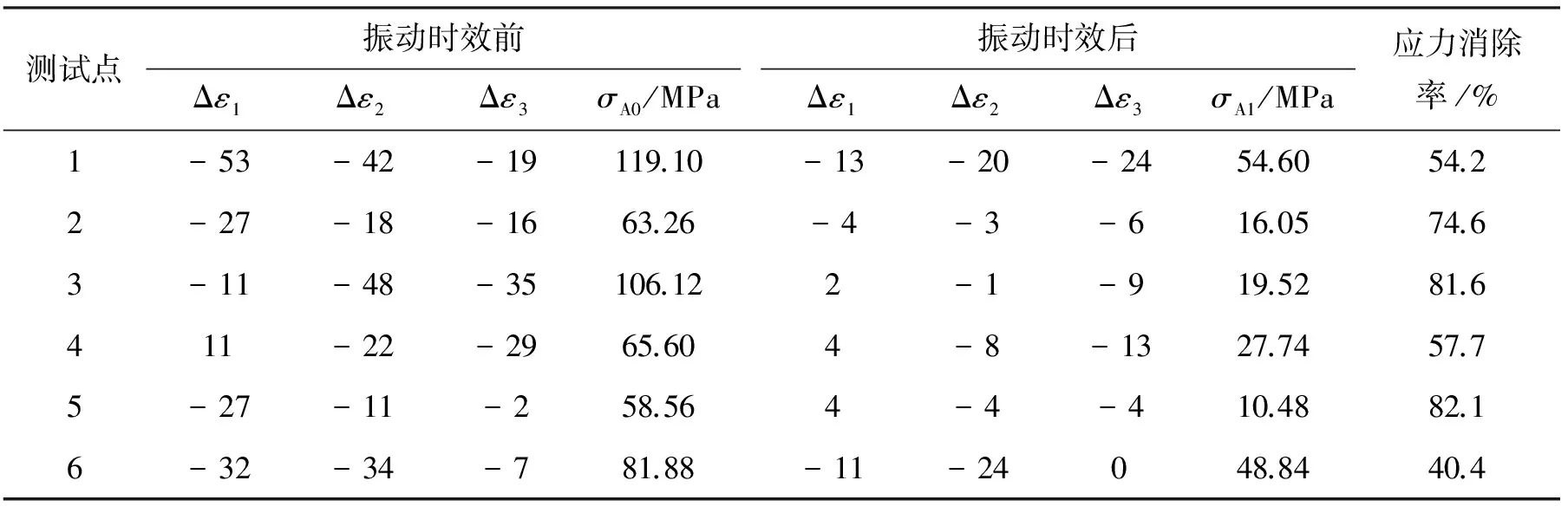
表5 本文工艺对床身A的应力消除率

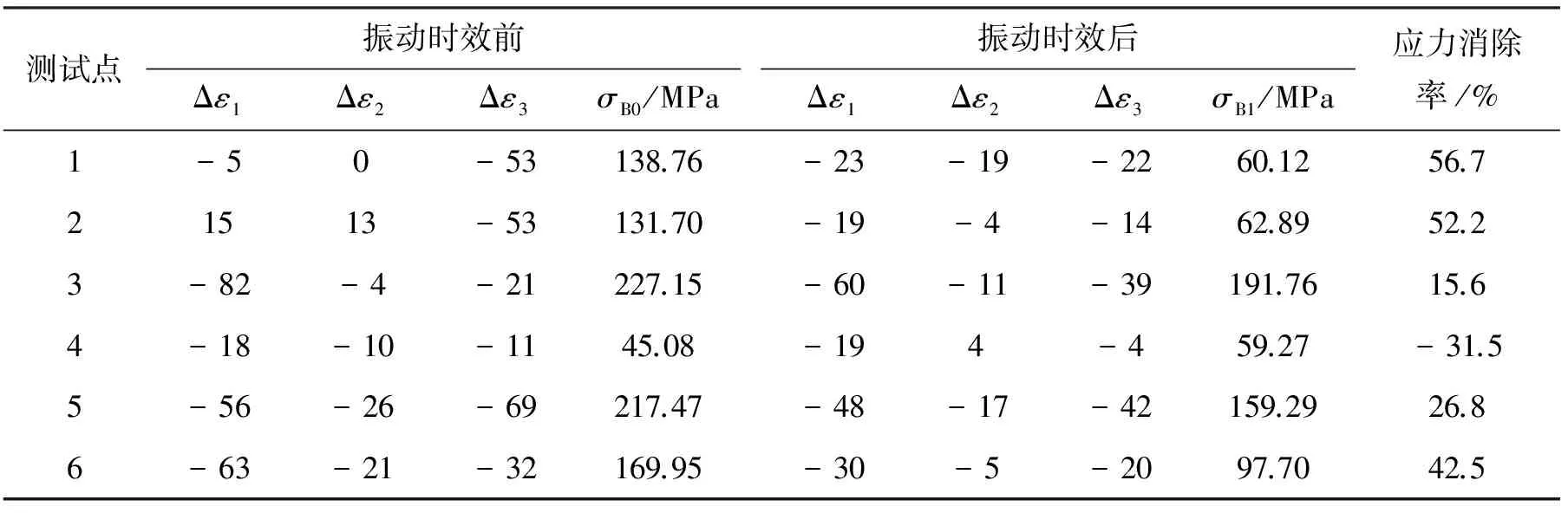
表6 原工艺对床身B的应力消除率

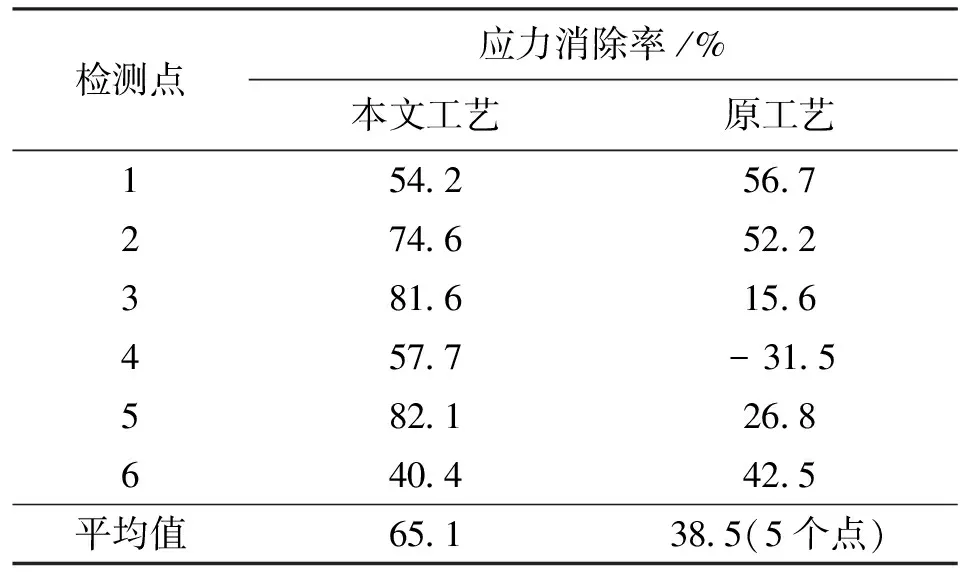
表7 本文工艺与原工艺下的应力消除率对比

通过上述验证可知,本文工艺的平均应力消除率是65.1%,原工艺为38.5%(测试点4应力增加),本文工艺的平均应力消除率为原工艺的1.69倍。试验结果证明了通过模态分析以及谐响应分析的方法对振动时效工艺参数进行优化的正确性,且能够显著提高数控机床基础大件的精度保持性。

4 结 论

(1)通过对某卧式加工中心的床身部分进行应变监测,得到床身随时间的变形关系,并通过建立的几何误差模型得到床身变形和工作台面与地基理想平面平行度误差的传递关系。试验结果表明:该卧式加工中心床身在3个月内的变形是导致其工作台面与地基理想平面的平行度误差变化的主要原因,而振动时效效果不佳是导致床身精度保持性差的主要原因。

(2)提出一种振动时效工艺参数合理选择方法以及应力消除评价方法。选取了两个刚铸造完成、结构相同的床身进行了本文振动时效工艺和原振动时效工艺的效果比较,结果表明:振动时效本文工艺的平均应力消除率是65.1%,原工艺为38.5%(测试点4应力增加),本文工艺的平均应力消除率为原工艺的1.69倍,验证了新的振动时效工艺参数选择方法的正确性,且能够显著提高数控机床基础大件的精度保持性。

[1] 米谷茂.残余应力的产生及对策 [M].北京: 机械工业出版社,1983: 213-217.

[2] FERREIRA P M,LIU C R.An analytical quadratic

model for the geometric error of a machine tool [J].Journal of Manufacturing Systems,1986,5(1): 51-63.

[3] SATA T,TAKEUCHI Y,OKUBO N.Improvement of working accuracy of a machining center by computer control compensation [C]∥Proceedings of the 17th International Machine Tool Design and Research Conference.London,UK: Macmillan,1976: 93-99.

[4] NI J.CNC machine accuracy enhancement through real-time error compensation [J].J Manuf Sci Eng,1997,119(4B): 717-725.

[5] YUAN J,NI J.The real-time error compensation technique for CNC machining systems [J].Mechatronics,1998,8(4): 359-380.

[6] MUNSI A S M Y,WADDEL A J,WALKER C A.The influence of vibratory treatment on the fatigue life of welds: a comparison with thermal stress relief [J].Strain,2001,37(4): 141-149.

[7] 汤小牛,刘久明,张勇,等.JB/′I′5926-2005振动时效效果评定方法 [S].北京: 中华人民共和国国家发展和改革委员会,2005: 2-3.

[8] 廖凯,吴运新,龚海,等.积分法在铝合金厚板残余应力计算中的应用 [J].中国有色金属学报,2009,19(6): 1006-1011.

LIAO Kai,WU Yunxin,GONG Hai,et al.Application of integral method on residual stress calculation along depth in aluminium alloy thick plate [J].The Chinese Journal of Nonferrous Metals,2009,19(6): 1006-1011.

[9] LI Chunmei,CUI Fengkui.Research on VSR process for large machine tool body [J].Applied Mechanics and Materials,2011,44(1): 349-354.

[10]顾唯明.用钻孔应变测量决定残余应力的标准方法 [J].机械强度,1986,8(1): 40-43.

[11]潘光东,王文洁,董志鹏.HT250材料应力释放系数值的确定 [J].现代铸铁.2009(1): 87-89.

PAN Guangdong,WANG Wenjie,DONG Zhipeng.Determination of stress releasing factor of HT250grade gray iron [J].Modern Cast Iron,2009(1): 87-89.

[12]CLAXTON R A,LUPTON A.Vibratory stress relieving of welded fabrications [J].Welding & Metal Fabrication,1991,59(10): 541-542.

(编辑 杜秀杰)

AccuracyStabilityforLargeMachineToolBody

HU Min1,YU Changwu1,ZHANG Jun1,ZHAO Wanhua1,CUN Huaying2,YUAN Shengwan2

(1.State Key Laboratory for Manufacturing System Engineering,Xi’an Jiaotong University,Xi’an 710049,China;2.Shenji Group,Kunming Machine Tool Company Limited,Kunming 650203,China)

In view of the poor accuracy stability of the domestic large machine tool body due to the lack of standardization of vibration stress relief (VSR) process,a new method for achieving the best process parameters of VSR is proposed,Following the modal simulation and harmonic response analysis,on the same casting bed,the average stress elimination rate of the new process and the original process is comparatively evaluated.The average stress elimination rate of the new technology approaches 65.1% while that of the original process gets 38.5%,and the stress relieving rate of the bed in the new process reaches 1.69 times of that in the original process.

large machine tool body; accuracy stability; geometrical error model; vibration stress relief; blind hole method; stress relieving rate

2013-12-16。

胡敏(1986—),男,博士生;赵万华(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51235009);国家科技重大专项资助项目(2012ZX04012-031)。

时间:2014-03-06

10.7652/xjtuxb201406012

TH16

:A

:0253-987X(2014)06-0065-09

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140306.1435.005.html